↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Persistent homology (PH), a topological data analysis technique, offers a powerful way to understand the shape and structure of data. However, integrating PH into graph neural networks (GNNs) has been challenging due to marginal improvements with low interpretability. This research highlights the problem of using PH in GNNs in current approaches, emphasizing the need for a more effective integration method.
This paper introduces Topology-Invariant Pooling (TIP), a novel mechanism that aligns PH with graph pooling operations. TIP injects global topological invariance into pooling layers using PH, improving performance consistently. Experiments demonstrate that TIP significantly boosts the performance of several graph pooling methods across multiple datasets. The success is supported by the observed monotone relationship between pooling ratio and the proportion of non-zero persistence in PH, showcasing the alignment between PH and graph pooling. The method’s flexibility and consistent performance enhancements highlight its potential as a valuable tool for advancing graph neural network research.
Key Takeaways#
Why does it matter?#
This paper is important because it proposes a novel mechanism for integrating persistent homology (PH) into graph pooling methods in graph neural networks (GNNs). This addresses a critical limitation in current approaches, leading to improved performance and interpretability across various graph datasets. The findings open new avenues for research in topological data analysis and GNNs, potentially impacting various applications where graph-structured data is involved.
Visual Insights#

This figure illustrates the similarities between graph pooling (GP) and persistent homology (PH). Panel (a) shows how both methods hierarchically coarsen a graph, reducing it to a more compact representation. Panel (b) presents a graph showing the stable relationship between pooling ratio and the persistence ratio (percentage of non-zero persistence values in persistent homology). This relationship motivates the integration of PH into GP. Finally, Panel (c) depicts a persistence diagram, a common visualization tool used in persistent homology to represent topological features.
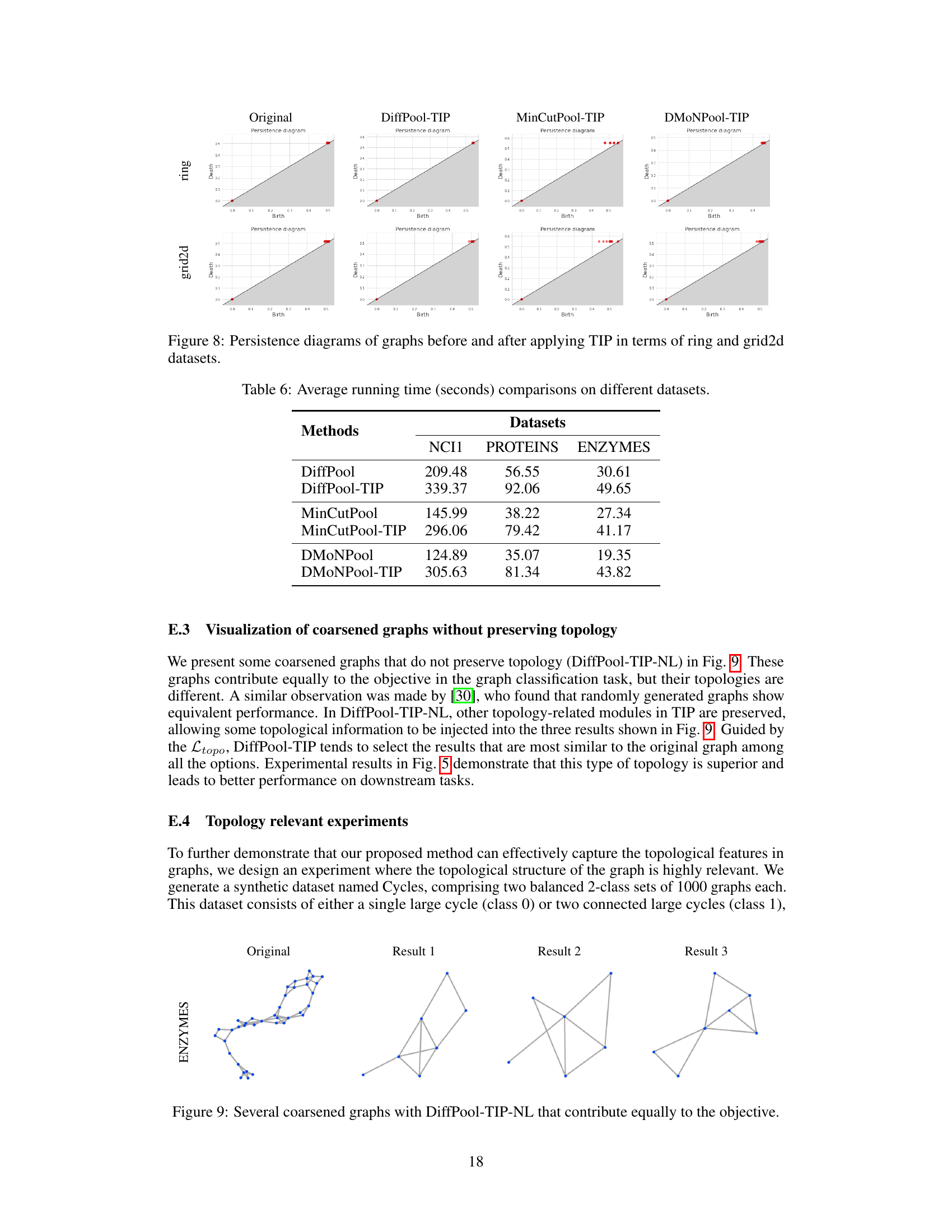
This table presents the Wasserstein distance, a metric measuring the topological similarity between the original and the coarsened graphs, for three different graph datasets (ring, torus, and grid2d) and several graph pooling methods. Lower values indicate higher similarity. The table aims to demonstrate the effectiveness of the Topology-Invariant Pooling (TIP) method in preserving topological structures during the graph pooling process.
In-depth insights#
Topological Pooling#
Topological pooling is a novel approach that integrates topological data analysis (specifically persistent homology) with graph pooling methods to enhance the performance of graph neural networks. The core idea is to leverage the hierarchical nature of persistent homology, which constructs a sequence of simplicial complexes from a point cloud or graph, to guide the pooling process. This allows the pooling operation to better preserve relevant topological information, leading to improved feature representation and classification accuracy. The alignment of persistent homology filtrations with the graph pooling cut-off offers a natural mechanism for injecting global topological invariance. Unlike traditional pooling methods that may discard crucial information, topological pooling aims to preserve persistent topological structures, which represent the most salient features of the data. This approach demonstrates improved performance compared to standard graph pooling methods across several datasets, suggesting its potential for widespread applicability and its ability to boost the expressive power of graph neural networks in various applications.
PH-GP Synergy#
The concept of ‘PH-GP Synergy’ explores the powerful combination of persistent homology (PH) and graph pooling (GP) in topological data analysis. PH provides a robust way to extract persistent topological features, offering a multi-resolution perspective on data structure. GP, on the other hand, effectively reduces the complexity of large graphs, making them more manageable for machine learning tasks. The synergy arises from the inherent alignment of these two techniques: PH’s hierarchical filtration process naturally mirrors GP’s progressive coarsening of a graph. By integrating PH features into GP layers, we obtain a more informative and topologically aware pooling operation. This approach not only improves the performance of existing GP methods but also enhances the interpretability of results. The key is to leverage PH’s ability to identify meaningful topological patterns, which are preserved as much as possible during the pooling process, ultimately resulting in better downstream task performance. This fusion unlocks new possibilities in topological data analysis and graph machine learning, offering a more powerful and insightful framework for analyzing complex data.
TIP’s Expressiveness#
The expressiveness of Topology-Invariant Pooling (TIP) hinges on its ability to capture and leverage topological information, going beyond the limitations of traditional graph pooling methods. TIP’s integration of persistent homology (PH) allows it to discern persistent topological features, which are invariant under certain graph transformations. This contrasts with methods solely reliant on local graph structures, making TIP robust to variations in node arrangement while still retaining crucial global topological information. The use of learnable filtration functions allows TIP to adapt to the specific characteristics of different datasets, further enhancing its expressiveness. Importantly, TIP’s design enables it to inject PH information at both the feature and topology levels, leading to a more comprehensive understanding of the graph structure. This multifaceted approach gives TIP a powerful expressive capacity, superior to methods that only utilize topological features at a superficial level or entirely ignore topological aspects.
TIP’s Limitations#
The Topology-Invariant Pooling (TIP) method, while showing promise in boosting graph pooling performance by integrating persistent homology, has inherent limitations. TIP’s reliance on circular structures might hinder its effectiveness on graphs with predominantly tree-like topologies, limiting its general applicability. The method’s performance is also sensitive to the choice of filtration function, and the impact of different filtrations on the results needs further investigation. While TIP effectively injects topological information, its success depends on the coarsened graph retaining essential sub-topologies, a condition not always guaranteed. The computational complexity, although manageable in many cases, could become a bottleneck for extremely large graphs. The proposed topological loss function, although effective, is an approximation and might not capture all nuances of topological similarity. Finally, the method’s generalizability across diverse datasets requires more thorough investigation; currently, there is a potential bias towards datasets with salient cyclical structures. Addressing these limitations would strengthen the robustness and wide applicability of the proposed method.
Future of TIP#
The future of Topology-Invariant Pooling (TIP) is promising, given its demonstrated ability to boost graph pooling performance by effectively integrating persistent homology. Future work could explore extensions to handle dynamic graphs, which would significantly broaden its applicability to real-world scenarios involving evolving relationships. Furthermore, investigating the impact of different filtration functions on TIP’s performance and interpretability would offer valuable insights into its underlying mechanics. Developing more efficient algorithms for computing persistent homology, crucial for scalability, remains important. Finally, exploring the potential of TIP in combination with other advanced graph neural network architectures and techniques, could lead to even more powerful graph learning models. A key area of research will focus on the theoretical analysis of TIP’s expressive power, particularly in its ability to capture and leverage complex topological features often missed by conventional methods. This deeper understanding would not only enhance its effectiveness but also contribute to the broader advancement of topological data analysis within machine learning.
More visual insights#
More on figures
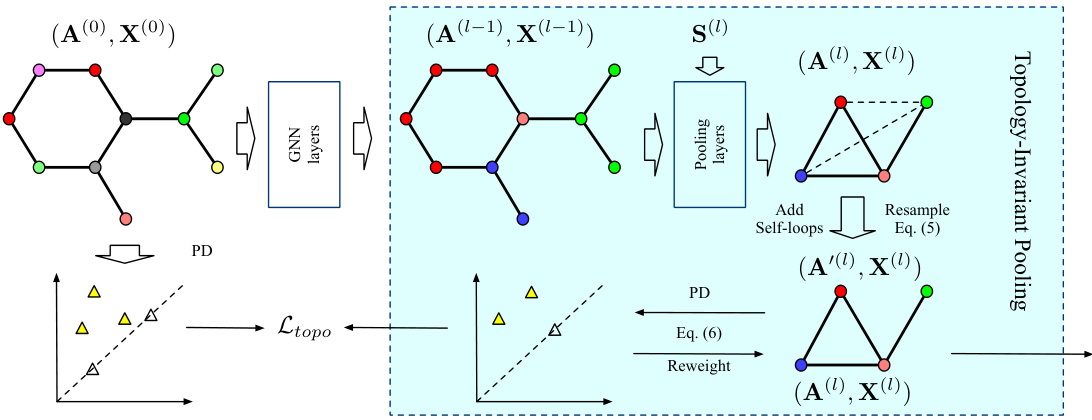
This figure illustrates the proposed Topology-Invariant Pooling (TIP) method. The process begins with an input graph represented by its adjacency matrix A(0) and node features X(0). Standard graph neural network (GNN) layers process the graph before it is passed to a graph pooling layer. The pooling layer generates a coarsened graph, represented by A(l-1) and X(l-1). This coarsened graph undergoes several steps: self-loops are added, a resampling process based on Equation (5) is applied to generate A’(l), and persistent homology is calculated to produce a persistence diagram (PD). Based on Equation (6), a reweighting process takes place, integrating topological information into A(l), thus obtaining (A(l), X(l)). The topological loss function Ltopo compares the original graph’s persistence diagram to the coarsened graph’s, guiding the topology-preserving process. The entire shaded block represents a single layer of the TIP method, which can be stacked for hierarchical pooling.

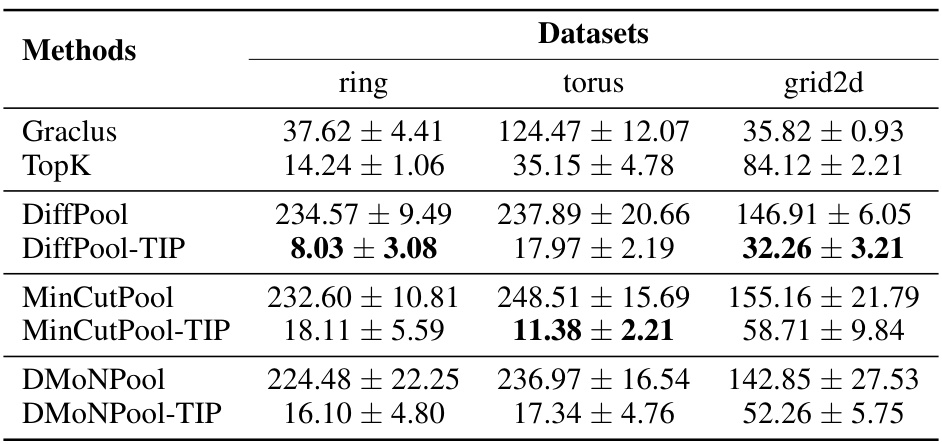
This figure visualizes the coarsened graphs obtained using different graph pooling methods (DiffPool, DiffPool-TIP, MinCutPool, MinCutPool-TIP, DMoNPool, DMoNPool-TIP, TopK, and Graclus) on three datasets (ring, torus, and grid2d). The goal is to show how well each method preserves the topological structure during the pooling process. The original graphs are shown in the leftmost column for comparison. TIP, which integrates persistent homology into the pooling methods, generally preserves more of the topological structure than the other methods, especially for ring and torus datasets. Dense pooling methods (DiffPool, MinCutPool, and DMoNPool) often produce dense graphs with little topological similarity to the original. Sparse methods (TopK and Graclus) also preserve less structure than TIP.
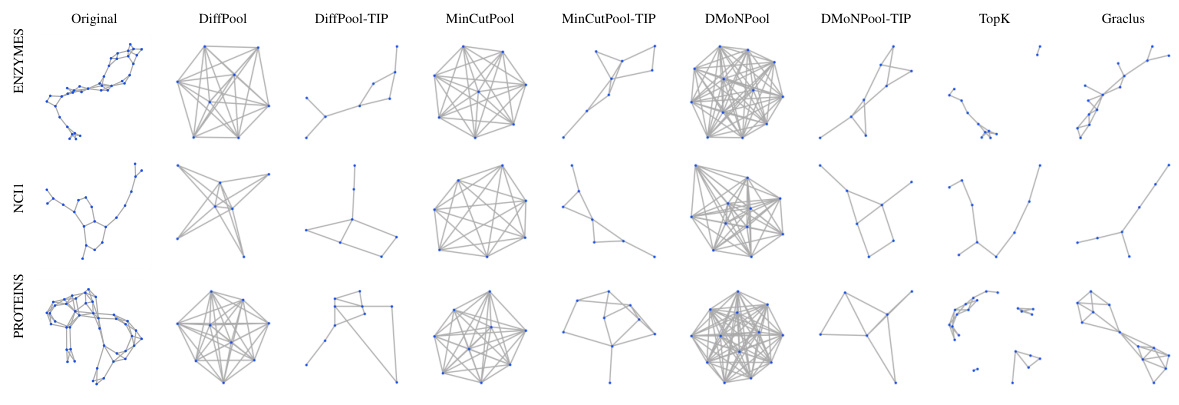
This figure compares the coarsened graphs generated by different graph pooling methods (DiffPool, DiffPool-TIP, MinCutPool, MinCutPool-TIP, DMoNPool, DMoNPool-TIP, TopK, and Graclus) on three different datasets (ring, torus, and grid2d). It visually demonstrates how well each method preserves the topological structure of the original graph after pooling. The goal is to show that TIP (Topology-Invariant Pooling) better maintains the original topology compared to other methods.
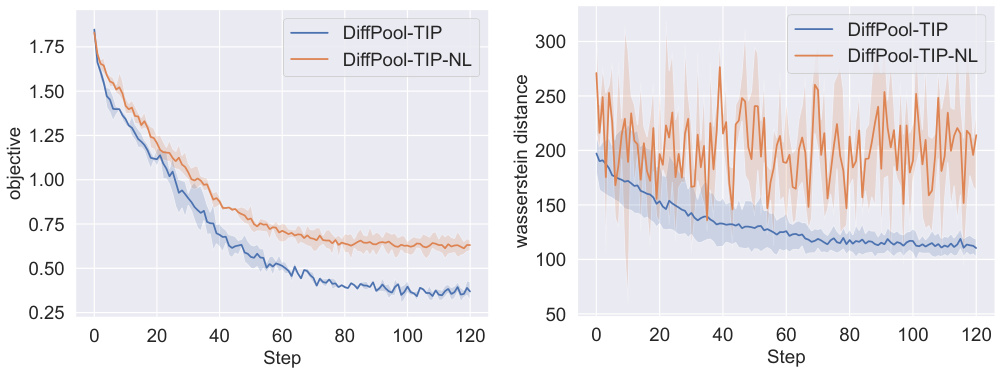
This figure displays the training curves for two different versions of the DiffPool graph pooling method: one with the proposed Topology-Invariant Pooling (TIP) and one without. It shows the objective function value and the Wasserstein distance between the persistence diagrams of the original and pooled graphs across multiple training steps (epochs). The Wasserstein distance measures the topological similarity. The plots illustrate that the TIP version converges to a lower objective value and maintains topological consistency better than the version without TIP.
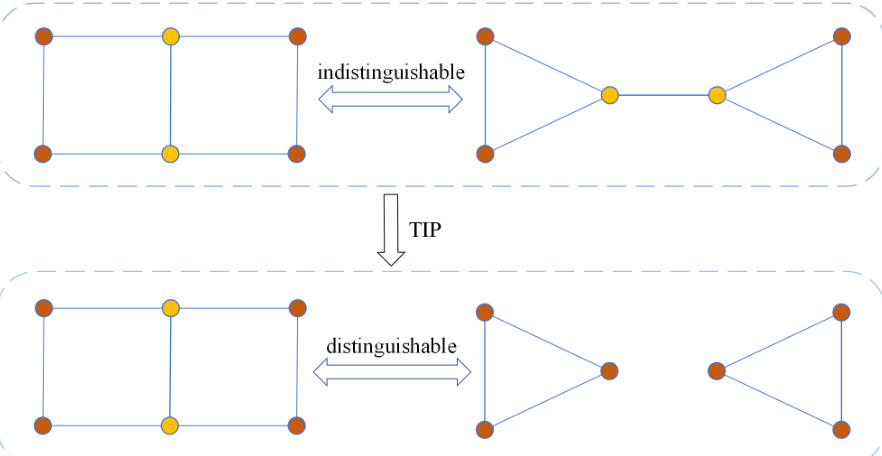
This figure shows two graphs that are indistinguishable by the 1-WL test (Weisfeiler-Lehman Isomorphism test), a common method for checking graph isomorphism. However, the TIP method (Topology-Invariant Pooling) can distinguish them. This highlights the enhanced expressive power of TIP compared to traditional methods for graph isomorphism.

This figure compares the coarsened graphs generated by different graph pooling methods in an experiment designed to evaluate their ability to preserve topological structure. The methods compared are DiffPool, DiffPool with TIP (Topology-Invariant Pooling), MinCutPool, MinCutPool with TIP, DMONPool, DMONPool with TIP, TopK, and Graclus. The visualization shows how effectively each method maintains the original graph’s topological features during the pooling process. The results indicate that methods incorporating TIP generally preserve more of the original topological structure compared to their counterparts without TIP.
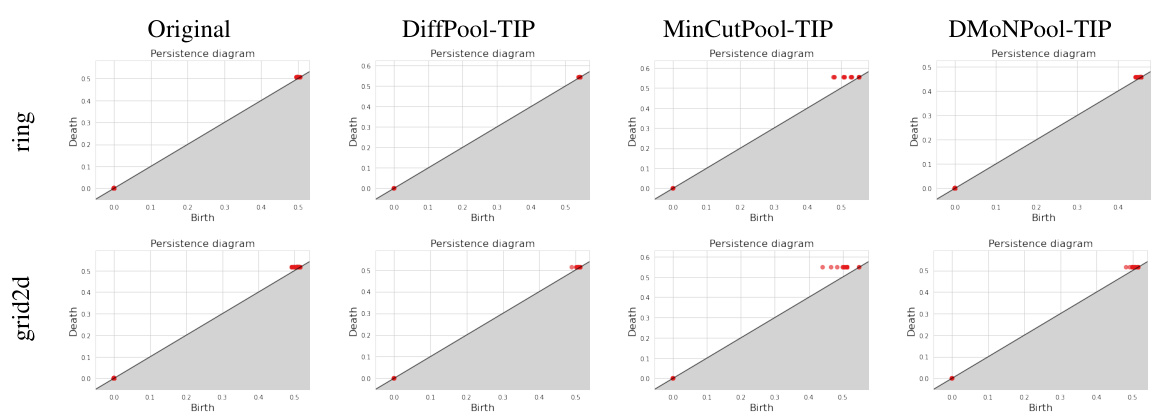
This figure visualizes persistence diagrams (PDs) for ring and grid2d graphs before and after applying Topology-Invariant Pooling (TIP). The diagrams illustrate the distribution of topological features (birth and death values) represented as points. Comparing the ‘Original’ PDs to those generated after TIP processing by DiffPool, MinCutPool, and DMoNPool, the visualization helps to assess the effect of TIP on preserving topological information during graph pooling. The preservation of key topological features after TIP indicates that TIP effectively preserves topological characteristics in the pooled graphs.

This figure visualizes the coarsened graphs produced by different graph pooling methods (DiffPool, DiffPool-TIP, MinCutPool, MinCutPool-TIP, DMONPool, DMONPool-TIP, TopK, Graclus) on three datasets: ring, torus, and grid2d. It demonstrates how different methods handle the preservation of topological structures during the pooling process. The original graphs are shown for comparison, highlighting how TIP (Topology-Invariant Pooling) generally preserves the topological structures better than the other methods.
More on tables

This table presents the test accuracy results for graph classification on several benchmark datasets. The methods compared include various GNN models (GCN, GIN, GraphSAGE, TOGL, GSN), sparse pooling methods (Graclus, TopK), and dense pooling methods (DiffPool, MinCutPool, DMoNPool), both with and without the proposed TIP enhancement. The table shows the mean test accuracy and standard deviation across multiple runs for each method and dataset. A bold value highlights the best-performing method for each dataset, and gray shading indicates datasets where the TIP-enhanced version outperformed the base pooling method.

This table presents the mean and standard deviation of prediction accuracy for the constrained solubility of molecules in the ZINC dataset, using mean square error as the performance metric. It shows the results for three different graph pooling methods (DiffPool, MinCutPool, and DMoNPool) both with and without the TIP enhancement. The lower the mean square error, the better the performance.

This table shows the unsupervised loss functions used in three different dense graph pooling methods: DiffPool, MinCutPool, and DMoNPool. For each method, it lists the reconstruction loss (Lr) and the clustering loss (Lc). The reconstruction loss aims to reconstruct the original graph from the pooled graph, while the clustering loss encourages good clustering quality. The specific formulas for these losses are given using matrix notation. Understanding this table helps to grasp the differences in how the different pooling methods approach the task of coarsening a graph while preserving important structural information.

This table presents the key statistics of the various datasets used in the paper’s experiments. For each dataset, it lists the number of graphs, the average number of nodes per graph, the average number of edges per graph, the number of features associated with each node, and the number of classes or labels present in the dataset.

This table presents the average running time in seconds for different graph pooling methods (DiffPool, DiffPool-TIP, MinCutPool, MinCutPool-TIP, DMONPool, DMONPool-TIP) across three benchmark datasets (NCI1, PROTEINS, ENZYMES). The running time reflects the computational cost of each method, providing insights into their efficiency. The inclusion of TIP (Topology-Invariant Pooling) generally increases the runtime, indicating the additional computational requirements associated with incorporating persistent homology.
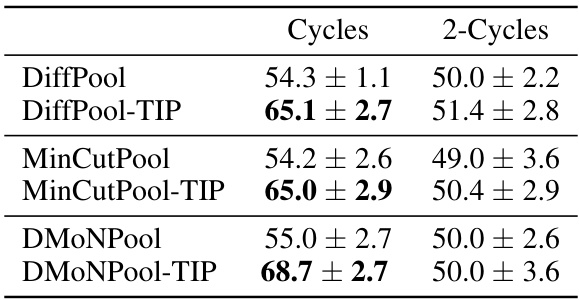
This table presents the classification accuracy results on two synthetic datasets: ‘Cycles’ and ‘2-Cycles’. Each dataset consists of 1000 graphs, divided into two classes based on topological features (presence or absence of cycles, or number of connected components). The table shows the performance of different graph pooling methods (DiffPool, MinCutPool, and DMoNPool) with and without the proposed TIP method. The results demonstrate the effectiveness of TIP in improving classification accuracy, particularly for graphs with certain topological structures.

This table presents the results of ablation studies performed on four datasets (NCI1, PROTEINS, ENZYMES, IMDB-BINARY) to assess the impact of each module (resampling, persistence injection, topological loss, 0-dimensional topological features, fixed filtration) within the TIP model on the graph classification task. For each dataset and each ablation variant, the test accuracy is reported with standard deviation. The table allows for a comparison of the performance of the complete TIP model against various versions with individual components removed, highlighting the importance of each component for overall performance.

This table presents the test accuracy results of three different graph pooling methods (DiffPool, MinCutPool, and DMoNPool) and their corresponding versions integrated with the proposed Topology-Invariant Pooling (TIP) method. The EXPWL1 dataset is used, which consists of graph pairs designed to test the expressive power of graph pooling methods in distinguishing non-isomorphic graphs. The results demonstrate that integrating TIP consistently improves the test accuracy of all three pooling methods, showcasing TIP’s effectiveness in enhancing the expressive power of graph pooling.
Full paper#