Aligning Diffusion Behaviors with Q-functions for Efficient Continuous Control

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap between offline reinforcement learning and large language model alignment, offering a novel and efficient approach for continuous control tasks. It addresses the limitations of existing methods by leveraging the power of diffusion models, improving data efficiency, and accelerating policy optimization. The findings provide a pathway for applying LLM alignment techniques to offline RL in various applications, including robotics and AI safety.

Visual Insights

#

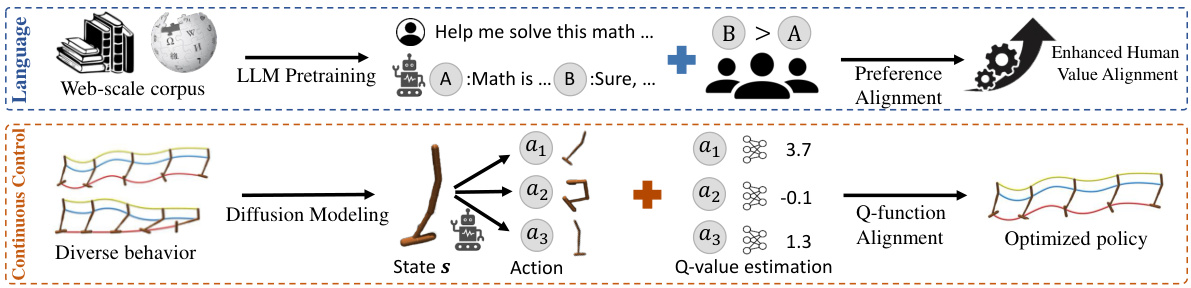
This figure illustrates the similarities between the alignment strategies used for Large Language Models (LLMs) and diffusion policies in continuous control tasks. The top half shows the LLM alignment process, where a pre-trained LLM is fine-tuned using human preferences to align its outputs with desired behavior. The bottom half shows the analogous process for diffusion policies, where a pre-trained diffusion model representing diverse behaviors is fine-tuned using Q-values to produce optimized policies for control tasks. The figure highlights the parallel steps of pretraining, alignment with human feedback (preferences for LLMs, Q-functions for diffusion models), and the resulting enhancement of the model to reflect human intentions or optimal policy.

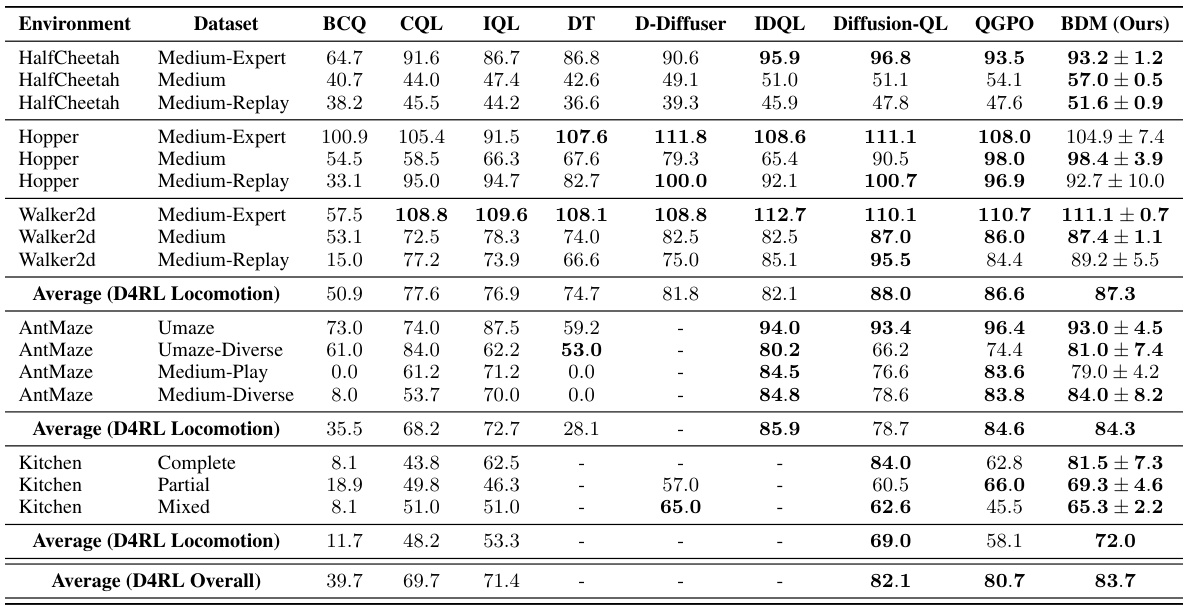
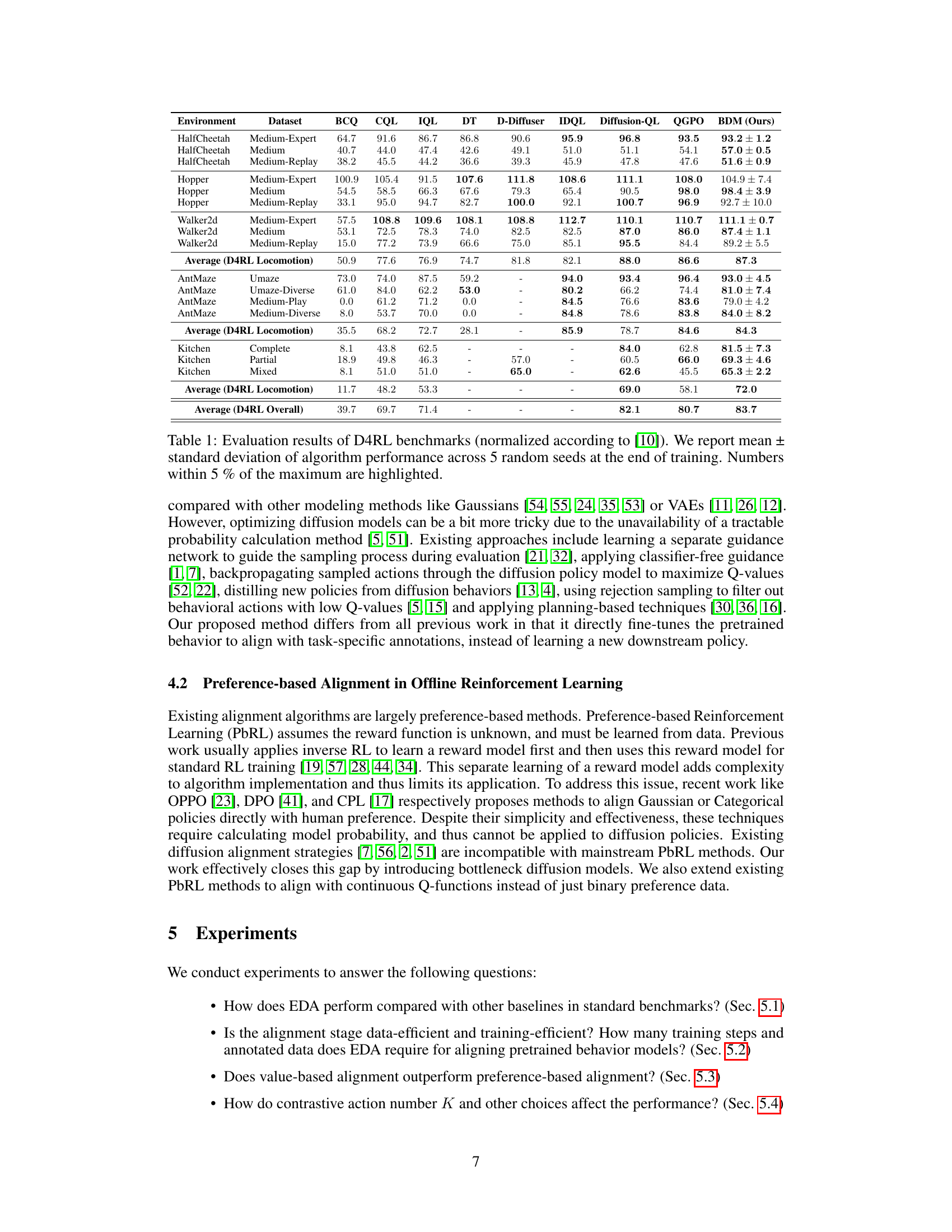
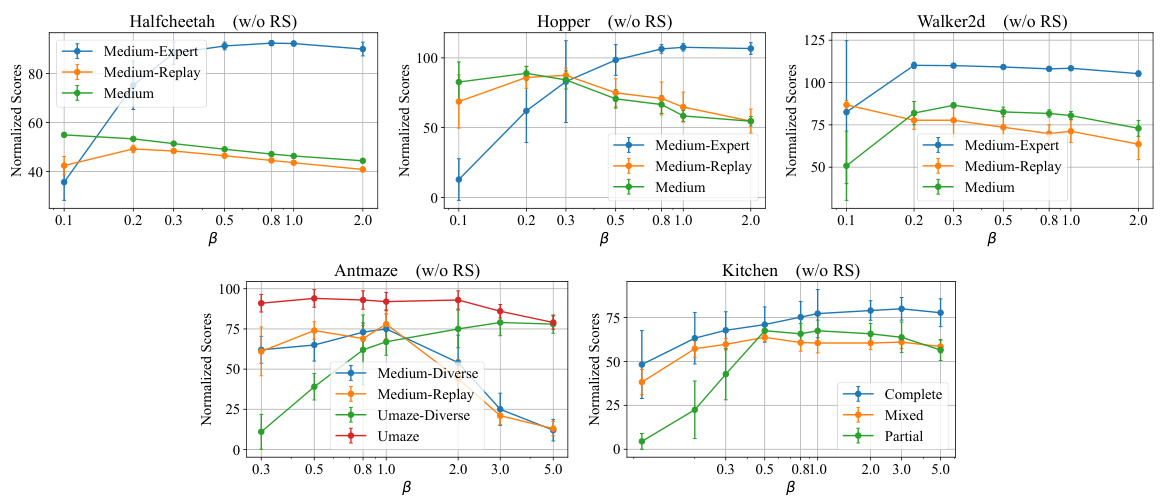
This table presents the results of the D4RL benchmark experiments, comparing the performance of the proposed EDA method against several baselines. The table shows the average normalized scores across five random seeds for each algorithm on various D4RL tasks, categorized by environment and dataset difficulty (e.g., HalfCheetah Medium-Expert, Hopper Medium-Replay). Scores within 5% of the highest score for each task are highlighted. The results demonstrate the superior performance of EDA compared to other approaches.

In-depth insights

#

Offline RL Alignment

#

Offline reinforcement learning (RL) alignment presents a unique challenge: how to effectively leverage large, pre-collected datasets to train performant policies without the need for extensive online interaction. The core issue lies in the suboptimality often present in offline datasets, reflecting the behavior of imperfect policies. Simply training a new policy directly on this data often leads to poor generalization. Alignment techniques aim to address this by incorporating additional information or constraints during training. This might involve using reward functions, expert demonstrations, or preference labels to guide the policy toward improved performance. A crucial aspect is choosing an appropriate representation for the policies themselves, which can significantly impact the effectiveness and efficiency of the alignment process. The choice between using parametric models, such as neural networks, or non-parametric approaches impacts the ability to model complex behaviors and to efficiently integrate additional information for alignment. Successful alignment strategies often balance the expressiveness of the policy representation with the ability to effectively incorporate the available offline data and any additional signals (such as rewards or preferences). The ultimate goal is to obtain policies that generalize well to unseen situations and exhibit superior performance compared to policies trained solely on the offline data without alignment guidance.

Diffusion Policy

#

Diffusion models, known for their proficiency in generating diverse samples, have recently emerged as powerful tools for representing complex behavior in reinforcement learning. A diffusion policy leverages this capability by modeling the probability distribution of actions, effectively capturing nuanced and multimodal behaviors often unseen in simpler policy representations. This approach allows for greater expressiveness, enabling the learning of more sophisticated and adaptable policies. The key challenge lies in translating the generative capabilities of diffusion models into efficient optimization methods for reinforcement learning. Unlike traditional policies based on explicit parameterizations, diffusion policies present a unique optimization landscape. Their probability density estimation often relies on intricate score functions, demanding novel techniques for efficiently fine-tuning or aligning these policies to reward signals. This optimization challenge often necessitates the incorporation of advanced alignment methodologies, sometimes borrowing from approaches used for large language models. While this can yield highly effective policies, it also brings the complexity of dealing with intricate score function calculations and the need for efficient adaptation to specific tasks using minimal data. Research on efficient optimization and alignment of diffusion policies is ongoing, aiming for faster training and better data efficiency.

EDA Algorithm

#

The Efficient Diffusion Alignment (EDA) algorithm presents a novel approach to offline reinforcement learning, particularly focusing on continuous control tasks. EDA cleverly leverages the strengths of diffusion models for behavior modeling, but critically addresses the limitations of directly applying existing language model alignment techniques to this domain. This is achieved by representing diffusion policies as the derivative of a scalar neural network, enabling direct density calculations and compatibility with methods like Direct Preference Optimization (DPO). The two-stage process, pretraining a diffusion behavior model on reward-free data and then fine-tuning it with Q-function annotations, allows for efficient adaptation to downstream tasks using minimal labeled data. This data-efficiency is highlighted by EDA’s ability to retain a substantial amount of performance even with a very small percentage of Q-labeled data. The algorithm’s key innovation lies in its ability to directly align diffusion behaviors with continuous Q-functions, going beyond the binary preferences commonly used in language model alignment. This is accomplished through a novel training objective that frames the problem as a classification task, predicting the optimal action among multiple candidates. Overall, EDA demonstrates promising results in continuous control, showcasing its potential for data-efficient and rapid policy adaptation in various applications.

Data Efficiency

#

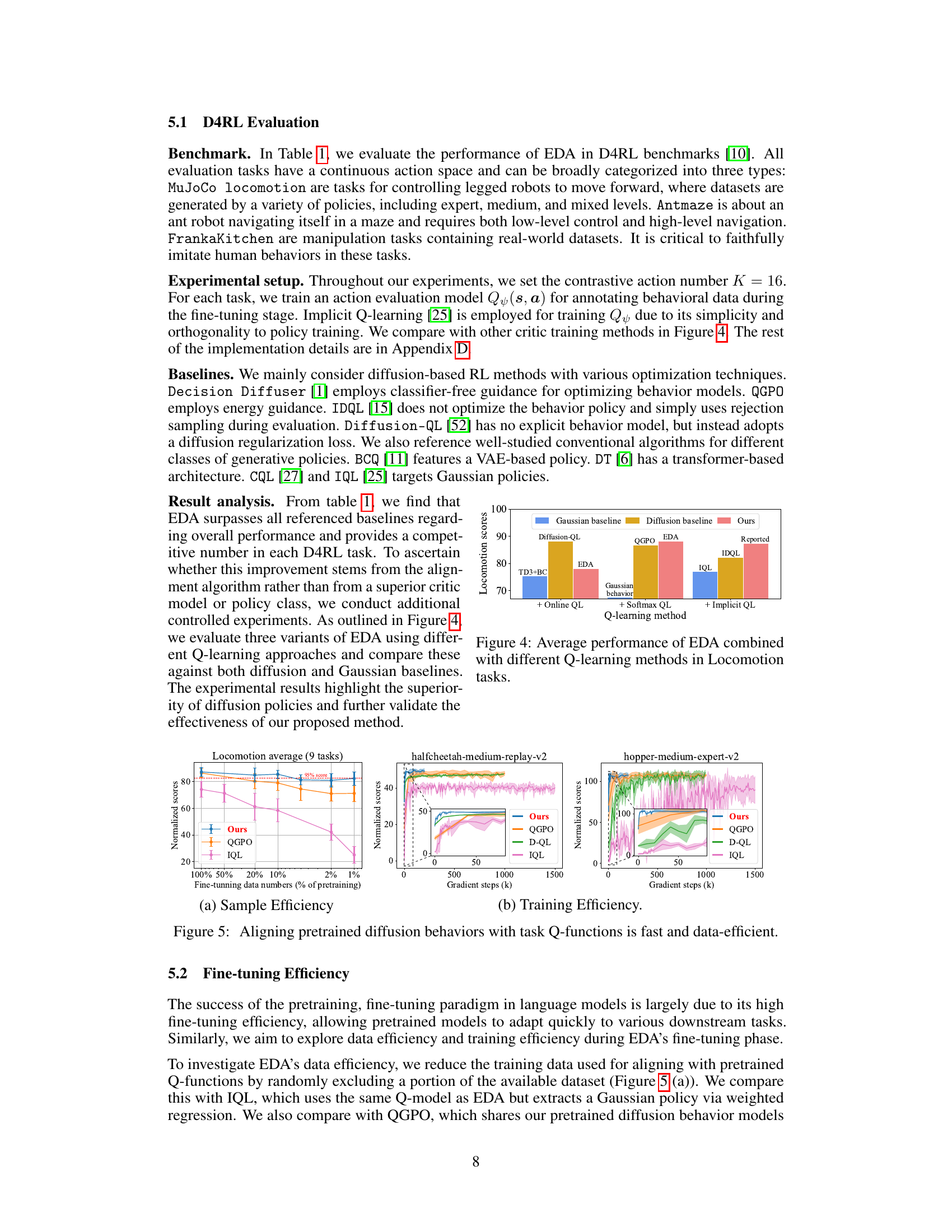
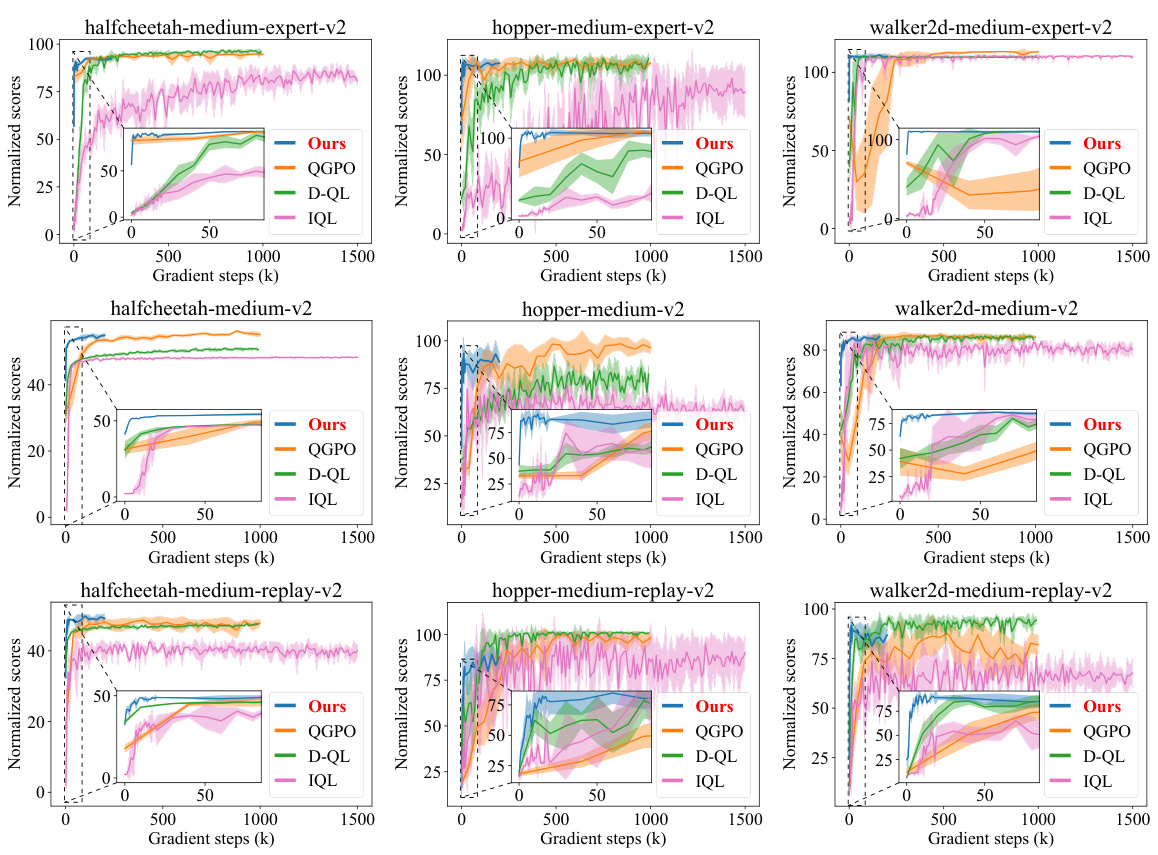
The research demonstrates impressive data efficiency, particularly during the policy fine-tuning stage. Using only 1% of the Q-labeled data compared to the pretraining phase, the model maintains approximately 95% of its performance and still surpasses various baselines. This highlights the efficacy of leveraging a large, diverse, reward-free dataset for pretraining, allowing the model to generalize well and adapt rapidly to downstream tasks with minimal additional annotation. The rapid convergence during fine-tuning, achieving satisfactory results with only about 20,000 gradient steps, further underscores the data efficiency of the proposed method. This efficiency is attributed to the model’s strong generalization ability acquired during pretraining, enabling efficient adaptation to new tasks with limited data. This characteristic is crucial for real-world applications where acquiring labeled data can be expensive and time-consuming. The results suggest a promising approach to scaling offline reinforcement learning methods, making them more practical for various domains.

Future Work

#

Future research directions stemming from this work could explore several promising avenues. Extending EDA to discrete action spaces is crucial for broader applicability, requiring new techniques to estimate density and adapt alignment methods. Investigating alternative policy representations beyond the derivative of a scalar network could unlock even greater flexibility and expressiveness. Furthermore, empirical evaluation across a wider range of continuous control tasks is warranted, especially in complex, real-world scenarios to validate the robustness and generalization capabilities of EDA. Developing more efficient Q-function estimation methods that require fewer annotations would significantly enhance data efficiency. Finally, a thorough theoretical investigation into the convergence properties and stability of EDA across diverse datasets and tasks would solidify its foundations and guide further improvements.

More visual insights

#

More on figures

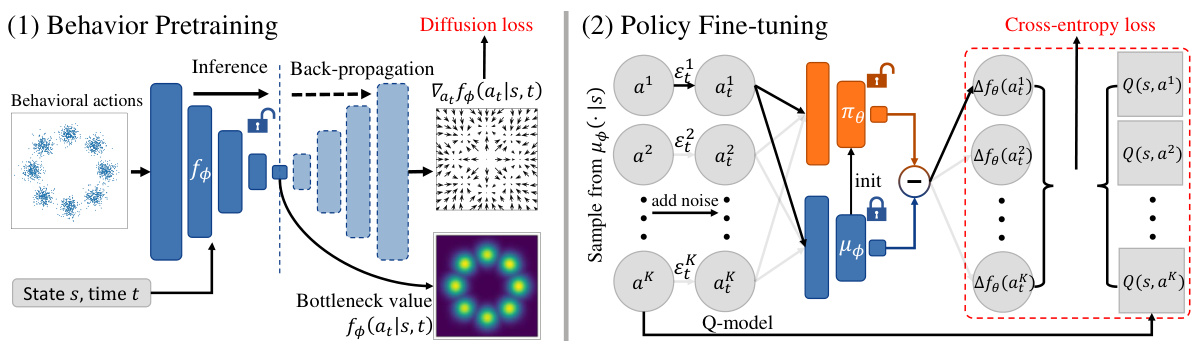
This figure illustrates the two-stage process of the Efficient Diffusion Alignment (EDA) algorithm. The left side shows the behavior pretraining stage, where a diffusion behavior model is represented as the derivative of a scalar neural network. This allows for direct density calculation, which is crucial for aligning diffusion behaviors with Q-functions. The right side depicts the policy fine-tuning stage, where the algorithm predicts the optimality of actions contrastively using a cross-entropy loss function. The goal is to align the pretrained diffusion behavior with the provided Q-function values, improving the policy’s performance.

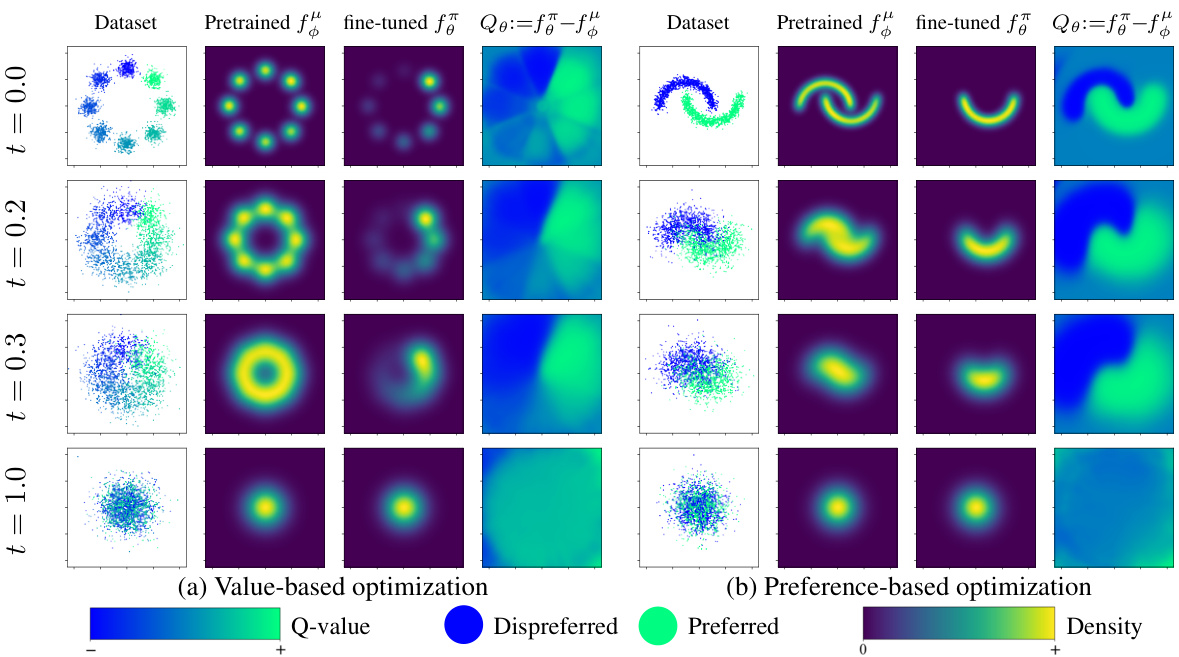
This figure shows the results of the Efficient Diffusion Alignment (EDA) algorithm on 2D bandit tasks. The left side demonstrates value-based optimization, while the right side shows preference-based optimization. Each column represents different aspects: the dataset, pretrained model, fine-tuned model, and predicted Q-values. The results illustrate EDA’s ability to effectively decrease the density of low-Q-value actions after fine-tuning, aligning the predicted Q-values with the actual dataset values.

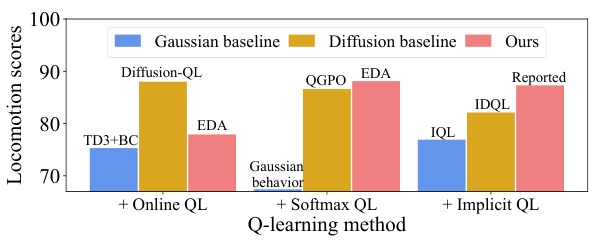
This figure compares the performance of EDA (Efficient Diffusion Alignment) combined with three different Q-learning methods (Online QL, Softmax QL, Implicit QL) against several baselines (Gaussian baseline, Diffusion baseline, Diffusion-QL, QGPO, IDQL, IQL, TD3+BC). The results are presented in terms of average locomotion scores across multiple tasks. The goal is to demonstrate the effect of the Q-learning method on EDA’s performance and to compare it against other approaches in continuous control tasks.

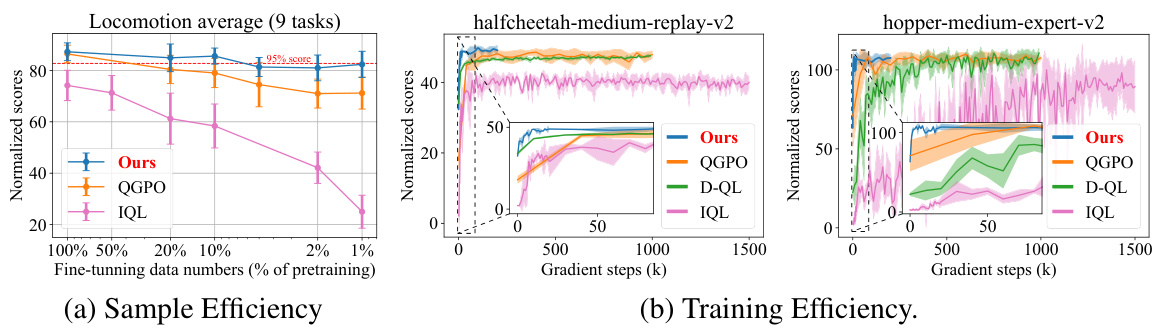
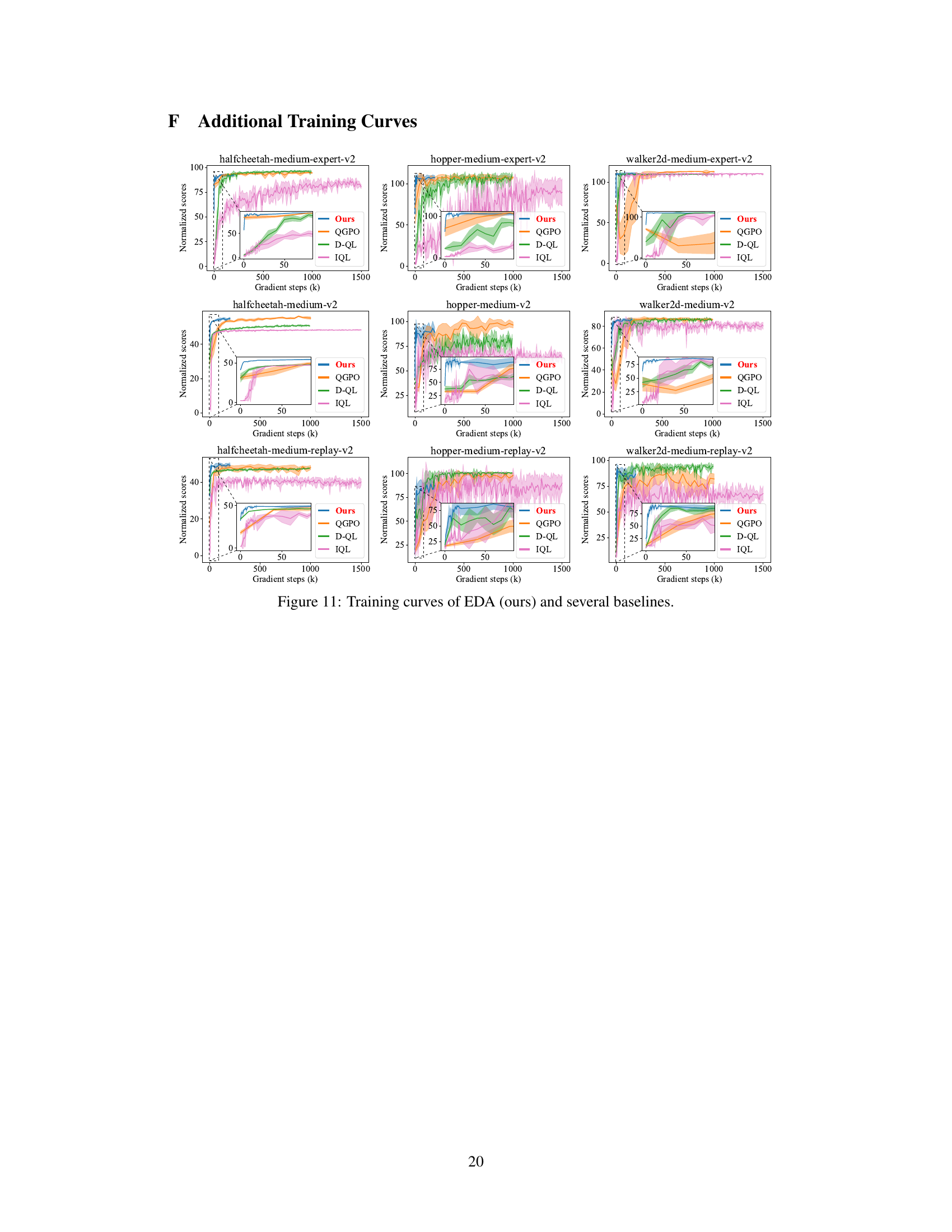
This figure shows the results of experiments on the data and training efficiency of the proposed method, EDA, for aligning pretrained diffusion behaviors with task Q-functions. Subfigure (a) demonstrates the sample efficiency by showing how EDA maintains high performance even with a small percentage of Q-labeled data during fine-tuning compared to other baselines. Subfigure (b) illustrates the training efficiency by plotting the normalized scores over gradient steps, highlighting that EDA converges quickly compared to other methods.

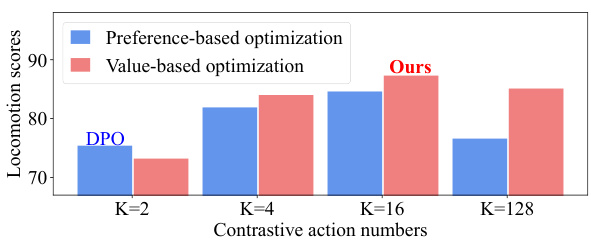
This figure shows the ablation study on the number of contrastive actions (K) and the comparison between preference-based and value-based optimization methods. The results demonstrate that the value-based optimization method (EDA, ours) generally outperforms the preference-based optimization method (DPO). The performance gap widens as K increases, suggesting that value-based optimization is more robust to the number of action samples considered.

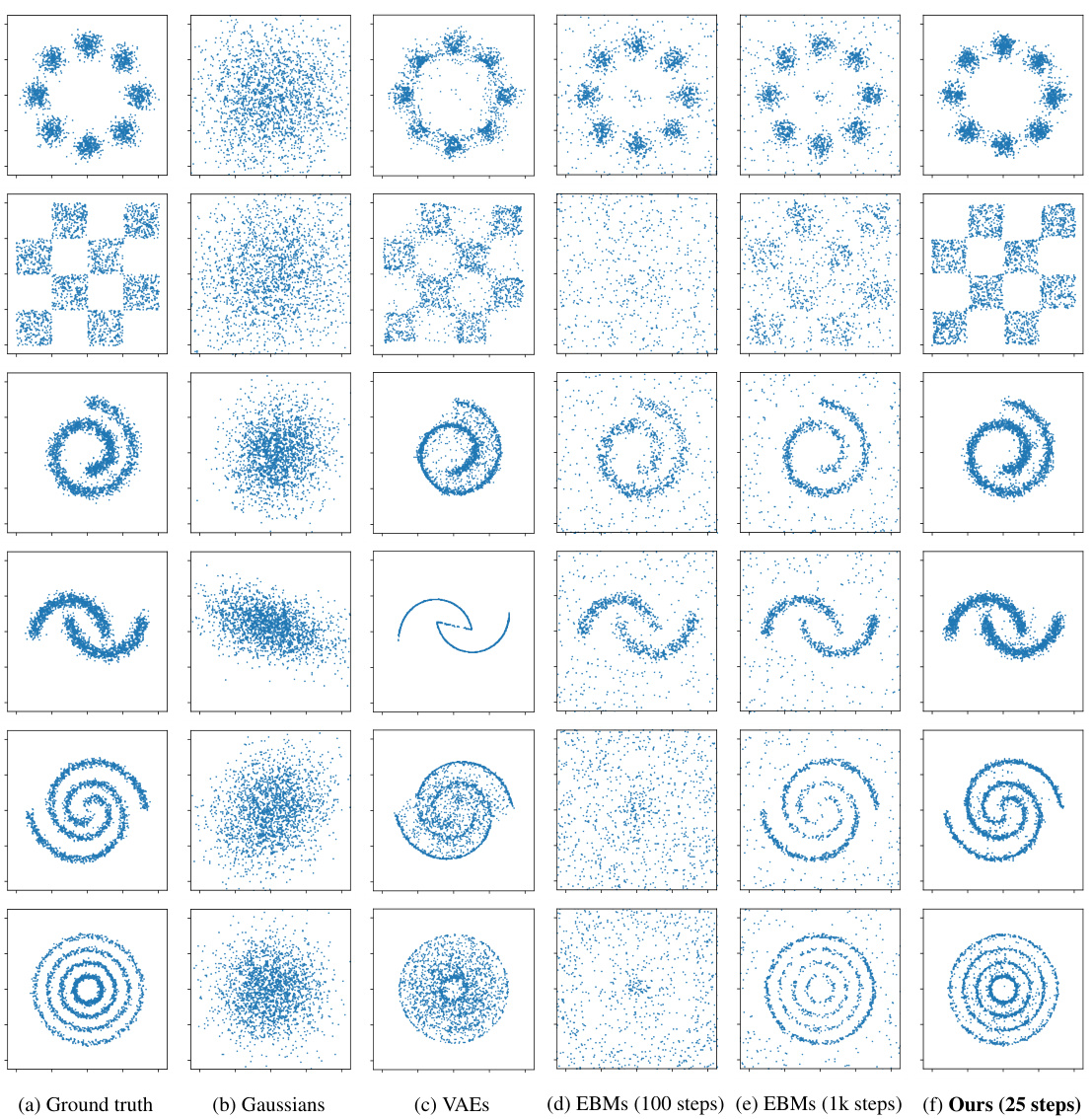
This figure compares the performance of various generative models (Ground truth, Gaussians, VAEs, EBMs with 100 and 1k steps, and the proposed Bottleneck Diffusion Models (BDMs) with 25 steps) in 2D modeling and sampling tasks. It visually demonstrates the efficiency and effectiveness of the proposed BDMs in generating high-quality samples that closely resemble the ground truth, especially when compared to other methods requiring substantially more steps for convergence.

This figure shows the results of the Efficient Diffusion Alignment (EDA) method applied to 2D bandit problems. It compares the performance of value-based and preference-based optimization strategies at different diffusion times. The visualization includes the behavior datasets, density maps estimated by BDM models (both pretrained and fine-tuned), and predicted action Q-values. The results demonstrate that EDA effectively reduces the density of low-Q-value actions after fine-tuning.

This figure shows the effectiveness of EDA in 2D bandit experiments at various diffusion times. It compares value-based and preference-based optimization methods, illustrating how the density of actions with low Q-values is reduced after fine-tuning the BDM model. The predicted Q-values from the model closely align with the actual Q-values in the dataset.

This figure shows the results of the Efficient Diffusion Alignment (EDA) method on 2D bandit tasks. It compares the behavior datasets, density maps, and predicted Q-values before and after fine-tuning. The results demonstrate that EDA effectively reduces the density of actions with low Q-values, aligning the learned policy with the desired behavior.

This figure shows the results of Efficient Diffusion Alignment (EDA) on 2D bandit tasks. It compares the behavior dataset, the density maps of the pretrained and fine-tuned bottleneck diffusion models (BDMs), and the predicted Q-values before and after fine-tuning. The visualization demonstrates EDA’s ability to effectively decrease the density of actions with low Q-values.

Full paper

#