↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current methods for studying the brain-muscle connection, like cortico-muscular coherence (CMC), have limitations in capturing complex, high-level relationships. This restricts our understanding of motor control and hinders the development of advanced diagnostic and therapeutic tools for neurological disorders. There’s a need for better statistical tools that can address these issues.
This research introduces a new approach called FMCA-T, which uses a technique called orthonormal decomposition of density ratios. This method analyzes EEG and EMG signals to reveal more detailed information about brain-muscle interactions, including channel-specific and time-dependent relationships. The key findings demonstrate that FMCA-T improves the accuracy of movement and subject classification and reveals important patterns in brain activity during movement. This advance has significant implications for both neuroscience research and the development of new clinical tools.
Key Takeaways#
Why does it matter?#
This paper is important because it presents a novel method for analyzing cortico-muscular connectivity, a crucial area in neuroscience with implications for understanding motor control and treating neurological disorders. The proposed method, Functional Maximal Correlation Algorithm with Trace Cost (FMCA-T), offers significant advantages over existing techniques by providing a more robust and scalable way to model the complex relationship between brain and muscle activity, allowing for better classification of movements and subjects. The findings also open new avenues for research on brain-computer interfaces and the development of more sophisticated diagnostic tools for neuromuscular disorders.
Visual Insights#
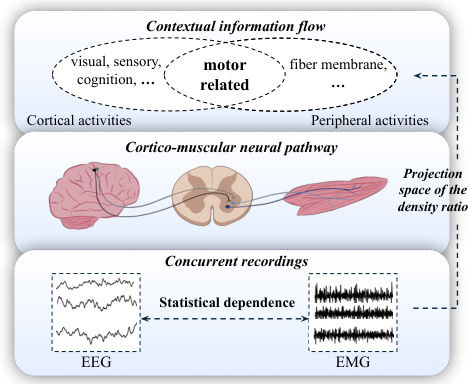
This figure illustrates the cortico-muscular neural pathway, showing how brain signals (EEG) and muscle signals (EMG) are connected. The pathway starts in the cortex, goes through the spinal cord, and reaches the muscles. The figure highlights that cortical oscillations are coherent with oscillations in muscle activities, which is critical in neuroscience and is the focus of study in the paper. Concurrent recordings of EEG and EMG are used to model the statistical dependence of this connectivity.
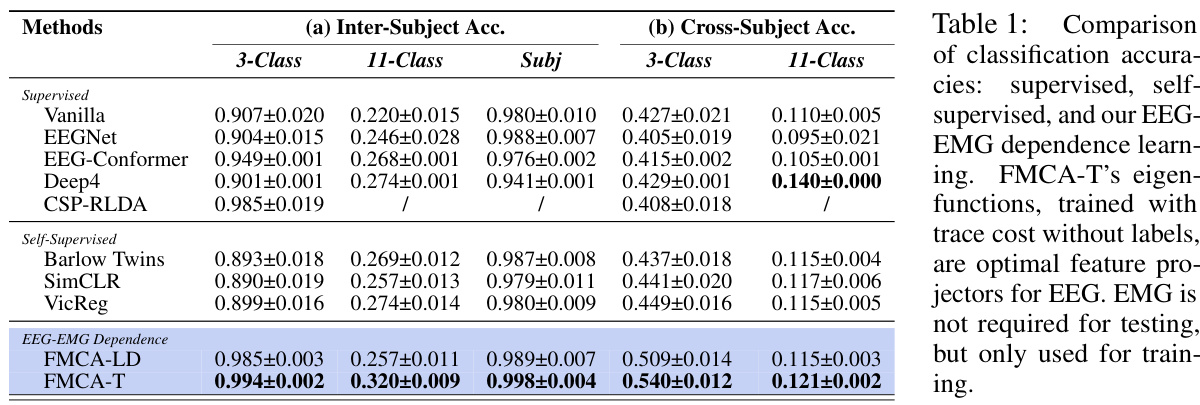
The table compares the classification accuracies of different methods on three classification tasks (3-class, 11-class, and subject classification). It includes supervised methods (Vanilla, EEGNet, EEG-Conformer, Deep4, CSP-RLDA), self-supervised methods (Barlow Twins, SimCLR, VicReg), and the proposed EEG-EMG dependence learning methods (FMCA-LD and FMCA-T). The results show that FMCA-T, using the trace cost, achieves the highest accuracy in most cases, demonstrating the effectiveness of using EEG eigenfunctions for classification without the need for EMG data during testing.
In-depth insights#
Cortico-Muscular Link#
The cortico-muscular link, the pathway by which the brain controls muscle movement, is a critical area of neuroscience research. This paper investigates this link by proposing a novel method using orthonormal decomposition of density ratios to model the complex relationship between electroencephalography (EEG) and electromyography (EMG) signals. This approach moves beyond traditional coherence measures by capturing higher-order statistical dependencies and providing a richer understanding of the spatiotemporal dynamics of this link. Eigenfunctions derived from this method are shown to effectively classify movements and individuals, suggesting they capture essential features of cortico-muscular communication. Further, analysis of these eigenfunctions reveals specific EEG channel and temporal dependencies, confirming the expected activation patterns during movement. This work demonstrates the potential of this novel approach for gaining valuable insight into the workings of the cortico-muscular link and its applications in diagnosing and monitoring neuromuscular disorders and brain-computer interface development. The robust performance against noisy data further supports its potential practicality in real-world applications.
Density Ratio Deconstruction#
Density ratio deconstruction, in the context of analyzing relationships between EEG and EMG signals, offers a powerful approach for understanding cortico-muscular coupling. The core idea revolves around representing the relationship between these signals not as a simple correlation, but as a ratio of their joint and marginal probability densities. This density ratio encapsulates the complexities of their interdependence beyond linear relationships, revealing nuanced interactions. Orthonormal decomposition of this density ratio further enhances interpretability, by transforming a complex relationship into a set of orthogonal components (eigenfunctions and eigenvalues). These components can then be analyzed to identify key features that explain the observed cortico-muscular relationship. Eigenfunctions capture contextual information, such as the specific movements being performed or even the individual subject, providing a powerful method for classification. Eigenvalues, on the other hand, quantify the strength of dependence, allowing for a multivariate assessment of the coupling. Therefore, the deconstruction method allows for the identification of both high-level, context-dependent associations and localized spatiotemporal dependencies within the EEG-EMG signals. This multi-faceted approach provides a superior understanding of the complex dynamics of cortico-muscular control compared to traditional scalar-based measures.
FMCA-T Algorithm#
The hypothetical ‘FMCA-T Algorithm’ likely centers on an improved version of the Functional Maximal Correlation Algorithm (FMCA), focusing on optimizing a matrix trace cost function rather than the traditional log determinant. This modification is crucial for enhanced computational efficiency and stability, particularly when dealing with high-dimensional data such as EEG and EMG signals. The algorithm likely involves iterative optimization of neural networks to learn the eigenvalues and eigenfunctions of the density ratio between EEG and EMG, providing a multivariate measure of dependence rather than a scalar value. The choice of a matrix trace cost function suggests a more direct approach to maximizing the sum of eigenvalues, unlike the log determinant which focuses on the product. The improved stability and scalability are significant advantages, especially given the challenges in analyzing the noisy, high-dimensional nature of neural recordings. The decomposition into eigenvalues and eigenfunctions provides not only a quantitative measure of dependence, but also allows for a deeper understanding by revealing the spatio-temporal dynamics of the cortico-muscular relationship through its eigenfunctions.
EEG Feature Extraction#
EEG feature extraction plays a crucial role in brain-computer interfaces (BCIs) and other neurotechnology applications. The goal is to transform raw EEG signals into a format suitable for machine learning algorithms or other analysis techniques. Effective feature extraction is vital for accurate and reliable performance, as poor feature selection can lead to inaccurate classifications or predictions. Common EEG features include time-domain features (e.g., mean, variance, standard deviation), frequency-domain features (e.g., power spectral density, frequency bands), and time-frequency features (e.g., wavelet transform, short-time Fourier transform). The choice of features depends on the specific application and the nature of the EEG data. Advanced techniques like independent component analysis (ICA) and principal component analysis (PCA) are often employed to reduce dimensionality and remove noise or artifacts. Furthermore, feature selection methods are used to identify the most relevant features for a given task, improving accuracy and efficiency. The selection of optimal features is a critical step that often involves experimentation and evaluation using various classification methods. Ultimately, successful EEG feature extraction relies on a careful consideration of the research question, the characteristics of the EEG data, and the computational demands of the chosen analysis methods.
Future Research#
Future research directions stemming from this work on cortico-muscular dependence using orthonormal decomposition of density ratios could explore several promising avenues. Extending the methodology to larger, more diverse datasets is crucial for confirming the generalizability of findings across populations and movement types. Incorporating additional bio-signal modalities, such as electrogastrography or force sensors, could provide a richer understanding of the interplay between neural activity, muscular activation, and overall movement execution. A significant advance would involve developing more sophisticated network architectures, such as transformers, to capture potentially more intricate spatio-temporal relationships within the data. Further investigation into the inherent robustness and limitations of the method in handling noisy or incomplete data would bolster its practical applicability. Finally, exploring the clinical potential of this technique for diagnosing and monitoring various neuromuscular disorders should be a high priority, and the effectiveness of using the learned eigenfunctions for regression tasks (e.g., predicting muscle forces or movement kinematics) warrants investigation.
More visual insights#
More on figures

This figure illustrates the proposed framework for learning cortico-muscular dependence through orthonormal decomposition of density ratios. It shows the network architecture, the process of approximating the density ratio, the feature projection space formed by EEG eigenfunctions, and how channel-level and temporal-level dependencies are analyzed.
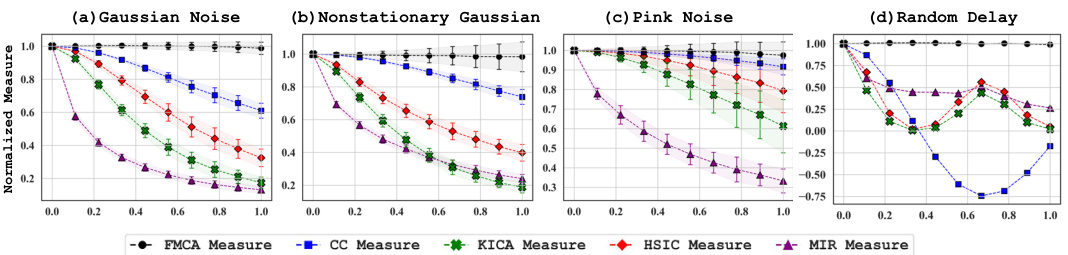
This figure demonstrates the robustness of the FMCA-T method against different types of noise and delays. Four subplots show the performance of FMCA-T and several baseline methods (CC, KICA, HSIC, MIR) under increasing levels of (a) Gaussian noise, (b) non-stationary Gaussian noise, (c) pink noise, and (d) random delays. The results show that FMCA-T maintains high accuracy and stability across all noise conditions, outperforming the baseline methods. The plot highlights the robustness of FMCA-T even when delays cause the signals to shift out of phase, leading to negative estimations with the simpler CC method.

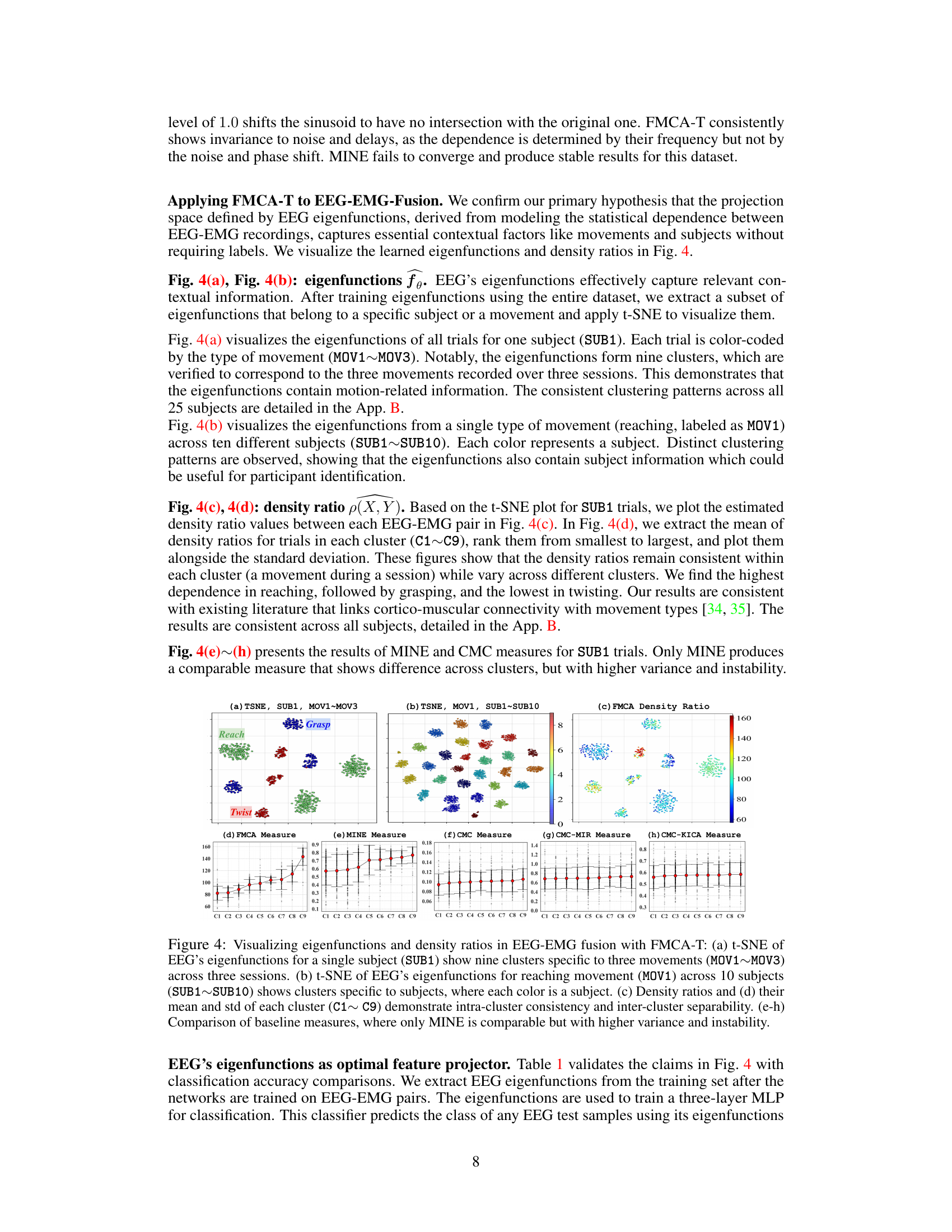
This figure visualizes the results of applying the FMCA-T method to EEG and EMG data from the EEG-EMG-Fusion dataset. Panel (a) shows t-SNE visualizations of EEG eigenfunctions for a single subject, colored by movement type, revealing distinct clusters corresponding to different movements across sessions. Panel (b) shows similar visualizations but with eigenfunctions from multiple subjects performing the same movement, demonstrating subject-specific clustering. Panel (c) displays a t-SNE plot of the density ratios, and (d) shows the mean and standard deviation of those density ratios for the clusters in (c), demonstrating consistent density ratio values within each cluster (movement) and differences across clusters. Finally, panels (e-h) compare the results of FMCA-T to several baseline methods, highlighting the superior stability and performance of FMCA-T.

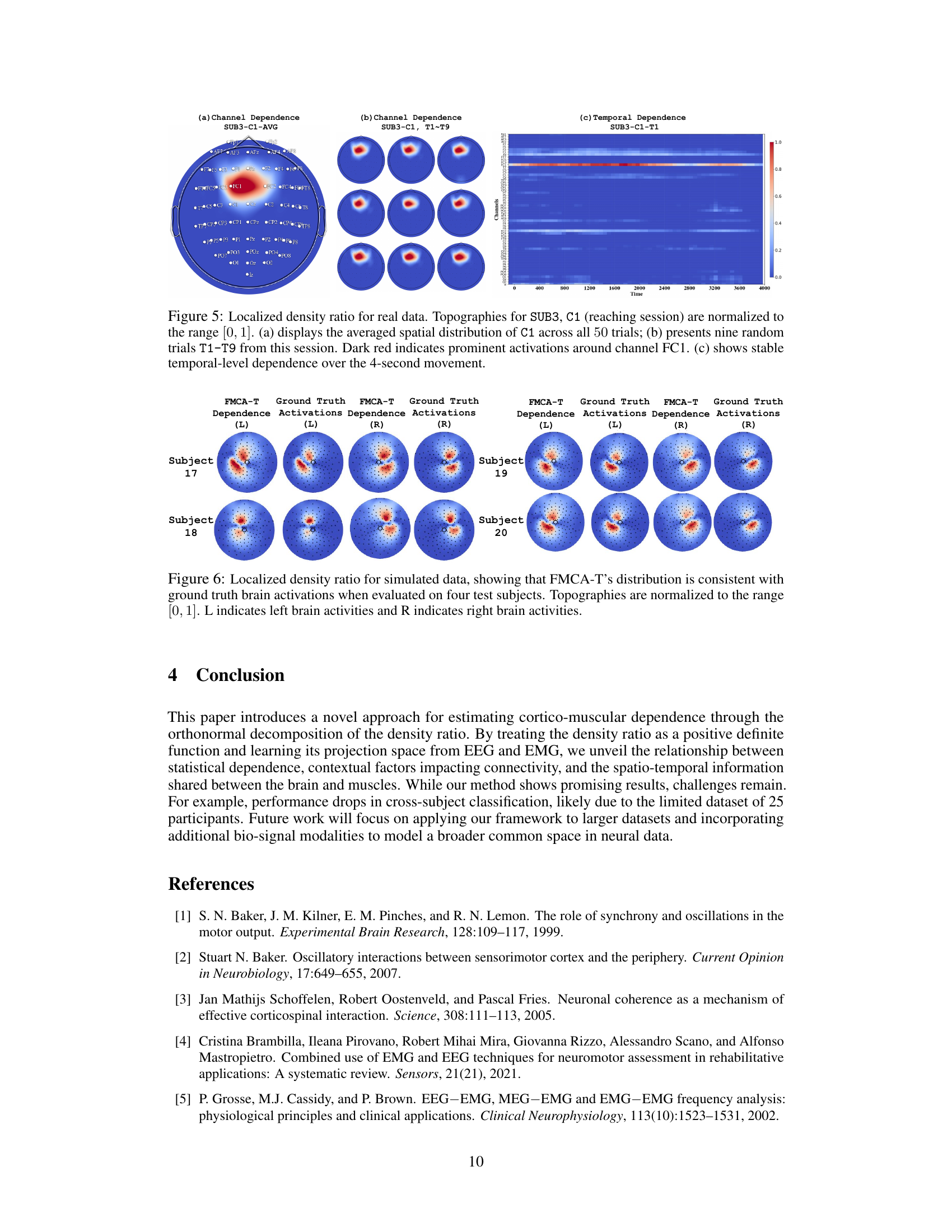
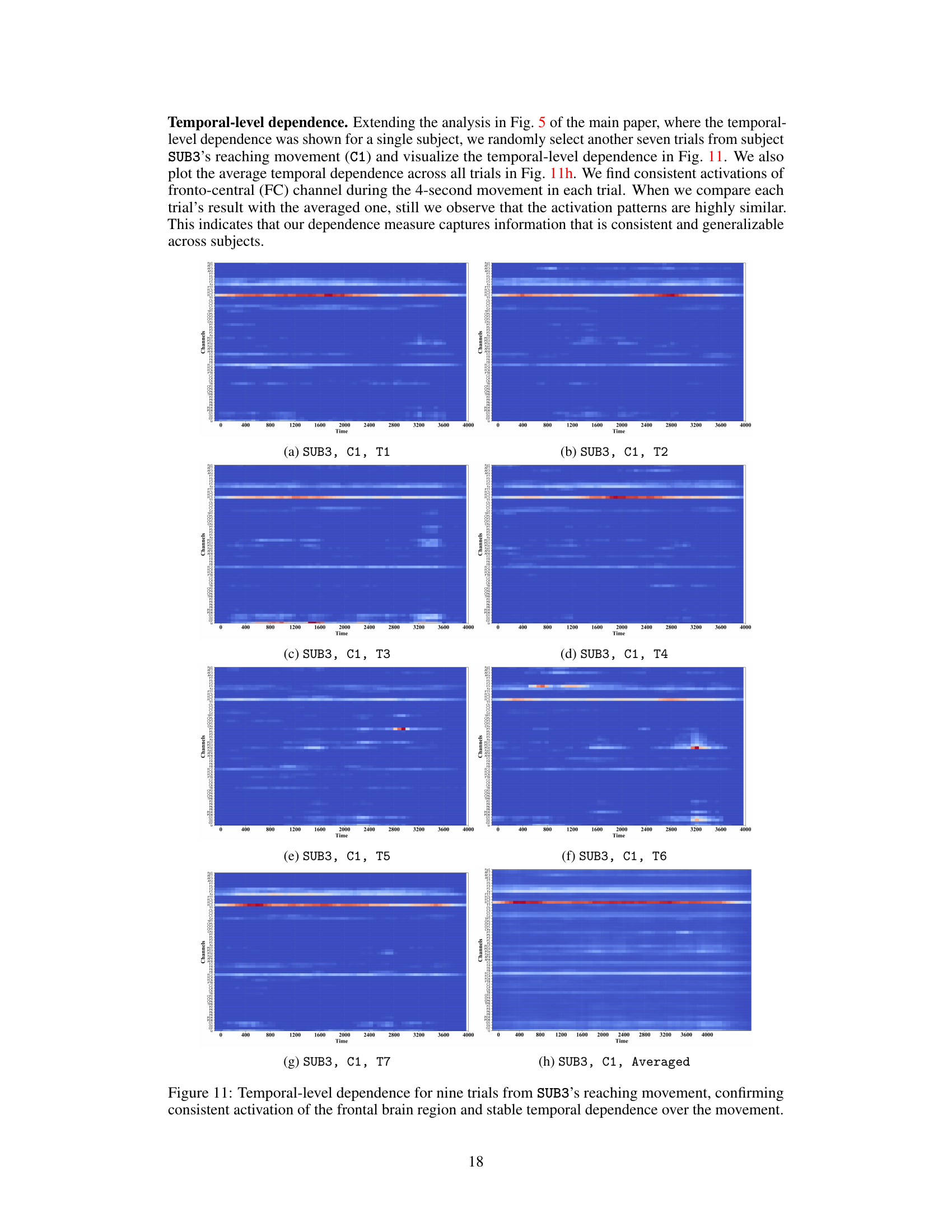
This figure visualizes the localized density ratios computed using FMCA-T for a reaching movement performed by subject SUB3. Panel (a) shows the average spatial distribution of density ratios across all 50 trials of the movement, highlighting activations in fronto-central (FC) areas of the brain. Panel (b) displays the spatial distribution of density ratios for nine randomly selected trials (T1-T9) from this same session. Panel (c) illustrates the temporal dynamics of density ratios for trial T1, demonstrating stable temporal dependence throughout the 4-second movement.
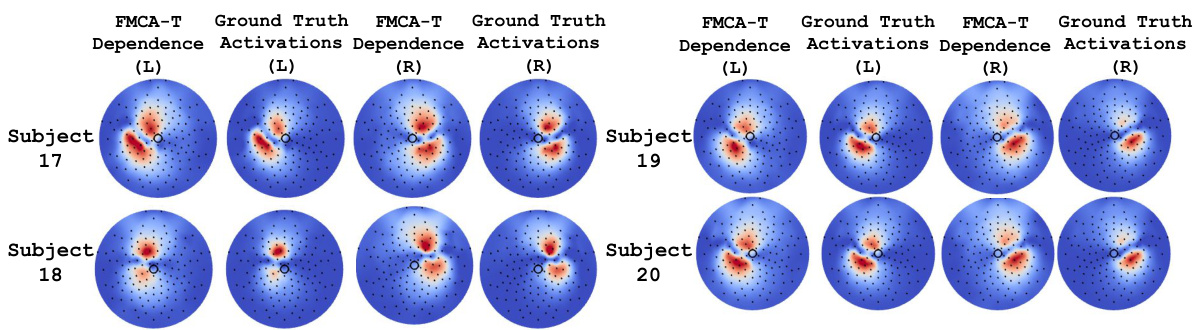
This figure visualizes the results of applying the proposed FMCA-T method to a simulated EEG-EMG dataset. It compares the spatial distribution of density ratios obtained from FMCA-T with the ground truth brain activations. The results demonstrate that the method accurately captures the location and intensity of brain activation patterns, indicating its effectiveness in identifying brain regions involved in cortico-muscular interactions.

This figure illustrates the proposed framework for learning cortico-muscular dependence through density ratio decomposition. It shows how EEG and EMG signals are processed by neural networks to estimate the density ratio, which is then decomposed into eigenvalues and eigenfunctions. The eigenfunctions are used as feature projectors to capture contextual information (movements, subjects), and a further analysis is performed to investigate channel-level and temporal-level dependencies.
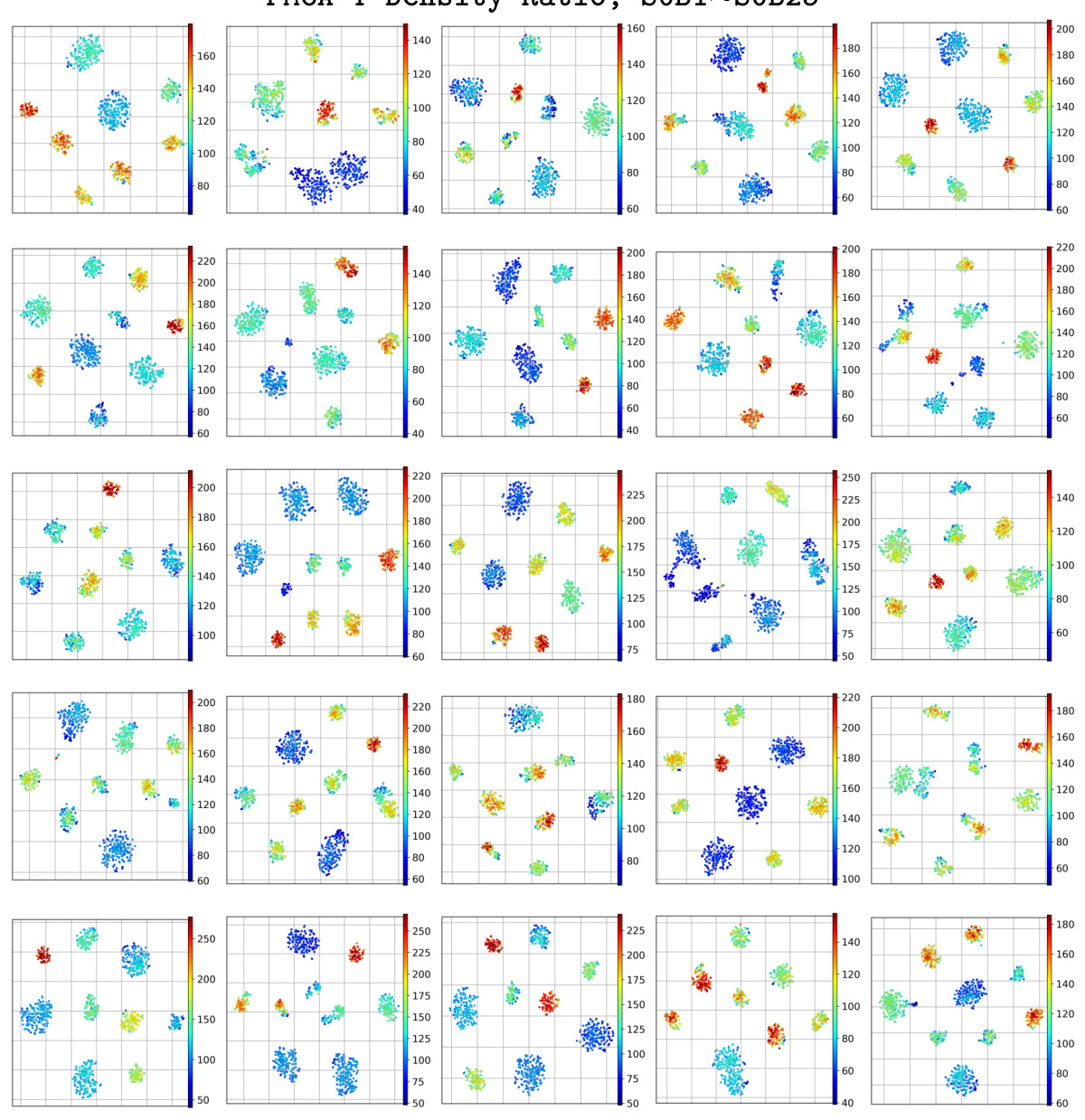
This figure visualizes the results of applying the FMCA-T method to EEG-EMG data. Panel (a) shows t-SNE plots of EEG eigenfunctions for a single subject, demonstrating clear separation of clusters corresponding to different movements performed across multiple sessions. Panel (b) shows similar t-SNE plots but for a single movement (reaching) across multiple subjects, revealing subject-specific clustering patterns. Panel (c) displays the density ratios calculated from the EEG and EMG data, illustrating the high-level dependence between the two signals. Panel (d) shows the mean and standard deviation of these density ratios for each cluster. Finally, panels (e) through (h) compare the performance of FMCA-T with other baseline methods for measuring statistical dependence between EEG and EMG data.

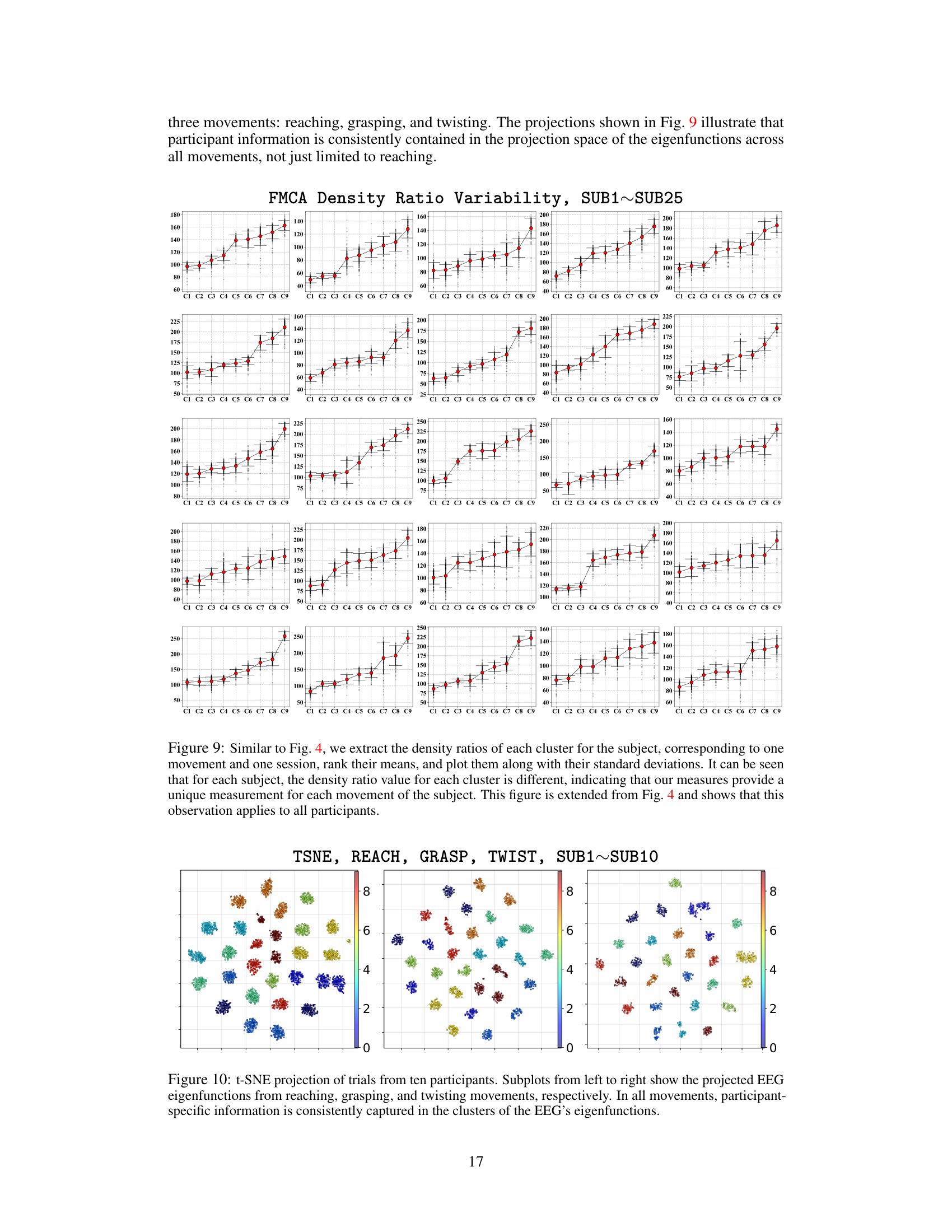
This figure visualizes the t-SNE projections of EEG eigenfunctions obtained from 25 participants’ data. Each point represents a single trial, and the color of the point indicates the density ratio, which reflects the strength of the cortico-muscular dependence. The trials are grouped into clusters based on their density ratios. Consistent patterns across all participants indicate that the eigenfunctions effectively capture the movements and that the density ratio is a reliable measure of cortico-muscular dependence.

This figure visualizes the results of applying the FMCA-T method to EEG and EMG data. Panel (a) shows t-SNE visualizations of EEG eigenfunctions for a single subject, revealing distinct clusters corresponding to different movements performed across multiple sessions. Panel (b) shows similar visualizations but across multiple subjects, demonstrating that the eigenfunctions also capture subject-specific information. Panels (c) and (d) present the density ratios and their statistics, highlighting consistent values within clusters and significant differences between them. Panels (e) through (h) compare the FMCA-T results to other methods for evaluating statistical dependence, indicating that FMCA-T demonstrates superior stability and accuracy.
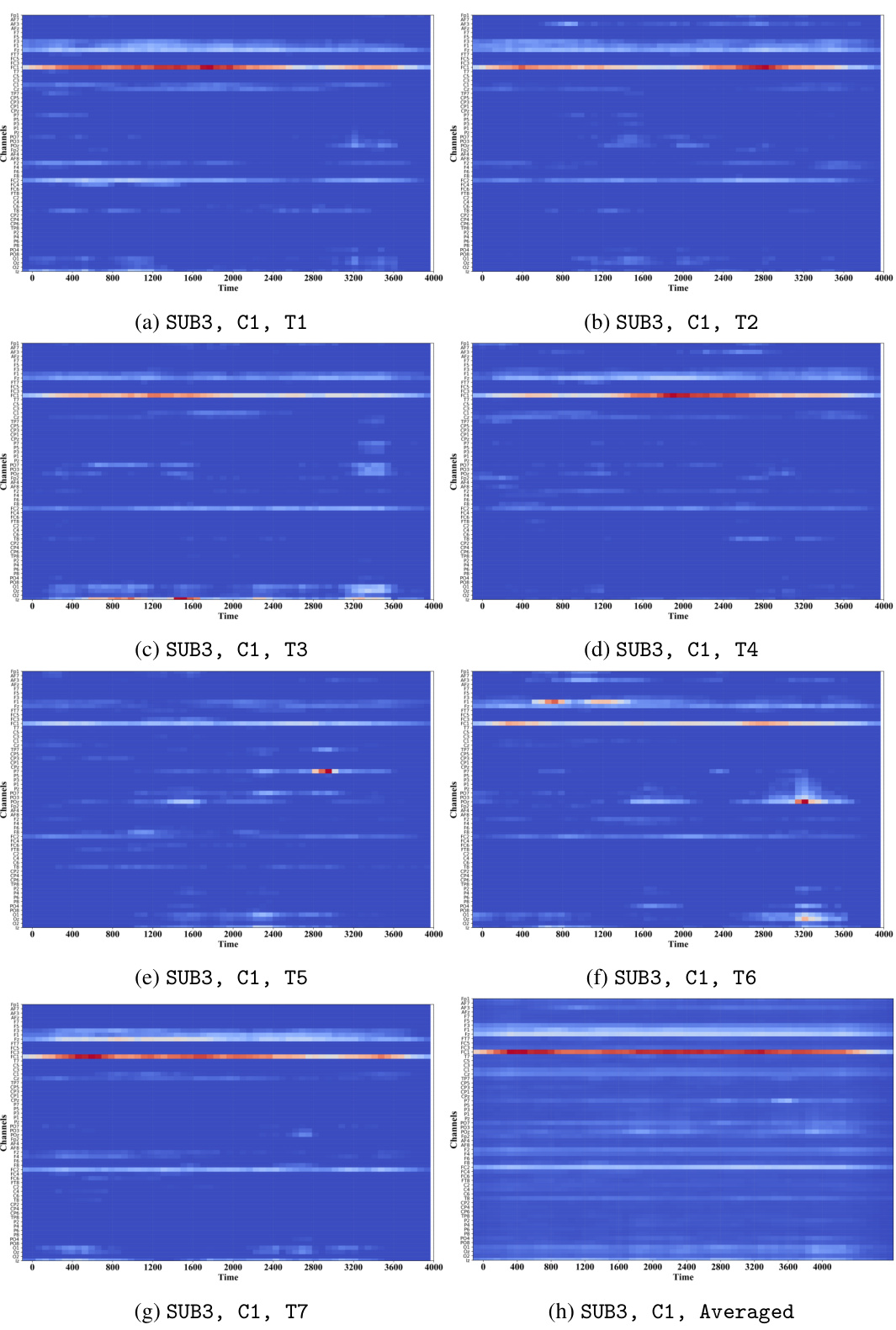
This figure visualizes the localized density ratio for real EEG and EMG data during a reaching movement. Panel (a) shows the average spatial distribution across all trials for channel C1 of subject SUB3, highlighting activation in fronto-central (FC) areas. Panel (b) displays the spatial distribution for nine randomly selected trials from the same subject and channel, demonstrating consistent activation patterns. Panel (c) illustrates the temporal dependence for one trial, showing stable activation over the 4-second movement duration.
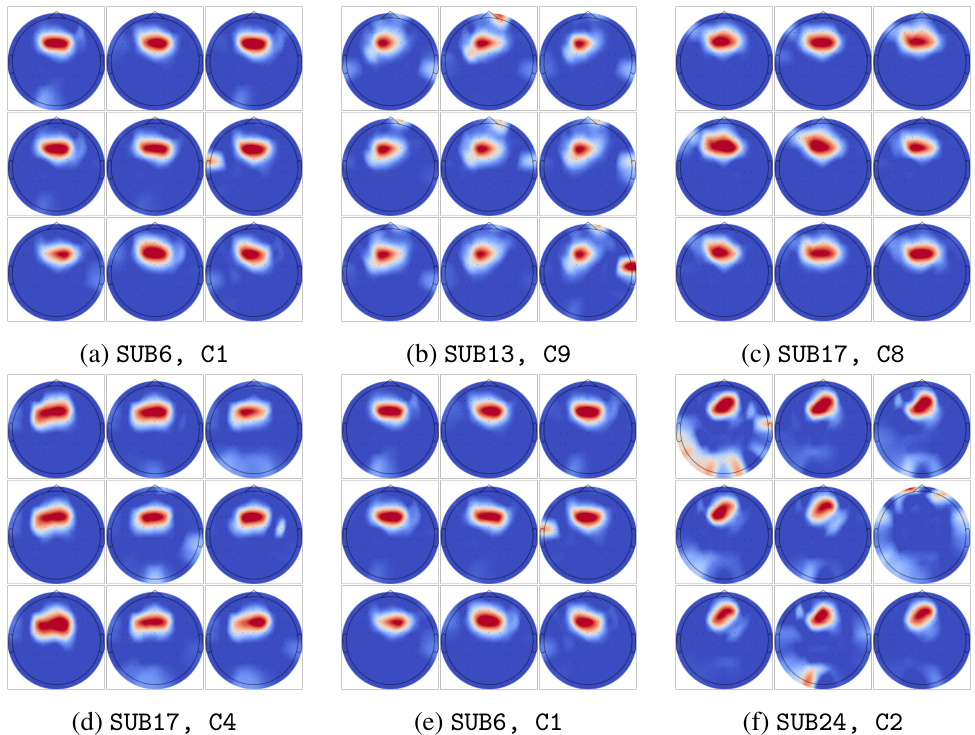
This figure visualizes channel-level dependencies by showing activation patterns across different subjects and clusters. The results consistently highlight strong activations in the fronto-central (FC) areas, suggesting their importance in classifying movements and contributing significantly to cortico-muscular connectivity.
This figure demonstrates the robustness of the FMCA-T method against various types of noise and delays. Four subplots show how the density ratio, calculated using FMCA-T, remains relatively stable even with added Gaussian noise (stationary and non-stationary), pink noise, and random delays. The stability of FMCA-T is contrasted with other methods (MIR, CC, KICA, HSIC) which show decreased performance in the presence of noise and delays. The results highlight FMCA-T’s ability to accurately capture the underlying signal patterns despite data corruption.

This figure visualizes the localized density ratios computed using the proposed method on the SinWav dataset under different delay levels. The top row shows the density ratios calculated from the clean signal, while the bottom row uses the delayed signal. The results demonstrate the method’s ability to accurately capture the period and phase of the signals, even with added delays.
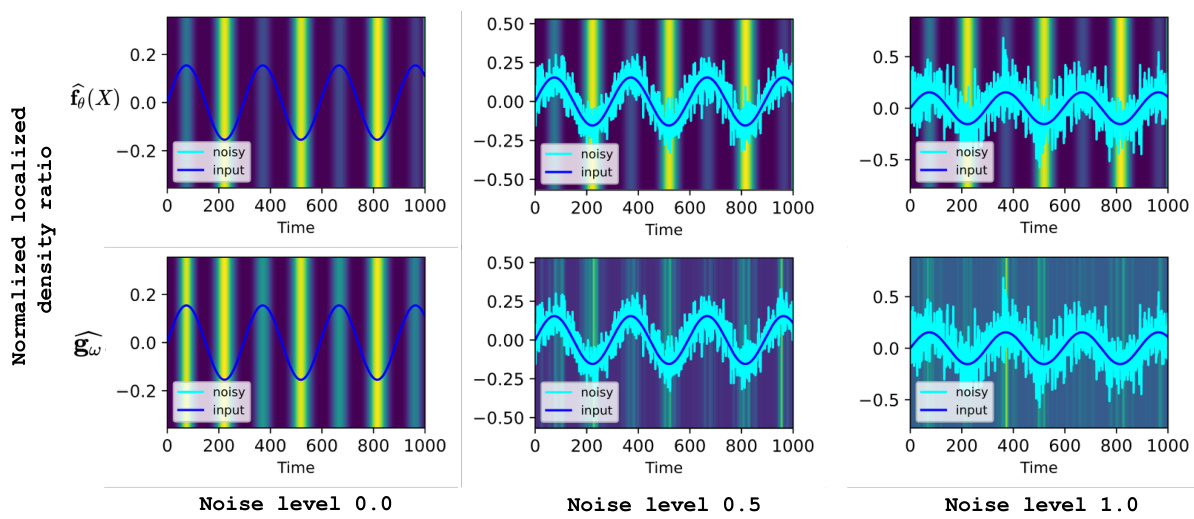
This figure demonstrates the robustness of the FMCA-T method against various types of noise and random delays. Four subfigures show the performance of FMCA-T and other methods (MIR, CC, KICA, HSIC) under different noise conditions: stationary Gaussian noise, non-stationary Gaussian noise, non-stationary pink noise and random delays. The results show that FMCA-T is the most robust method, especially when delays increase.
More on tables

This table compares the classification accuracy achieved by different methods, including supervised, self-supervised, and the proposed method (FMCA-T). The key finding is that FMCA-T significantly outperforms other methods, especially in cross-subject settings, demonstrating the effectiveness of using learned EEG eigenfunctions as feature projectors for classification. Importantly, the EMG data is only needed during training, not testing, highlighting the efficiency and potential of this approach.
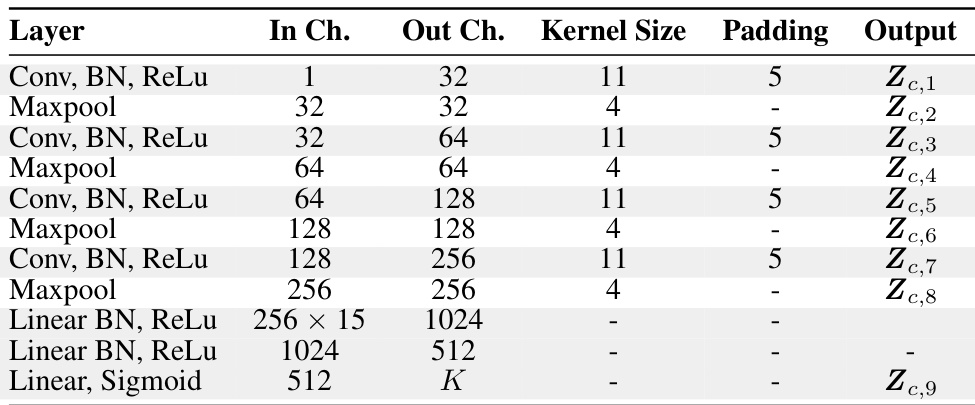
This table details the architecture of the temporal network used in the proposed method. It shows the layers of the network, including convolutional layers, max-pooling layers, and fully connected layers. For each layer, the number of input channels, output channels, kernel size, padding, and the output feature map are listed. The temporal network processes single-channel EEG signals to extract spatiotemporal features.
Full paper#