↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Training large AI models is computationally expensive, and the communication between the many computers involved is a major bottleneck. Current methods use high-precision gradients, leading to high communication costs. This is especially problematic for large models. This work addresses this by using the Lion optimizer, which leverages the sign operator to reduce precision.
The paper introduces Distributed Lion, a novel distributed training algorithm based on the Lion optimizer. It communicates only binary or low-precision vectors, drastically cutting communication costs. Experiments on vision and language tasks show that Distributed Lion achieves performance comparable to standard optimizers with far less bandwidth usage. This improvement is particularly significant for large models where communication is a significant hurdle.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly reduces the communication overhead in distributed training of large AI models. This is a critical bottleneck in current deep learning research. The proposed method, Distributed Lion, achieves comparable performance to standard optimizers while requiring significantly less communication bandwidth, making it highly relevant to researchers focusing on scalability and efficiency of AI model training. It also opens up new avenues for research into efficient distributed optimization algorithms and their theoretical analysis.
Visual Insights#

This figure illustrates the workflow of the Distributed Lion algorithm. Each worker maintains its own optimizer state and computes a binary update vector using the Lion optimizer. These vectors are then sent to a central server which aggregates them using either majority voting or averaging to produce a final update vector. This final vector is then sent back to the workers to update their model parameters. This process significantly reduces communication cost compared to traditional methods.

This table compares the bandwidth requirements of various distributed training methods, including the proposed Distributed Lion and existing methods such as Global Lion/AdamW, TernGrad, and DGC. It shows the amount of data transferred between workers and the server for both sending gradients and receiving updates. The key takeaway is that Distributed Lion significantly reduces the communication overhead compared to the baseline methods.
In-depth insights#
Lion Optimizer#
The Lion optimizer, a recent advancement in the field of AI, presents a compelling alternative to established optimizers like AdamW. Its core strength lies in its simplicity and efficiency, requiring less memory and computation while demonstrating comparable performance. This is achieved through the strategic use of the sign function, simplifying the update rule and leading to reduced computational overhead. The sign-based nature also allows for efficient communication in distributed training environments, as exemplified by the proposed Distributed Lion algorithm, which reduces communication costs significantly by exchanging only binary or low-precision vectors. The theoretical analysis supports the convergence properties of both Lion and Distributed Lion, emphasizing its robustness and potential advantages for training large AI models. However, further research is needed to completely understand the nuances of Lion’s behavior and how it interacts with different dataset characteristics and problem settings. Further exploration of Lion’s capabilities in various architectures and its adaptability to different training paradigms is needed to solidify its position among top-tier optimizers.
Distrib. Lion#
The heading ‘Distrib. Lion’ cleverly suggests a distributed version of the Lion optimizer, a novel algorithm known for its memory and computational efficiency. The core idea likely involves adapting Lion’s sign-based updates for distributed training environments, minimizing communication overhead. This could be achieved via techniques like binary or low-precision gradient aggregation. Reducing the communication bandwidth is crucial for scaling up training of large models; this is the main benefit of Distrib. Lion. The approach likely demonstrates robustness across different tasks, batch sizes, and worker counts, showcasing its practical applicability in large-scale distributed training settings. It likely compares favorably to existing methods such as deep gradient compression, highlighting its unique advantages in balancing performance and communication efficiency. Theoretical analysis of convergence properties is likely included, providing a solid foundation for the proposed method. Overall, Distrib. Lion is presented as a significant advancement in efficient distributed optimization.
Convergence#
The convergence analysis section of the paper is crucial for establishing the reliability and effectiveness of the proposed Distributed Lion optimization algorithm. It rigorously examines the algorithm’s ability to reach a solution, focusing on two key phases. Phase I demonstrates rapid convergence towards a feasible solution set, while Phase II focuses on minimizing the objective function within that set. The analysis uses a constrained optimization framework, incorporating assumptions about the data distribution, smoothness of the objective function, and the behavior of the algorithm’s momentum. The method of analysis is noteworthy as it leverages a surrogate metric to measure convergence in Phase II, a more flexible approach compared to standard methods. The paper offers separate convergence results for the averaging and majority vote aggregation mechanisms, providing a deeper understanding of the algorithm’s behavior under different aggregation strategies. The theoretical results are carefully supported by assumptions and detailed proofs, adding credence to the algorithm’s practical applicability. Ultimately, the convergence analysis is critical for establishing the theoretical foundation upon which the algorithm’s empirical success rests.
Comm. Efficiency#
The research paper’s section on communication efficiency focuses on minimizing communication overhead in distributed training. Distributed Lion, a novel algorithm, is presented as a solution. By leveraging the sign operator inherent in the Lion optimizer, Distributed Lion significantly reduces the bandwidth requirements of distributed training. The core innovation lies in communicating only binary or low-precision vectors between workers and the central server, in contrast to the typical high-precision gradients. Two variants are explored: one using averaging, the other majority voting, for aggregation of these updates. Theoretical analysis supports the convergence properties of both variants, confirming their efficacy despite this reduced precision. Experimental results show that Distributed Lion achieves comparable performance to methods using full-precision gradients but with substantially lower communication costs, highlighting its practical effectiveness in large-scale model training.
Future Work#
The ‘Future Work’ section of a research paper on Distributed Lion for efficient distributed training could explore several promising avenues. Extending the algorithm to handle non-i.i.d. data is crucial for real-world applications. The current algorithm assumes identically and independently distributed (i.i.d.) data across worker nodes, a simplification often not met in practice. Investigating its robustness and performance under various levels of data heterogeneity would significantly increase its practical value. Combining Distributed Lion with other communication-efficient techniques, such as gradient compression or sparsification, could yield even greater efficiency gains. A deeper theoretical analysis focusing on convergence rates under different data distributions and network conditions would further enhance our understanding. Finally, empirical evaluation on a wider range of large-scale models and tasks is vital for demonstrating the scalability and generalizability of the algorithm. The exploration of these directions could solidify Distributed Lion’s position as a leading method for large-scale model training.
More visual insights#
More on figures
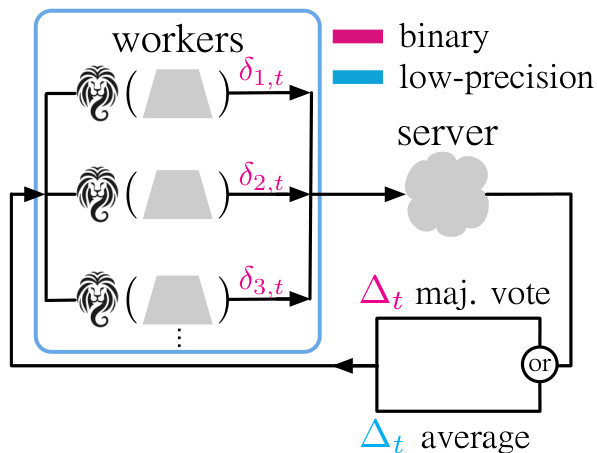
The figure illustrates the architecture of Distributed Lion. Multiple worker nodes each run a local instance of the Lion optimizer, producing a binary update vector. These vectors are sent to a central server, which aggregates them using either majority voting or averaging, resulting in a final update vector. The server then distributes this aggregated vector back to the worker nodes for model parameter updates. This process minimizes communication overhead by transmitting only low-precision vectors.
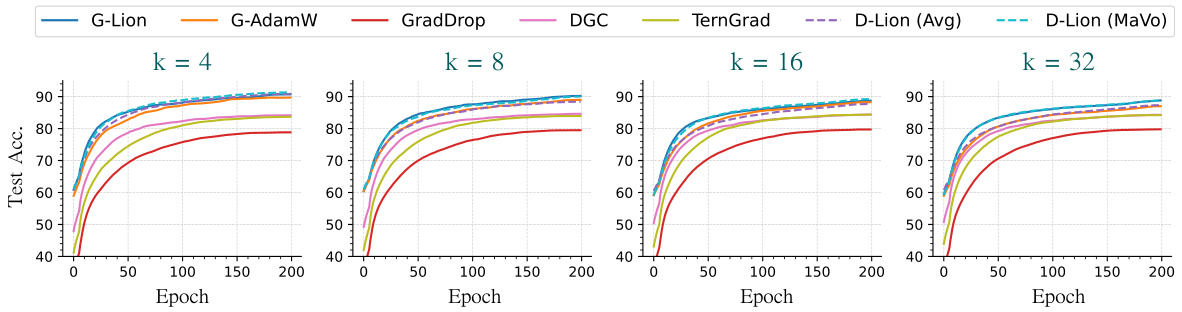
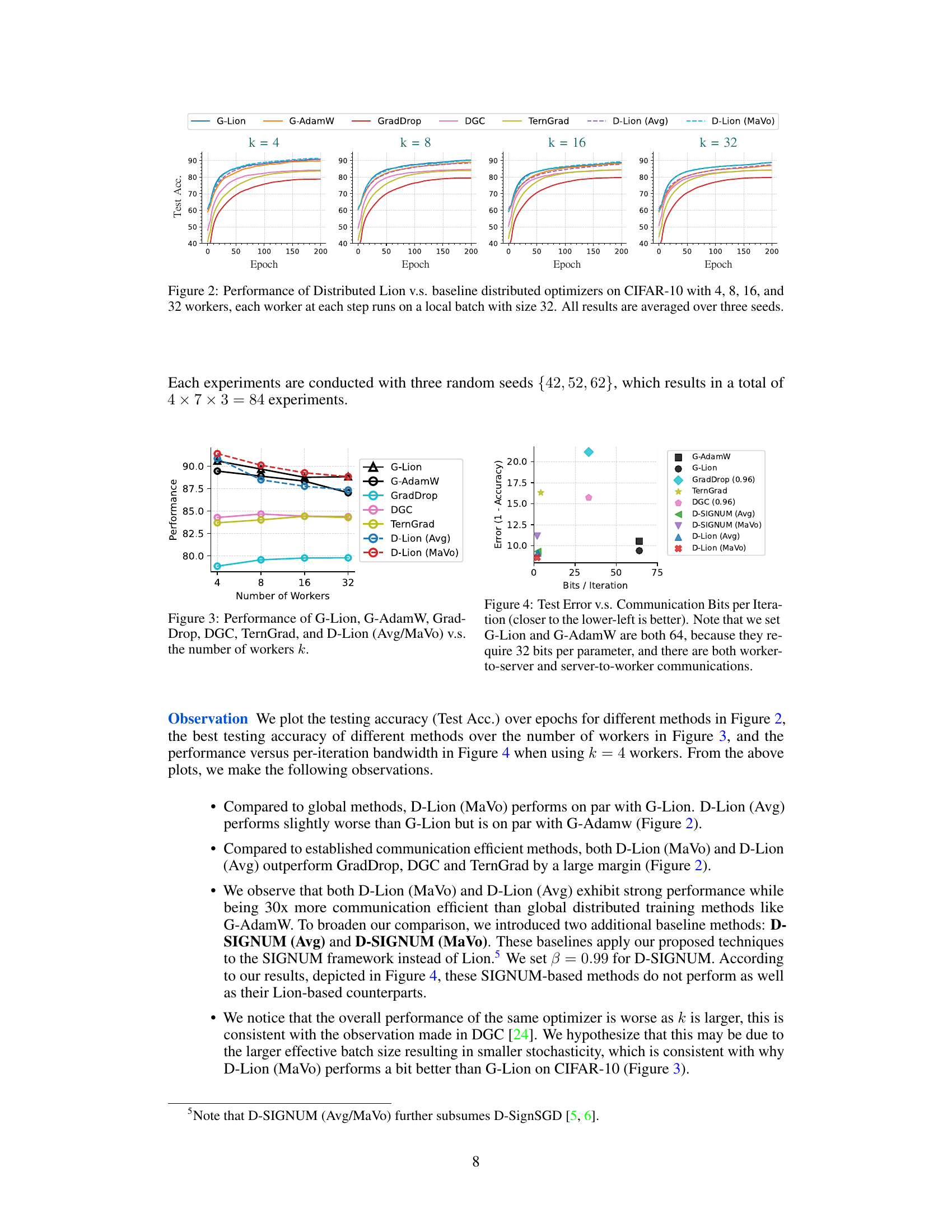
This figure compares the performance of Distributed Lion (with averaging and majority vote aggregation methods) against several baseline distributed optimizers on the CIFAR-10 dataset. The experiment varies the number of workers (4, 8, 16, and 32), and each worker processes a local batch size of 32. The results, averaged over three random seeds, illustrate the test accuracy over 200 epochs for each method. This helps to visualize the convergence speed and final accuracy of different optimization strategies in a distributed setting.

This figure compares the performance of different distributed optimizers against the number of workers used. The plot shows that the Global Lion (G-Lion) and Global AdamW (G-AdamW) optimizers consistently outperform most of the communication-efficient methods, specifically TernGrad, GradDrop, and DGC. However, the Distributed Lion methods (D-Lion (Avg) and D-Lion (MaVo)), using either averaging or majority voting aggregation, demonstrate a competitive performance, particularly D-Lion(MaVo), approaching the performance of the global methods. This highlights the effectiveness of Distributed Lion in reducing communication overhead while maintaining good performance.
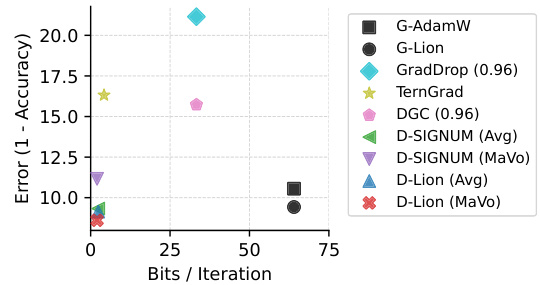
This figure compares the performance (test error) of various distributed optimization methods against their communication cost (bits per iteration). It shows that Distributed Lion (MaVo and Avg) achieve a favorable trade-off, attaining comparable performance to global methods like G-Lion and G-AdamW while using significantly less communication bandwidth. Other low-bandwidth methods such as TernGrad, GradDrop, and DGC are also included for comparison.
More on tables
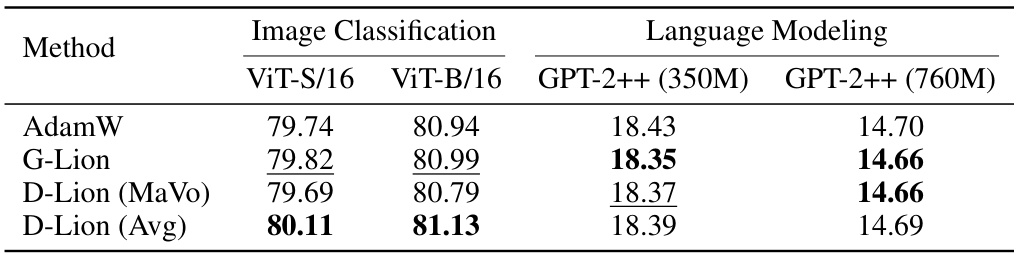
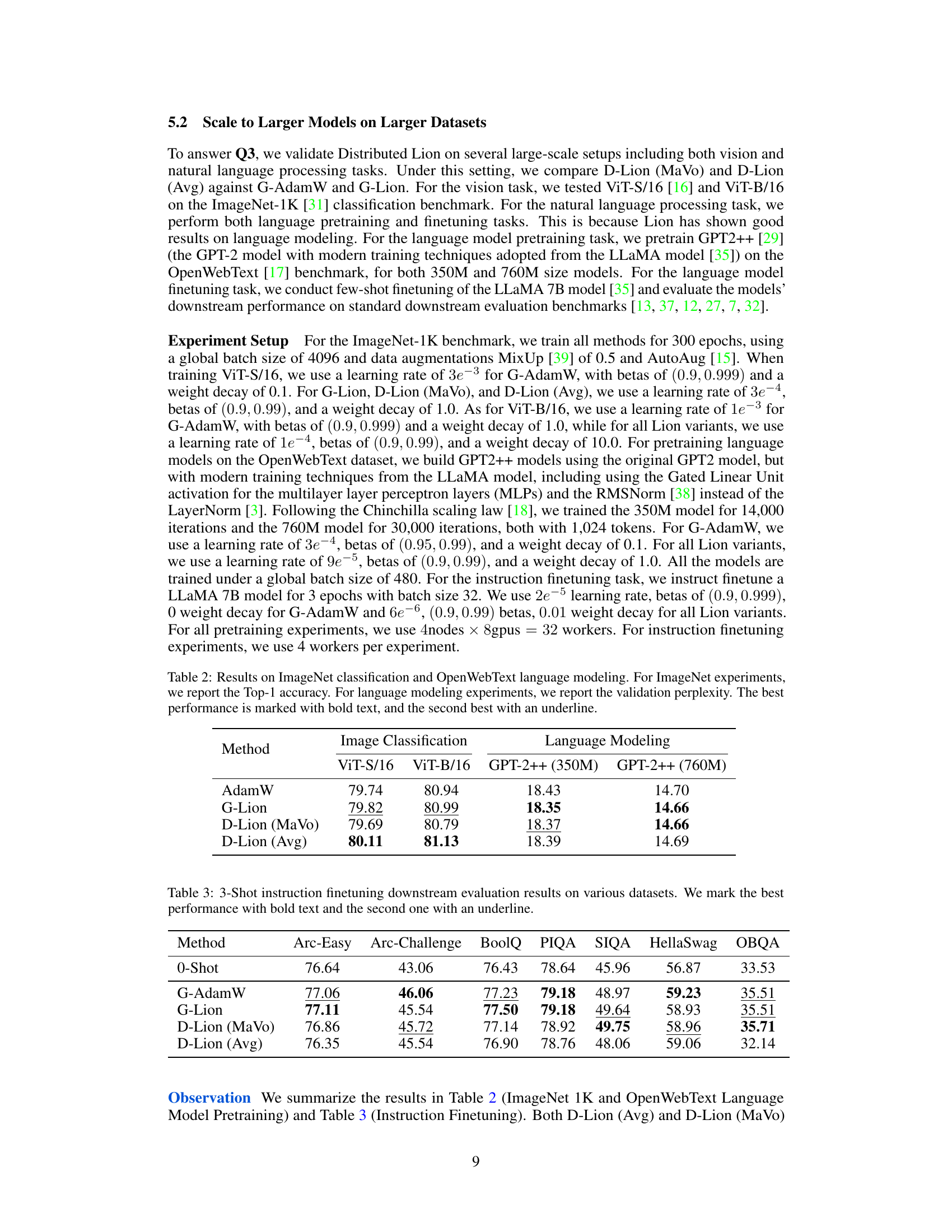
This table presents the results of experiments conducted on ImageNet (image classification) and OpenWebText (language modeling) datasets using different optimization methods: AdamW, G-Lion, D-Lion (MaVo), and D-Lion (Avg). For ImageNet, Top-1 accuracy is reported. For language modeling, validation perplexity is shown. The best performing method for each task and model size is highlighted in bold, while the second-best is underlined. This table allows comparison of the performance and efficiency of different optimizers on large-scale tasks.
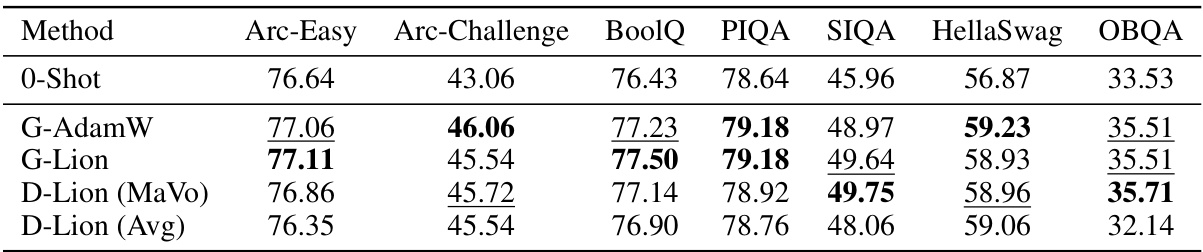
This table presents the results of a 3-shot instruction finetuning experiment on various downstream datasets. The models were finetuned using different optimization methods: G-AdamW, G-Lion, D-Lion (MaVo), and D-Lion (Avg). The table displays the performance of each method on several datasets, including Arc-Easy, Arc-Challenge, BoolQ, PIQA, SIQA, HellaSwag, and OBQA. The best performing method for each dataset is highlighted in bold, and the second best is underlined. This allows for a direct comparison of the performance and relative effectiveness of the different optimization methods in a few-shot learning context.
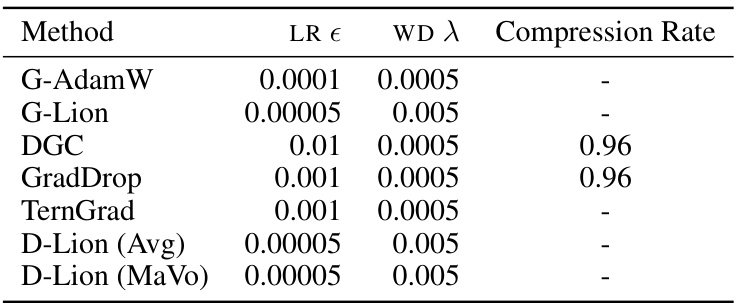
This table lists the hyperparameters used for each optimization method in the experiments shown in Figure 2 of the paper. It includes the learning rate (LR), weight decay (WD), and compression rate for each method. The compression rate is relevant for methods that employ gradient compression techniques (DGC, GradDrop). The table clarifies the settings used to produce the results presented visually in the accompanying figure.
Full paper#