One-Layer Transformer Provably Learns One-Nearest Neighbor In Context

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it theoretically proves a single-layer transformer can learn a complex non-parametric model (1-NN). This bridges the gap between the empirical success of transformers and our theoretical understanding of their capabilities, opening avenues for analyzing their in-context learning abilities. It also highlights the significance of the softmax attention mechanism.

Visual Insights

#

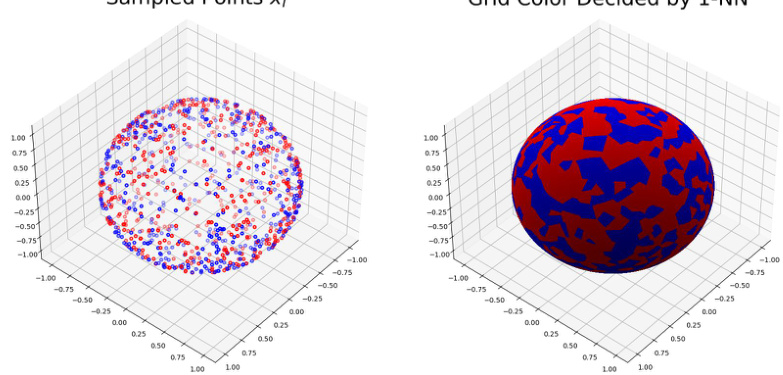
This figure illustrates the data distribution used in the paper’s theoretical analysis. The left panel shows sampled points on a 2D sphere, colored red or blue based on their label (y = 1 or y = -1). The right panel shows the same sphere, but now colored according to the one-nearest-neighbor (1-NN) prediction rule. Each point’s color represents the label of its nearest neighbor among the sampled points, demonstrating how the 1-NN rule partitions the sphere.

In-depth insights

#

1-NN via Transformers

#

The concept of ‘1-NN via Transformers’ explores the intriguing intersection of classical machine learning algorithms and the modern deep learning architecture of transformers. It investigates whether a simple one-layer transformer, leveraging its attention mechanism, can effectively mimic the functionality of a one-nearest neighbor (1-NN) classifier. This is significant because it bridges the gap between the theoretical understanding of simpler models and the complex behavior of deep learning. Successfully demonstrating this capability would imply that the attention mechanism implicitly captures essential aspects of proximity-based reasoning. Moreover, it would provide a concrete example of how transformers can learn nonparametric methods, moving beyond the previously studied linear regression cases and offering valuable insights into the underlying mechanisms of in-context learning. The approach would involve training a transformer on labeled data using a suitable loss function. The success would be measured by the extent to which the transformer’s predictions match those of a 1-NN algorithm, highlighting the potential for transformers to implement more complex nonparametric methods. Such an achievement would shed light on the learning capabilities of transformers, potentially leading to more efficient and explainable models.

Softmax Attention

#

Softmax attention, a core mechanism in transformer networks, plays a crucial role in enabling these models to process sequential data effectively. It operates by calculating a weighted average of input vectors, where the weights are determined by the softmax function applied to attention scores. These scores represent the relevance of each input vector to the current processing step. The softmax function ensures that the weights are non-negative and sum to one, allowing for a probabilistic interpretation of the attention mechanism. A key strength of softmax attention is its ability to capture long-range dependencies, as the attention scores allow the model to focus on relevant information regardless of its position in the sequence. However, the computational cost of softmax attention can be significant, scaling quadratically with the sequence length. This limitation has prompted the development of alternative attention mechanisms that aim to improve efficiency without sacrificing performance. Furthermore, the non-convexity of the loss function associated with training softmax attention models poses challenges for optimization. This leads to difficulty in analyzing and establishing theoretical guarantees for the optimization process. Despite these challenges, softmax attention remains a highly successful and widely used mechanism, underpinning many state-of-the-art results in various natural language processing applications. Future research will likely focus on improving its efficiency and developing a more thorough theoretical understanding of its behavior and limitations.

Convergence Proof

#

A rigorous convergence proof for a machine learning model is crucial for establishing its reliability and predictability. Such a proof typically involves demonstrating that the model’s parameters converge to a stable solution under a specific optimization algorithm, such as gradient descent. Key aspects of a convergence proof include defining precise assumptions about the data distribution, loss function, and model architecture. The proof strategy often relies on mathematical tools from optimization theory and numerical analysis to bound the error and demonstrate its convergence to zero. Challenges in proving convergence can stem from the non-convexity of the loss function, requiring specialized techniques like analyzing the optimization landscape or showing convergence to a local minimum under specific conditions. Establishing convergence guarantees is paramount for ensuring that the algorithm learns the target function reliably and efficiently, ultimately leading to a robust model that generalizes well to unseen data. A successful convergence proof strengthens the theoretical foundation of the machine learning model.

Distribution Shift

#

The concept of ‘distribution shift’ is crucial in evaluating the robustness and generalizability of machine learning models. In the context of the provided research paper, distribution shift refers to how well the model trained on one data distribution performs on data drawn from a different distribution. This is especially important for in-context learning where the model relies heavily on the examples given in a prompt. The paper investigates how a one-layer transformer, trained to perform one-nearest neighbor classification under a specific data distribution, behaves when presented with data drawn from a shifted distribution. Understanding this behavior is crucial to assessing the real-world applicability of the model. The focus on a simple, non-parametric model (1-NN) makes the theoretical analysis tractable and helps shed light on the role of attention mechanisms in achieving robustness against distribution shift. The findings contribute to our understanding of the limits and capabilities of transformers in a wider context beyond idealized conditions.

Future ICL Research

#

Future research in In-Context Learning (ICL) should prioritize bridging the gap between empirical observations and theoretical understanding. While impressive ICL capabilities have been demonstrated, the underlying mechanisms remain unclear. A key area is developing more robust theoretical frameworks that can explain ICL’s success across diverse tasks and model architectures. This includes investigating the role of different architectural components, such as attention mechanisms, and exploring the impact of various training strategies. Focus on generalization is crucial; current ICL models often struggle with distribution shifts and unseen data, demanding research into improving robustness and out-of-distribution generalization. Exploring the connection between ICL and other machine learning paradigms—like meta-learning and few-shot learning—offers exciting avenues for developing more efficient and effective ICL methods. Finally, practical applications and societal implications of ICL should be carefully considered, driving research toward responsible and beneficial deployment of these powerful techniques.

More visual insights

#

More on figures

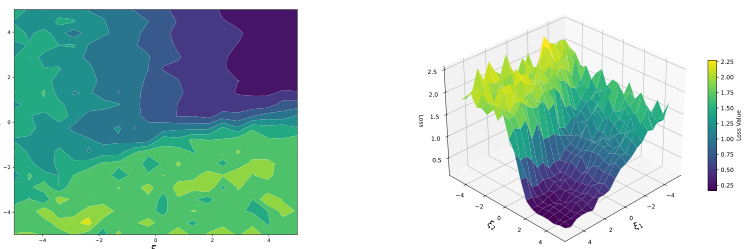
The figure visualizes the loss landscape of a single-layer transformer trained to perform one-nearest neighbor classification. It displays both a heatmap and a 3D surface plot showing how the loss function varies with two parameters, §1 and §2, which represent weights in the transformer’s attention layer. The training data is generated according to Assumption 1 with d=N=4, implying data points on a 3D sphere (d-1 dimensions) and a sample size of 4. The highly non-convex and irregular nature of the loss landscape is clearly demonstrated, making the optimization problem challenging.

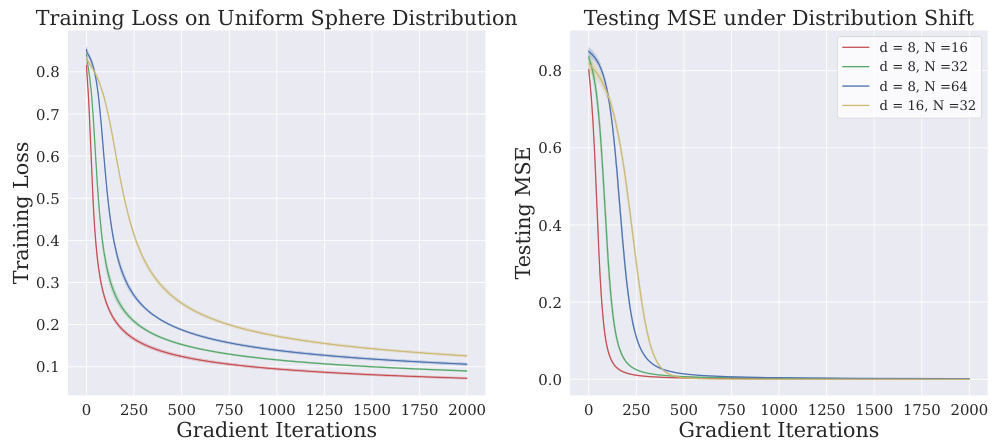
This figure shows the training and testing results of a single-layer transformer trained on a one-nearest neighbor task. The left panel displays the training loss convergence for different dataset sizes and input dimensions, demonstrating successful minimization of the loss function despite its non-convex nature. The right panel illustrates the model’s performance on a testing dataset with a different distribution than the training data. Despite the distribution shift, the model exhibits low mean squared error (MSE), closely matching the performance of a one-nearest neighbor classifier.

Full paper

#