↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Offline reinforcement learning (RL) methods like Decision Transformer struggle in adversarial settings where an opponent actively works against the agent. This is because the training data may not represent the worst-case scenarios the agent might encounter at test time. Standard methods, conditioned on the highest return, may choose actions that perform poorly against a strategic adversary.
The paper proposes Adversarially Robust Decision Transformer (ARDT). ARDT enhances robustness by training the model to anticipate and counteract the worst-case outcomes. The model is conditioned on the minimax return, learning strategies that perform well even when facing powerful, adaptive adversaries. ARDT shows significant improvements on benchmark tasks, demonstrating superior robustness and higher worst-case returns compared to existing methods.
Key Takeaways#
Why does it matter?#
This paper is important because it significantly advances the robustness of offline reinforcement learning in adversarial environments. It introduces a novel algorithm, Adversarially Robust Decision Transformer (ARDT), which outperforms existing methods in various settings. This work addresses a critical challenge in applying RL to real-world scenarios where agents must contend with unpredictable and potentially malicious adversaries, opening new avenues for research in safety-critical applications. The insights provided are crucial for improving the reliability and security of autonomous systems.
Visual Insights#
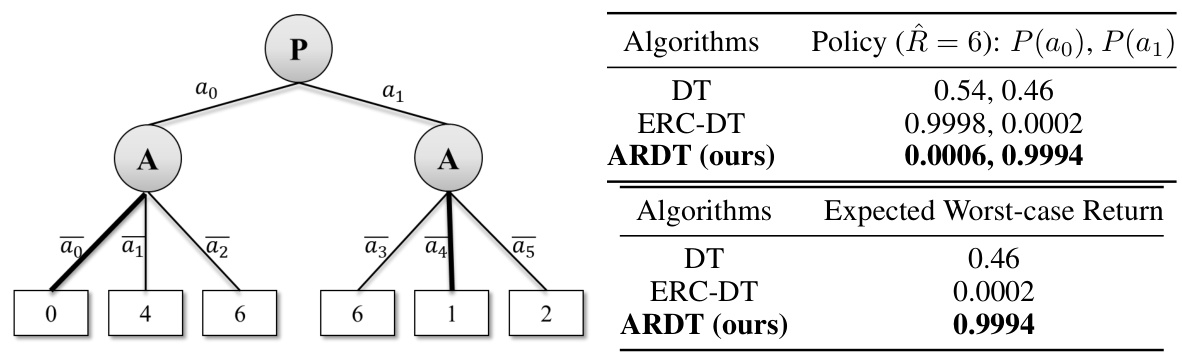
This figure demonstrates a simple sequential game to illustrate the robustness of the proposed Adversarially Robust Decision Transformer (ARDT) against an adversary. The left-hand side (LHS) shows the game tree, where the decision-maker (P) chooses an action, followed by the adversary (A), resulting in a final reward. The right-hand side (RHS) presents the action probabilities and worst-case returns obtained by three different algorithms (DT, ERC-DT, and ARDT) when trained on uniformly collected data with full trajectory coverage. The results highlight ARDT’s superior ability to select the robust action (a1) that maximizes the worst-case return, unlike DT and ERC-DT.

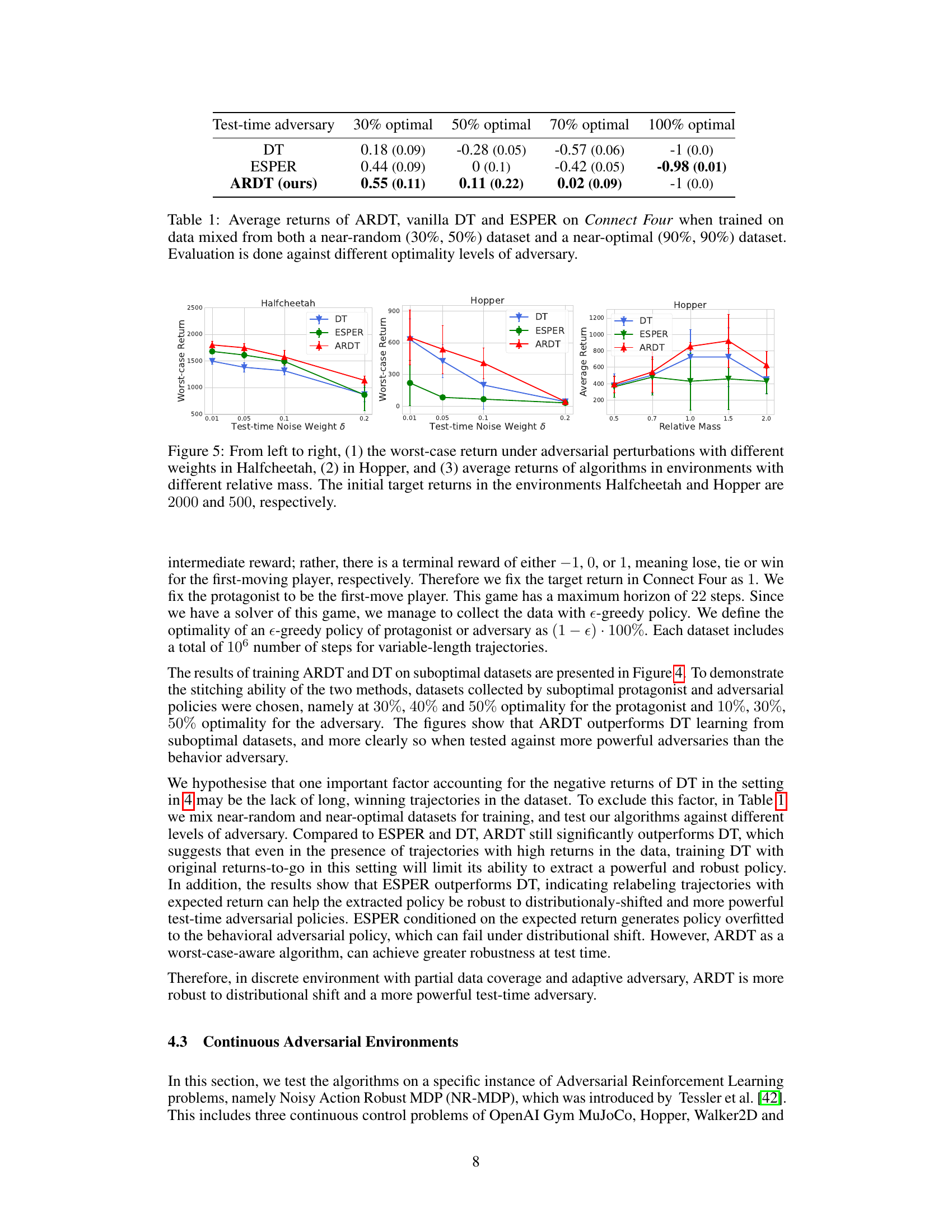
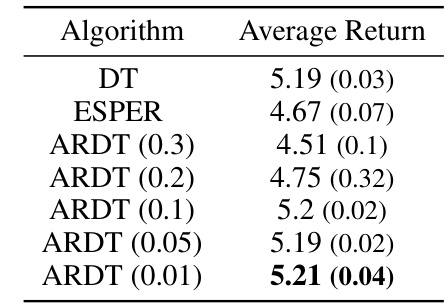
This table presents the average returns achieved by three different algorithms (ARDT, DT, and ESPER) when trained on datasets containing a mix of near-random and near-optimal trajectories. The performance is evaluated against adversaries with varying levels of optimality (30%, 50%, 70%, and 100%). The results show how the different algorithms perform under different adversary strengths and highlight the improved robustness of ARDT.
In-depth insights#
Adversarial RvS#
Adversarial RvS (Reinforcement Learning via Supervised Learning) tackles the challenge of training robust RL agents in adversarial environments. Standard RvS methods often fail in such scenarios because they overfit to the training data, which may not reflect the behavior of a powerful adversary at test time. Adversarial RvS addresses this by explicitly considering the worst-case scenarios during training, learning policies that are robust against various adversarial strategies. This often involves techniques like minimax optimization or adversarial training to enhance the agent’s resilience and maximize its worst-case performance. A key benefit of Adversarial RvS is its ability to improve the generalization of RL agents to unseen or adversarial environments, leading to more reliable and trustworthy decision-making in real-world applications.
Minimax Returns#
The concept of “Minimax Returns” in adversarial reinforcement learning focuses on finding the optimal strategy for a decision-maker in a worst-case scenario. It involves calculating the minimum expected return that can be achieved, considering the adversary’s optimal counter-strategy. This approach is crucial for creating robust policies that perform well even when facing powerful adversaries. Minimax Returns directly address distributional shift problems encountered during offline learning. By optimizing for the worst-case scenario, the policy becomes more robust to unexpected changes in the adversary’s behavior during deployment. The core idea is to relabel trajectories using the estimated in-sample minimax returns-to-go, enabling the decision transformer to learn policies conditioned on these more robust estimates, instead of possibly overly optimistic returns. This technique results in significantly improved worst-case performance over existing methods, demonstrating greater resilience to adversarial actions, which is particularly beneficial in challenging and uncertain environments.
ARDT Algorithm#
The Adversarially Robust Decision Transformer (ARDT) algorithm presents a novel approach to enhance the robustness of Decision Transformers (DTs) in adversarial environments. ARDT’s core innovation lies in its use of minimax expectile regression to relabel trajectories with worst-case returns-to-go. This crucial step effectively conditions the policy on the most challenging scenarios, thereby improving its resilience against powerful, test-time adversaries. Unlike standard DTs that learn from potentially misleading trajectories—where high returns might be achieved due to suboptimal adversary behavior—ARDT directly targets a maximin equilibrium strategy. This approach is particularly effective in offline RL settings where the distribution of adversary policies during training may differ significantly from test-time. By aligning the target return with the worst-case return, ARDT effectively mitigates distributional shifts, thereby achieving superior performance in games with full data coverage and continuous adversarial RL environments with partial data coverage. The algorithm’s use of expectile regression is particularly advantageous for its avoidance of out-of-sample estimation and its capacity to approximate minimax values efficiently, improving both the accuracy and training efficiency of the model. Overall, ARDT offers a significant improvement in robustness compared to conventional DT methods, demonstrating its value for a wide array of applications where adversarial robustness is paramount.
Robustness Tests#
A robust model should perform well under various conditions and not be overly sensitive to small changes. In a research paper, a section on ‘Robustness Tests’ would be crucial for evaluating the model’s ability to withstand various challenges. The tests should cover several aspects: First, it should assess the model’s performance when presented with noisy or incomplete data, simulating real-world scenarios where perfect information is unavailable. Next, the test should investigate the impact of distributional shifts, where the characteristics of the data encountered during deployment differ from those seen during training. Adversarial attacks, designed to intentionally mislead the model, are also important to simulate malicious inputs. The results of these tests should be carefully analyzed, potentially using statistical measures, to quantitatively assess the model’s robustness. Ultimately, a comprehensive ‘Robustness Tests’ section allows for a well-rounded evaluation of the model’s reliability and practical applicability, ensuring that its performance is not merely an artifact of favorable training conditions.
Future Work#
Future research directions stemming from this work could explore extending ARDT to handle stochastic environments, a significant limitation of the current approach. Investigating the impact of different minimax estimators beyond expectile regression is also warranted. Addressing partial observability in adversarial settings would significantly broaden the applicability of ARDT. Finally, exploring the effectiveness of ARDT in multi-agent scenarios beyond zero-sum games and its scalability to high-dimensional continuous control problems would be valuable future endeavors. These extensions would enhance the robustness and applicability of the proposed method in more complex and realistic scenarios.
More visual insights#
More on figures
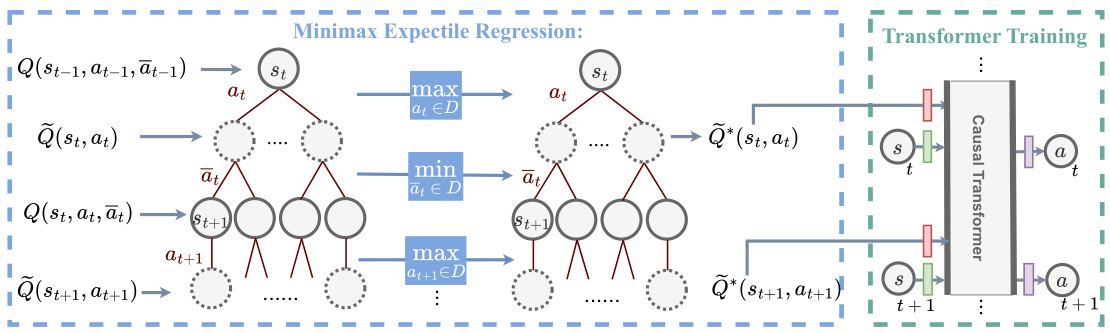
This figure illustrates the two-step training process of the Adversarially Robust Decision Transformer (ARDT). The left side shows the minimax expectile regression used to estimate the worst-case returns-to-go. This involves iteratively updating two networks: one to estimate the minimum return given the adversary’s actions, and the other to estimate the maximum return given the protagonist’s actions. The result is Q*, which represents the minimax returns-to-go. The right side shows the standard Decision Transformer (DT) training but now using Q* as the target return instead of the actual observed returns. This conditioning on worst-case returns makes the policy robust against adversarial actions.

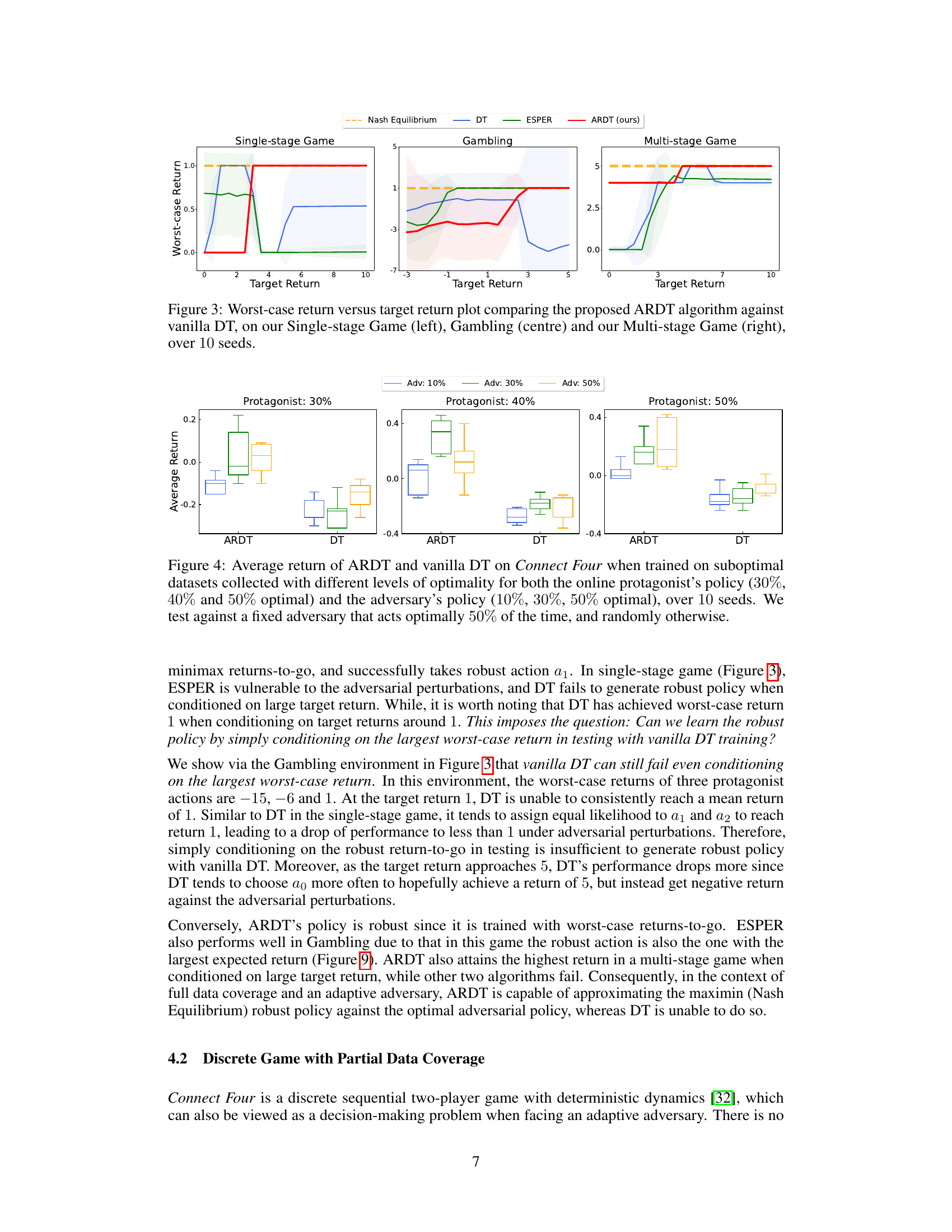
This figure compares the worst-case return achieved by three different algorithms (ARDT, DT, and ESPER) across three different game scenarios (Single-stage Game, Gambling, and Multi-stage Game) under varying target returns. The shaded regions represent the standard deviation across 10 different runs. The plot illustrates how the worst-case performance of each algorithm changes as the target return is adjusted. The results demonstrate ARDT’s superior robustness to test-time adversaries compared to DT and ESPER, particularly when the target return is high. In the single-stage game, ARDT consistently achieves the Nash Equilibrium, while DT and ESPER exhibit suboptimal worst-case performance. The Gambling and Multi-stage game results also show ARDT’s consistently better performance.

This figure displays box plots comparing the average returns achieved by Adversarially Robust Decision Transformer (ARDT) and vanilla Decision Transformer (DT) in the Connect Four game under various conditions. The training data used for both ARDT and DT was suboptimal in the sense that the data was generated by agents that were only partially optimal (30%, 40%, 50%). The testing was done against an adversary that acted optimally only 50% of the time, with the remaining actions chosen randomly. The figure shows three sets of box plots, each corresponding to a different level of optimality for the protagonist (30%, 40%, 50%), and within each set there are three box plots, one for each level of adversary optimality (10%, 30%, 50%). The results show that ARDT consistently outperforms DT.

This figure displays the performance comparison of DT, ESPER, and ARDT algorithms in three continuous control tasks under adversarial noise. The left and middle plots show the worst-case returns for Halfcheetah and Hopper respectively, as the weight of adversarial noise (δ) increases. The right plot presents the average return for Hopper as the relative mass changes. The results demonstrate ARDT’s superior robustness and higher worst-case returns compared to DT and ESPER in these adversarial environments.
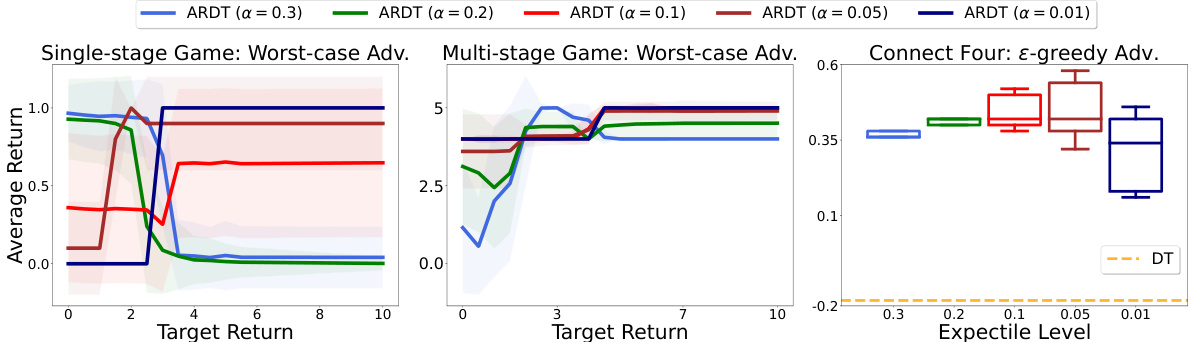
This figure displays the results of an ablation study on the impact of the expectile level (α) in the Adversarially Robust Decision Transformer (ARDT) algorithm. Three different game environments were tested: a single-stage game, a multi-stage game, and Connect Four. Each game was tested against a worst-case adversary. The results are presented as line graphs showing average return against target return for different values of α and boxplots showing the average return against the expectile level in the Connect Four game. The study reveals that a smaller α leads to better robustness in most scenarios, but in Connect Four, a too small alpha results in the algorithm acting too conservatively. Overall, the figure illustrates the importance of tuning the expectile level (α) to balance robustness and performance.

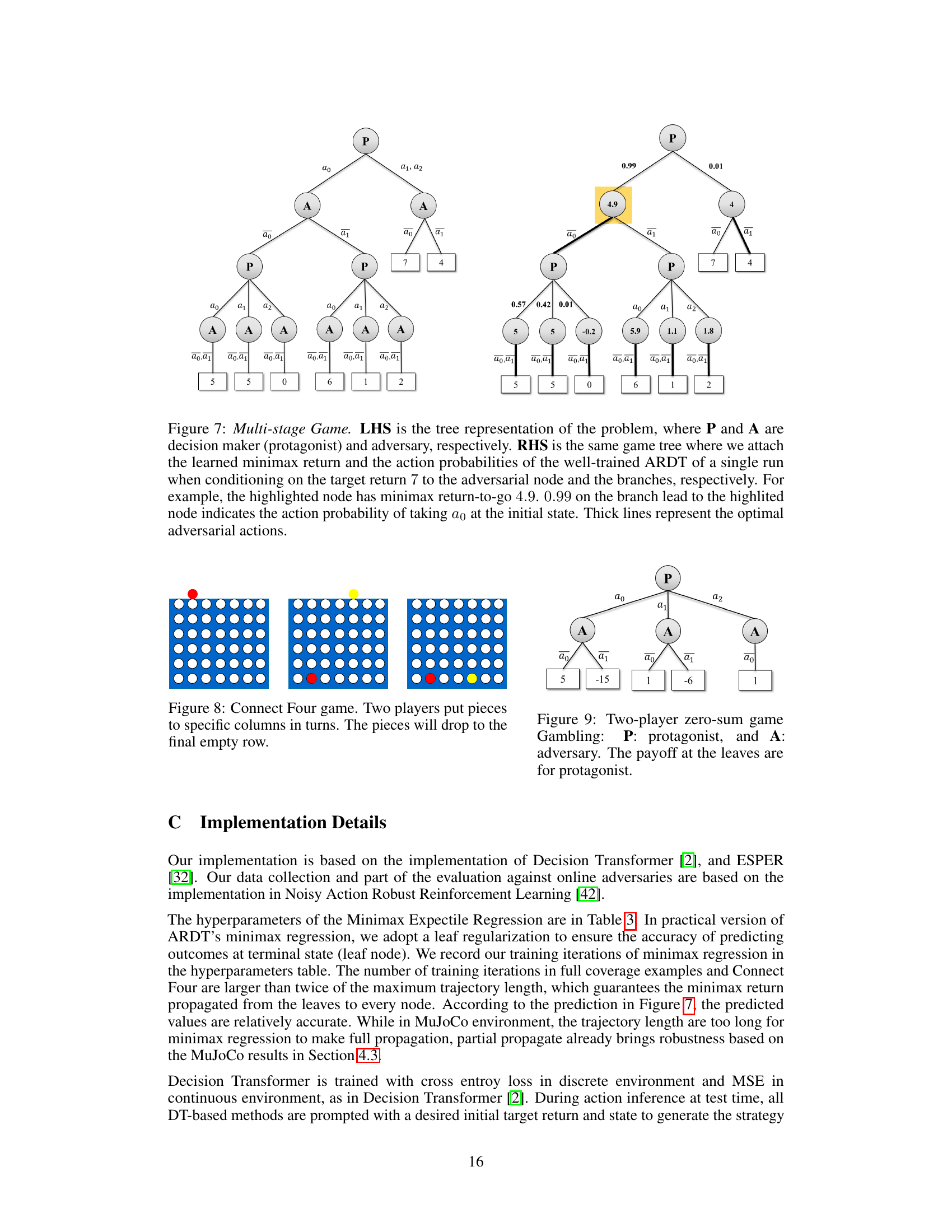
This figure illustrates a multi-stage game between a protagonist (P) and an adversary (A). The left-hand side (LHS) shows the game tree, representing the sequential decision-making process. The right-hand side (RHS) presents the same game tree, but with added information from the Adversarially Robust Decision Transformer (ARDT) model. The minimax return (the worst-case outcome for the protagonist) and action probabilities are shown for each node, highlighting the optimal strategy learned by ARDT when aiming for a target return of 7. The thicker lines indicate the optimal actions for the adversary.

This figure illustrates a game of Connect Four. It shows three different stages of the game, each with a different arrangement of red and yellow pieces. Connect Four is a two-player game where players take turns dropping colored pieces into a grid. The goal is to be the first to get four of one’s own pieces in a row—horizontally, vertically, or diagonally.

This figure shows a multi-stage game tree illustrating the decision-making process of a protagonist (P) against an adversary (A). The left side displays the game tree structure, while the right side presents the same tree augmented with minimax returns-to-go calculated by Adversarially Robust Decision Transformer (ARDT) and the corresponding action probabilities. The numbers on the leaf nodes represent the game outcomes. Highlighted nodes and thick lines emphasize the optimal adversarial actions and their probabilities based on the ARDT model.

This figure compares the worst-case return achieved by three different algorithms (ARDT, DT, and ESPER) across three different sequential games with varying target returns. The worst-case return represents the minimum return achieved when the adversary acts optimally. The x-axis shows the target return, and the y-axis displays the worst-case return obtained by each algorithm. The plot demonstrates ARDT’s superior robustness against optimal adversaries compared to DT and ESPER, particularly when the target return is high, indicating its ability to choose actions that yield high returns even in worst-case adversarial scenarios.

This figure shows a multi-stage game tree. The left-hand side (LHS) presents the game tree structure, illustrating the decision-making process of both the protagonist (P) and the adversary (A). The right-hand side (RHS) displays the same game tree augmented with information from the adversarially robust decision transformer (ARDT) model. Specifically, it shows the minimax return-to-go values at each decision node and the action probabilities calculated by ARDT when given a target return of 7. The thicker branches indicate the optimal adversarial actions according to the ARDT model.

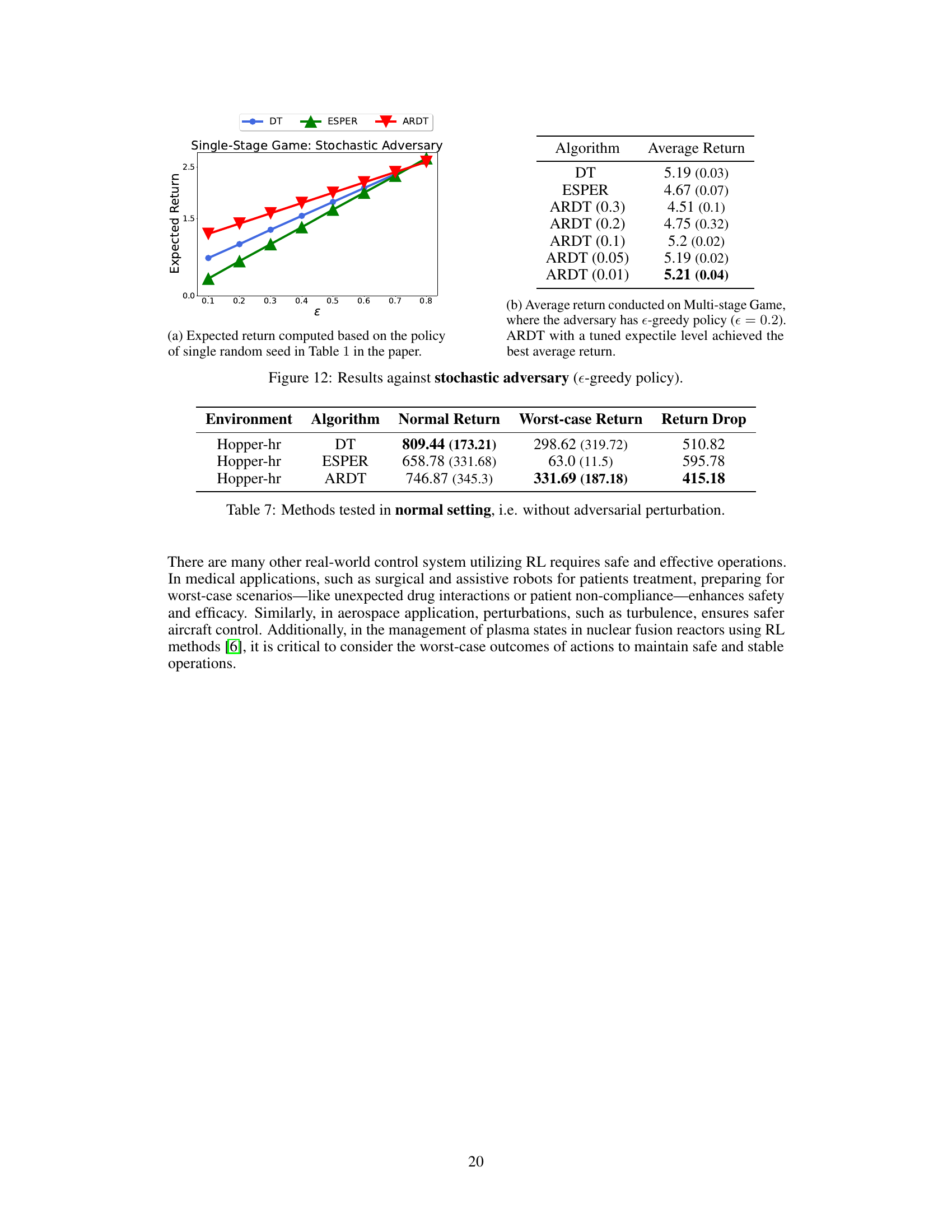
This figure compares the performance of Decision Transformer (DT), Expected Return-Conditioned Decision Transformer (ESPER), and Adversarially Robust Decision Transformer (ARDT) in a stochastic environment against an ε-greedy adversary. Subfigure (a) shows the expected return for different values of ε in a single-stage game, while subfigure (b) displays the average return in a multi-stage game with ε = 0.2. ARDT demonstrates superior performance, particularly when a well-tuned expectile level is used.
This figure presents a comparison of the worst-case return achieved by three different algorithms (ARDT, DT, and ESPER) across three different games (Single-stage Game, Gambling Game, Multi-stage Game). The x-axis represents the target return used as a condition during training, and the y-axis represents the worst-case return the algorithm achieved in a test setting with an optimal adversary. The plot shows that ARDT consistently outperforms both DT and ESPER across all three games, demonstrating its superior robustness in adversarial environments.
More on tables
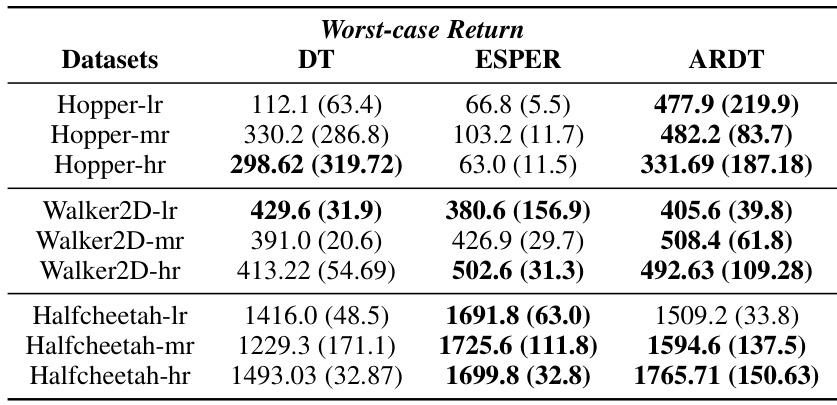
This table presents the worst-case returns achieved by Decision Transformer (DT), Expected Return-Conditioned Decision Transformer (ESPER), and Adversarially Robust Decision Transformer (ARDT) across various continuous control tasks from the MuJoCo environment. The results are obtained against eight different online adversarial policies and across five different random seeds. The data used in training included both pre-collected online datasets with high robust returns and additional random trajectories (with low, medium, and high randomness) to increase data coverage. The table shows that ARDT generally achieves higher worst-case returns compared to DT and ESPER.
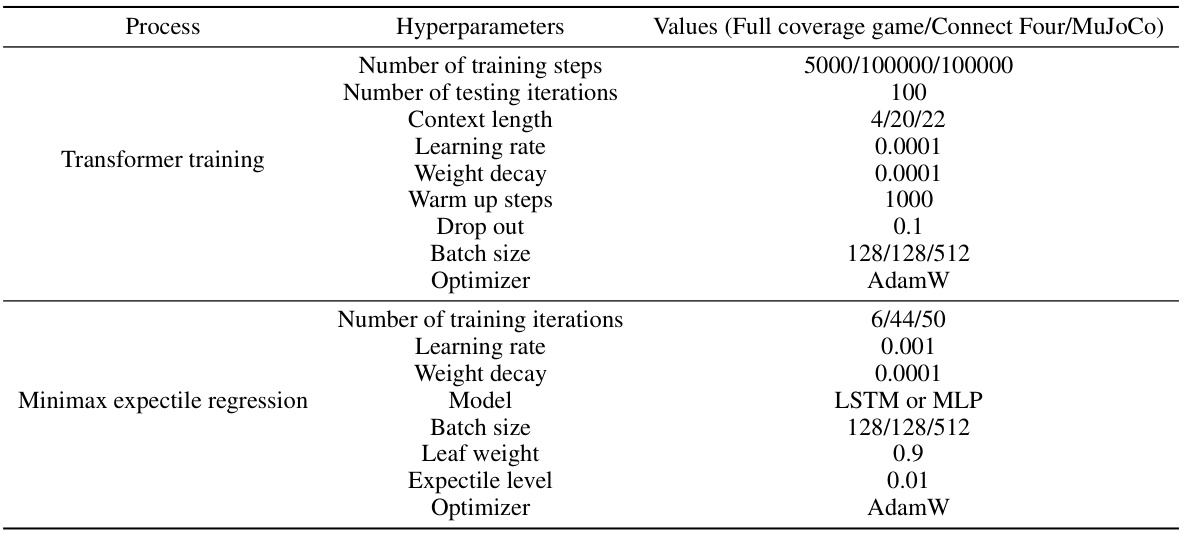
This table lists the hyperparameters used in the Adversarially Robust Decision Transformer (ARDT) algorithm. It is broken down into the hyperparameters for the transformer training phase and the minimax expectile regression phase. For each phase, it specifies the number of training steps, number of testing iterations, context length, learning rate, weight decay, warmup steps, dropout rate, batch size, optimizer, and other relevant parameters for the processes.

This table presents the returns achieved by the behavior policy (protagonist and adversary) during data collection in the MuJoCo Noisy Action Robust MDP (NR-MDP) tasks. Different levels of randomness are introduced in the data collection process, creating low (-lr), medium (-mr), and high (-hr) randomness datasets. The table shows that the behavior policy achieves varying returns depending on the task and the level of randomness.

This table presents the return of behavior policy for different optimality levels of both the protagonist and adversary in three MuJoCo environments: Hopper, Walker2D, and Halfcheetah. The optimality is defined as (1 - ε) * 100%, where ε is the exploration rate of the ε-greedy policy used to collect the data. Each tuple represents the percentage of optimality for the protagonist and the adversary, respectively. The return is the average cumulative reward obtained from the behavior policy, along with its standard deviation in parentheses. The results are shown for low, medium, and high randomness settings, indicated by the suffix -lr, -mr, and -hr, respectively.
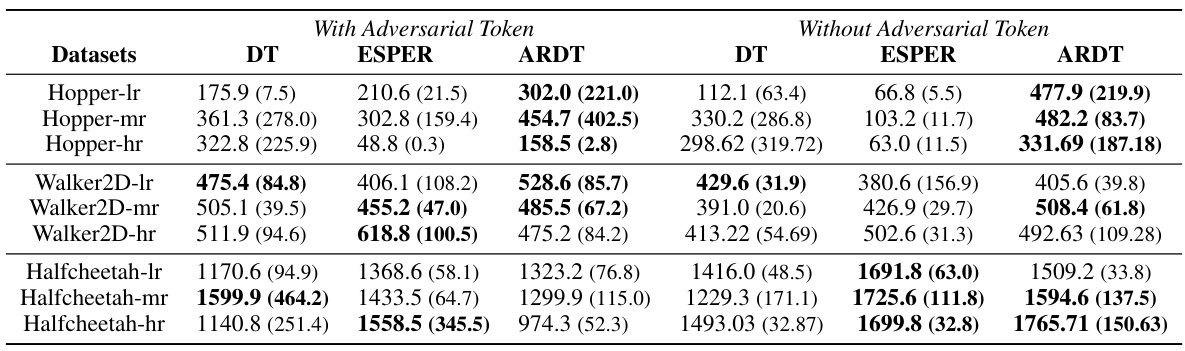
This table presents the worst-case returns achieved by Decision Transformer (DT), Expected Return-Conditioned DT (ESPER), and Adversarially Robust Decision Transformer (ARDT) across various continuous control tasks from the MuJoCo Noisy Action Robust MDP benchmark. The results are averaged across 5 random seeds and show the performance against 8 different online adversarial policies. The table further breaks down the results by including or excluding the past adversarial tokens in the model’s input, and by varying the level of randomness in the training data.

This table presents the average returns achieved by three different algorithms (ARDT, DT, and ESPER) when trained on a mixed dataset containing both near-random and near-optimal trajectories. The performance is evaluated against adversaries with varying optimality levels, showcasing the robustness of each algorithm in the face of different adversary strategies. The results highlight how ARDT outperforms DT and ESPER, especially against stronger adversaries.

This table shows the performance comparison of three algorithms (DT, ESPER, and ARDT) in a normal setting without adversarial perturbations. It presents the average normal return, the average worst-case return, and the difference (return drop) between the two for the Hopper-hr environment. The results highlight that even in the absence of adversarial attacks, ARDT shows relatively high worst-case return compared to others. Note that the numbers in parentheses are standard deviations.
Full paper#