↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multiple Choice Learning (MCL) addresses ambiguous prediction tasks by training multiple hypotheses, but it suffers from the Winner-takes-all (WTA) scheme, which promotes diversity but can lead to suboptimal solutions. The greedy nature of WTA limits exploration of the hypothesis space and can result in hypothesis collapse and convergence to poor local minima. These limitations affect the ability of MCL to accurately capture the ambiguity of the tasks.
The paper introduces Annealed Multiple Choice Learning (aMCL), which integrates simulated annealing with MCL. Annealing enhances exploration by accepting temporary performance degradations for better exploration. aMCL uses a temperature schedule to control the exploration-exploitation tradeoff. Through theoretical analysis based on statistical physics and information theory, the authors provide insights into the algorithm’s training dynamics. Extensive experiments show that aMCL outperforms standard MCL and other baselines on various datasets, demonstrating improved robustness and accuracy.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on ambiguous prediction tasks and multiple choice learning. It offers a novel solution to existing limitations, enhancing model robustness and performance. The theoretical analysis provides valuable insights into the training dynamics, while the experimental results demonstrate its effectiveness across various datasets. This opens new avenues for research in refining training strategies and exploring the interplay between exploration and optimization in machine learning.
Visual Insights#

This figure compares the performance of three different methods for handling ambiguous prediction tasks: MCL, Relaxed WTA, and Annealed MCL. Each method is visualized by its predictions (shaded circles) on a mixture of three Gaussian distributions (green points). The intensity of the circles represents the predicted scores. The figure highlights that MCL suffers from hypothesis collapse (some hypotheses are unused), while Relaxed WTA shows a bias toward the distribution’s barycenter. In contrast, Annealed MCL effectively captures the ambiguity and provides a more robust and accurate prediction.
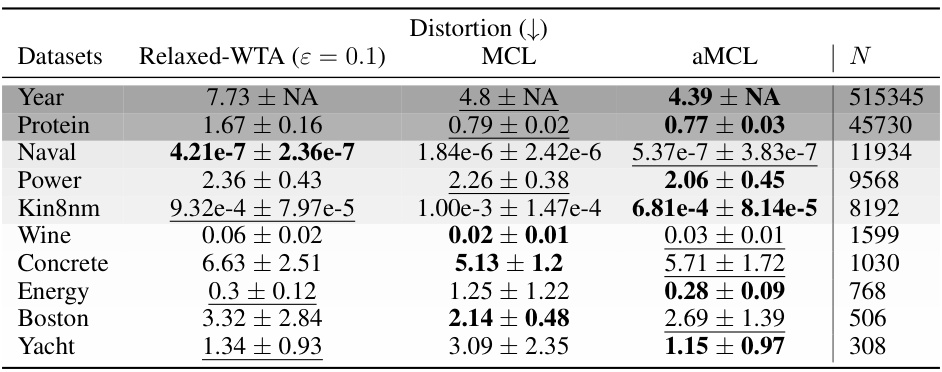
This table presents the results of the UCI regression benchmark experiments, comparing the distortion metric achieved by three different methods: Relaxed-WTA, MCL, and aMCL. The table highlights the performance of each method on various datasets, indicating the best and second-best performing methods for each dataset. The results are organized by the size of the dataset, and the best and second-best results are emphasized for clarity.
In-depth insights#
Annealed MCL Intro#
Annealed Multiple Choice Learning (aMCL) offers a novel approach to address limitations in standard Multiple Choice Learning (MCL). MCL, while effective for ambiguous prediction tasks, suffers from greedy winner-takes-all (WTA) updates that can lead to suboptimal solutions and hypothesis collapse. aMCL ingeniously integrates simulated annealing, a probabilistic technique that strategically balances exploration and exploitation of the hypothesis space. By introducing a temperature parameter, aMCL allows for a controlled exploration of the solution space, thereby mitigating the risk of getting stuck in local minima. This annealing process enhances the robustness of MCL, ultimately improving prediction accuracy and the diversity of learned hypotheses. Theoretical analysis, drawing parallels with statistical physics, further illuminates aMCL’s dynamic training trajectory and its relationship to the rate-distortion curve. The results from empirical evaluations on benchmark datasets corroborate the effectiveness of aMCL, showing considerable improvements over conventional MCL and competitive performance compared to other state-of-the-art techniques. Therefore, aMCL presents a significant advancement in handling ambiguous prediction tasks, offering a more efficient and robust method than existing MCL approaches.
aMCL Algorithm#
The core of the paper is the proposed Annealed Multiple Choice Learning (aMCL) algorithm, which enhances the standard Multiple Choice Learning (MCL) framework. aMCL addresses MCL’s limitations, primarily its tendency towards suboptimal local minima due to the greedy nature of the Winner-Takes-All (WTA) scheme. The key innovation is the integration of deterministic annealing, inspired by the gradual cooling of metals, into the MCL training process. This annealing process allows for a controlled balance between exploitation (focusing on the best hypotheses) and exploration (sampling a broader range of hypotheses), thus preventing premature convergence to poor solutions. By gradually decreasing the temperature, aMCL strategically guides the hypothesis search trajectory towards a globally optimal configuration, significantly improving robustness and overcoming the collapse issue commonly observed in MCL. The theoretical analysis leverages concepts from statistical physics and information theory to explain the algorithm’s dynamic behavior. This provides a strong theoretical foundation for the algorithm’s effectiveness and helps explain its convergence properties. Experimental validation on various datasets further demonstrates aMCL’s improved performance in comparison to MCL and other related techniques.
Theoretical Analysis#
The theoretical analysis section of this research paper delves into a comprehensive mathematical framework to support the proposed Annealed Multiple Choice Learning (aMCL) algorithm. It formally establishes the algorithm’s training dynamics as an entropy-constrained alternate minimization, connecting it to well-established concepts from statistical physics and information theory. Key contributions include characterizing the training trajectory using rate-distortion theory and providing rigorous proofs for the algorithm’s properties. The analysis clarifies the impact of the temperature schedule, revealing the critical role of phase transitions in shaping the hypothesis space exploration and ultimately converging to a robust solution. Furthermore, the analysis provides insights into how annealing mitigates the limitations of standard Winner-Takes-All methods, particularly regarding hypothesis collapse and convergence to suboptimal local minima, which are significant issues addressed by this work. The theoretical foundation ensures a deeper understanding of aMCL’s strengths and behavior, laying the groundwork for future improvements and extensions of the algorithm.
UCI Experiments#
The UCI experiments section likely evaluates the proposed Annealed Multiple Choice Learning (aMCL) algorithm on several benchmark datasets from the UCI Machine Learning Repository. This is a standard practice to demonstrate the generalizability and effectiveness of a machine learning model. The results would probably show a comparison of aMCL against standard approaches like vanilla MCL and Relaxed WTA, possibly including other relevant baselines. Key metrics would include error measures such as mean squared error (MSE) or root mean squared error (RMSE), and other measures relevant to the quality of the predictions. Statistical significance testing is crucial here to ensure observed improvements are not due to chance. A strong performance on a variety of UCI tasks would be a significant finding, supporting the robustness and broad applicability of the aMCL algorithm over existing MCL methods. The analysis should carefully address the limitations of the UCI datasets and acknowledge that favorable results on these datasets alone don’t guarantee real-world success.
Future Works#
The authors suggest several avenues for future research. Improving the temperature schedule is crucial, as it significantly impacts performance. Developing methods to automatically determine optimal schedules would enhance usability and efficiency. A more in-depth analysis of the algorithm’s convergence properties, particularly under finite temperature conditions, is also warranted. Exploring the impact of the scheduler’s decay speed on phase transitions warrants further investigation. Extending the theoretical analysis to cover a wider range of loss functions beyond the Euclidean distance, and investigating the generalization capabilities of aMCL on out-of-distribution samples are important considerations. Finally, research into stochastic simulated annealing for aMCL could improve its robustness and exploration capabilities, and studying the algorithm’s scalability for high-dimensional data and complex problems is another key area for future work.
More visual insights#
More on figures
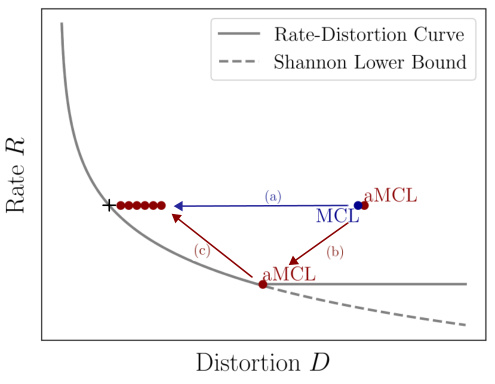
This figure shows how the training process of MCL and aMCL affects the rate-distortion curve. The rate-distortion curve represents the trade-off between the rate (number of bits used to represent the data) and the distortion (difference between the original and compressed data). MCL tends to converge towards a local minimum on this curve while aMCL, using simulated annealing, explores more of the curve, leading to a potentially better overall performance. The optimal distortion corresponds to the point where the rate is equal to log2(n), where n is the number of hypotheses.
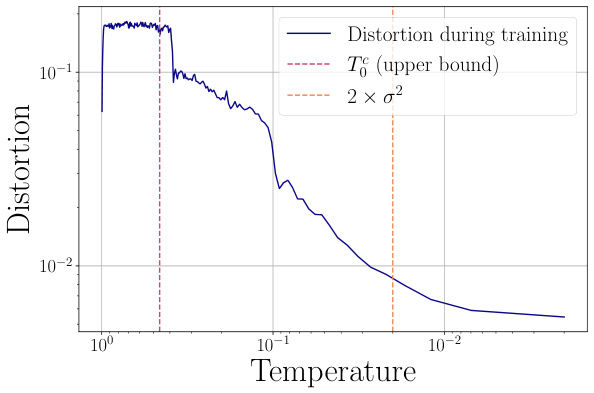
This figure shows the relationship between distortion and temperature during the training process. The training starts with high temperature and the model predicts the conditional mean. Then there is a plateau phase. As the temperature decreases below T₀, the model transitions to a different phase and the predictions move towards the barycenter of the Gaussian, then they split, causing another transition.

This figure compares the performance of three different methods for multiple choice learning on a mixture of three Gaussians dataset. It shows that the Winner-Takes-All (WTA) approach in standard MCL leads to some hypotheses being unused and higher quantization error, while the Relaxed-WTA approach biases predictions towards the distribution’s center. Annealed MCL addresses these issues by using simulated annealing, resulting in better coverage of the hypothesis space and improved robustness.

This figure compares the performance of three different methods for multiple choice learning: MCL, Relaxed WTA, and Annealed MCL. It shows that Annealed MCL overcomes the limitations of the other two methods by achieving a lower quantization error and avoiding bias toward the distribution’s barycenter. The visualization uses a mixture of three Gaussian distributions to illustrate the differences in prediction accuracy and hypothesis diversity.

This figure compares the performance of three different methods for ambiguous prediction tasks: MCL, Relaxed WTA, and Annealed MCL. It uses a Mixture of three Gaussians as a test case. The visualizations show that standard MCL suffers from hypothesis collapse (unused hypotheses). Relaxed WTA shows a bias towards the center of the distribution. Annealed MCL offers improved performance and handles the ambiguity of the data more effectively by utilizing annealing.
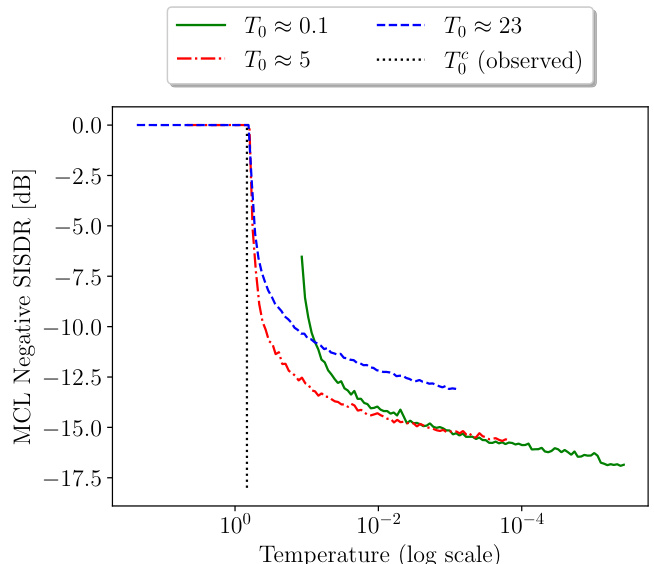
This figure shows the impact of the initial temperature (T₀) on the training trajectory of Annealed Multiple Choice Learning (aMCL) for speech separation. The plot displays the negative MCL SI-SDR (a measure of separation quality) against the temperature on a logarithmic scale. Different initial temperatures (T₀ ≈ 0.1, T₀ ≈ 5, and T₀ ≈ 23) result in distinct curves. A lower score indicates better performance. The figure demonstrates the ‘phase transition’ phenomenon of aMCL where the loss initially plateaus before decreasing sharply at a critical temperature.
More on tables
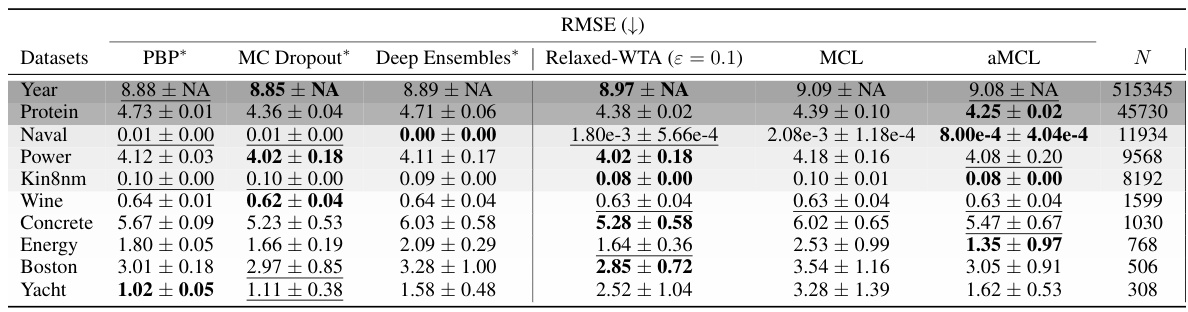
This table compares the Root Mean Squared Error (RMSE) achieved by different regression models on several UCI datasets. The models compared include PBP, MC Dropout, Deep Ensembles (all from prior work), Relaxed-WTA (a variant of the proposed method), standard MCL, and the proposed aMCL. The table shows that aMCL generally achieves comparable or better performance than other methods.

This table presents the results of a source separation experiment using four different methods: PIT, MCL, aMCL, and Relaxed-WTA. The experiment was conducted on the WSJ0-mix dataset with 2 and 3 speakers. The results are reported as the mean and standard deviation of the PIT SI-SDR (Scale-Invariant Signal-to-Distortion Ratio) metric over three different training seeds. The PIT SI-SDR is a measure of the quality of source separation, with higher values indicating better performance. The table shows that the performance of aMCL is comparable to PIT and better than MCL and Relaxed-WTA.

This table compares the Root Mean Squared Error (RMSE) of different methods on UCI regression benchmark datasets. It includes the proposed Annealed Multiple Choice Learning (aMCL) method and several baselines (Probabilistic Backpropagation, Monte Carlo Dropout, Deep Ensembles, Relaxed-WTA, and MCL). The results show how aMCL compares to the baselines in terms of RMSE and indicates whether aMCL outperforms or performs comparably to existing methods.

This table presents the results of the UCI regression benchmark experiments comparing different methods in terms of Distortion. It shows the performance of MCL, aMCL, and Relaxed-WTA (with epsilon = 0.1) across several datasets. The rows are sorted by dataset size. Best and second-best results are highlighted.
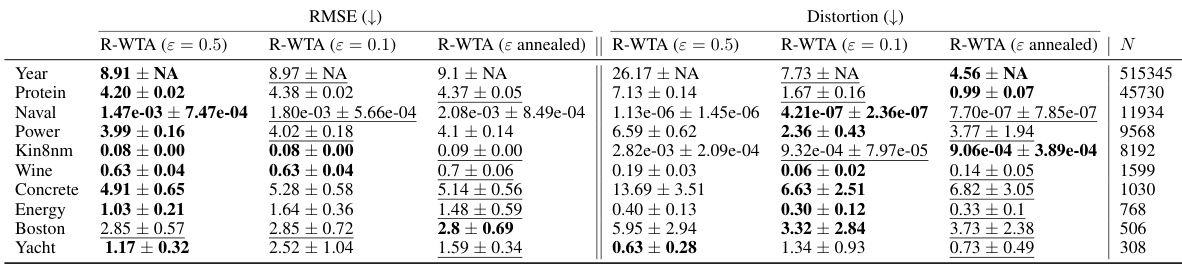
This table compares the performance of Relaxed-WTA with different values of epsilon (ε) on UCI regression datasets. It shows RMSE and Distortion metrics for Relaxed-WTA with fixed ε values (0.5, 0.1) and an annealed ε, demonstrating how the choice of ε impacts performance, and indicating that a lower or annealed ε generally produces better results for the Distortion metric.
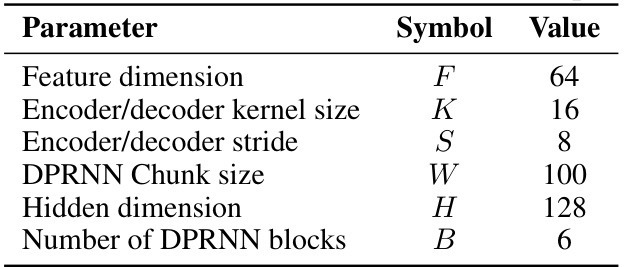
This table shows the hyperparameters used for the DPRNN model in the speech separation experiments. It lists the values for parameters such as feature dimension, encoder/decoder kernel size, stride, DPRNN chunk size, hidden dimension, and the number of DPRNN blocks.
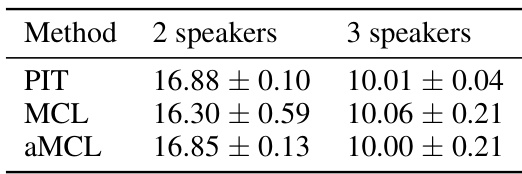
This table presents the results of a source separation experiment using four different methods: PIT, MCL, aMCL, and Relaxed-WTA. The experiment was conducted on the WSJ0-mix evaluation set, with separate results for 2-speaker and 3-speaker scenarios. The results are the mean and standard deviation of the PIT SI-SDR (Scale-Invariant Signal-to-Distortion Ratio) metric, averaged across three independent training runs.
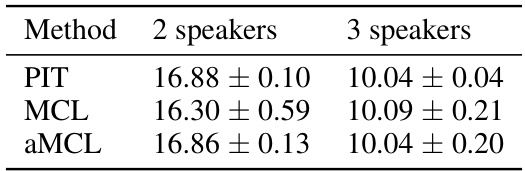
This table compares the performance of three different methods for speech separation: PIT, MCL, and aMCL. It shows the average PIT and MCL SI-SDR scores for 2-speaker and 3-speaker scenarios, along with standard deviations across three training runs. The results highlight the performance of each method and their relative robustness to initial conditions.
Full paper#