↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Stochastic optimal control is challenging, especially in high-dimensional systems. Existing methods, often based on iterative diffusion optimization (IDO), suffer from high error rates due to the non-convexity of the loss landscape and the difficulty of computing gradients through complex stochastic processes. These limitations hinder accurate control of noisy dynamical systems across various applications.
This paper introduces Stochastic Optimal Control Matching (SOCM), a novel IDO algorithm. SOCM addresses the challenges by learning the control function via a least squares problem, aiming to fit a matching vector field. A key innovation is the path-wise reparameterization trick, efficiently estimating gradients without relying on computationally expensive adjoint methods. Experimental results demonstrate SOCM’s superiority over existing IDO techniques, achieving substantially lower errors in several control problems.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in stochastic optimal control and machine learning. It introduces a novel algorithm that significantly improves the accuracy of existing methods, especially in high-dimensional settings. The path-wise reparameterization trick and the bias-variance decomposition are valuable contributions with broader applications. This work opens up new avenues for research in generative models and CNFs, especially those involving high-dimensional vector fields.
Visual Insights#

This figure compares the performance of three stochastic optimal control algorithms (Adjoint, SOCM, and Cross-entropy) across different dimensions in estimating the control objective, which ideally should be zero. The y-axis shows the control objective estimate, and the x-axis represents the dimensionality of the problem. Error bars indicate standard deviations. Noticeably, the Cross-entropy method performs significantly worse than the others in higher dimensions.

This table presents the average time taken per iteration for different stochastic optimal control algorithms, namely SOCM, SOCM with constant matrices Mt = I, SOCM-Adjoint, Adjoint, Cross-entropy, Log-variance, Moment, and Variance. The results are based on the QUADRATIC OU (EASY) experiments, as shown in Figure 2 of the paper, and are obtained using an exponential moving average with a coefficient of 0.01 to smooth out the data. The algorithms are implemented using a 16GB V100 GPU.
In-depth insights#
SOCM Algorithm#
The Stochastic Optimal Control Matching (SOCM) algorithm is a novel technique for solving stochastic optimal control problems. It leverages the path-wise reparameterization trick, a key innovation, to efficiently estimate gradients of conditional expectations, a challenge in existing IDO (Iterative Diffusion Optimization) methods. SOCM frames the problem as a least squares regression, fitting a matching vector field. The optimization simultaneously considers both the control function and a set of reparameterization matrices, effectively minimizing the variance of the matching vector field and leading to more stable training and superior performance compared to existing IDO techniques. Experimental results demonstrate SOCM’s effectiveness across diverse control problems, achieving lower error in some cases by an order of magnitude, highlighting the algorithm’s robustness and potential for broad applicability in science and engineering.
Pathwise Reparameterization#
Pathwise reparameterization is a novel technique introduced for efficiently estimating gradients of expectations involving functionals of stochastic processes. Its core innovation lies in cleverly manipulating the dependence of these functionals on initial conditions, allowing for effective gradient calculations. This contrasts with traditional adjoint methods which often involve solving computationally expensive ODEs or PDEs. The technique is particularly valuable in high-dimensional stochastic optimal control problems, where gradient estimation is notoriously challenging due to the variance of the importance weights and the complexity of the associated dynamics. The authors demonstrate that it significantly improves the stability and accuracy of stochastic optimal control training, leading to substantially lower errors than existing methods in several benchmark problems. The pathwise reparameterization trick enables a novel algorithm, SOCM, which learns a control by fitting a matching vector field, further enhancing performance and efficiency.
Bias-Variance Tradeoff#
The bias-variance tradeoff is a central concept in machine learning, representing the tension between model accuracy and its sensitivity to training data variations. High bias implies the model is too simplistic, underfitting the data and missing crucial relationships. This results in consistent but inaccurate predictions across different datasets. High variance, on the other hand, signifies an overly complex model, overfitting the training data and capturing noise instead of underlying patterns. This leads to highly variable performance, excellent accuracy on training data but poor generalization to unseen examples. The optimal model balances these, minimizing error by finding a sweet spot where the model captures essential patterns without being overly sensitive to data noise. Techniques like regularization and cross-validation help manage this tradeoff by controlling model complexity and evaluating performance on independent datasets.
Experimental Results#
The ‘Experimental Results’ section of a research paper is crucial for validating the claims made in the introduction and demonstrating the effectiveness of the proposed methodology. A strong ‘Experimental Results’ section should go beyond merely presenting numerical results; it should provide a thorough analysis of the data, comparing different approaches, highlighting the significance of findings, and acknowledging any limitations. Clear visualizations like graphs and tables are essential for effective communication. Statistical significance tests are necessary to ensure results are not due to chance. The section should also include details about the experimental setup, ensuring the reproducibility of the results. Comparisons with existing state-of-the-art methods are vital to demonstrate novelty and improvement. Addressing potential confounding factors is crucial for ensuring the reliability of the reported results. Lastly, the discussion of results should focus on interpreting the findings and their implications for the wider research community. A thoughtful presentation of experimental results is what distinguishes a high-quality research paper from a merely descriptive one.
Future Research#
Future research directions stemming from this Stochastic Optimal Control Matching (SOCM) work could explore several promising avenues. Extending SOCM to handle high-dimensional, complex systems is crucial, potentially investigating more sophisticated neural network architectures or alternative function approximation methods to manage the increased computational demands and mitigate the variance issues encountered in such scenarios. Improving the efficiency of the path-wise reparameterization trick is another key area, seeking to reduce its computational cost without sacrificing accuracy or stability. This could involve exploring novel algorithmic approaches or alternative gradient estimation techniques. Investigating the relationship between SOCM and other generative models, particularly those based on score matching and diffusion processes, warrants deeper study. The inherent connection suggests the potential for cross-pollination of ideas and methods, potentially leading to more robust and efficient generative modeling techniques. Finally, applying SOCM to diverse real-world problems in robotics, finance, or materials science could showcase its practical impact and illuminate further avenues of research based on empirical observations and application-specific challenges.
More visual insights#
More on figures
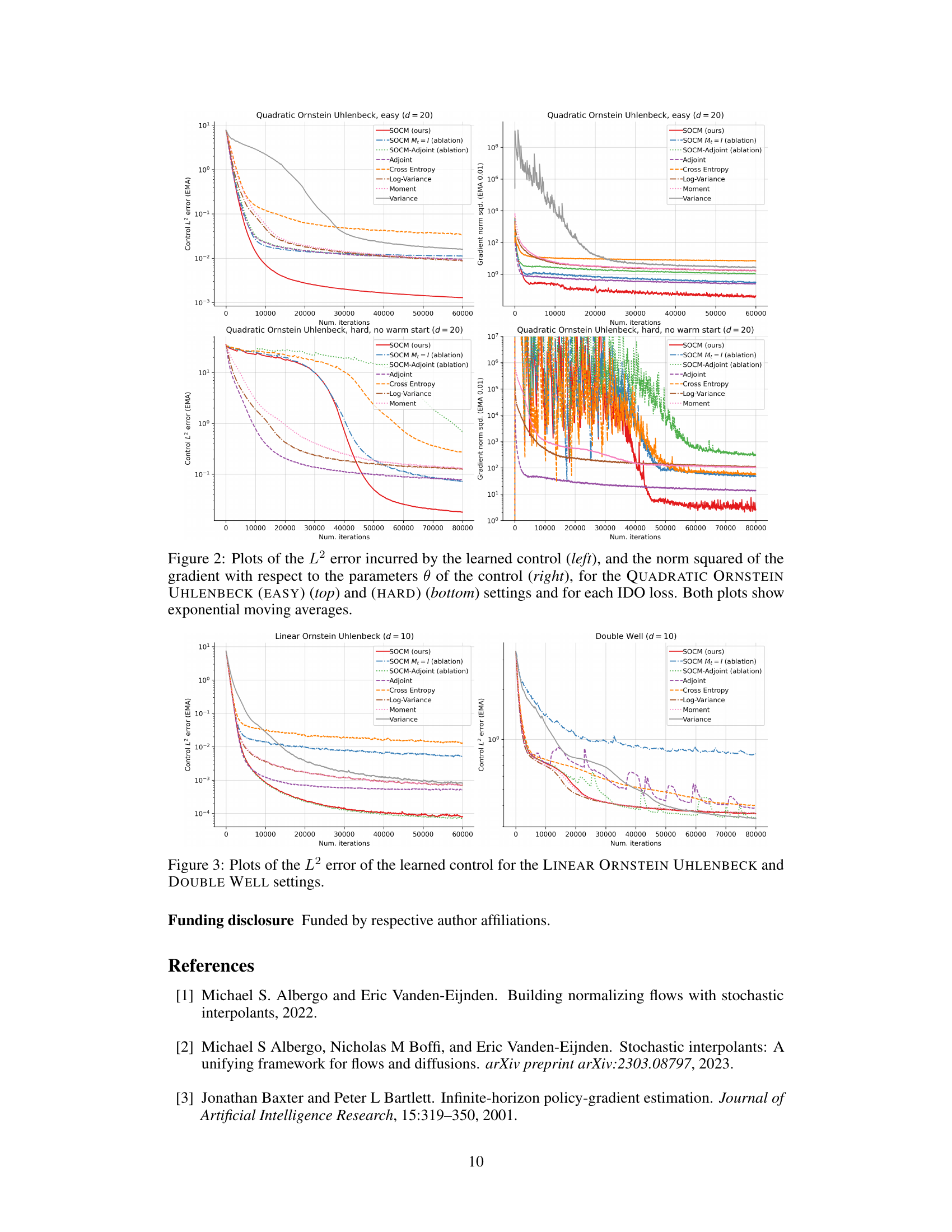
This figure compares the performance of different iterative diffusion optimization (IDO) algorithms for stochastic optimal control. The left plots show the L2 error between the learned control and the ground truth control. The right plots show the squared norm of the gradient of the loss function with respect to the control parameters. The results are shown for two settings: QUADRATIC ORNSTEIN UHLENBECK (EASY) and QUADRATIC ORNSTEIN UHLENBECK (HARD). Exponential moving averages are used to smooth the data.

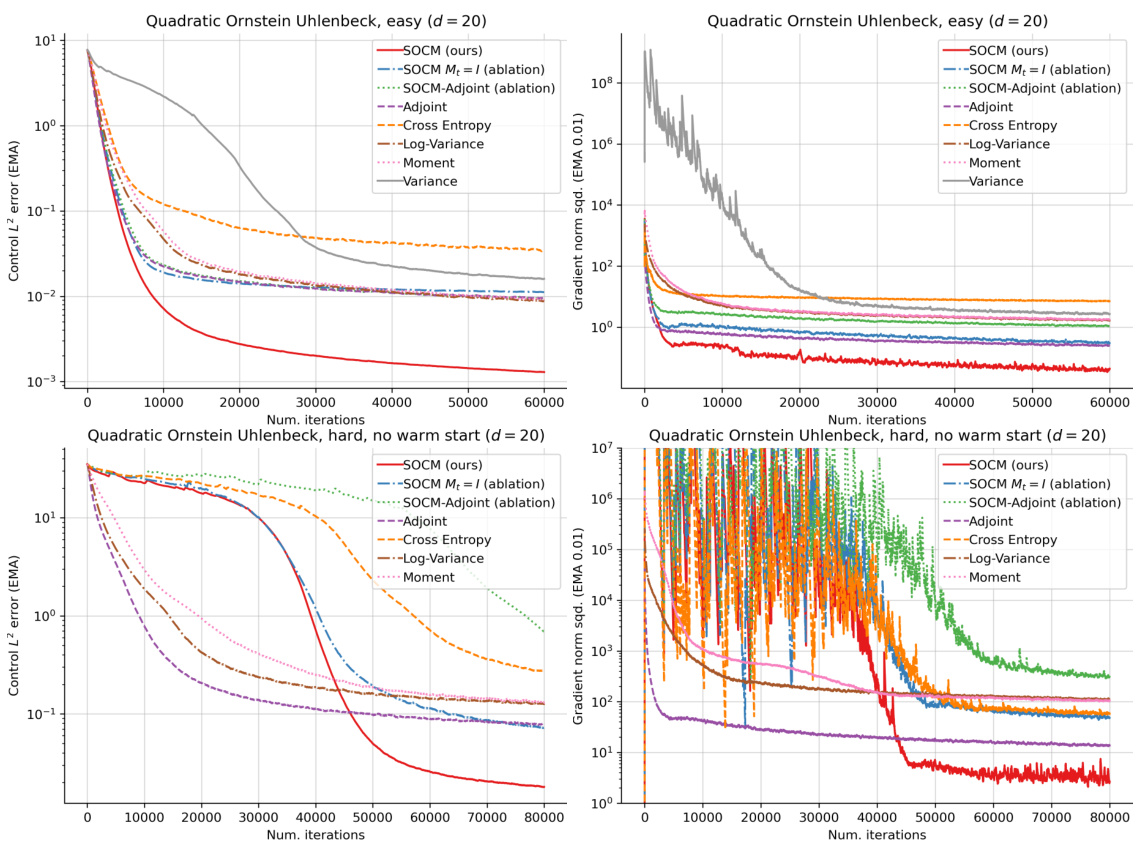
This figure presents plots showing the L2 error of the learned control for two different control problems: LINEAR ORNSTEIN UHLENBECK and DOUBLE WELL. The plots display the L2 error (a measure of how close the learned control is to the optimal control) over the number of training iterations. Each line on the plot represents a different algorithm used to learn the control. The plot allows for a comparison of the performance of different algorithms in high dimensional stochastic optimal control problems. The DOUBLE WELL problem is particularly interesting as it involves a multimodal solution.
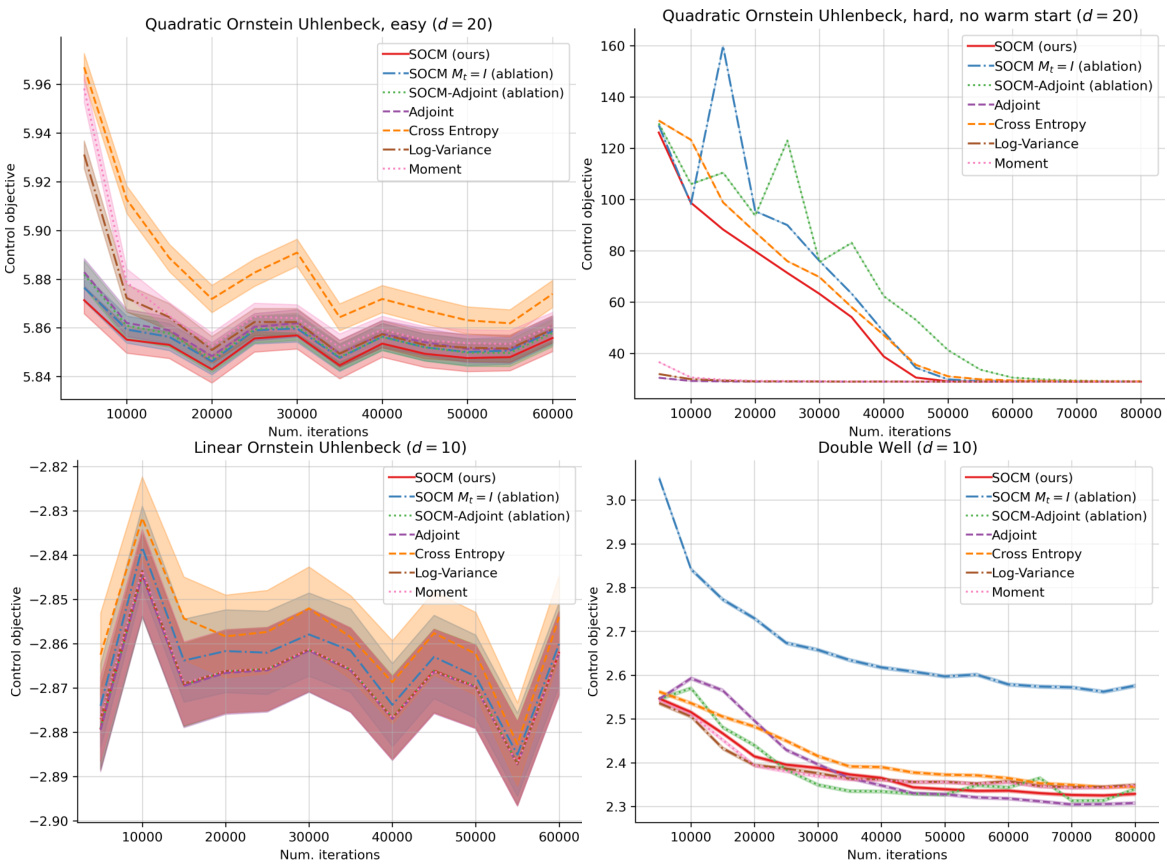
This figure presents the control objective for four different experimental settings: Quadratic Ornstein Uhlenbeck (easy), Quadratic Ornstein Uhlenbeck (hard), Linear Ornstein Uhlenbeck, and Double Well. Each setting’s plot shows the control objective over the course of training for several different algorithms, including the authors’ proposed SOCM method and various comparative algorithms. The plots illustrate the performance of each algorithm in terms of minimizing the control objective over time. Error bars indicating standard deviation are shown for some of the plots, giving an estimate of confidence intervals for the control objective estimations.

This figure presents plots illustrating the normalized standard deviation of the importance weights (√Var[α(u, Xu, B)]/E[α(u, Xu, B)]) across four different experimental settings: Quadratic Ornstein Uhlenbeck (easy), Quadratic Ornstein Uhlenbeck (hard), Linear Ornstein Uhlenbeck, and Double Well. The plots show this metric as a function of the number of iterations for several different stochastic optimal control algorithms (SOCM, SOCM with constant Mt = I, SOCM-Adjoint, Adjoint, Cross-Entropy, Log-Variance, Moment, and Variance). The normalized standard deviation of α serves as an indicator of the learned control’s proximity to the optimal control; a value of zero indicates optimality. The plots reveal the performance of each algorithm in terms of minimizing the variance of the importance weight, offering insights into their efficiency and stability during training.

This figure compares the norm squared of the gradient for different stochastic optimal control algorithms across two distinct problem settings: Linear Ornstein Uhlenbeck and Double Well. The plots showcase the gradient magnitude over the course of the training iterations for each algorithm. The aim is to illustrate the stability and efficiency of the gradient calculations for each method. The lower the gradient norm, the smoother the optimization landscape and potentially the more efficient the training process.
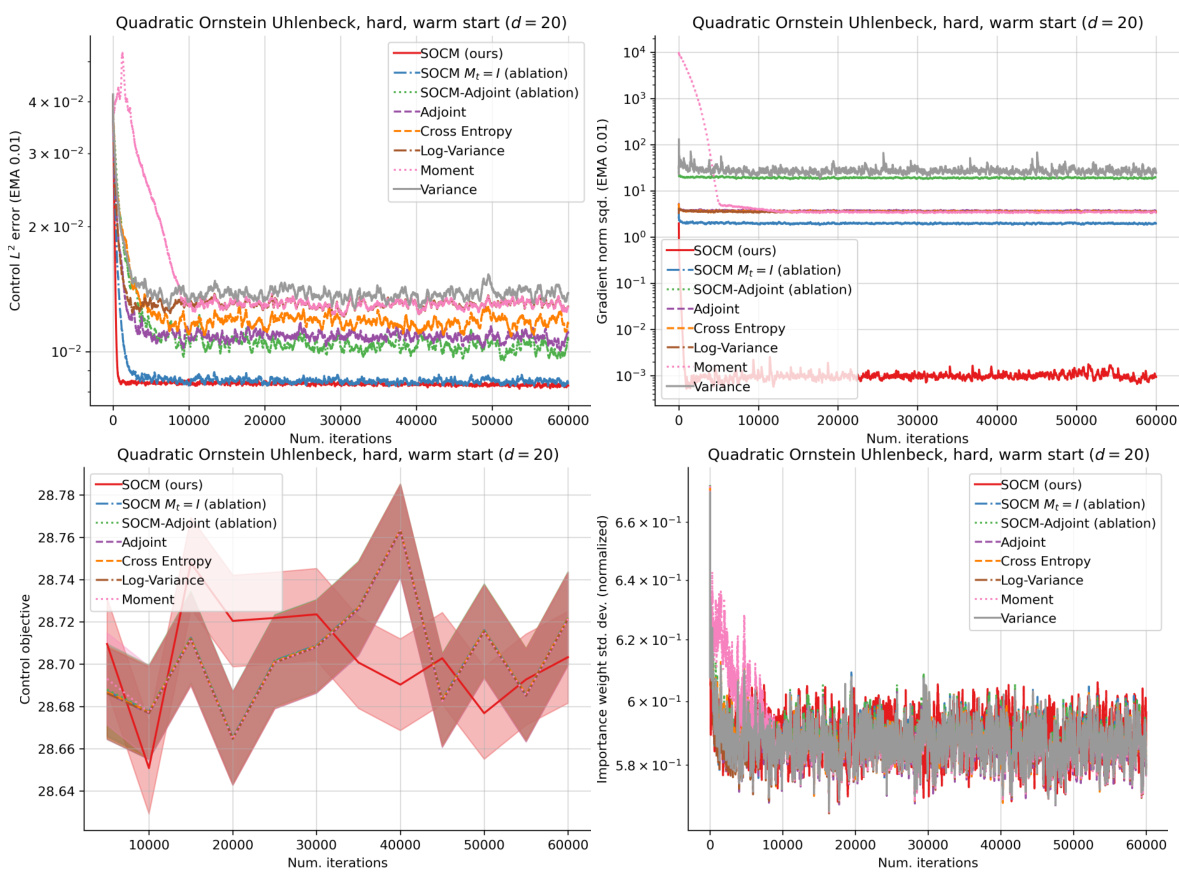
This figure presents the results of the QUADRATIC ORNSTEIN-UHLENBECK (HARD) experiment, showing the performance of SOCM and other IDO techniques without warm-starting. The plots display the exponential moving averages (EMA) of the L2 error of the learned control, the norm squared of the gradients, and the control objective over the course of training iterations. The plots illustrate the comparative performance across different methods and highlight the effectiveness of SOCM in achieving lower error and variance.
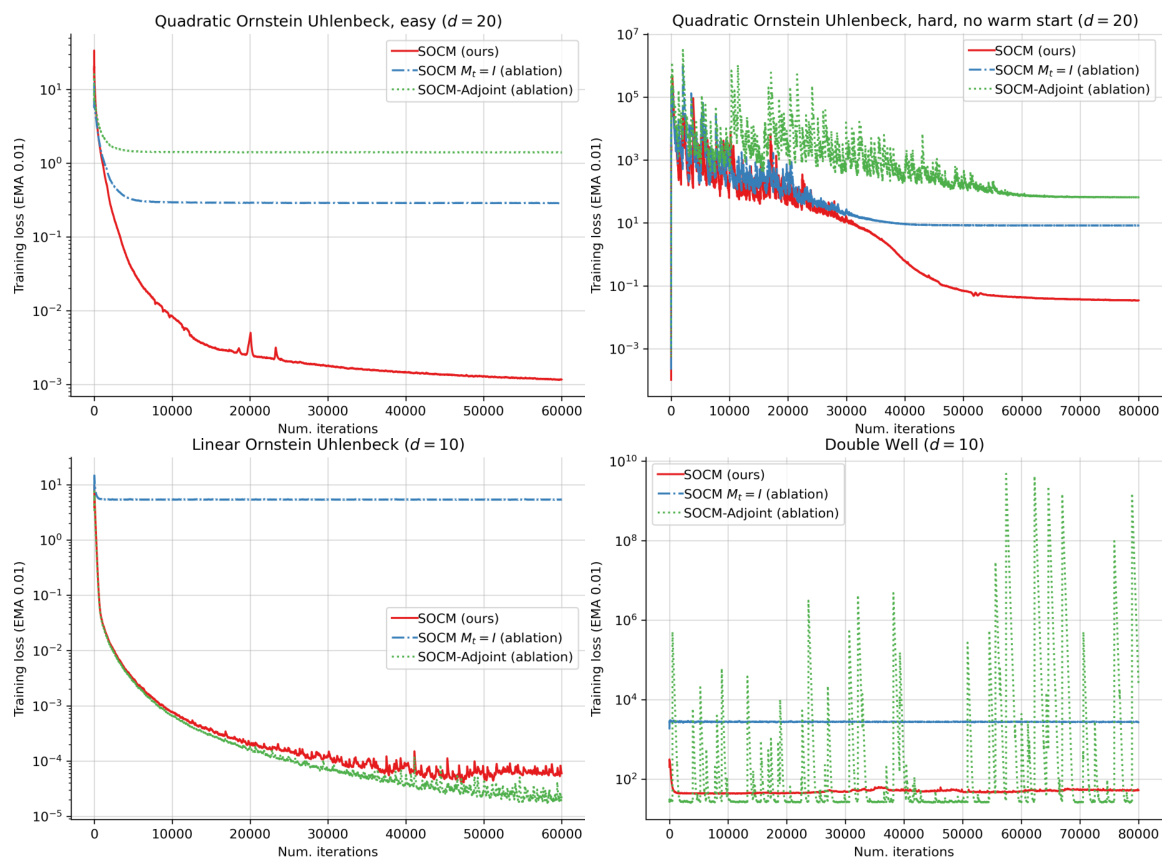
This figure presents plots of the training loss for three different stochastic optimal control algorithms: SOCM, SOCM with constant reparameterization matrices (Mt = I), and SOCM-Adjoint. The training loss is shown for four different control problems: Quadratic Ornstein Uhlenbeck (easy), Quadratic Ornstein Uhlenbeck (hard), Linear Ornstein Uhlenbeck, and Double Well. The plots show how the training loss decreases over the number of iterations for each algorithm and control problem. The plots illustrate the effect of using different loss functions and reparameterization methods on the overall performance of each algorithm.

This figure shows the control L2 error and the gradient norm squared for the adjoint method applied to the DOUBLE WELL problem, using two different Adam learning rates (3e-5 and 1e-4). The plots demonstrate that the instabilities observed in the adjoint method are not resolved even when using smaller learning rates, suggesting a fundamental problem within the loss function itself.
Full paper#