Diffusion Models are Certifiably Robust Classifiers

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it provides a much-needed theoretical foundation for the robustness of diffusion classifiers, a rapidly growing area of research. Its findings challenge existing assumptions about the limits of diffusion models and open new avenues for improving their robustness, making it highly relevant to researchers in machine learning, computer vision, and AI safety.

Visual Insights

#

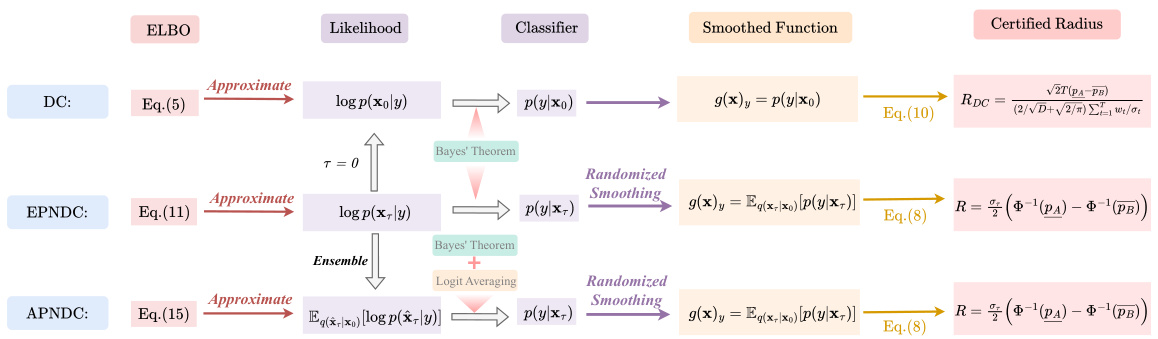
This figure illustrates the paper’s main contributions: deriving the Lipschitz constant and certified robustness for diffusion classifiers, introducing novel evidence lower bounds to approximate log-likelihood, constructing classifiers using Bayes’ theorem, and applying randomized smoothing to derive tighter certified robust radii. It visually depicts the relationships and processes involved in each step.

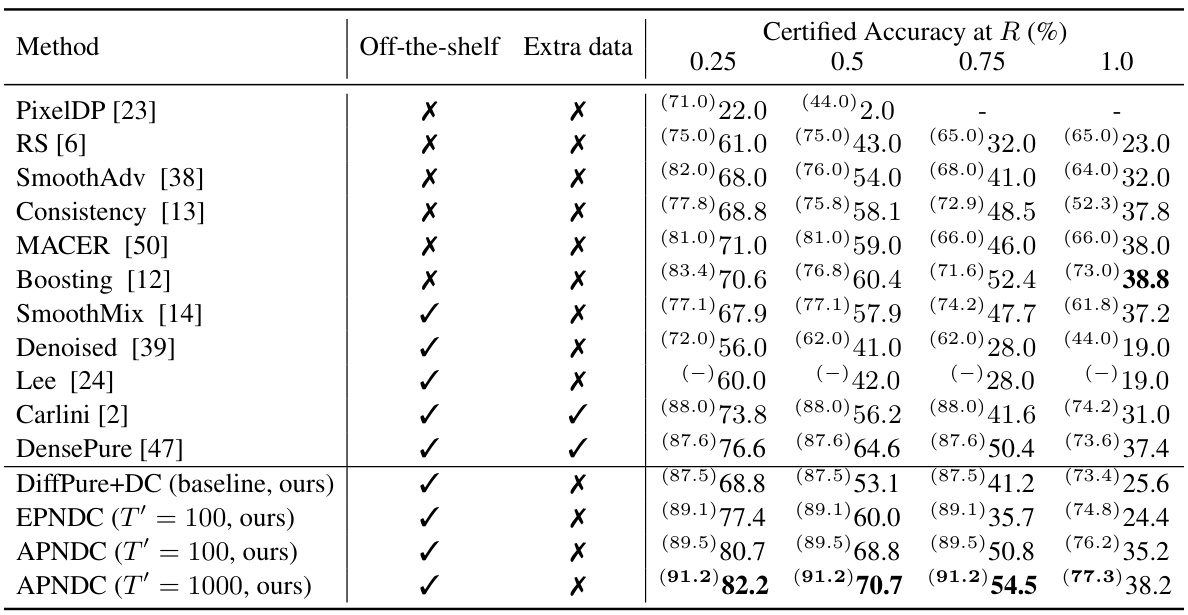
This table presents the certified accuracy of various methods on the CIFAR-10 test set under different l2 perturbation radii (0.25, 0.5, 0.75, 1.0). The clean accuracy (accuracy on unperturbed data) is shown in parentheses for each method. The results from Xiao et al. [47] are included for comparison. Note that Carlini et al. [2] and Xiao et al. [47] used additional ImageNet-21k data for training, unlike the methods presented in this paper which only use a single off-the-shelf diffusion model.

In-depth insights

#

Diffusion Robustness

#

The concept of “Diffusion Robustness” in the context of machine learning models, specifically those based on diffusion processes, is a fascinating area of research. It explores how the inherent properties of diffusion models, which excel at modeling complex data distributions, contribute to their robustness against adversarial attacks and out-of-distribution data. A key aspect is the smoothness of the learned representations, which implies that small input perturbations lead to relatively small changes in the model’s output. This smoothness can be quantified through the Lipschitz constant of the model, allowing for the establishment of certified robustness bounds. This means we can mathematically guarantee the model’s accuracy within a certain perturbation radius. However, achieving tight certified robustness bounds remains a challenge, with much of the research focusing on methods to reduce the Lipschitz constant and refining the classification process, often by incorporating noise explicitly into the input data or generalizing the models to handle Gaussian-corrupted inputs. The successful application of this concept to generate certifiably robust classifiers opens up many exciting possibilities for developing reliable AI systems in safety-critical applications.

Noised Diffusion

#

The concept of ‘Noised Diffusion’ likely refers to a modification of standard diffusion models, which are known for their ability to generate high-quality samples by gradually removing noise from random data. Adding noise to the input data before processing with a diffusion model, as implied by the term, could be a technique to improve robustness or to enhance certain properties of the generated samples. This addition of noise could serve several purposes, including regularization, making the model less sensitive to minor variations in the input and thus more robust to adversarial examples. Noise could also improve exploration of the data space, helping the model learn more intricate features or prevent overfitting to specific training examples. However, the exact implementation details of this technique would determine its effect on the model and the resulting output and may require careful tuning of the added noise level and distribution. The effectiveness of ‘Noised Diffusion’ would depend highly on the specific application, the type of noise used, and the architecture of the diffusion model itself.

Certified Robustness

#

The concept of “Certified Robustness” in the context of machine learning models, particularly classifiers, is crucial for building trustworthy AI systems. It signifies the ability to mathematically guarantee a model’s resilience against adversarial attacks within a specified radius. This is a significant advancement over empirical robustness testing, which only demonstrates performance on a limited set of attacks. Certified robustness provides provable guarantees, offering more confidence in the model’s reliability, especially in safety-critical applications. The methods for achieving certified robustness often involve techniques like randomized smoothing, which smooths the model’s decision boundary to enhance its stability against perturbations. However, achieving high certified robustness typically comes with trade-offs, such as increased computational costs or reduced accuracy. The exact balance between these factors is a subject of ongoing research, and different approaches to certified robustness offer varying degrees of this trade-off. Analyzing the Lipschitz constant of the classifier is key to understanding and improving its certified robustness, as it provides a bound on the model’s sensitivity to input changes. Ultimately, certified robustness aims to bridge the gap between theoretical understanding and real-world performance, paving the way for safer and more reliable AI deployments.

Complexity Reduced

#

The heading ‘Complexity Reduced’ in a research paper likely discusses techniques to optimize computational efficiency. This could involve algorithmic improvements, such as employing faster data structures or algorithms, or architectural modifications, like parallel processing or distributed computing. The paper might detail specific strategies used to decrease computational complexity, for example, variance reduction methods, which minimize the variability in calculations, leading to faster convergence or reduced sample sizes. Another approach might be approximation techniques, where precise but costly calculations are replaced by computationally cheaper estimates that still maintain sufficient accuracy. The paper likely also presents experimental results demonstrating the effectiveness of the proposed complexity reduction techniques, showcasing improvements in computational time without significantly compromising accuracy or performance. Trade-offs between complexity and accuracy are likely discussed, providing a nuanced understanding of the balance achieved. Ultimately, the section aims to illustrate that the research is not only theoretically sound but also practically feasible and scalable for real-world applications.

Future Works

#

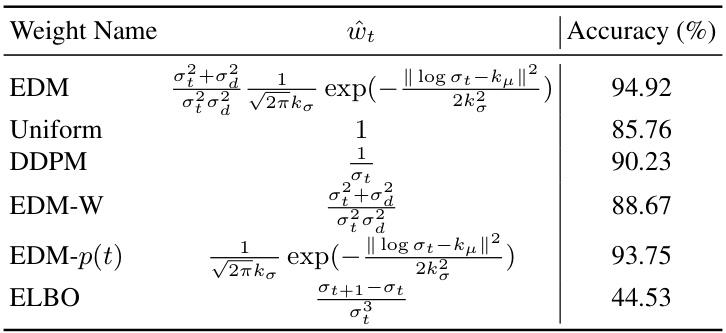
Future work could explore several promising avenues. Improving the tightness of certified robustness bounds is paramount; current methods, while demonstrating significant improvements, still yield conservative estimates. This necessitates further theoretical investigation into the Lipschitz constant of diffusion classifiers and exploring non-constant Lipschitzness techniques. Another crucial area is reducing the computational cost. The current approach, while enhanced, still remains computationally expensive for large-scale datasets like ImageNet. Strategies could include optimized algorithms or more efficient variance reduction techniques. Finally, extending the methodology to other generative models beyond diffusion models, such as GANs or VAEs, would broaden the applicability and impact of the certified robustness framework. Investigating the influence of different diffusion model architectures and hyperparameter settings on certified robustness is also a key area of future exploration.

More visual insights

#

More on tables

This table presents the certified accuracy of various methods on the CIFAR-10 test set under different l2 perturbation radii (0.25, 0.5, 0.75, 1.0). The clean accuracy (without perturbations) is shown in parentheses. It compares the performance of the proposed methods (EPNDC and APNDC) with existing state-of-the-art techniques for certified robustness. The table also indicates whether the methods used additional ImageNet-21k data for training.

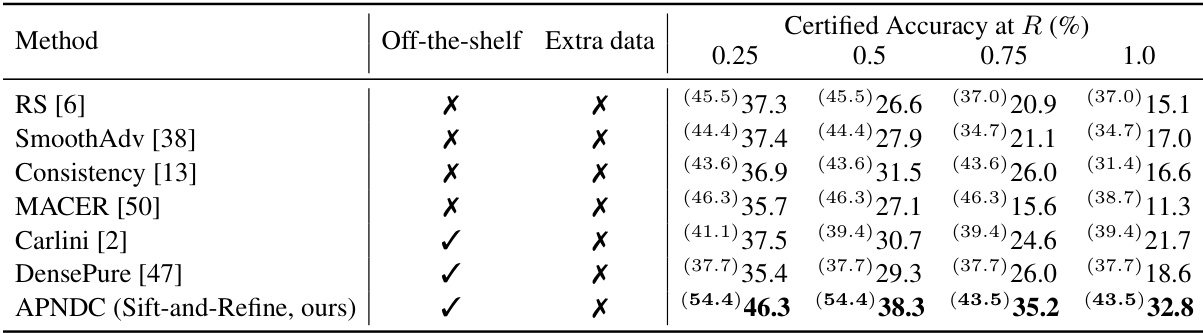
This table presents the certified accuracy of different methods on the ImageNet-64x64 dataset under various l2 perturbation radii (0.25, 0.5, 0.75, 1.0). The clean accuracy (accuracy without adversarial attacks) is shown in parentheses for each method. It compares the performance of the proposed APNDC method (with Sift-and-Refine) against several existing state-of-the-art methods. The ‘Off-the-shelf’ column indicates whether the method uses a pre-trained model without additional training, and the ‘Extra data’ column notes whether extra data (beyond the ImageNet-64x64 training set) was used. The results highlight the superior certified robustness of the APNDC method, particularly when no extra data is used.

This table presents the certified accuracy of various methods on the CIFAR-10 test set under different l2 perturbation radii (0.25, 0.5, 0.75, and 1.0). The clean accuracy (accuracy on unperturbed images) is shown in parentheses for each method. It compares the performance of the proposed methods (DiffPure+DC, EPNDC, APNDC) against existing state-of-the-art methods for certified robustness. Note that Carlini et al. [2] and Xiao et al. [47] used extra ImageNet-21k data for training, while the proposed methods use only a single off-the-shelf diffusion model without any additional data.

This table presents the certified accuracy results on the CIFAR-10 test set for various certified robustness methods. The table shows the certified accuracy (%) at different l2 radii (0.25, 0.5, 0.75, 1.0) for each method. Clean accuracy (in parentheses) indicates the model’s performance on unperturbed data. Methods using extra ImageNet-21k data are noted. The results for Xiao et al. [47] are replicated here for comparison.

This table presents the certified accuracy results on the CIFAR-10 test set for various certified robustness methods at different perturbation radii (l2 norm). The table compares the performance of several methods, including some baselines from previous works, and highlights the superior performance of the proposed methods (EPNDC and APNDC). The ‘Off-the-shelf’ column indicates whether a pre-trained model was used without any additional training or fine-tuning, and the ‘Extra data’ column shows if additional datasets were used for training or other improvements. Clean accuracy (accuracy without adversarial attacks) is shown in parentheses for each method.

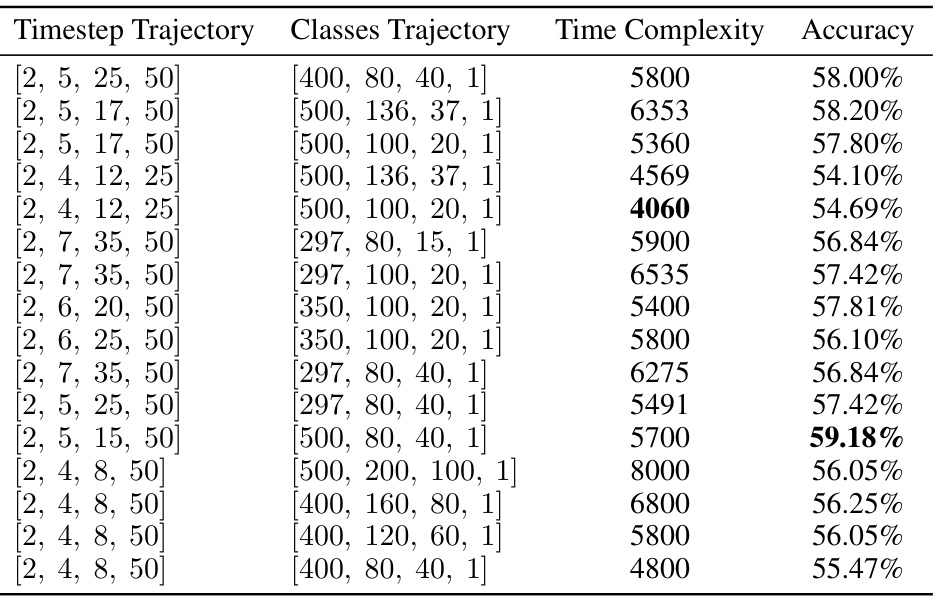
This table presents the certified accuracy results on the CIFAR-10 dataset for various methods, including the proposed approach (APNDC). The results are shown for different l2 perturbation radii (0.25, 0.5, 0.75, 1.0). The clean accuracy (accuracy on unperturbed images) is also included for each method in parentheses. The table allows for a comparison of the certified robustness of the proposed methods against existing state-of-the-art techniques, highlighting their superior performance, especially when no additional data is used.

Full paper

#