Provable and Efficient Dataset Distillation for Kernel Ridge Regression

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it offers a novel, theoretically grounded approach to dataset distillation for kernel ridge regression. This significantly reduces computational costs and improves data quality, which are critical issues in deep learning. It also opens up new avenues for research in dataset distillation, including the theoretical analysis of algorithms and privacy-preserving techniques.

Visual Insights

#

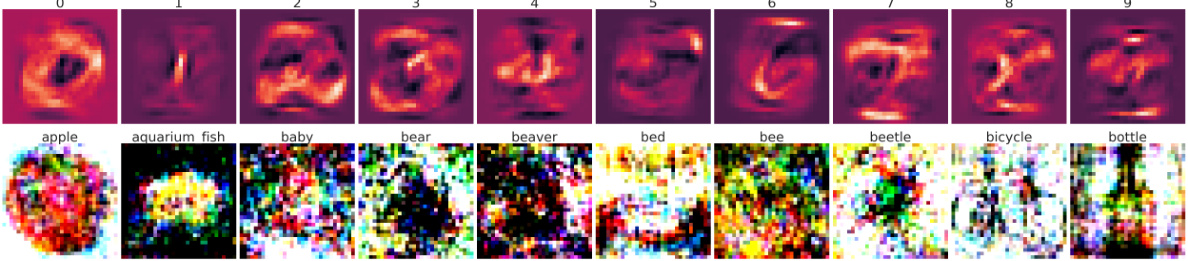
This figure shows the distilled data generated for MNIST and CIFAR-100 datasets using Linear Ridge Regression (LRR). The top row displays the distilled MNIST data (one image per class), and the bottom row presents the distilled CIFAR-100 data (one image per class). The caption highlights a key finding from Theorem 4.1: a smaller regularization parameter (λs) generally leads to better results when constructing distilled datasets.

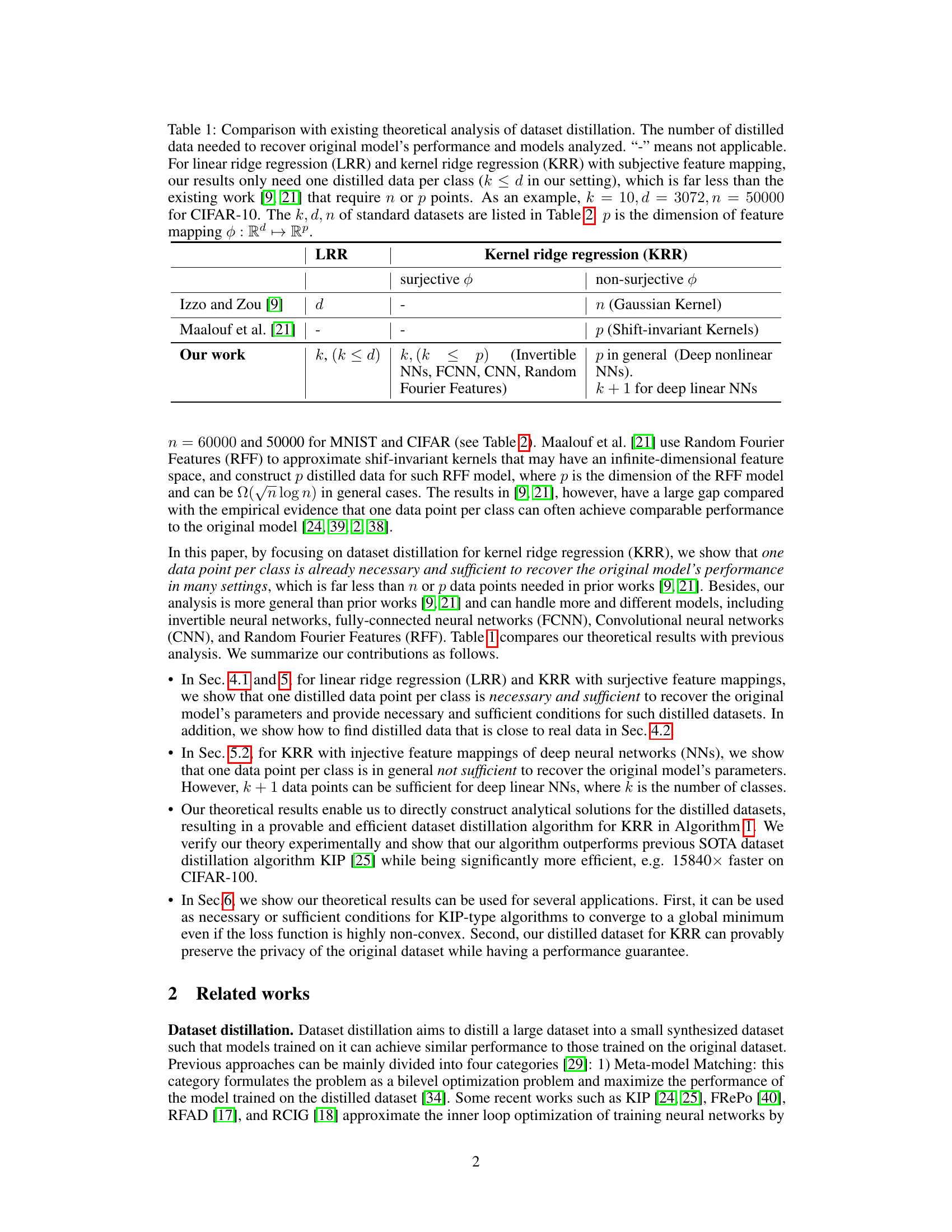
This table compares the number of distilled data points required by different theoretical analyses to recover the original model’s performance for various models. It highlights that the proposed method requires significantly fewer data points (k, where k is the number of classes) compared to existing work (n, the number of data points in the original dataset, or p, the dimensionality of the feature mapping).

In-depth insights

#

KRR Distillation

#

Kernel Ridge Regression (KRR) distillation focuses on efficiently creating a smaller, synthesized dataset that retains the performance of the original large dataset when training KRR models. The core idea is to reduce computational costs and improve data quality by working with a more manageable dataset. This technique involves finding a smaller representation of the original data that captures the essential information needed to make accurate predictions. The paper explores the theoretical underpinnings, establishing conditions for the distilled dataset to achieve similar performance. This is especially important for high-dimensional data such as images, where direct application of KRR can be computationally prohibitive. Provable and efficient algorithms are developed, and experiments demonstrate significant improvements in computational efficiency, often surpassing prior state-of-the-art methods by orders of magnitude, while maintaining comparable model accuracy. Furthermore, the distilled dataset offers potential privacy benefits as the original data cannot be fully reconstructed from the smaller, synthesized version.

Analytical Solutions

#

The concept of ‘Analytical Solutions’ within the context of a research paper likely refers to the derivation and presentation of mathematical formulas or algorithms that provide exact, closed-form solutions to a specific problem. This contrasts with numerical or approximate methods, which rely on iterative computations or heuristics. The value of analytical solutions lies in their precision and the potential for deeper theoretical understanding of the underlying phenomena. They offer insights into the relationships between variables and parameters, enabling researchers to explore the behavior of the system under various conditions without the limitations of computational cost or convergence issues often associated with numerical techniques. A well-developed analytical solution section would demonstrate the derivation of the formulas, rigorously validate their correctness, and discuss their limitations and applicability. It would also ideally compare the analytical solution to existing approaches or empirical observations, highlighting its advantages and disadvantages. The presence of analytical solutions elevates the theoretical rigor of the research and provides a foundation for further investigations.

Deep NN Distillation

#

Deep neural network (DNN) distillation, a crucial technique in model compression, focuses on transferring knowledge from a large, complex DNN to a smaller, more efficient one. The core idea is to retain the accuracy of the larger model while significantly reducing computational cost and resource consumption. This is achieved by training the smaller model (the student) to mimic the behavior of the larger model (the teacher), often using the teacher’s outputs or intermediate representations as supervisory signals. Different distillation methods employ various techniques to transfer knowledge effectively, such as mimicking class probabilities, feature maps, or intermediate layer activations. The effectiveness of the distillation process depends on several factors including the architecture of both teacher and student networks, the choice of knowledge transfer mechanism, and the training strategy. Successful DNN distillation results in a student network that achieves comparable performance to the teacher, but with greatly reduced model size and computational demands, thus making DNNs more deployable on resource-constrained devices. A key challenge is to design effective knowledge transfer mechanisms that capture the essential information from the teacher while avoiding overfitting or underfitting in the student network. Research in this area continues to explore new architectures, loss functions, and training procedures to improve the efficiency and accuracy of DNN distillation.

KIP Algorithm

#

The KIP algorithm, a prominent method in dataset distillation, focuses on meta-model matching, aiming to synthesize a smaller dataset that achieves comparable performance to the original, larger one. It tackles this by approximating the inner loop optimization of training neural networks, a computationally expensive process. The core idea is to find a distilled dataset that causes a similar model trained on it to achieve similar results to a model trained on the original dataset. Kernel methods are often used in KIP due to their efficacy in capturing high-level features. However, a key limitation is its computational cost, especially for large datasets. The method’s effectiveness significantly depends on its initialization and hyperparameter tuning, which can require substantial computational resources. Despite this limitation, KIP has shown promising empirical results; therefore, further research is needed for improved efficiency and theoretical understanding. Provable convergence and the impact of hyperparameters would improve the methodology significantly.

Privacy Analysis

#

A thorough privacy analysis of a dataset distillation method requires careful consideration of several key aspects. First, the definition of privacy needs to be explicitly stated; is it differential privacy, k-anonymity, or another metric? The choice impacts the techniques and guarantees. Second, the analysis should account for the entire data lifecycle; from data collection and preprocessing to model training and deployment. This means examining potential vulnerabilities at each stage. Third, the specific algorithm used for dataset distillation must be scrutinized; some techniques inherently offer better privacy preservation than others. For example, methods that focus solely on label distillation might leak sensitive information embedded in the data features. Fourth, the nature of the underlying data and its sensitivity level needs evaluation. Medical data, for example, has vastly different privacy requirements than public social media posts. The analysis must also consider the possibility of model inversion attacks where an adversary tries to recover the original dataset based on the distilled dataset and the trained model. Finally, a quantitative assessment of the privacy protection is desirable; bounds on privacy loss or the probability of successful attacks should be provided when possible.

More visual insights

#

More on figures

This figure shows three rows of images for MNIST and CIFAR-100 datasets. The first row contains initialized data, which are real images from the datasets. The second row shows the distilled data generated from real images using techniques described in Section 4.2 of the paper. The third row shows distilled data generated using random noise, based on methods presented in Section 4.1. This comparison demonstrates the differences in data generation techniques and their effect on data realism.

This figure shows the comparison of three different types of data used in the experiment of dataset distillation for Linear Ridge Regression (LRR) with m = 500 data points. The first row is the initialized data used for generating other data; the second row is the distilled data generated from real images using the technique proposed in Section 4.2; and the third row is the distilled data generated from random noise using the technique proposed in Section 4.1. This figure shows the results for MNIST and CIFAR-100 datasets. IPC means Images Per Class.

More on tables

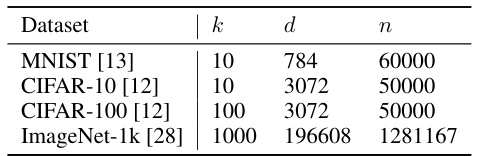
This table presents the number of classes (k), the dimensionality of the data (d), and the number of training samples (n) for four benchmark datasets commonly used in machine learning: MNIST, CIFAR-10, CIFAR-100, and ImageNet-1k. These values provide context for the scale of the datasets used in the experiments and the analysis presented in the paper.

This table presents the results of an experiment designed to validate the theoretical findings of the paper. The experiment compares the performance of original models (trained on the full dataset) against models trained on distilled datasets created using the proposed algorithm. The table shows test accuracy for three different model types (Linear, FCNN, RFF) on three different datasets (MNIST, CIFAR-10, CIFAR-100). The ‘IPC’ column represents the number of images per class in the distilled dataset. The results demonstrate that the analytically-computed distilled datasets effectively recover the original models’ performance.

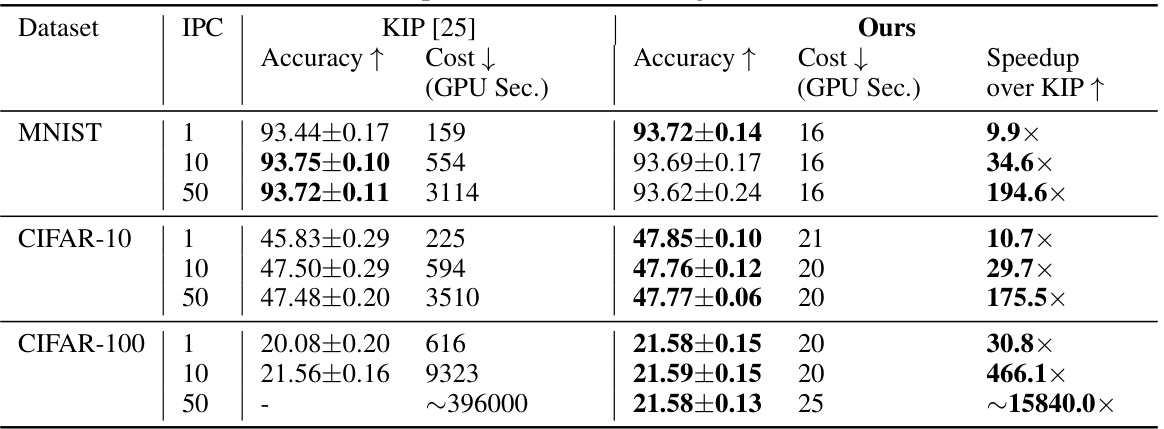
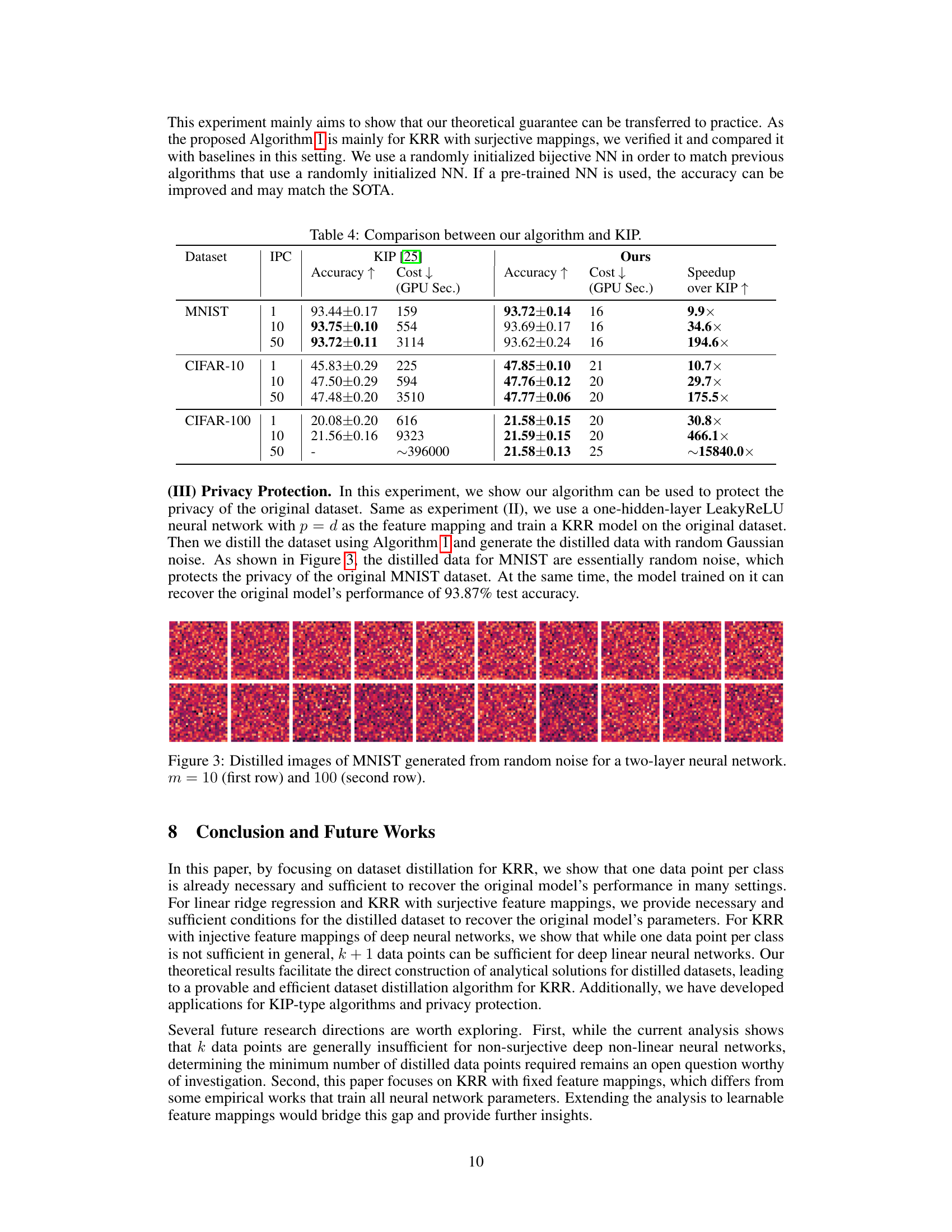
This table compares the performance and computational cost (in GPU seconds) of the proposed dataset distillation algorithm and KIP [25] across various datasets (MNIST, CIFAR-10, and CIFAR-100) and different numbers of distilled images per class (IPC). The results demonstrate that the proposed algorithm achieves comparable accuracy while being significantly faster than KIP.

Full paper

#