Bandits with Preference Feedback: A Stackelberg Game Perspective

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on bandit optimization, particularly in settings with preference feedback and continuous action spaces. It provides a novel algorithm with theoretical guarantees, addressing limitations of existing approaches. This opens avenues for improving the sample-efficiency of algorithms in fields such as human-in-the-loop machine learning and online advertising. The preference-based confidence sequences, are of independent interest for other problems, such as Reinforcement Learning with Human Feedback.

Visual Insights

#

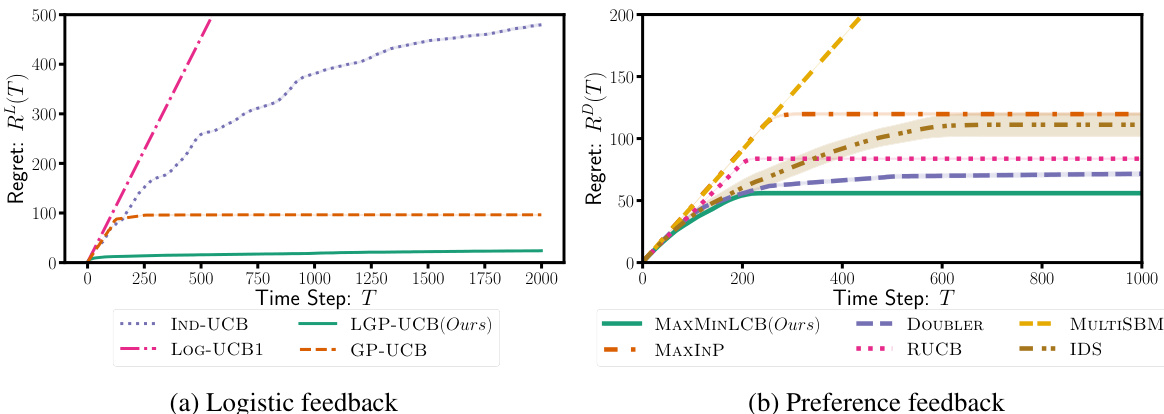
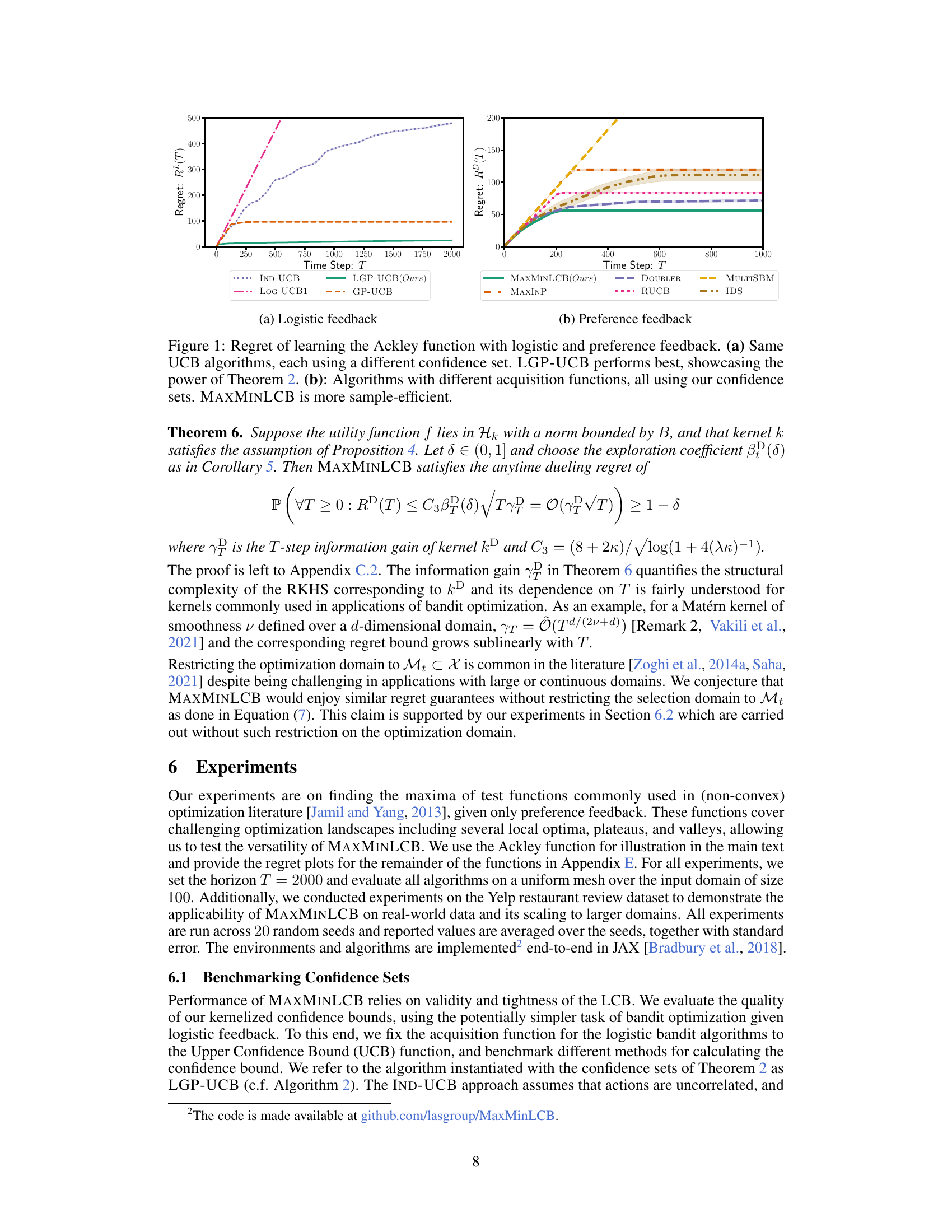
This figure compares the performance of various algorithms on the Ackley function using both logistic and preference feedback. Panel (a) focuses on UCB algorithms, highlighting the superior performance of LGP-UCB (the authors’ algorithm) due to its use of a more effective confidence set (as proven in Theorem 2). Panel (b) compares algorithms with different acquisition functions but the same confidence sets, demonstrating that MAXMINLCB (the authors’ algorithm) is more sample-efficient.

This table presents the results of benchmarking the cumulative dueling regret (RD) for several algorithms across various test utility functions. The experiment was conducted with a time horizon (T) of 2000. The functions are categorized into two groups: smoother functions without steep gradients or local optima (top three rows) and more challenging functions (bottom five rows). The table shows the mean cumulative regret and standard deviation for each algorithm across the different functions, allowing for a comparison of their performance in different optimization landscapes.

In-depth insights

#

Game-Theoretic Bandits

#

Game-theoretic bandits represent a fascinating intersection of game theory and reinforcement learning, offering a powerful framework for sequential decision-making in competitive or uncertain environments. The core idea is to model the interaction between the learning agent and its environment (or other agents) as a game, where the agent’s actions influence not only its own rewards but also the subsequent actions and rewards of other players. This strategic perspective allows for more sophisticated exploration-exploitation strategies. Unlike traditional bandits, which assume a passive environment, game-theoretic bandits explicitly consider the dynamic and potentially adversarial nature of the interactions. By incorporating game-theoretic concepts like Nash equilibrium or Stackelberg equilibrium, algorithms can reason about the optimal strategies of all players involved, leading to improved performance in settings where the environment or other agents actively adapt to the agent’s behavior. A key challenge lies in the computational complexity of finding optimal strategies, especially in large or complex games. However, approximate solutions and efficient algorithms are being actively developed to make game-theoretic bandits applicable in real-world scenarios. Applications range from online advertising and resource allocation to cybersecurity and robotics, where strategic interactions are prevalent.

Confidence Sequences

#

The concept of ‘confidence sequences’ is crucial for quantifying uncertainty in online learning scenarios, especially when dealing with limited or indirect feedback, as explored in the research paper. Traditional confidence intervals provide a snapshot of uncertainty at a single point in time, whereas confidence sequences offer a more dynamic perspective, providing simultaneous confidence bounds across a range of time steps or data points. This is particularly valuable when evaluating the performance of algorithms over time, as in the case of bandits with preference feedback. The construction of these sequences requires careful consideration of the underlying model assumptions and statistical properties, which is often challenging with non-linear or non-parametric rewards. The paper’s novelty potentially lies in developing new preference-based confidence sequences designed to handle infinite action spaces and non-linear utility functions, typically found in realistic applications. The use of these ‘anytime-valid’ confidence sequences allows for more efficient exploration-exploitation trade-offs, as the uncertainty is quantified at every step, leading to improved regret bounds compared to traditional methods. Therefore, the paper’s discussion on confidence sequences significantly contributes to the theoretical foundation and the design of more robust online learning algorithms.

MAXMINLCB Algorithm

#

The MAXMINLCB algorithm innovatively tackles the challenge of bandit optimization with preference feedback in continuous domains by framing the action selection as a zero-sum Stackelberg game. This game-theoretic approach cleverly balances exploration and exploitation. The Leader aims to maximize the lower confidence bound (LCB) of the utility function, ensuring robustness against uncertainty. Simultaneously, the Follower, selecting a competing action, promotes exploration by choosing an optimistic contender. This joint action selection strategy ensures that chosen action pairs are both informative and yield favorable rewards. The algorithm’s effectiveness is further enhanced by the introduction of novel preference-based confidence sequences for kernelized logistic estimators, providing anytime-valid and rate-optimal regret guarantees, outperforming existing methods. The use of the LCB as the objective function, alongside the tight confidence sequences, ensures that MAXMINLCB is both efficient and robust in complex, continuous settings.

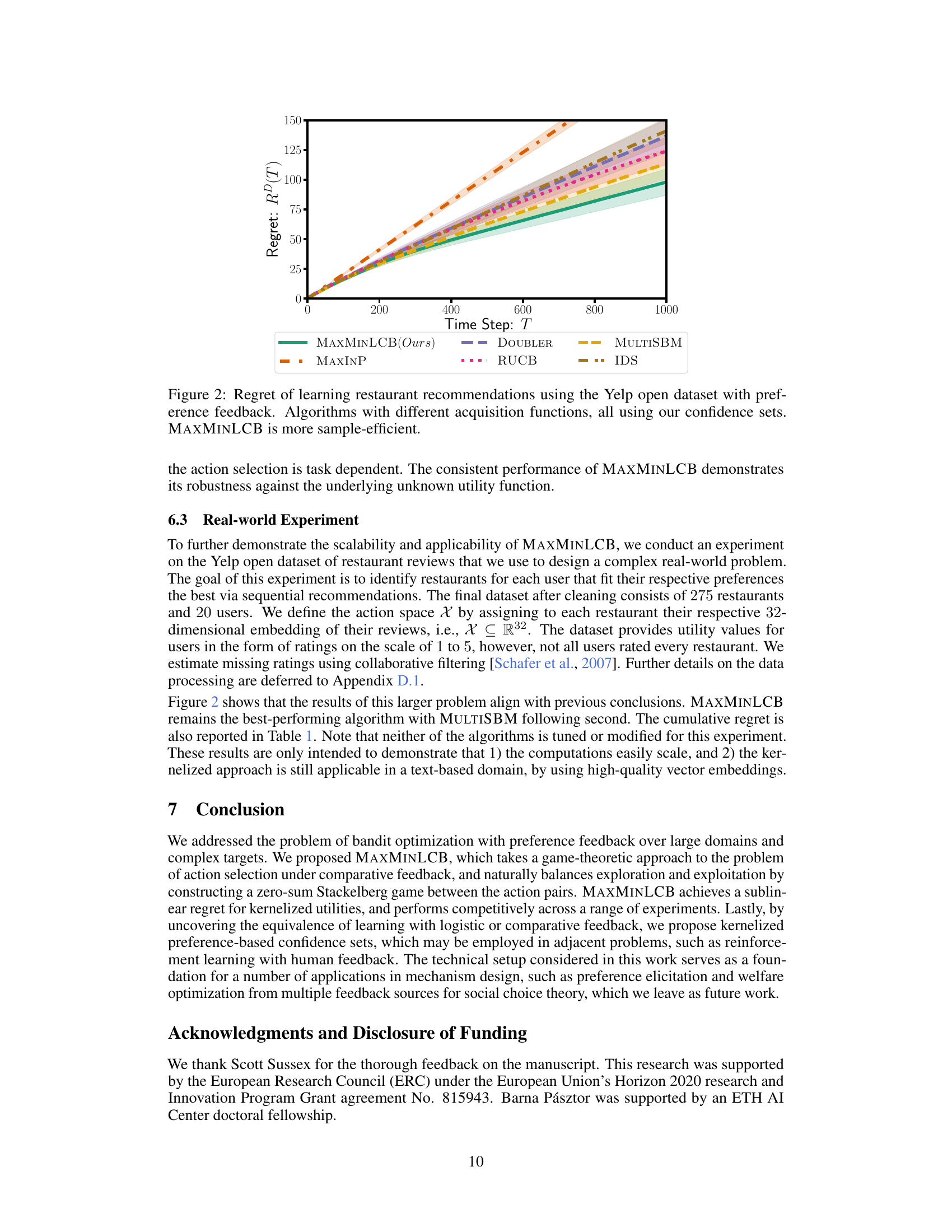
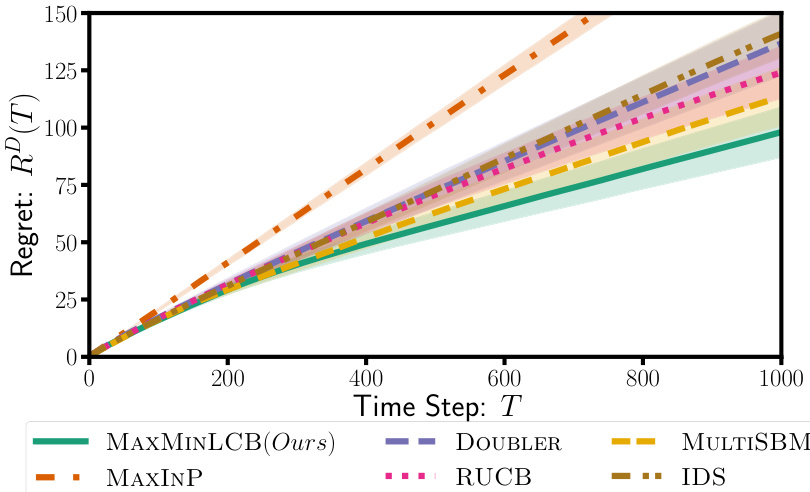
Yelp Experiment

#

The Yelp experiment section is crucial for demonstrating the real-world applicability of the proposed MAXMINLCB algorithm. It moves beyond synthetic benchmark functions to tackle a complex, high-dimensional problem involving restaurant recommendations. Using real user ratings data presents a unique challenge, as this is inherently noisy and contains missing values which needs to be handled carefully. The researchers address this by employing collaborative filtering to estimate missing ratings. The choice to use restaurant embeddings as inputs also highlights the algorithm’s ability to handle non-standard input domains; it directly leverages pre-trained language model embeddings, making the approach readily adaptable to various real-world datasets. The experiment’s success, showing MAXMINLCB outperforming common baselines, underscores its effectiveness in a practical setting. It demonstrates that MAXMINLCB can scale to significant real-world problem sizes, a considerable advantage over existing preference-based bandit algorithms which may not scale efficiently for large datasets. However, the exact specifics of the data preprocessing (e.g., the embedding model used) should be clearly detailed to ensure full reproducibility. While the results show the algorithm’s promise, it’s important to acknowledge that the performance depends on the quality of the input embeddings.

Future Directions

#

Future research could explore several promising avenues. Extending MAXMINLCB to handle more complex feedback mechanisms, such as those incorporating uncertainty or ordinal preferences, would enhance its applicability. Investigating alternative game-theoretic formulations beyond the Stackelberg game framework could lead to more efficient algorithms. Developing tighter regret bounds is crucial, particularly in high-dimensional settings. Addressing the computational cost of MAXMINLCB, especially for high-dimensional spaces, is another important area. This could involve exploring more efficient optimization strategies or using approximations. Finally, empirical evaluation on a wider variety of real-world problems is needed to demonstrate its robustness and general applicability, potentially with a focus on areas like human-in-the-loop machine learning and active learning.

More visual insights

#

More on figures

This figure compares the performance of different algorithms in learning the Ackley function under two feedback settings: logistic feedback and preference feedback. Panel (a) shows that for logistic feedback, the algorithm using the novel confidence sets (LGP-UCB) outperforms others that use different confidence sets. Panel (b) focuses on preference feedback, demonstrating that MAXMINLCB, which uses the novel confidence sets, significantly outperforms existing algorithms in terms of sample efficiency (lower regret).

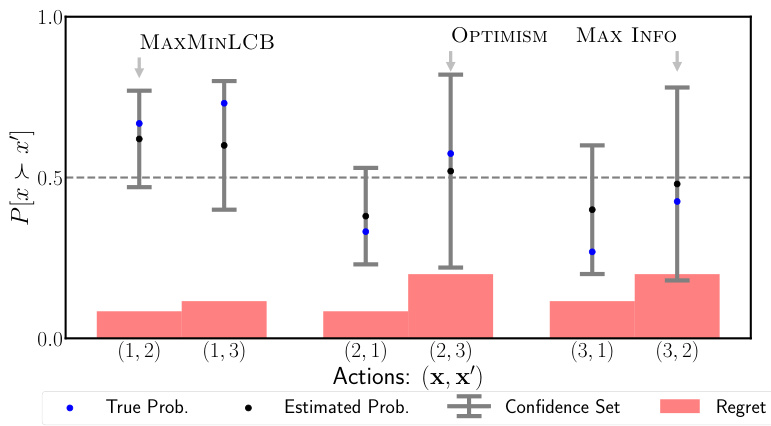
This figure compares three different action selection strategies: MAXMINLCB, OPTIMISM, and MAX INFO. For a simple problem with three arms, it shows the true probability of one arm being preferred over another (blue dots), the estimated probability with confidence intervals (black dots and error bars), and the resulting regret of each action pair (red bars). MAXMINLCB selects the action pair with the lowest regret, demonstrating its ability to balance exploration and exploitation effectively. In contrast, OPTIMISM and MAX INFO methods select sub-optimal actions, showcasing MAXMINLCB’s superiority.

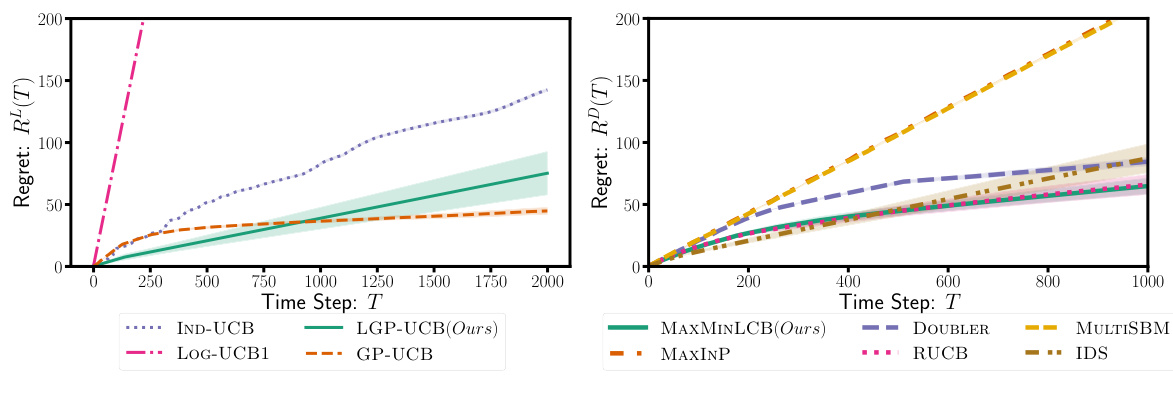
This figure shows the results of two experiments using the Ackley function. The left plot compares several UCB algorithms using different confidence sets for the logistic feedback setting. The right plot compares several algorithms with different acquisition functions, all using the same confidence sets, for the preference feedback setting. The results demonstrate that LGP-UCB (using the proposed confidence set) is more sample-efficient in the logistic feedback setting, and MAXMINLCB is more sample-efficient in the preference feedback setting.

This figure compares the performance of several algorithms on the Ackley function using both logistic and preference feedback. Panel (a) shows that for logistic feedback, LGP-UCB, which uses a novel confidence set derived in Theorem 2, outperforms other UCB algorithms. Panel (b) shows that for preference feedback, MAXMINLCB, using the authors’ confidence sets, is more sample-efficient than other algorithms.

Full paper

#