Implicit Bias of Mirror Flow on Separable Data

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers studying implicit bias in machine learning. It provides a formal characterization of the implicit bias of mirror descent, a widely used optimization algorithm, for linearly separable classification problems. This bridges a gap in the current understanding and opens avenues for research into more complex scenarios.

Visual Insights

#

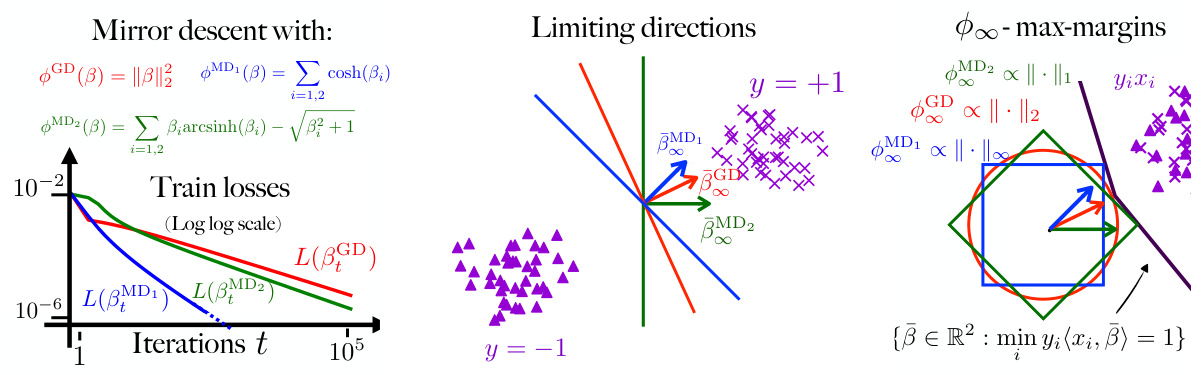
This figure shows a comparison of three different mirror descent algorithms on a linearly separable 2D dataset. The left panel shows the training loss curves for gradient descent (GD) and two mirror descent methods (MD1 and MD2) with different potentials. The center panel illustrates the directional convergence of the iterates toward different separating hyperplanes, highlighting how the choice of potential influences the algorithm’s behavior. The right panel visualizes the maximum margin solutions corresponding to each potential, illustrating that the limiting direction is proportional to the argument that minimizes the horizon function of the potential under a margin constraint, as stated by Theorem 1. The full trajectories are shown in Figure 4, and more detail is provided in Section 5.

In-depth insights

#

Mirror Flow Bias

#

The concept of “Mirror Flow Bias” refers to the implicit biases exhibited by mirror descent algorithms, specifically mirror flow, in linearly separable classification problems. Mirror flow, a continuous-time analog of mirror descent, doesn’t converge to a single solution but rather exhibits directional convergence towards a specific solution within the set of optimal solutions. This direction is determined by the algorithm’s mirror potential, a function that shapes the algorithm’s geometry. The bias is not random; it’s a systematic preference determined by the choice of potential. The paper finds that for exponential-tailed losses and under suitable assumptions, this direction is often towards a maximum margin classifier, although the specific norm defining the margin depends on the potential. This highlights that the training algorithm significantly impacts the final model, especially in cases with many optimal solutions. Understanding mirror flow bias is crucial for interpreting the behavior of neural networks and gradient-based optimization, as mirror descent structure frequently arises within these algorithms. The research reveals a simple formula to assess the bias when the potential is separable, offering valuable insights into how the training process implicitly regularizes the final model’s properties.

Separable Data

#

The concept of “separable data” is central to the study of implicit bias in machine learning, particularly within the context of classification problems. When data is separable, it means there exists a hyperplane (or more generally, a decision boundary) that perfectly separates the data points into their respective classes. This seemingly simple condition has profound implications. Linear separability, for instance, allows for straightforward classification using linear models, but it also significantly reduces the complexity of the optimization problem, potentially leading to an abundance of solutions that perfectly fit the training data. The paper explores how different training algorithms, specifically focusing on mirror descent and its continuous-time counterpart (mirror flow), select a specific solution from this vast set of perfect classifiers. The focus on separable data provides a controlled setting to dissect the implicit regularization properties of these methods. The algorithm’s behavior, therefore, is not solely determined by the loss function being minimized (which is identically zero for all perfect classifiers) but rather by the properties of the mirror potential that guides the optimization process. This analysis is crucial because it sheds light on the ways in which these optimization algorithms, beyond simply minimizing the training loss, intrinsically incorporate certain structural biases, ultimately influencing their generalization capabilities to unseen data.

Horizon Function

#

The concept of a ‘Horizon Function’ in the context of the provided research paper is crucial for understanding the asymptotic behavior of mirror descent. It characterizes the shape of the potential function at infinity, capturing how the algorithm’s iterates behave as they diverge. The horizon function, denoted as φ∞, is not directly derived from the original potential function φ but rather constructed using the limiting behavior of the normalized sub-level sets of φ. This construction elegantly handles the complexity of non-homogeneous potentials, providing a powerful tool for analyzing the implicit bias of mirror descent, which otherwise remains elusive. The paper demonstrates the significance of φ∞ by showing that the asymptotic direction of mirror flow converges to the solution that minimizes φ∞ under a max-margin constraint. The ability to compute φ∞, especially for separable potentials, offers practical applicability, allowing the analysis of a large class of mirror descent algorithms. Therefore, the horizon function significantly advances our understanding of implicit regularization in machine learning by providing a unifying framework to analyze the limiting behavior of mirror descent for diverse potentials.

Max-Margin

#

The concept of “max-margin” is central to many classification algorithms. It refers to the idea of finding a decision boundary (e.g., a hyperplane) that maximizes the distance between the boundary and the nearest data points of different classes. This approach is motivated by the intuition that a larger margin implies better generalization performance. The paper explores this concept in the context of mirror descent, a family of optimization algorithms which generalize gradient descent. It investigates how different mirror potentials (which specify the geometry of the optimization) affect which of the many possible maximum-margin solutions is selected by the algorithm, revealing an implicit bias that can lead to different generalization properties. This work offers a comprehensive mathematical framework for understanding this selection process, providing insights into how the algorithm’s behavior is linked to the shape of the potential. Furthermore, it introduces the notion of a “horizon function”, characterizing the potential’s behavior at infinity and enabling a simple formula for computing this function in separable cases. This offers a new tool for analyzing and understanding the implicit bias in various machine-learning algorithms, especially those whose underlying structure closely resembles mirror descent.

Future Research

#

The authors propose several avenues for future research, acknowledging the limitations of their asymptotic analysis. A primary focus is determining the convergence rate of the normalized iterates towards the maximum-margin solution. This is crucial for understanding the practical implications of the theoretical results. Further investigation is needed to extend the analysis to potentials with non-coercive gradients, particularly relevant in deep learning architectures. The analysis does not cover potentials defined only on strict subsets of R^d, which also requires attention. Finally, exploring the impact of different loss functions beyond the exponential tails, broadening the scope to incorporate polynomial tails, would offer deeper insights into the algorithm’s behavior.

More visual insights

#

More on figures

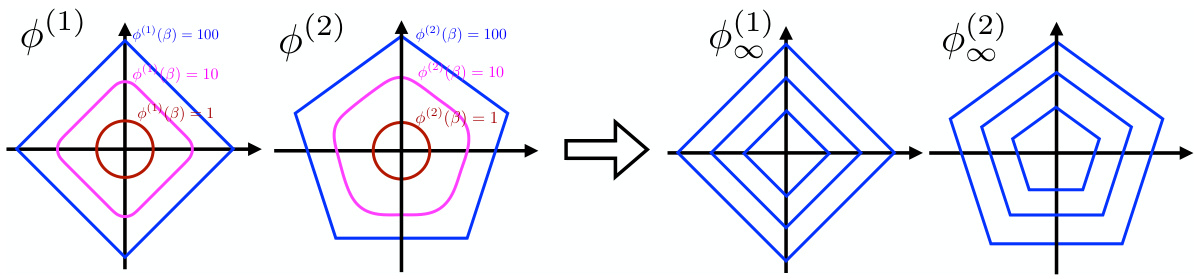
This figure illustrates the concept of horizon functions. The left two subfigures show level lines of two different potential functions, φ(1) and φ(2). The right two subfigures display the corresponding horizon functions, φ(1)∞ and φ(2)∞, which capture the asymptotic shape of the potential functions ‘at infinity’. The horizon functions are crucial for characterizing the implicit bias of mirror descent.

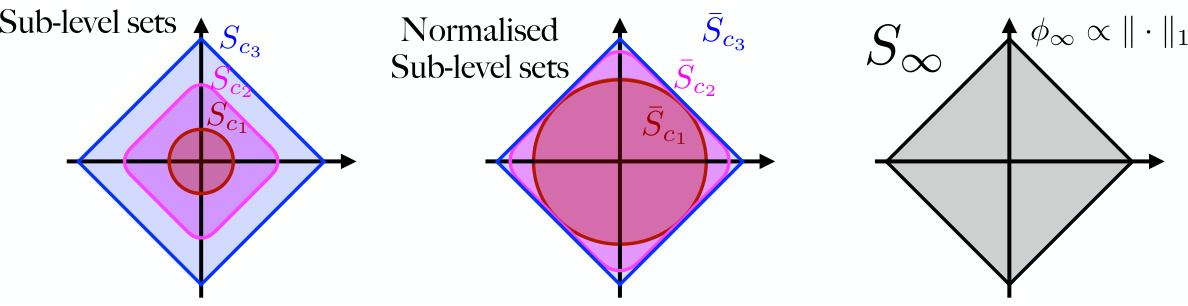
This figure illustrates the construction of the horizon shape S∞, which is crucial for understanding the implicit bias of mirror flow in the classification setting. The left panel shows how the sub-level sets Sc of a potential function change shape and increase as c grows. To prevent the sub-level sets from blowing up, the middle panel shows the normalized sub-level sets Šc, which are constrained to the unit ball using the l1-norm. Finally, the right panel shows that as c approaches infinity, the normalized sub-level sets converge to a limiting set S∞, using the Hausdorff distance, which defines the horizon function φ∞.

This figure shows the trajectories of mirror flow for three different potentials (GD, MD1, MD2) on a 2D linearly separable dataset. The left panel illustrates the iterates diverging to infinity, demonstrating that the algorithm’s behavior depends on the potential used. The right panel presents the rescaled trajectories, where the iterates are normalized. They converge to their respective ∞-maximum-margin predictors, confirming the theoretical findings of Theorem 2, which formally characterizes the implicit bias of mirror flow for separable classification problems.

Full paper

#