↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep ensembles, combining multiple neural networks, have shown promise in improving model robustness and accuracy. However, recent studies highlight that the sharpness of individual models’ loss landscapes and the diversity among these models are key factors influencing the ensemble’s performance. This paper investigates the complex relationship between sharpness and diversity, revealing a trade-off: minimizing sharpness tends to reduce diversity, limiting the potential gains from ensembling. This poses a significant challenge for optimizing ensemble performance.
To address this challenge, the authors propose SharpBalance, a novel training approach. SharpBalance strategically balances sharpness and diversity by training each individual model on a carefully selected subset of the training data focusing on reducing sharpness while maintaining overall diversity. Theoretical analysis and empirical evaluations on various datasets demonstrate that SharpBalance effectively improves ensemble performance in both in-distribution and out-of-distribution scenarios, outperforming baseline methods by a significant margin. This work significantly advances the understanding and optimization of deep ensembles.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses a critical gap in understanding the interplay between sharpness and diversity in deep ensembles. The findings challenge existing practices and open new avenues for improving ensemble performance, particularly in handling out-of-distribution data, a major concern in machine learning. This research will significantly influence future ensemble learning strategies and methodologies.
Visual Insights#

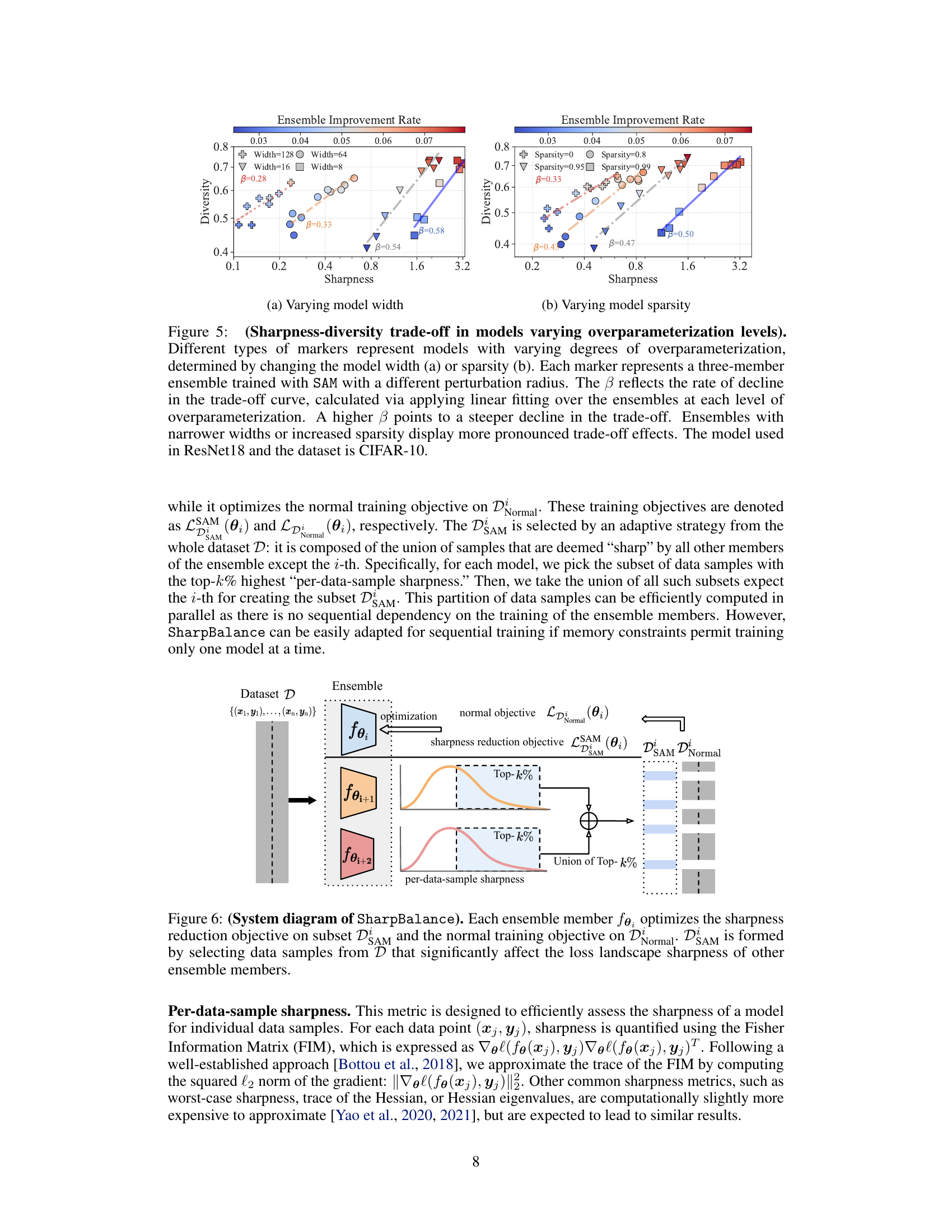
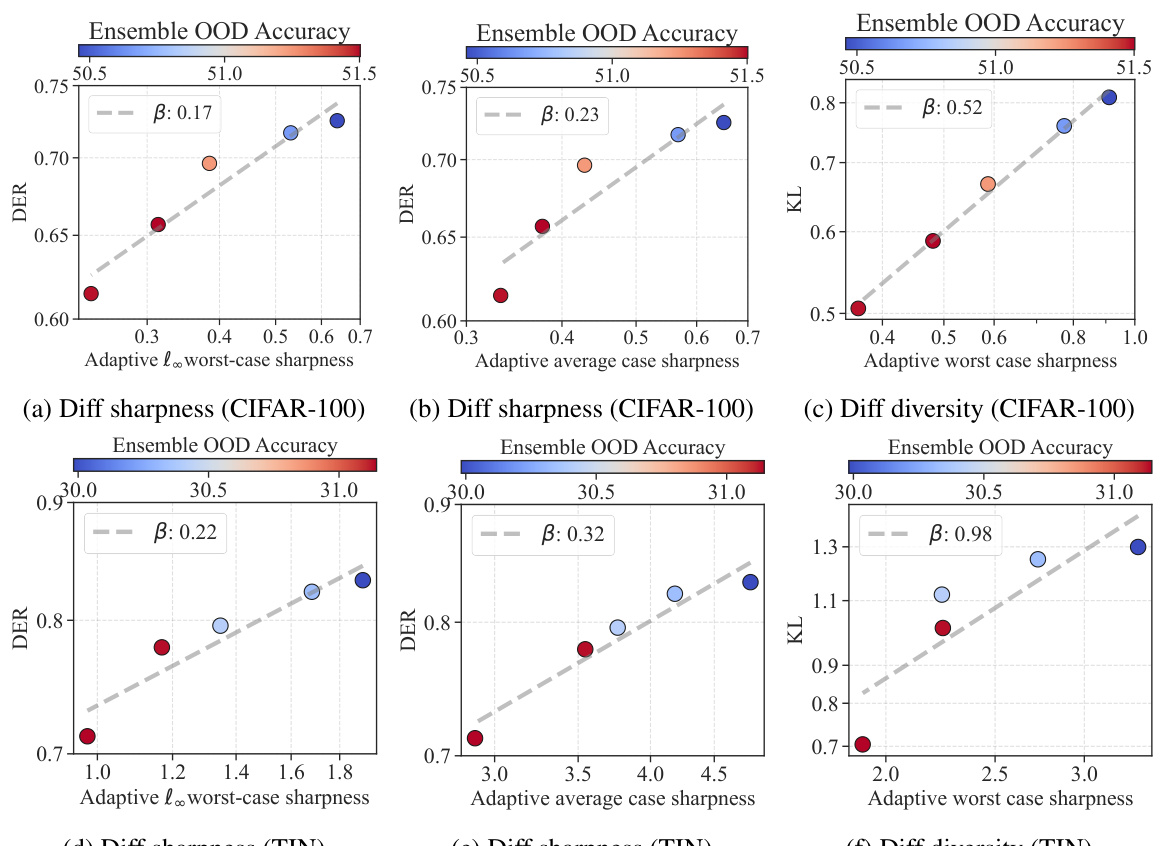
This figure illustrates the sharpness-diversity trade-off and how SharpBalance addresses it. (a) shows a caricature of the trade-off, where minimizing sharpness reduces diversity. (b) presents theoretical results showing SharpBalance improves the trade-off. (c) shows empirical results on CIFAR-10 confirming the improvement.
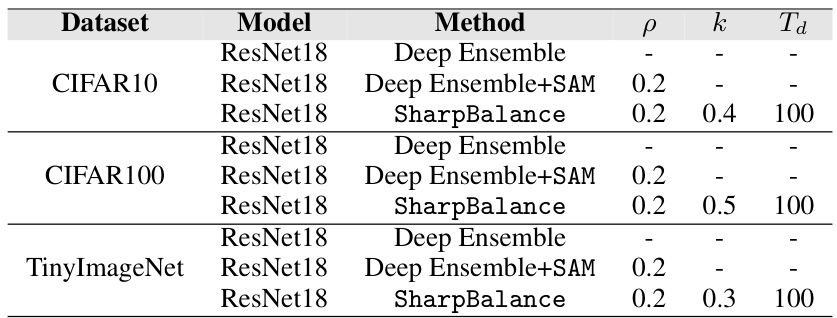
This table shows the hyperparameter settings used for the experiments presented in Section 4.4 of the paper. It lists the optimal values for the perturbation radius (p) and the top-k percentage of data samples used for the SharpBalance method (k). The table also specifies the Td parameter, and indicates that each result shown in Figure 7 is an average across three ensembles and nine different random seeds.
In-depth insights#
Sharp-Diversity Tradeoff#
The Sharpness-Diversity Tradeoff section in this research paper explores a crucial relationship between the sharpness of loss landscape minima and the diversity of models within deep ensembles. The core finding is that reducing sharpness, while often improving individual model generalization, can paradoxically reduce ensemble diversity, ultimately hindering overall ensemble performance. This trade-off is rigorously examined, with theoretical analysis and experiments showing that minimizing sharpness through techniques like Sharpness-Aware Minimization (SAM) can negatively impact diversity. The paper further introduces SharpBalance, a novel training approach designed to mitigate this trade-off by balancing sharpness reduction with diversity maintenance. SharpBalance achieves this by training each ensemble member on a carefully selected subset of the data, aiming to optimize sharpness while avoiding diversity reduction. Empirical results across various datasets demonstrate the effectiveness of this strategy and show a significant improvement in both in-distribution (ID) and out-of-distribution (OOD) scenarios.
SharpBalance Method#
The SharpBalance method is a novel training approach designed to address the sharpness-diversity trade-off in deep ensembles. It achieves this by training each ensemble member on a different subset of the data, aiming to reduce sharpness without sacrificing the beneficial diversity of the ensemble. This strategy is theoretically grounded, showing that a better sharpness-diversity balance is attainable through the proposed approach. Empirical evaluations demonstrate significant improvements in both in-distribution and out-of-distribution settings, surpassing baseline methods across various datasets. The core innovation lies in its data-dependent approach to sharpness-aware minimization, adaptively balancing model sharpness and the diversity among models within the ensemble, resulting in robust generalization and improved performance.
Empirical Validation#
An empirical validation section in a research paper would rigorously test the study’s hypotheses. It would involve designing experiments to measure key variables and using statistical methods to determine whether observed results support or refute the hypotheses. The methods employed should be clearly stated, including the datasets, metrics, and experimental setup. A strong validation would consider potential confounding factors and include controls to mitigate their influence, ensuring the validity and reliability of the results. Visualizations, such as graphs or tables, are usually included to present the findings concisely and effectively. It is critical that the validation section demonstrates reproducibility; sufficient detail must be included to enable other researchers to replicate the study and obtain similar findings. A discussion of limitations and potential biases is also crucial to fully assess the significance and generalizability of the results. Finally, the validation section’s findings should be carefully related back to the original hypotheses and the broader research questions, drawing meaningful conclusions and implications.
Theoretical Analysis#
The theoretical analysis section of this research paper is crucial as it provides a formal justification for the observed sharpness-diversity trade-off in deep ensembles. The authors employ rigorous mathematical analysis to show that minimizing sharpness, while seemingly beneficial, can lead to a reduction in ensemble diversity, potentially hindering performance. Key theorems are presented, establishing the existence of this trade-off and quantifying the relationship between sharpness and diversity under specific conditions. The use of random matrix theory is noteworthy, enabling analysis of model behavior under realistic assumptions about data distribution. This theoretical foundation strengthens the paper’s contribution by proving not just empirical observations but also the underlying mathematical principles at play. The analysis of SharpBalance within this framework then demonstrates its efficacy in achieving a better trade-off, improving both sharpness and diversity, highlighting the mathematical superiority of the proposed method. The clear presentation of theorems and proofs ensures the reproducibility and verifiability of the key findings. Overall, the theoretical analysis transforms empirical results into provable statements about the core mechanisms governing the success of deep ensemble methods.
Limitations & Future#
The research on sharpness-diversity trade-offs in deep ensembles presents valuable findings but also reveals limitations. Theoretically, the analysis relies on assumptions like Gaussian data distributions and quadratic objectives, which may not always hold in real-world scenarios. Empirically, while SharpBalance shows improvements, the extent of generalization across diverse datasets and architectures remains to be fully explored. Future work could address these limitations by: 1) relaxing the theoretical assumptions to encompass more realistic data characteristics and loss functions; 2) conducting more extensive experiments across a broader range of datasets, model architectures, and ensemble sizes to better assess the robustness and generalizability of SharpBalance; 3) investigating alternative approaches to balance sharpness and diversity, perhaps incorporating adaptive methods that dynamically adjust the balance during training; and 4) exploring the impact of different optimization strategies and hyperparameter settings on the trade-off. Addressing these limitations will enhance the reliability and applicability of SharpBalance in practical settings.
More visual insights#
More on figures
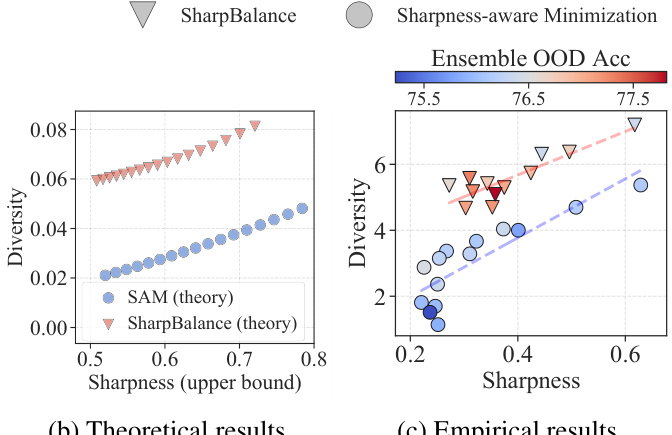
This figure illustrates the sharpness-diversity trade-off and how SharpBalance addresses it. Subfigure (a) uses a visual metaphor to show how reducing sharpness (making the loss landscape smoother) can reduce diversity in an ensemble. Subfigure (b) presents theoretical results supporting this trade-off, showing that SharpBalance achieves better diversity for the same sharpness. Subfigure (c) validates these findings with empirical results from CIFAR-10.
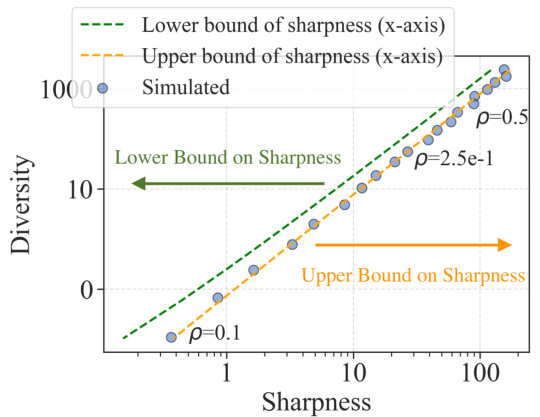
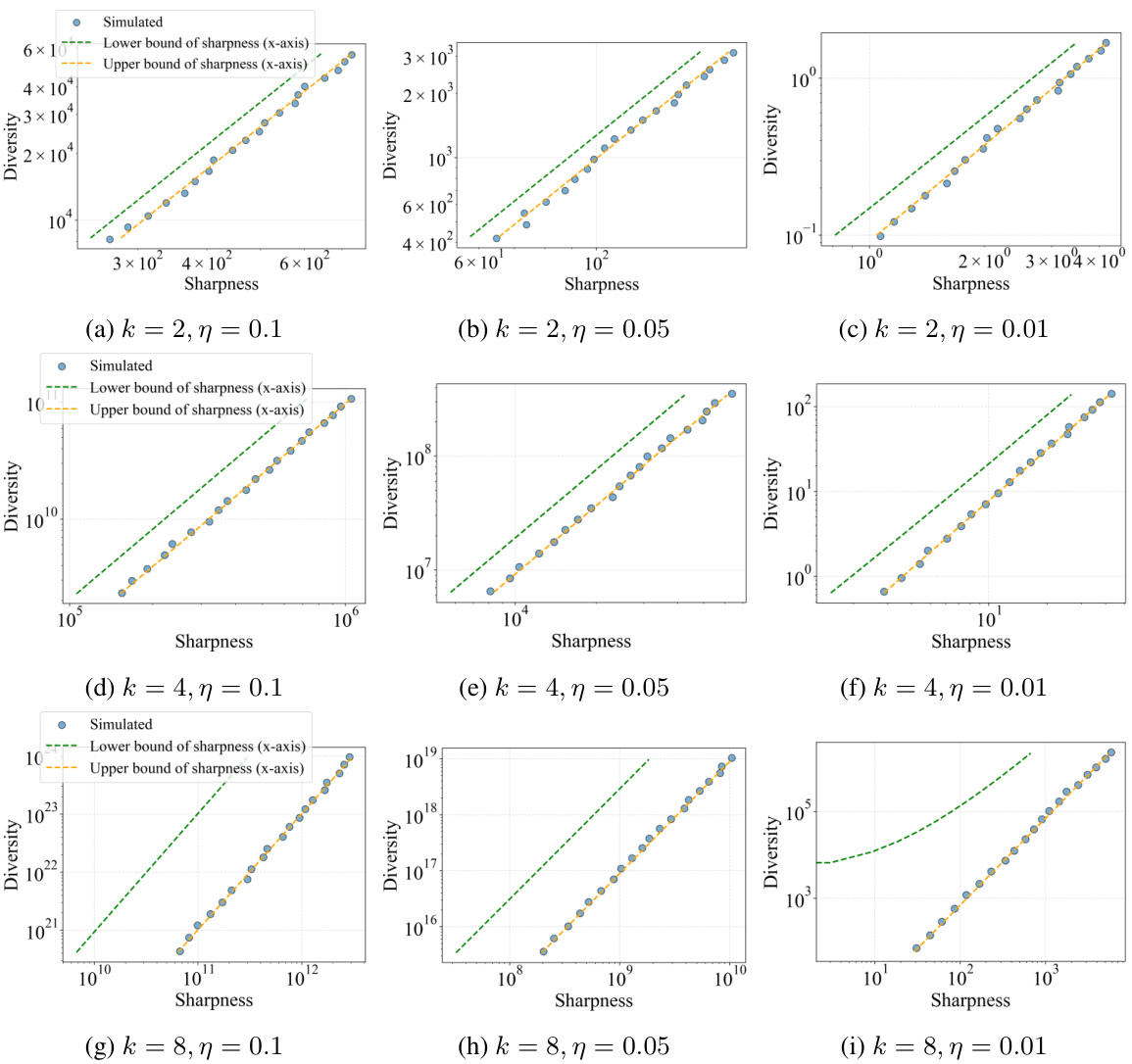
This figure empirically validates Theorem 1, which theoretically analyzes the sharpness-diversity trade-off. It plots the simulated sharpness and diversity against each other. Each point represents a model trained using SAM (Sharpness-Aware Minimization) with a different perturbation radius (p). The plot shows that increasing sharpness reduces diversity, supporting the existence of this trade-off. The theoretical upper and lower bounds for sharpness derived in Theorem 1 are also plotted for comparison, showing a good match with empirical results.
This figure illustrates the sharpness-diversity trade-off and how SharpBalance addresses it. Panel (a) shows a cartoon illustrating the trade-off: reducing sharpness improves individual model performance but reduces diversity, hindering ensemble performance. SharpBalance aims to improve this. Panel (b) shows theoretical results supporting the existence of this trade-off, and how SharpBalance improves it. Panel (c) shows empirical results confirming these findings, showing improved ensemble performance with SharpBalance.
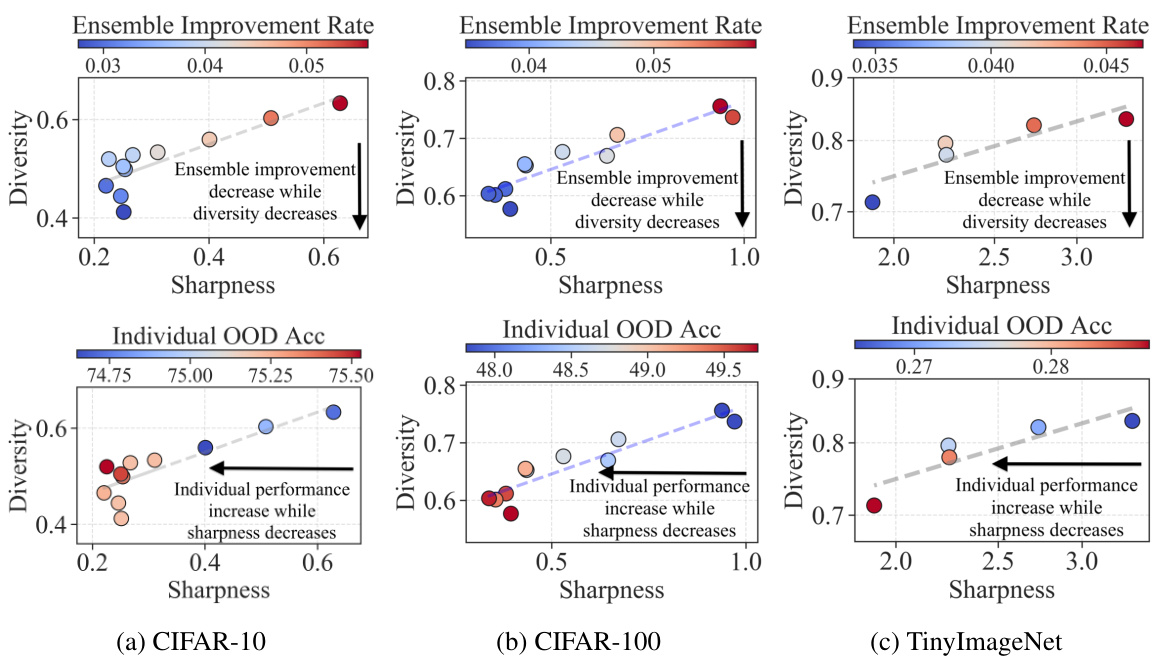
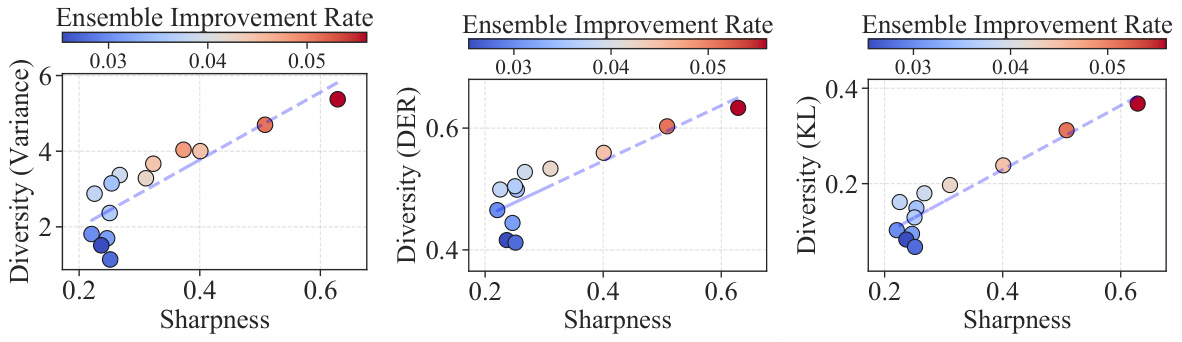
This figure empirically validates the sharpness-diversity tradeoff. It shows that while reducing sharpness improves individual model performance, it negatively affects ensemble performance by reducing diversity. This trade-off is demonstrated across three datasets (CIFAR-10, CIFAR-100, and TinyImageNet) using different metrics for measuring both sharpness and diversity.

This figure empirically validates the sharpness-diversity trade-off phenomenon. It shows that while decreasing the sharpness of individual models (x-axis) improves their individual performance (bottom row), it also decreases the diversity among the models (y-axis). This diversity reduction negatively impacts the overall ensemble improvement rate (top row), illustrating the trade-off between sharpness and diversity.

This figure empirically validates the sharpness-diversity trade-off across different model architectures (varying width and sparsity). It shows that reducing sharpness improves individual model performance, but simultaneously reduces diversity, leading to less ensemble improvement. The trade-off is more pronounced in smaller or sparser models, illustrated by steeper curves.
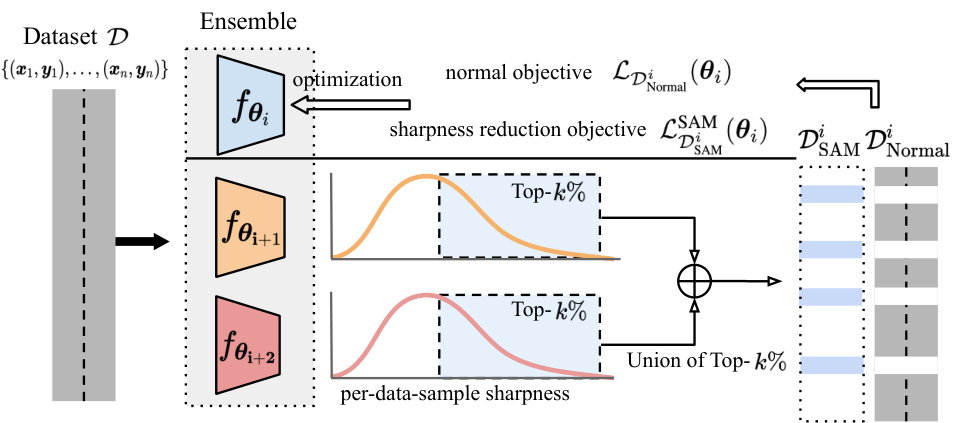
This figure illustrates the SharpBalance algorithm. It divides the training dataset into two subsets for each ensemble member: a ‘sharpness-aware set’ and a ’normal set’. The sharpness-aware set is constructed by identifying data points that significantly influence the sharpness of other ensemble members. The model is then trained to minimize sharpness on the sharpness-aware set and the standard training objective on the normal set. This process aims to balance sharpness and diversity in the ensemble.
This figure illustrates the sharpness-diversity trade-off and how SharpBalance addresses it. Panel (a) shows a cartoon illustrating how minimizing sharpness (smoothness of the loss landscape) reduces diversity in an ensemble of neural networks. Panel (b) presents theoretical results supporting the existence of this trade-off and demonstrating that SharpBalance improves upon it. Panel (c) provides empirical validation of these findings on the CIFAR-10 dataset.

This figure empirically validates the sharpness-diversity trade-off phenomenon. It shows that while reducing sharpness improves individual model performance (OOD accuracy), it reduces ensemble diversity, which negatively impacts the ensemble improvement rate (EIR). The results are shown across three datasets (CIFAR-10, CIFAR-100, TinyImageNet), each with different sharpness and diversity levels obtained by varying the perturbation radius (p) in SAM.
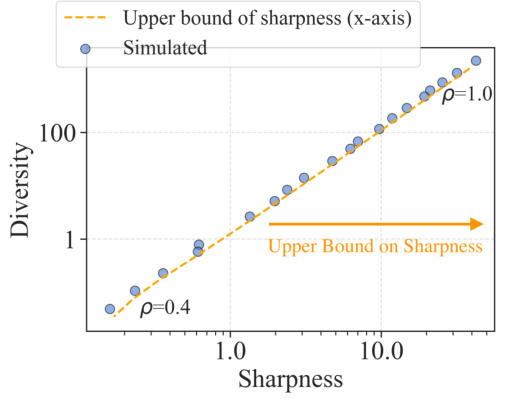
This figure empirically validates Theorem 1 by comparing theoretical and simulated sharpness-diversity trade-off curves. Each point represents a model trained using SAM with different perturbation radius values. The plot shows the relationship between sharpness (x-axis) and diversity (y-axis). The theoretical upper and lower bounds of the sharpness are also plotted. The close alignment between simulated and theoretical results demonstrates the accuracy of Theorem 1.
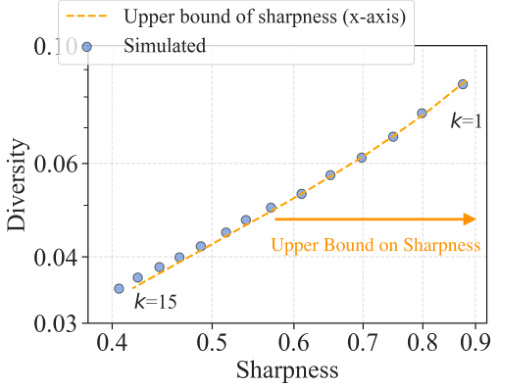
This figure empirically validates the theoretical sharpness-diversity trade-off predictions from Theorem 2 of the paper. Two subfigures are shown: one varies the perturbation radius (p) of the SAM optimizer, and the other varies the number of training iterations (k). The results show that the observed sharpness and diversity closely match the theoretical upper and lower bounds, supporting the theoretical analysis.
This figure illustrates the sharpness-diversity tradeoff and how SharpBalance addresses it. (a) shows a caricature of the tradeoff, where lower sharpness leads to lower diversity, which is undesirable for ensembles. (b) presents theoretical results supporting the existence of this tradeoff and showing that SharpBalance improves it. (c) presents empirical results demonstrating the improved sharpness-diversity tradeoff achieved by SharpBalance.
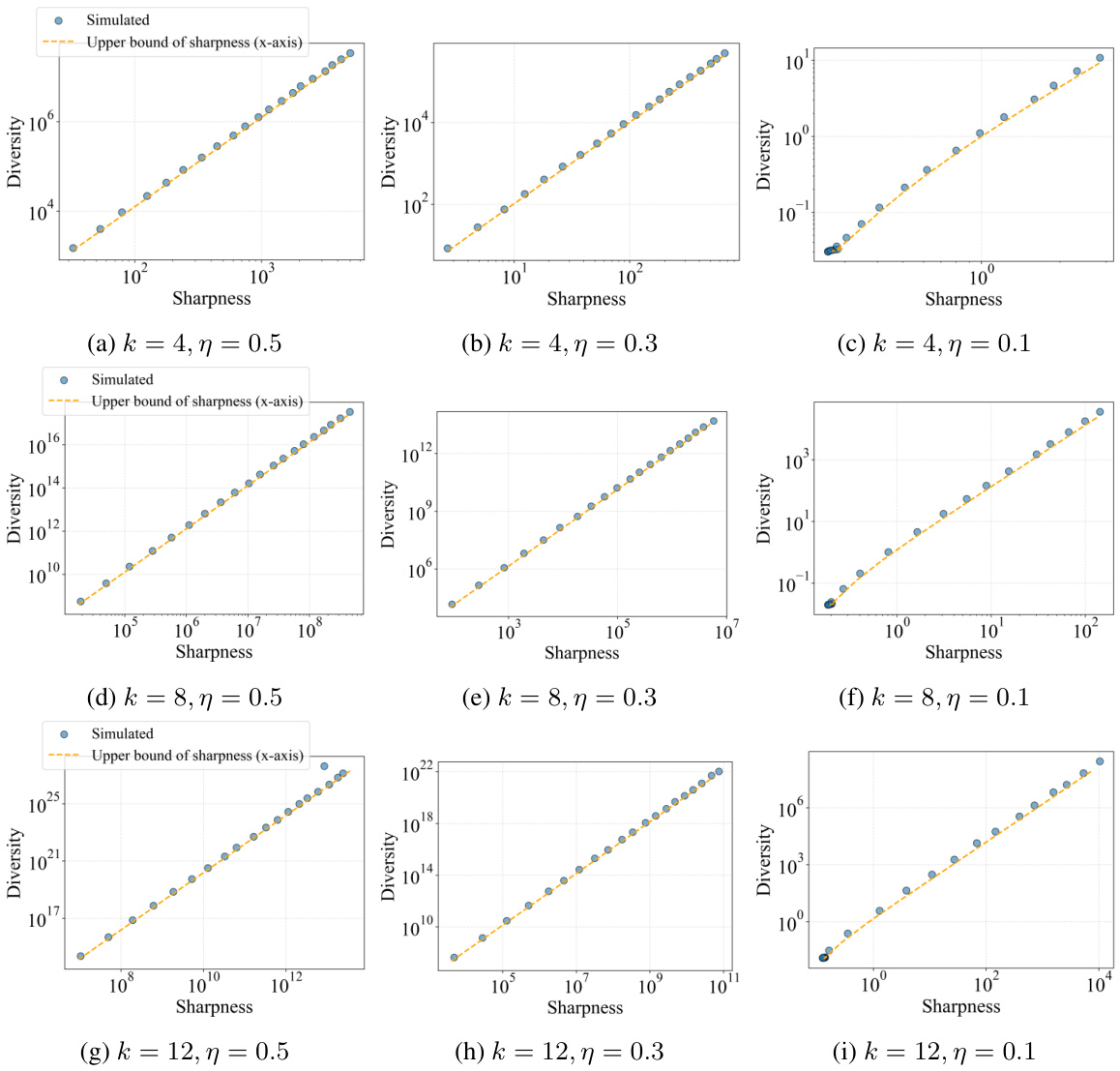
This figure empirically validates the sharpness-diversity trade-off phenomenon. It shows that reducing sharpness improves individual model performance (OOD accuracy) but simultaneously reduces diversity, leading to a decrease in the ensemble improvement rate. This is demonstrated across three datasets (CIFAR-10, CIFAR-100, TinyImageNet), using different sharpness levels achieved by varying the perturbation radius in the SAM optimizer.
This figure empirically validates the sharpness-diversity trade-off. It shows that reducing sharpness improves individual model performance but reduces diversity within the ensemble, ultimately leading to a decrease in ensemble improvement. The results are shown across three datasets (CIFAR-10, CIFAR-100, and TinyImageNet), illustrating the generality of the trade-off.

This figure empirically validates the sharpness-diversity trade-off phenomenon. It shows that lowering sharpness improves individual model performance (OOD accuracy), but simultaneously reduces the diversity within the ensemble, negatively affecting the ensemble improvement rate (EIR). This trade-off is observed across three different datasets (CIFAR-10, CIFAR-100, TinyImageNet).

This figure illustrates the sharpness-diversity trade-off and how SharpBalance addresses it. Panel (a) shows a cartoon illustrating how minimizing sharpness (making the loss landscape smoother) reduces diversity in an ensemble of neural networks. Panel (b) presents theoretical results supporting the existence of this trade-off and demonstrating that SharpBalance improves it. Panel (c) shows empirical results verifying the trade-off and the effectiveness of SharpBalance on CIFAR-10.
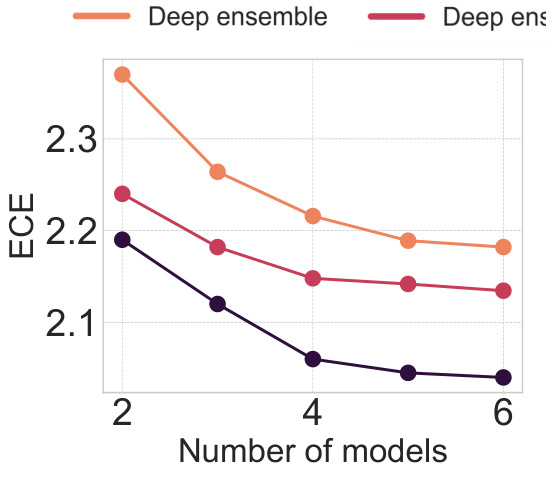
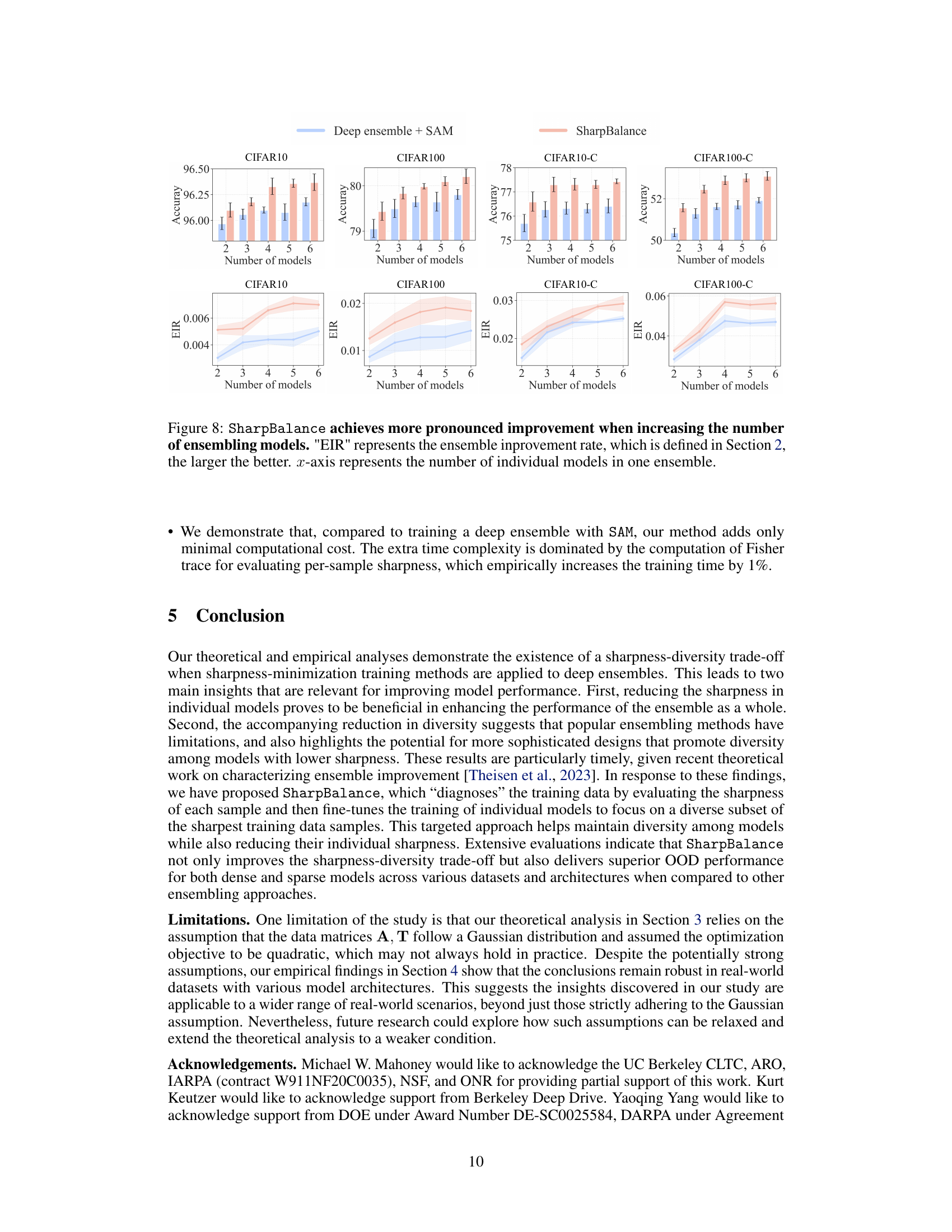
This figure shows the expected calibration error (ECE) and negative log-likelihood (NLL) for different numbers of models in the ensemble. Lower values for both ECE and NLL indicate better uncertainty estimates and improved model performance. The results show that SharpBalance consistently outperforms both a standard deep ensemble and a deep ensemble trained with SAM (Sharpness-Aware Minimization), across all ensemble sizes. This supports the paper’s claim that SharpBalance improves the sharpness-diversity tradeoff and leads to better calibrated uncertainty estimates.

This figure shows the expected calibration error (ECE) and negative log-likelihood (NLL) for different ensemble sizes using three different methods: Deep ensemble, Deep ensemble + SAM, and SharpBalance. Both ECE and NLL are lower is better, indicating better uncertainty estimates. The results show that SharpBalance consistently outperforms the other two methods across different ensemble sizes, indicating that it provides more reliable uncertainty estimates.
More on tables

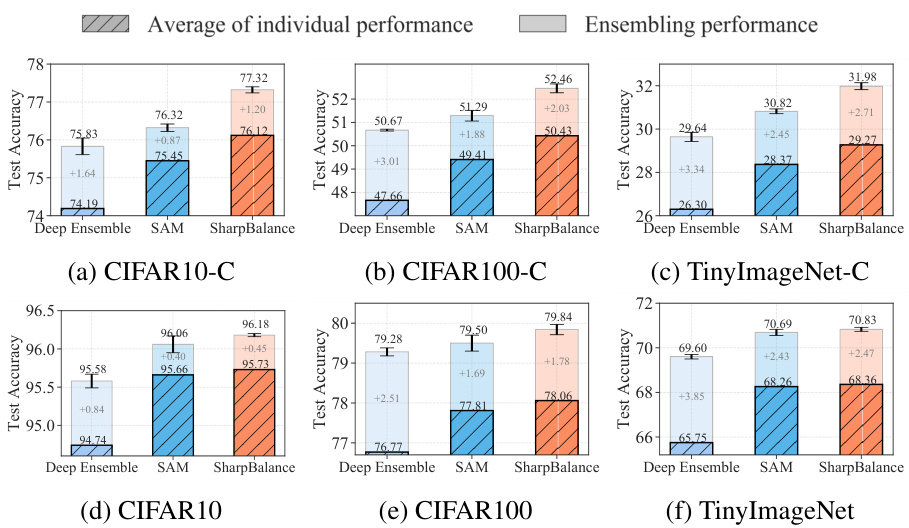
This table shows the performance of three different ensemble methods (Deep ensemble, Deep ensemble+SAM, and SharpBalance) on CIFAR-10C dataset with different corruption severities (1-5). The numbers represent the test accuracy. The values in parentheses show the improvement of SharpBalance over the Deep ensemble+SAM method.

This table presents the results of the CIFAR-100-C dataset with different corruption levels. It compares the performance of three methods: Deep ensemble, Deep ensemble+SAM, and SharpBalance. The numbers represent the accuracy, and the numbers in parentheses indicate the improvement of SharpBalance compared to Deep ensemble+SAM. SharpBalance consistently outperforms the other methods across all corruption levels.

This table presents the results of evaluating the performance of three different ensemble methods (Deep ensemble, Deep ensemble+SAM, and SharpBalance) on the Tiny-ImageNet-C dataset with varying corruption severity levels. The numbers represent the accuracy achieved by each method under different corruption conditions. The numbers in parentheses represent the improvement achieved by SharpBalance compared to the Deep ensemble+SAM method. The data shows that SharpBalance consistently outperforms the other two methods across all corruption levels.

This table shows the results of additional experiments performed on different model architectures, including the Transformer-based Vision Transformer (ViT-T/16) and the ALBERT-Base model for natural language processing. The table compares the performance of three methods: a standard deep ensemble, a deep ensemble enhanced with Sharpness-Aware Minimization (SAM), and the proposed SharpBalance method. The performance metric used is ensemble test accuracy, evaluated on CIFAR100, CIFAR100-C (a corrupted version of CIFAR100), and the MRPC (Microsoft Research Paraphrase Corpus) dataset, respectively. The results demonstrate that SharpBalance consistently outperforms both baseline methods.
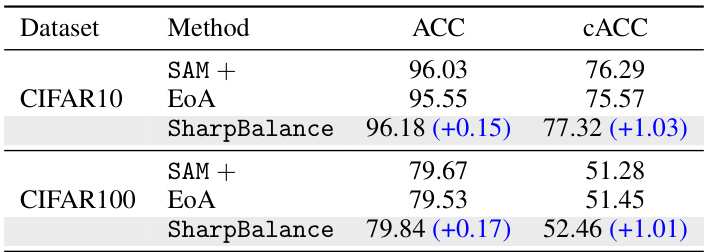
This table compares the performance of SharpBalance against two strong baselines, EoA and SAM+, on CIFAR10 and CIFAR100 datasets. The results demonstrate that SharpBalance achieves superior performance in both in-distribution (ACC) and out-of-distribution (cACC) generalization compared to the baselines.
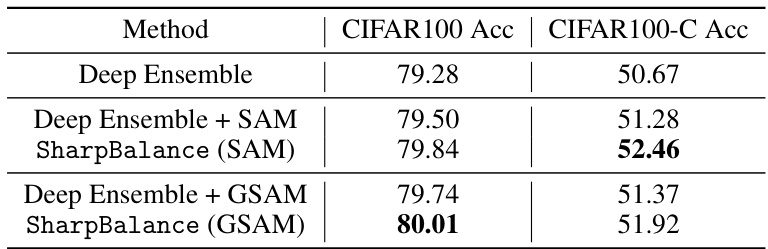
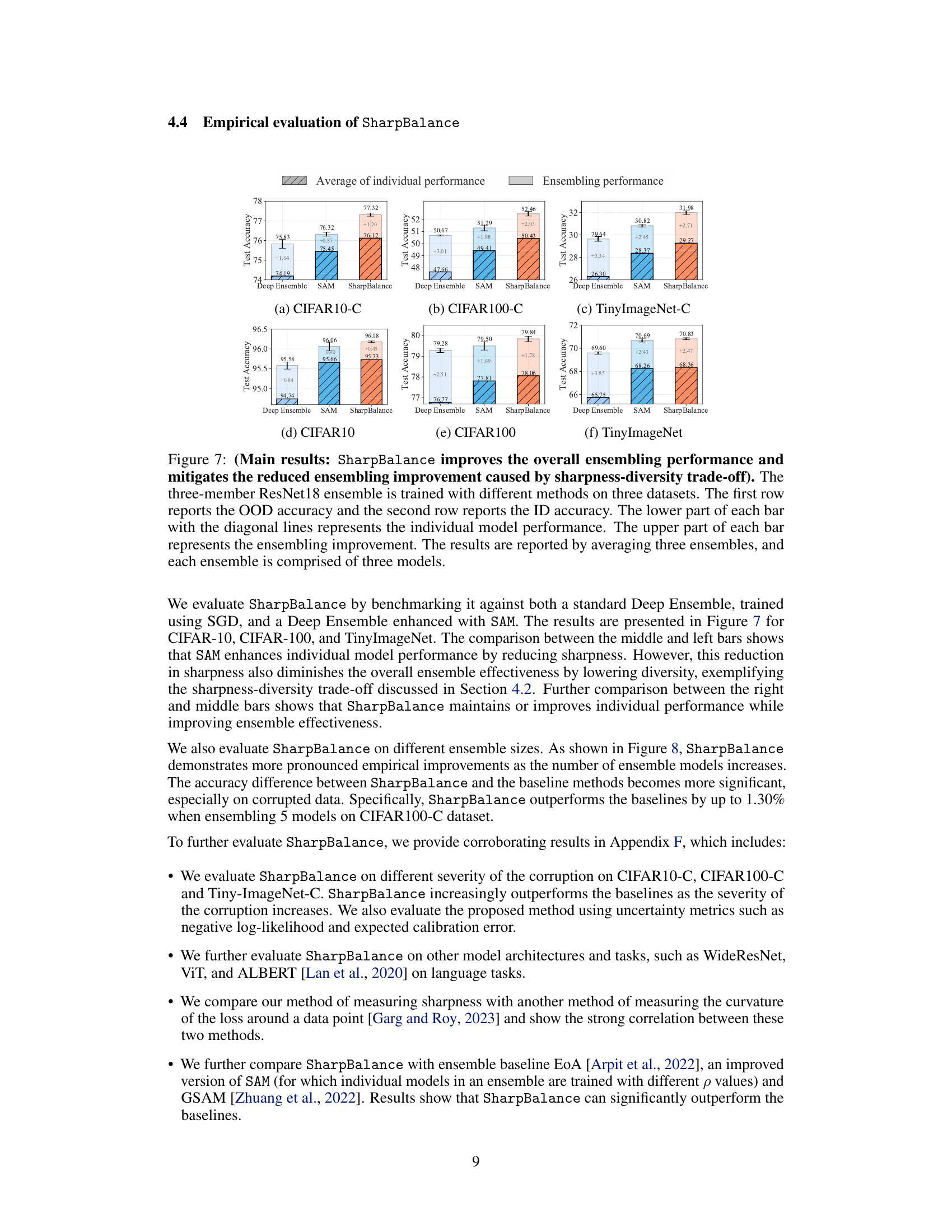
This table shows the results of comparing three different training methods (Deep Ensemble, Deep Ensemble + SAM, and SharpBalance) on three datasets (CIFAR10, CIFAR100, and TinyImageNet) with their corrupted versions. The results are presented as the average of three ensembles, each composed of three models. For each dataset and training method, both in-distribution (ID) accuracy and out-of-distribution (OOD) accuracy are provided. The table illustrates that SharpBalance consistently improves the ensemble performance in both ID and OOD settings.

This table shows the hyperparameters used in the experiments described in Section 4.4 of the paper. It lists the optimal perturbation radius (p) and top-k% threshold for the SharpBalance method, obtained through a grid search. Also included are the datasets used (CIFAR10, CIFAR100, and TinyImageNet), the model architecture (ResNet18), and the methods compared (Deep Ensemble, Deep Ensemble + SAM, and SharpBalance). The random seeds used for averaging the results are also provided.
Full paper#