TSDS: Data Selection for Task-Specific Model Finetuning

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it addresses the critical challenge of data selection for efficient finetuning of large language models. It proposes a novel framework, TSDS, that significantly improves the performance of finetuned models compared to existing methods. This work opens avenues for research in data-efficient machine learning and optimization techniques for large datasets. The efficient algorithms presented also have practical implications for real-world applications.

Visual Insights

#

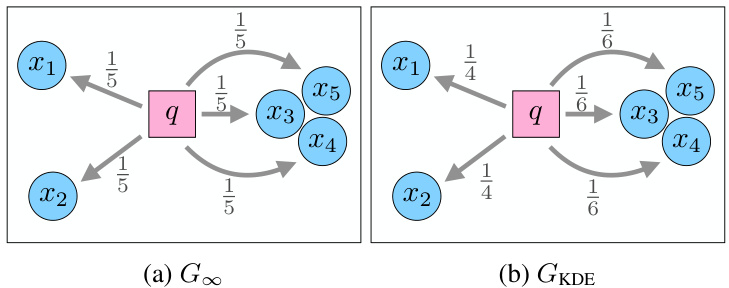
This figure illustrates the difference in optimal probability mass transport between two regularization functions, G∞ and GKDE. In (a), G∞ distributes the probability mass uniformly, regardless of density. However, in (b) GKDE considers the density of the candidates, assigning lower probability to clustered, high-density candidates and higher probability to more distinct examples. This demonstrates GKDE’s robustness to near-duplicate data.

This table presents information about the datasets used for instruction tuning in the TSDS paper. It includes the dataset name, the type of task (Multilingual QA, Multiple choice, Reasoning), the number of test instances, the number of query examples, the number of shots (number of QA examples provided in the prompt), and the evaluation metric used (F1 score or Accuracy). This table helps to understand the experimental setup and the evaluation metrics used in the paper’s experiments on task-specific instruction tuning.

In-depth insights

#

TSDS Framework

#

The TSDS framework, as described in the research paper, presents a novel approach to data selection for task-specific model finetuning. Its core innovation lies in formulating data selection as an optimization problem, leveraging optimal transport to align the selected data distribution with the target task distribution, represented by a small set of example data. This addresses the challenge of efficiently selecting relevant data from massive datasets typical of modern machine learning. The framework incorporates a diversity regularizer, using kernel density estimation to mitigate the negative effects of near-duplicate data points, thus enhancing the model’s generalization ability. Efficient algorithms based on approximate nearest neighbor search are employed to compute the optimal solution, addressing scalability concerns. The TSDS framework’s effectiveness is demonstrated through experiments on instruction tuning and continued pretraining, showing consistent improvements over baseline methods and even surpassing the performance of using the full dataset in certain cases. The framework’s robustness to near-duplicates and its efficiency are also highlighted as significant advantages.

Optimal Transport

#

Optimal transport (OT) is a mathematical framework for efficiently comparing probability distributions. The core idea is to find the minimum-cost way to transform one distribution into another, where the cost is typically a distance metric between points in the underlying spaces. This method is particularly useful in the context of data selection because it quantifies the discrepancy between the distribution of the selected data and the desired target distribution. Distribution alignment, a critical factor in effective model finetuning, is directly addressed by minimizing the OT cost. The approach’s power is in its ability to handle complex relationships between data points, going beyond simple distance comparisons and capturing more nuanced similarities. The practical application involves solving an optimization problem, often computationally intensive; however, the paper introduces efficient algorithms leveraging approximate nearest neighbor search, making OT a viable method for large-scale datasets. Regularization techniques further improve results by ensuring diversity in the selected data and mitigating negative effects from near-duplicates, enhancing the overall robustness and efficiency of the data selection process. In essence, OT provides a rigorous and practical framework for data-driven model fine-tuning.

KDE Regularization

#

The KDE regularization technique, employed to enhance the diversity of data selection in the TSDS framework, addresses the shortcomings of standard regularization methods when dealing with near-duplicate data points. By incorporating kernel density estimation (KDE), the method effectively mitigates the over-sampling of near-duplicates. KDE estimates the probability density of each candidate example, penalizing the selection of highly similar examples based on their density score. This crucial step allows for the selection of a more diverse subset, preventing the model from overfitting to redundant information and improving the overall robustness and generalization of the finetuned model. The integration of KDE offers a significant advantage over techniques that ignore near-duplicates, which can negatively impact performance and create biased models. This novel approach allows for a more robust and efficient data selection process. The effectiveness of KDE regularization is empirically validated, demonstrating consistent performance across various duplication levels showing its practical application in real-world datasets.

Efficiency Analysis

#

An efficiency analysis of a data selection method for fine-tuning foundation models would likely examine several key aspects. First, computational complexity needs a thorough investigation, assessing the scaling behavior with respect to the size of the data repository and the number of query examples. This would involve analyzing the time complexity of the core algorithms (e.g., nearest neighbor search, optimal transport calculations). Second, empirical runtime measurements across varied datasets and hardware configurations would provide concrete evidence of real-world performance. Third, the analysis must consider space complexity, evaluating memory usage for storing intermediate data structures and models. Finally, a discussion on the trade-offs between efficiency and the quality of data selection is crucial. While a faster method might exist, it may compromise the performance of the downstream task. Therefore, the analysis should quantify this trade-off, perhaps by providing a Pareto frontier illustrating different performance-efficiency combinations.

Near-duplicate Robustness

#

The concept of ‘Near-duplicate Robustness’ in data selection for fine-tuning language models is crucial. Standard diversity-promoting regularizers often fail when faced with numerous near-duplicates, which skew the selection process. The paper addresses this by integrating kernel density estimation (KDE) into the regularization term. This modification cleverly penalizes the over-selection of near-duplicates by weighting the probability assignment inversely proportional to their density. This nuanced approach ensures that the selected data remains diverse even when the source dataset contains a high percentage of near-duplicates. The effectiveness of this method is demonstrated through empirical results showing consistent performance in spite of increasing numbers of near-duplicates, a significant improvement over simpler, non-robust approaches.

More visual insights

#

More on figures

This figure illustrates the difference in probability mass transport between two regularization functions: G∞ and GKDE. In the G∞ scenario, probability mass is distributed uniformly to the nearest neighbors regardless of their density. In the GKDE scenario, the clustered candidates (x3, x4, x5), representing near-duplicates, receive less probability mass than the distinct candidates (x1, x2) because GKDE accounts for density, preventing oversampling of near-duplicates.

This figure illustrates the difference in probability mass transport between two regularization functions: G∞ and GKDE. In the G∞ case (left), probability mass is distributed uniformly among the nearest neighbors, without considering density. The GKDE case (right) shows that probability mass is assigned inversely proportionally to the density, preventing over-sampling of clustered, near-duplicate candidates.

More on tables

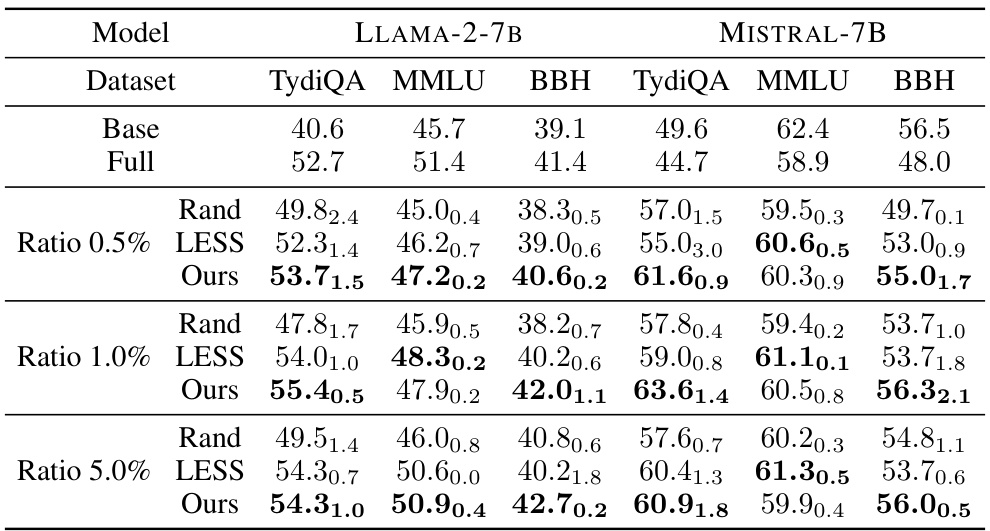
This table presents the results of instruction tuning experiments comparing three data selection methods: Rand (random selection), LESS (state-of-the-art gradient similarity-based selection), and the proposed TSDS method. The performance (F1 score and accuracy) of two language models (LLAMA-2-7B and MISTRAL-7B) is evaluated on three tasks (TydiQA, MMLU, and BBH) with different data selection ratios (0.5%, 1.0%, 5%). The ‘Base’ row shows the performance without finetuning, and the ‘Full’ row shows the performance using the full dataset. The subscripts indicate standard deviations across three runs for each setting.

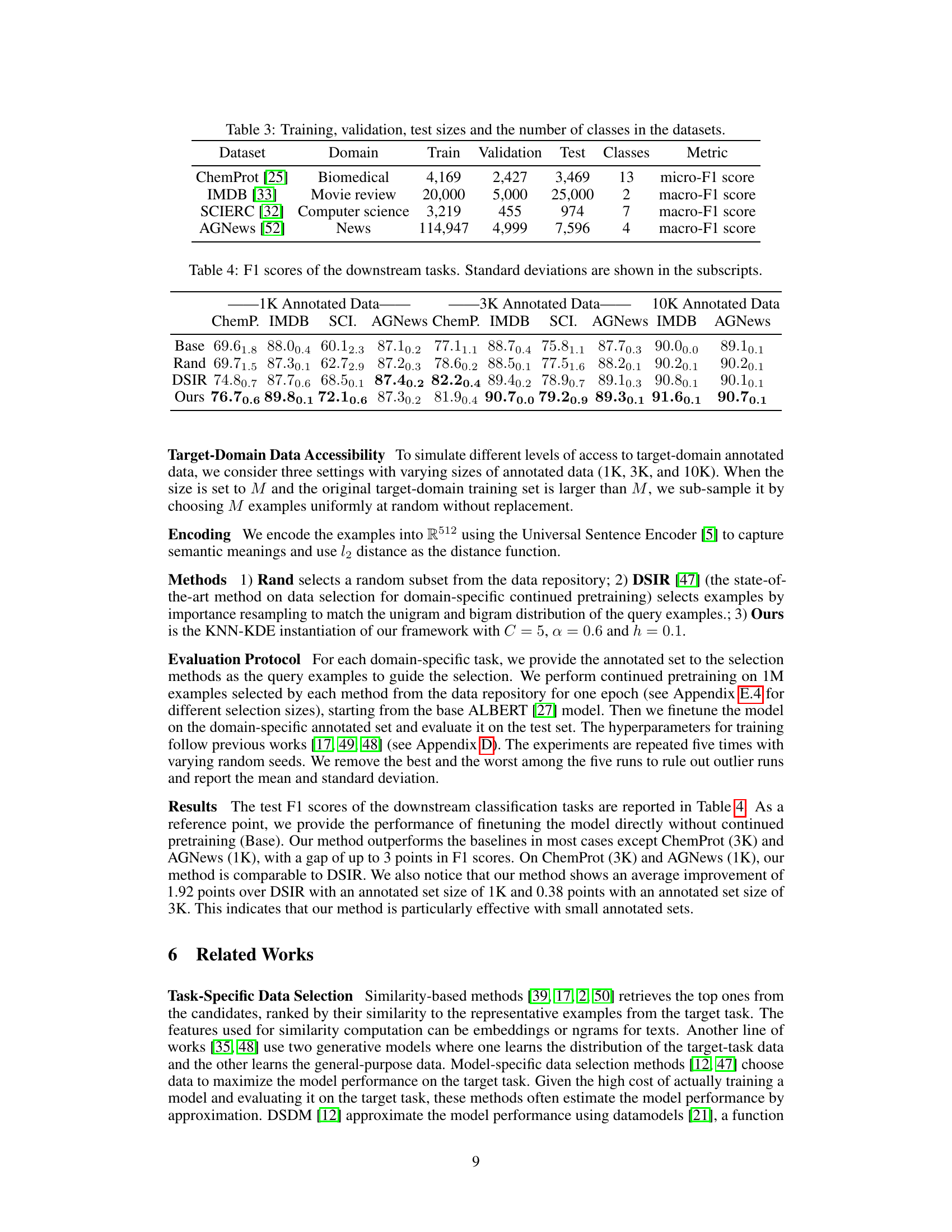
This table presents the sizes of the training, validation, and test sets, along with the number of classes, for four different datasets used in the domain-specific continued pretraining experiments. The datasets represent diverse domains, including biomedical, movie reviews, computer science, and news articles. The metrics used for evaluating performance are also listed.

This table presents the results of instruction tuning experiments comparing three data selection methods: Random sampling, LESS (a state-of-the-art method), and the proposed TSDS method. The performance is measured by F1 score (TydiQA) and accuracy (MMLU, BBH) across three different datasets (TydiQA, MMLU, BBH) and three selection ratios (0.5%, 1%, 5%). The table shows the average performance and standard deviation across three runs with different random seeds for each method and selection ratio, alongside the baseline results for the model without finetuning and with finetuning using the full dataset.

This table presents the results of instruction tuning experiments, comparing the performance of three different data selection methods (Rand, LESS, and Ours) against a baseline (Base) and the full dataset (Full). The comparison is done across three different datasets (TydiQA, MMLU, BBH) and two language models (LLaMA-2-7B and MISTRAL-7B), with varying dataset selection ratios (0.5%, 1%, 5%). The F1 score and accuracy are reported as the evaluation metrics, along with standard deviations to indicate variability.

This table lists the hyperparameters used for the continued pretraining stage of the experiments described in Section 5.2 of the paper. The hyperparameters control various aspects of the training process, including the maximum length of input sequences, batch size, optimizer, weight decay parameters for Adam, warmup ratio, learning rate scheduler, and learning rate.

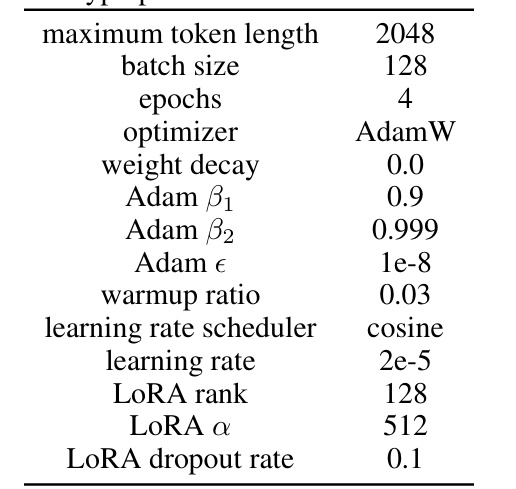
This table compares the performance of the proposed TSDS method with the LESS baseline method for task-specific instruction tuning. The experiment uses a dataset size of 4% of the candidate data repository and trains each model for only one epoch. The table shows F1 scores and accuracy for three different tasks (TydiQA, MMLU, BBH) and two different language models (LLAMA-2-7B and MISTRAL-7B). Subscripts indicate standard deviations.

This table presents the results of instruction tuning experiments, comparing the performance of three different data selection methods against a baseline. The methods are: randomly selecting data, using the LESS method (a state-of-the-art technique), and using the authors’ proposed TSDS method. The table shows F1 scores and accuracy for three different tasks (TydiQA, MMLU, and BBH) across different model sizes and data selection ratios (0.5%, 1%, and 5%). The subscripts indicate standard deviations across three different runs with different random seeds, demonstrating the performance variability of each method.

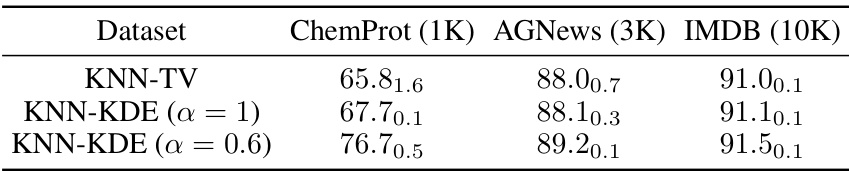
This table presents the results of experiments evaluating the impact of different kernel sizes on the performance of the KNN-KDE method. The F1 scores for three downstream tasks (ChemProt, AGNews, IMDB) are shown, with standard deviations included to indicate the variability of the results. The kernel sizes tested were 0.1, 0.3, and 0.5.

This table presents the F1 scores achieved on four different downstream classification tasks (ChemProt, IMDB, SCIERC, AGNews) using three different data selection methods (Rand, DSIR, Ours) and three different sizes of annotated data (1K, 3K, 10K). The ‘Base’ row shows the performance without data selection or continued pre-training. The table highlights the improvements in F1 score obtained by using the proposed TSDS method compared to baseline methods.

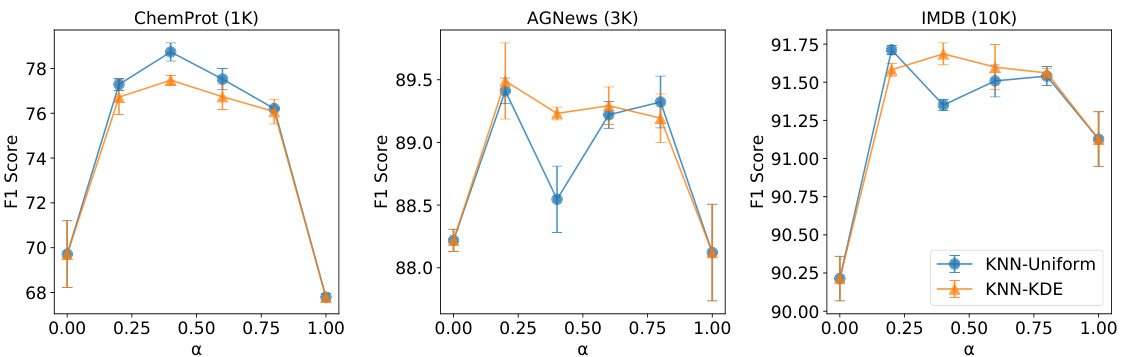
This table shows the average neighborhood size used by the KNN-Uniform and KNN-KDE algorithms for different values of the hyperparameter α. The neighborhood size represents the number of nearest neighbors considered when selecting data for training. The numbers before the slash are the neighborhood sizes for KNN-Uniform, and the numbers after the slash are the neighborhood sizes for KNN-KDE. The results are presented for three different datasets: ChemProt (1K), AGNews (3K), and IMDB (10K).

Full paper

#