↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Crowdsourcing, while cost-effective, often yields noisy labels impacting label integration algorithms. Existing methods typically assume a fixed neighborhood size for each instance, which limits their effectiveness. This is inefficient and inaccurate as instances closer to class centers benefit from larger neighborhoods compared to those on boundaries.
KFNN innovatively addresses this by automatically determining the optimal neighborhood size for each instance. It leverages a Mahalanobis distance distribution to model relationships between instances and classes, enhancing label distributions. A Kalman filter is incorporated to reduce noise from neighbor instances, and max-margin learning optimizes neighborhood sizes. KFNN significantly outperforms existing algorithms across various crowdsourcing scenarios, demonstrating superior accuracy and robustness, particularly when dealing with limited and noisy label data.
Key Takeaways#
Why does it matter?#
This paper is important because it addresses a critical limitation in existing crowdsourced label integration methods. By dynamically adjusting neighborhood size, it enhances accuracy and robustness, particularly relevant in scenarios with limited annotations and noisy labels. This opens avenues for improving efficiency and reliability in various machine learning applications relying on crowdsourcing.
Visual Insights#

This figure compares KFNN’s performance against six other state-of-the-art algorithms on two real-world datasets, Income and Leaves. It shows the Macro-F1 scores and integration accuracies for each algorithm, highlighting KFNN’s superior performance on both datasets.
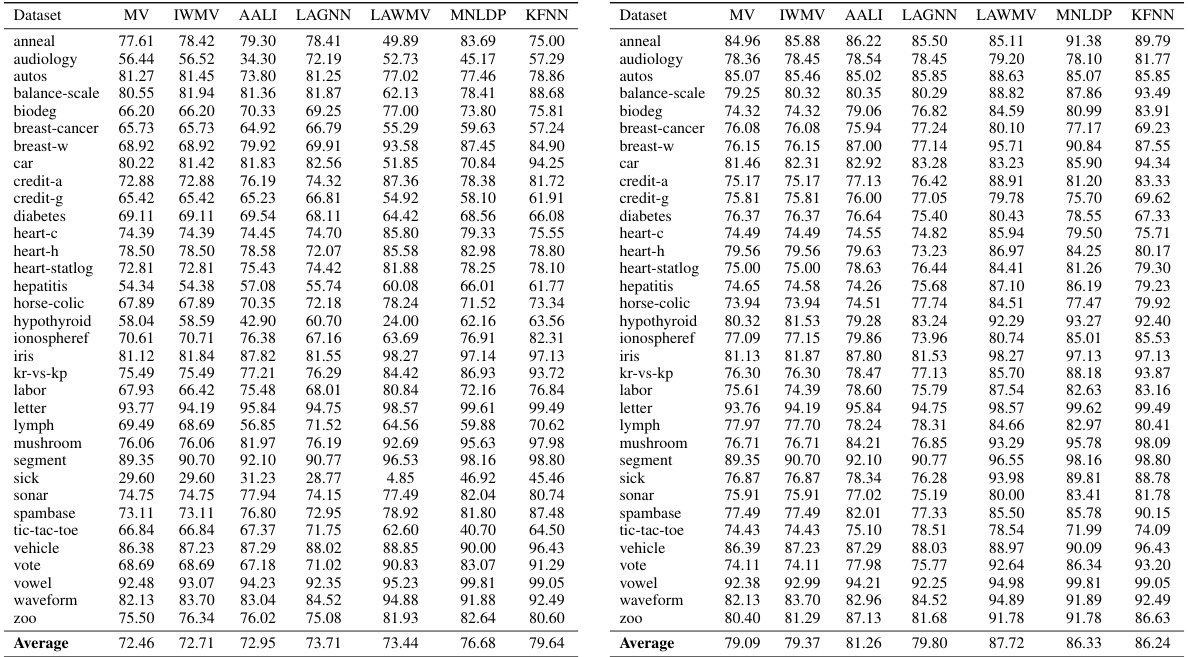
This table presents a comparison of the Macro-F1 scores achieved by KFNN and six other state-of-the-art label integration algorithms across 34 simulated datasets. The Macro-F1 score is a metric that considers both precision and recall, providing a balanced assessment of the algorithm’s performance across different classes. The results show KFNN’s performance relative to other methods, highlighting its effectiveness.
In-depth insights#
KFNN: A Novel Approach#
KFNN, as a novel approach, presents a robust solution to label integration challenges in crowdsourcing. Its core innovation lies in dynamically adjusting neighborhood size for each data instance, unlike existing methods that assume a fixed size. This adaptability is crucial because instances closer to class boundaries benefit from smaller neighborhoods, while those near the center benefit from larger ones. The method leverages Mahalanobis distance to model instance-class relationships and a Kalman filter to mitigate noise from neighbor instances. Max-margin learning optimizes the neighborhood size, further enhancing accuracy. The approach exhibits superior performance and robustness compared to state-of-the-art methods across various scenarios.
Mahalanobis Distance#
The concept of Mahalanobis distance is central to the KFNN algorithm’s ability to adaptively determine optimal neighborhood sizes for each data instance. Unlike Euclidean distance, which treats all features equally, Mahalanobis distance accounts for the covariance between features, providing a more nuanced measure of similarity. This is particularly crucial in handling noisy and heterogeneous crowdsourced data, where feature correlations significantly impact the accuracy of label integration. By modeling the relationship between instances and classes using Mahalanobis distance, KFNN effectively captures the underlying data structure, enabling it to better leverage neighboring instances for label inference. The use of the Mahalanobis distance is a key innovation in KFNN, as it allows for a more robust and accurate estimation of neighborhood size compared to approaches relying on simple Euclidean distance or fixed-size neighborhoods. This results in improved performance in diverse crowdsourcing scenarios.
Kalman Filter Fusion#
The heading ‘Kalman Filter Fusion’ suggests a method for integrating noisy data from multiple sources using a Kalman filter. This technique is particularly relevant in scenarios like crowdsourcing, where multiple annotators provide potentially unreliable labels for the same data point. The core idea likely involves representing the noisy label distributions as state variables within the Kalman filter framework. The filter recursively updates these estimates by incorporating new information, thus mitigating the effect of individual noisy measurements. The key benefits are likely to be improved accuracy and robustness compared to simpler aggregation methods. The effectiveness hinges on the model’s ability to accurately represent noise characteristics and the relationship between data sources. A well-designed Kalman filter fusion method should demonstrate improved performance in noisy and ambiguous settings, potentially by achieving a higher overall classification accuracy or producing more reliable estimations of the true labels. The computational cost is a crucial consideration; Kalman filters can be computationally expensive, especially with high-dimensional data. The design of the state variables and the filter parameters would be key factors influencing the performance of this fusion technique.
K-Free Optimization#
The heading ‘K-Free Optimization’ suggests a method for dynamically determining the optimal neighborhood size (k) in a k-nearest neighbor (KNN) algorithm, breaking away from the traditional fixed-k approach. This is particularly insightful in crowdsourcing scenarios where data quality is variable, and a fixed k may lead to biased results. The approach likely involves a learning-based strategy to adaptively choose k based on instance attributes and label quality, potentially optimizing for maximum margin separation between classes. This dynamic k-selection offers advantages over fixed-k methods by providing greater robustness to noisy data and potentially improved classification accuracy, especially in datasets with varying class densities or imbalanced class representation. The ‘free’ aspect implies that each instance is not constrained by a pre-determined neighborhood size, resulting in a more flexible and data-driven model that better adapts to the unique characteristics of each data point within the crowdsourced dataset. The specific optimization technique employed (e.g., max-margin learning, Kalman filtering) would further clarify the innovative aspect of the proposed method.
Future Work#
The paper’s conclusion mentions several promising avenues for future research. Improving the robustness of the KFNN algorithm is a key area, particularly addressing the sensitivity to the parameters (\alpha) and (\beta) in the Kalman filter. A more adaptive mechanism for these parameters, potentially learned from data, would enhance the algorithm’s performance across various datasets. Refining the max-min normalization used to transform the distance distribution into a potential label distribution is also suggested. Exploring alternative distance metrics or transformations better suited for different data types could significantly improve the algorithm’s generalization capabilities. Finally, the authors highlight the need for more sophisticated methods to address the challenges of handling missing data and noisy labels, especially in imbalanced datasets. Investigating more advanced imputation techniques or exploring more robust loss functions are worthwhile considerations for future improvements.
More visual insights#
More on figures

This figure shows the impact of hyperparameters α and β on the performance of KFNN using Macro-F1 scores. It illustrates the sensitivity of KFNN to different values of α and β for two datasets, Income and Leaves. The x-axis represents α, the y-axis represents β, and the z-axis shows the Macro-F1 score. This visualization helps understand the optimal values for α and β to achieve better performance on the KFNN model.
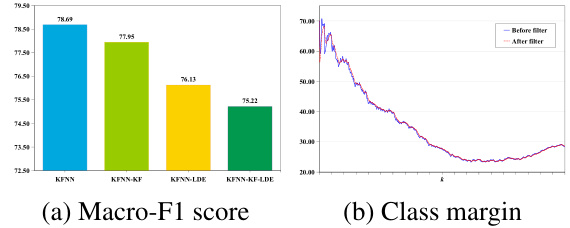
This figure shows the ablation study of KFNN. It compares the performance of KFNN with three variants: KFNN-KF (without K-free optimization), KFNN-LDE (without label distribution enhancement), and KFNN-KF-LDE (without both). The Macro-F1 score is shown in (a), indicating that both components are important for KFNN’s performance. The class margin is shown in (b), illustrating the impact of the Kalman filter in mitigating noise from neighbor instances.
More on tables

This table presents the results of Wilcoxon signed-rank tests comparing KFNN’s performance against other state-of-the-art label integration algorithms. The ‘+’ symbol indicates that KFNN significantly outperforms the algorithm in the column, ‘o’ indicates the opposite, and a blank indicates no significant difference. The significance levels are α = 0.05 and α = 0.1 for the lower and upper diagonals, respectively. This table helps to establish the statistical significance of KFNN’s superior performance.

This table lists the characteristics of 34 simulated datasets used in the paper’s experiments. For each dataset, it shows the number of instances, the number of attributes, the number of classes, whether the dataset contains missing values, and the type of attributes (nominal, numeric, hybrid). These datasets represent various crowdsourcing scenarios and are used to evaluate the performance of the proposed KFNN algorithm against existing methods.
Full paper#