↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multiobjective Optimization (MOO) faces the challenge of generating a diverse and representative set of Pareto-optimal solutions. Existing methods often lack formal definitions of representability and uniformity, hindering the generation of high-quality solution sets. Furthermore, directly optimizing for minimal fill distance (a measure of solution representativeness) is computationally intractable.
This paper introduces UMOD, a novel method that addresses these issues. UMOD uses a surrogate objective function, maximizing the minimal pairwise distances among solutions, which provides a good approximation of the optimal design that minimizes fill distance. The method employs a bi-level optimization framework with neural network approximation for efficient computation. Extensive empirical results on synthetic and real-world benchmarks demonstrate that UMOD efficiently produces high-quality, representative solutions and outperforms state-of-the-art methods.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in multiobjective optimization because it introduces a novel uniformity metric and an efficient algorithm for generating high-quality, representative Pareto-optimal solutions. It addresses a critical challenge in MOO, improving the representativeness and diversity of solution sets. The proposed framework opens up new avenues for research on design optimization problems. This work offers valuable insights and practical tools for researchers working on a wide range of application domains where generating diverse and uniformly distributed solutions is critical.
Visual Insights#

This figure illustrates the concept of covering a Pareto Front (PF) with a set of uniformly distributed Pareto objectives. The Pareto Front represents the set of optimal solutions in a multi-objective optimization problem, where it’s impossible to improve one objective without worsening another. The figure shows eight points (Pareto objectives) that uniformly cover the curved PF, with circles representing the distance each point covers (covering radius). A small covering radius indicates that the set of points effectively represents the entire Pareto Front, which is desirable in multi-objective optimization.
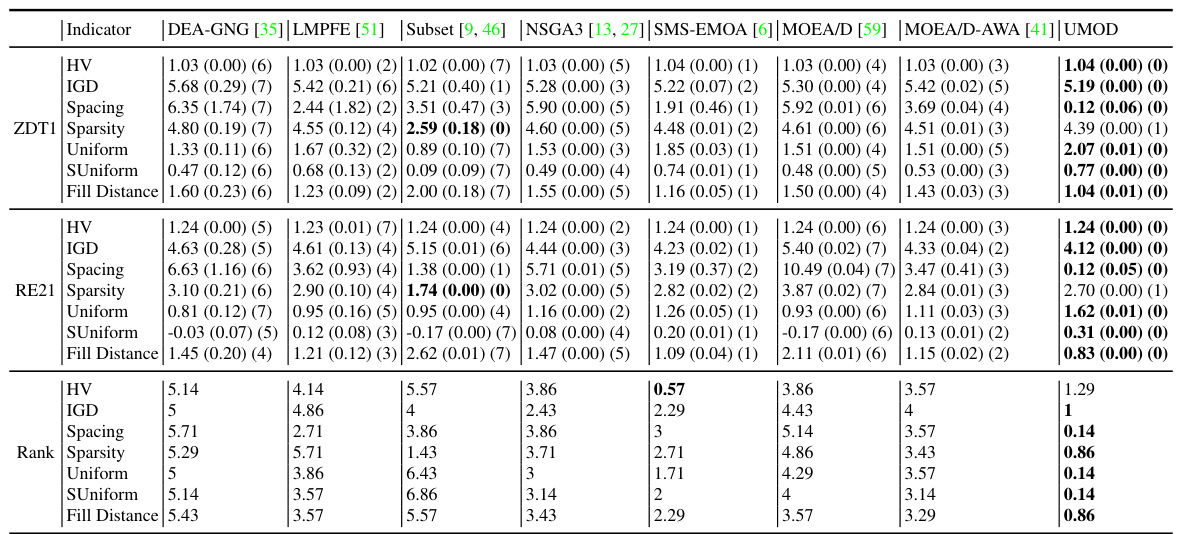
This table presents partial results for several biobjective problems, comparing the performance of different multi-objective optimization algorithms. The algorithms are evaluated based on various metrics such as Hypervolume (HV), Inverted Generational Distance (IGD), Spacing, Sparsity, Uniformity, Soft Uniformity, and Fill Distance. The full results for these metrics are available in Table 7.
In-depth insights#
Uniform Pareto Front#
A uniform Pareto front signifies an even distribution of Pareto optimal solutions across the objective space, maximizing diversity and representativeness. Non-uniform fronts, in contrast, might cluster solutions in certain areas, leaving others under-represented. Achieving uniformity is crucial for effective decision-making as it ensures a comprehensive exploration of trade-offs, avoids bias towards specific regions of the solution space, and facilitates a fairer comparison of alternatives. Methods for generating uniform Pareto fronts often involve sophisticated optimization strategies, aiming to minimize the distance between adjacent solutions while maintaining Pareto optimality. This challenge is further compounded by the often complex and non-convex nature of Pareto fronts in real-world problems. The choice of a uniformity metric is also critical, influencing the design and evaluation of solution generation algorithms. The pursuit of a truly uniform Pareto front frequently requires a balance between computational efficiency and the quality of the resultant distribution.
Fill Distance Metric#
The concept of a fill distance metric, in the context of multi-objective optimization and Pareto front representation, offers a quantitative measure of how well a discrete set of Pareto-optimal solutions covers the entire Pareto front. Unlike qualitative assessments of diversity, fill distance provides a precise mathematical definition, enabling a rigorous analysis of solution distribution. It’s particularly useful in evaluating the representativeness of a given set of solutions, ensuring that the selected solutions capture the full spectrum of Pareto optimal points and do not unduly concentrate in certain regions. However, directly optimizing for minimal fill distance is computationally challenging due to the nested nature of the optimization problem. This motivates the exploration of surrogate objectives, which are more computationally tractable and provide bounds on the optimal fill distance, thus enabling the efficient discovery of high-quality, well-distributed sets of Pareto-optimal solutions.
UMOD Algorithm#
The UMOD algorithm, presented in the context of multi-objective optimization, is a novel approach to generating a diverse and representative set of Pareto-optimal solutions. Its core innovation lies in using fill distance as a metric to quantitatively assess the uniformity and quality of the generated solutions, addressing a key limitation of prior methods that lacked formal definitions of representability. UMOD cleverly sidesteps the computational intractability of directly minimizing fill distance by proposing a surrogate objective function: maximizing the minimal pairwise distances among the selected solutions. This surrogate is easier to optimize, asymptotically converging to a uniform measure over the Pareto front while theoretically bounding the fill distance within a factor of 4 of the minimum. The algorithm incorporates a bi-level optimization strategy, using neural networks to approximate the Pareto front and efficiently solve the max-min problem. Experimental results on both synthetic and real-world benchmarks demonstrate UMOD’s efficiency and ability to generate high-quality solutions that outperform baseline methods, particularly in terms of uniformity metrics.
Fairness Classification#
In the realm of machine learning, fairness is paramount. Fairness classification tackles the challenge of creating models that make unbiased predictions, avoiding discriminatory outcomes. This is particularly crucial when dealing with sensitive attributes like race, gender, or socioeconomic status. The research delves into methods for optimizing fairness metrics alongside accuracy, often framing this as a multi-objective optimization problem. The goal is not to simply improve accuracy, but to achieve a balance between accuracy and fairness, finding a Pareto optimal set of solutions representing diverse trade-offs. Algorithmic approaches are central; evolutionary algorithms and gradient-based methods are common tools for navigating this complex optimization landscape, searching for solutions that satisfy multiple, often conflicting objectives. Measuring fairness is key; different metrics (like equal opportunity or demographic parity) capture various aspects of fairness, allowing researchers to explore trade-offs. The ultimate objective is to develop and refine algorithms that produce highly accurate models while actively mitigating bias and promoting equitable outcomes for all individuals. This involves dealing with potential challenges such as dataset biases and handling the often non-convex nature of the underlying optimization problems.
Future Research#
Future research directions stemming from this work could explore several promising avenues. Extending UMOD to handle a wider variety of MOPs is crucial, including those with discrete variables, constraints, or disconnected Pareto fronts. Investigating the impact of different neural network architectures and training methods on UMOD’s performance and efficiency is also important. A deeper theoretical analysis connecting fill distance, IGD, and other uniformity metrics could provide valuable insights into the fundamental properties of uniform Pareto designs. Furthermore, applying UMOD to large-scale real-world problems across diverse domains such as materials science, drug discovery, and resource management will demonstrate practical impact and reveal new challenges. Finally, exploring the potential of combining UMOD with other MOO techniques for enhanced performance is a worthwhile direction.
More visual insights#
More on figures
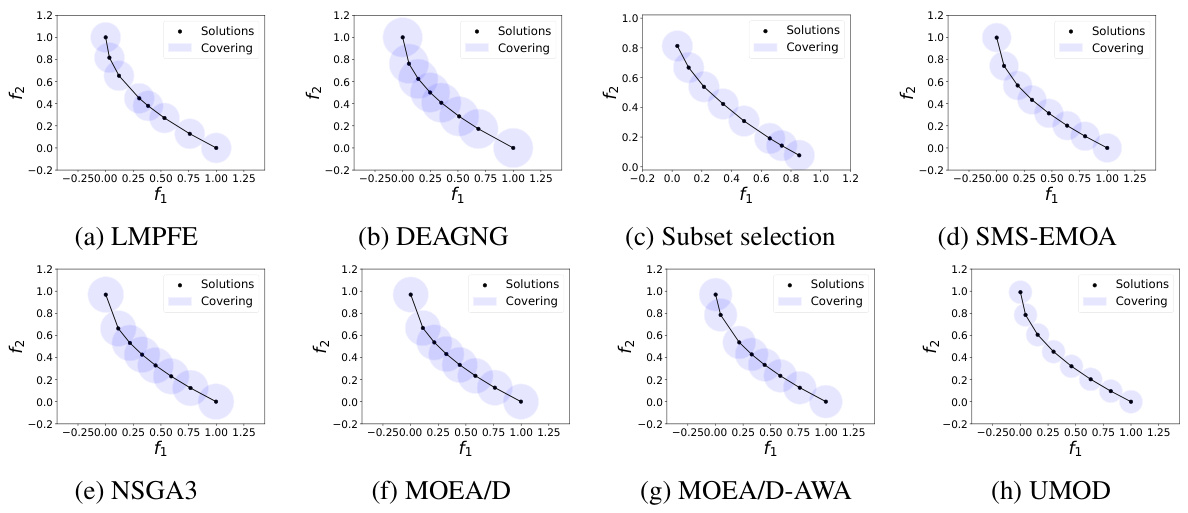
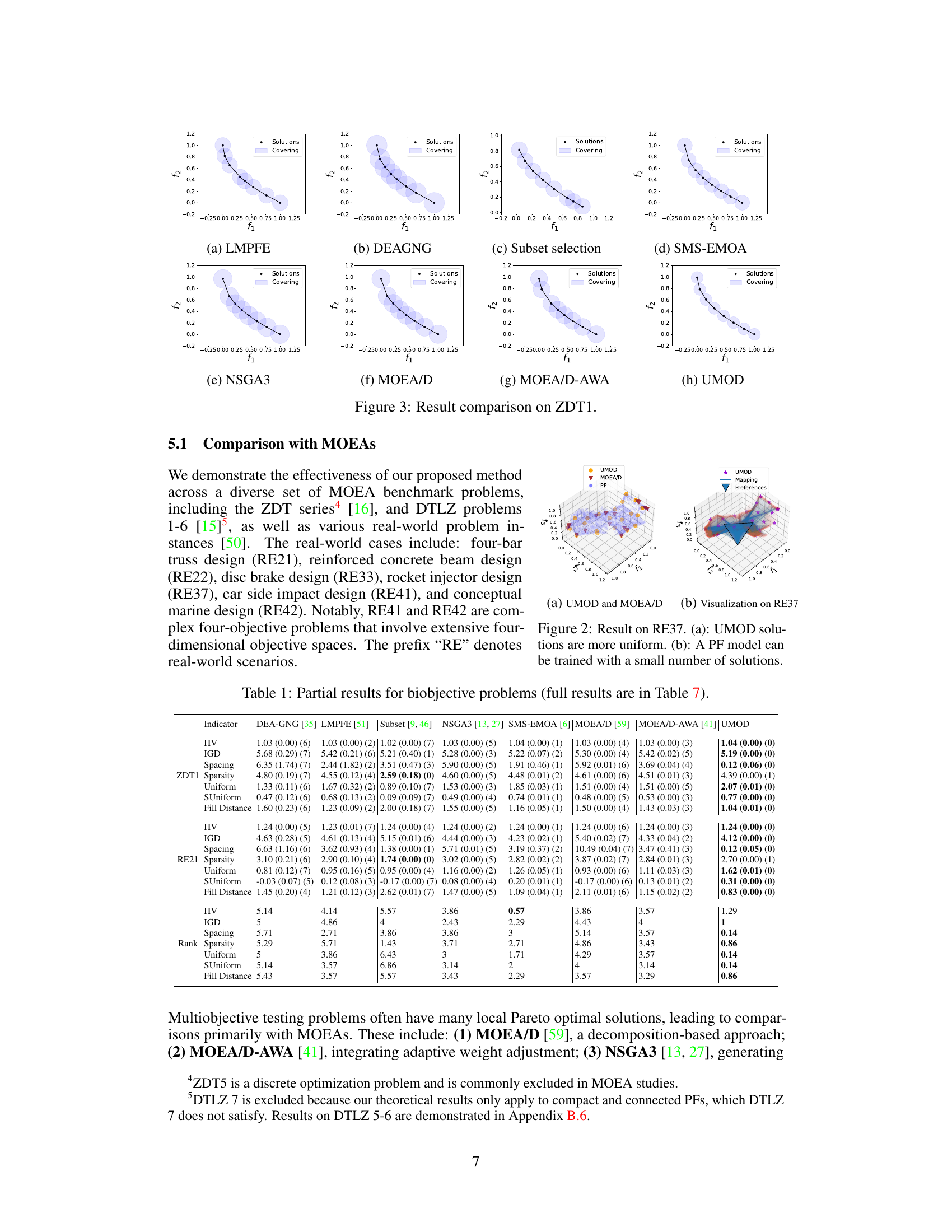
The figure shows the result comparison on ZDT1 of eight different multi-objective optimization methods, including LMPFE, DEAGNG, Subset selection, SMS-EMOA, NSGA3, MOEA/D, MOEA/D-AWA, and UMOD. Each method’s result is visualized in a separate subplot. The subplots show the Pareto front (PF) along with the obtained Pareto objectives (solutions). The size and distribution of the solutions help visualize the quality and uniformity of each method in finding Pareto solutions.
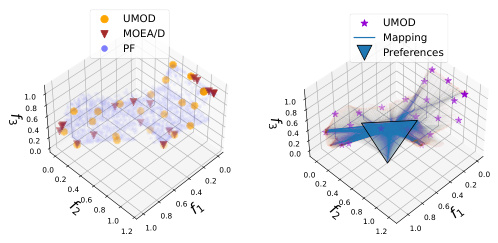
This figure compares the performance of UMOD and MOEA/D on two different problems: RE21 (a real-world problem) and DTLZ2 (a synthetic problem). The left panel shows the solutions obtained by UMOD and MOEA/D for RE21 in the objective space, highlighting the superior uniformity of UMOD’s results. The right panel presents additional visualizations, including the mapping of preferences to the Pareto front (PF) for UMOD, indicating how the method achieves a uniform distribution of solutions by effectively covering the entire Pareto front.

This figure compares the performance of UMOD and MOEA/D on the RE21 and DTLZ2 benchmark problems. Subfigure (a) shows the distribution of solutions generated by UMOD on RE21, demonstrating a uniform coverage of the Pareto front. Subfigure (b) shows the solution distribution of MOEA/D on the same problem, highlighting a less uniform distribution, especially with clustering at the boundaries. Subfigure (c) provides a 3D visualization of the Pareto front comparison between the two methods, again showing UMOD’s more uniform spread. Finally, subfigure (d) plots the minimal distances to other objectives for each method, quantitatively demonstrating UMOD’s achievement of larger minimal pairwise distances, indicating better uniformity.

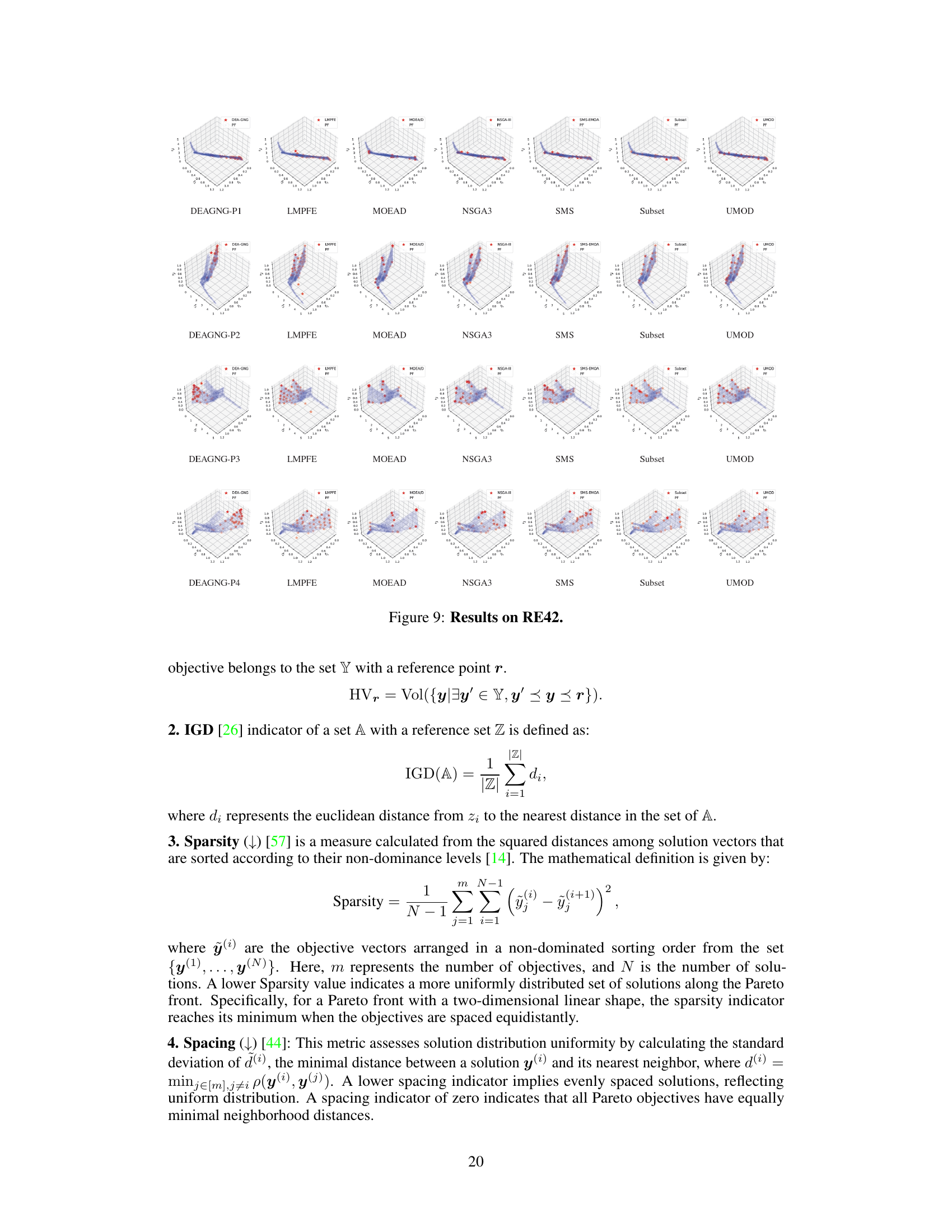
This figure visualizes the Pareto front obtained by different multi-objective optimization methods on the RE41 benchmark problem. It shows the distribution of solutions projected onto different three-dimensional subspaces of the four-dimensional objective space. The methods compared include DEA-GNG, LMPFE, Subset Selection, and UMOD. The visualization highlights the differences in the uniformity and coverage of the Pareto front achieved by each method, with UMOD demonstrating superior uniformity and coverage compared to others.
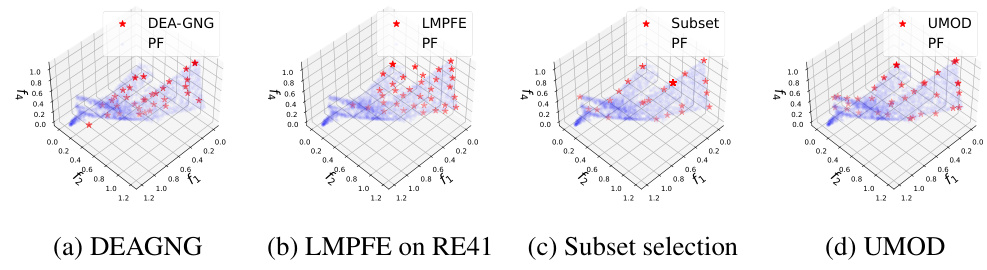
This figure compares the performance of four different multi-objective optimization algorithms (DEAGNG, LMPFE, Subset selection, and UMOD) on the RE41 problem. Each subfigure shows a 3D projection of the Pareto front obtained by each algorithm, along with the true Pareto front. The visualization helps illustrate how well each algorithm approximates the true Pareto front, highlighting differences in distribution and coverage of the optimal solutions.
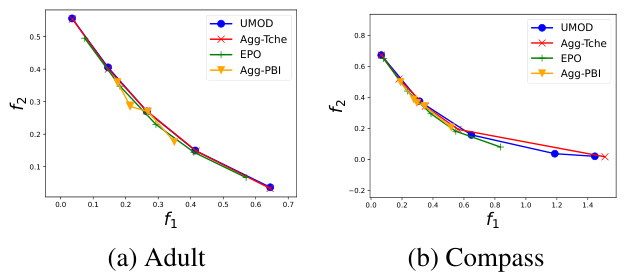
The figure visualizes the Pareto fronts obtained by different methods on two fairness classification datasets, Adult and Compass. The x-axis represents the accuracy, and the y-axis represents the fairness (equality of opportunity). The figure shows that UMOD achieves a more uniformly distributed set of Pareto objectives compared to other methods. This indicates better coverage of the Pareto front, reflecting a balance between accuracy and fairness.
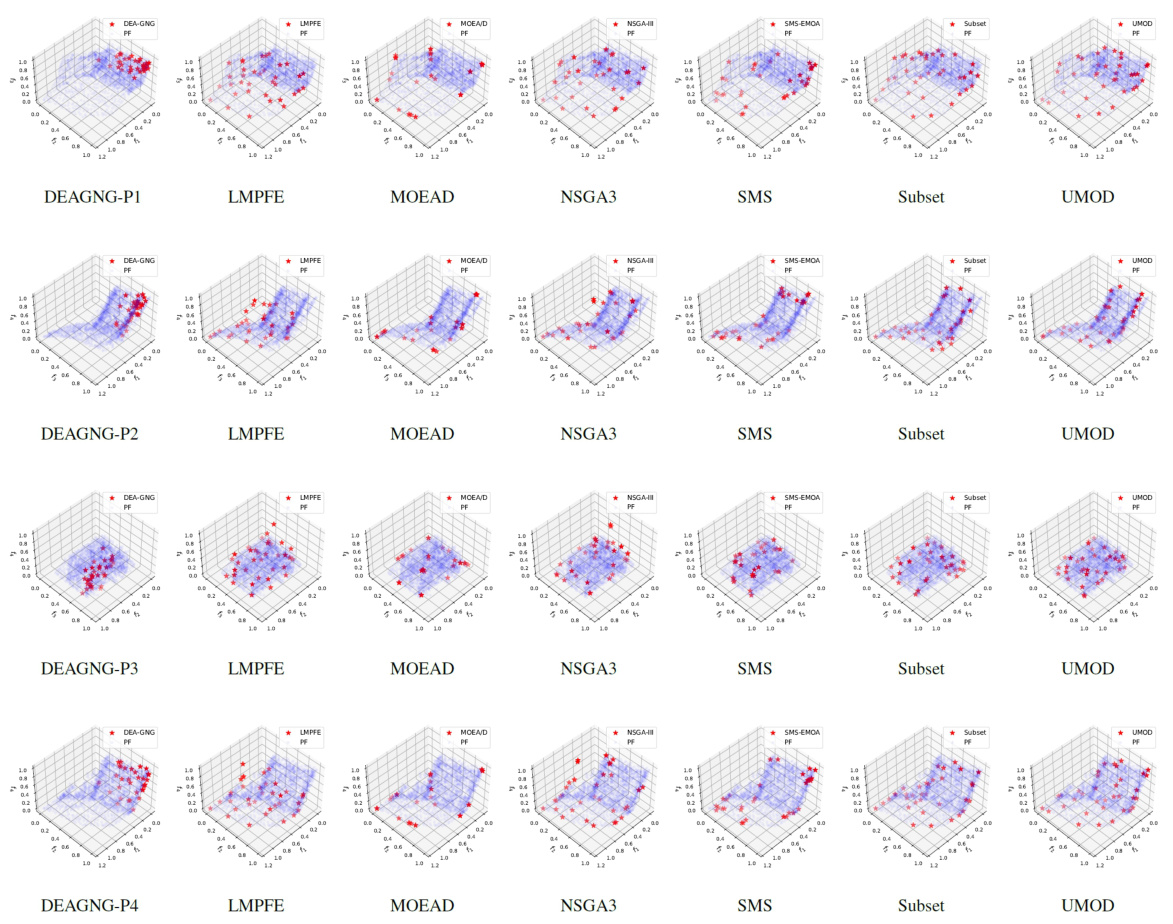
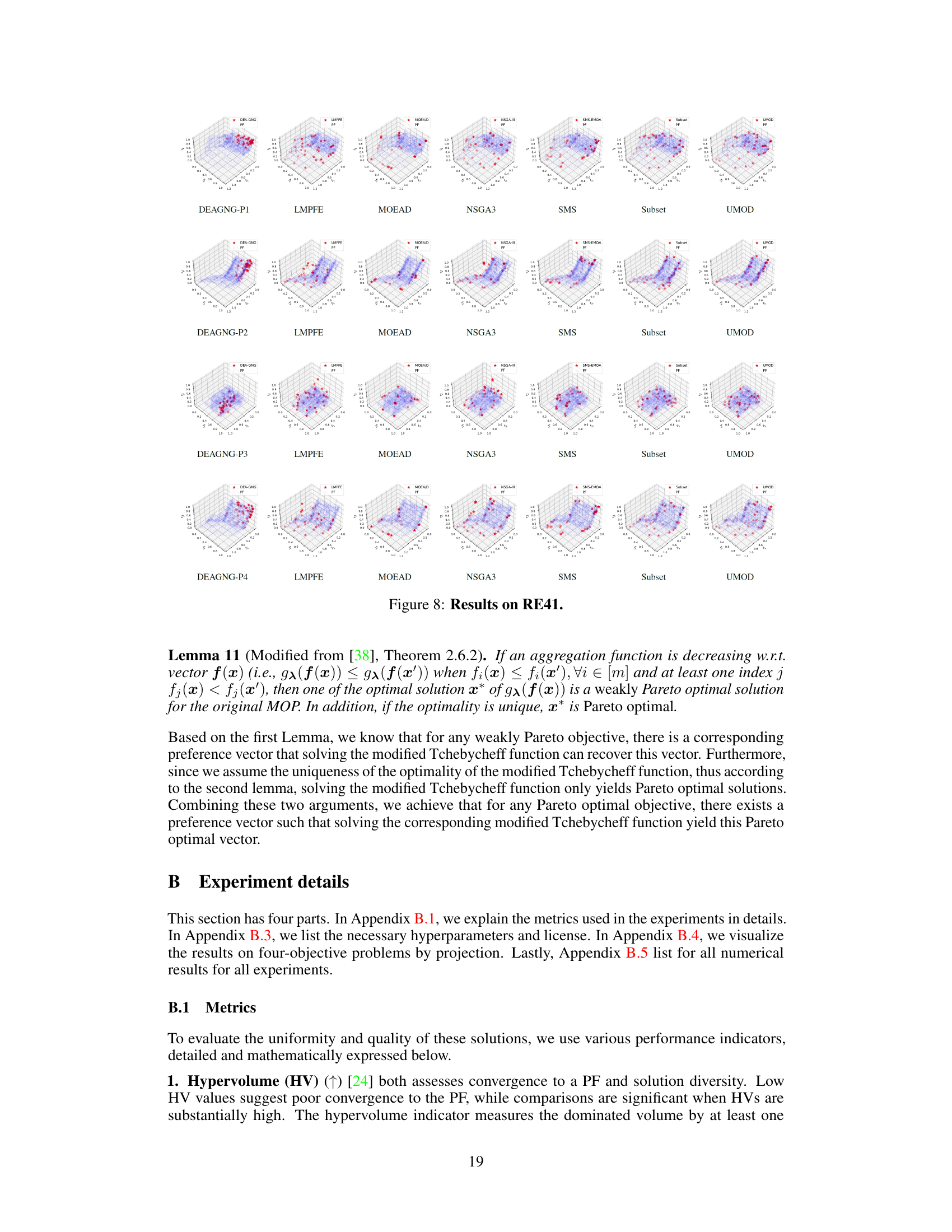
This figure visualizes the results of the proposed UMOD method and other baseline methods on the RE41 benchmark problem. It shows the distribution of Pareto objectives in four different 3D projections, labeled as P1 to P4. The projections show the performance of each method in covering the Pareto front, with UMOD generally demonstrating more uniform and broader coverage compared to other methods, which exhibit more clustering or sparsely distributed solutions. This visualization helps to demonstrate the superior performance of UMOD in generating uniformly distributed Pareto objectives.
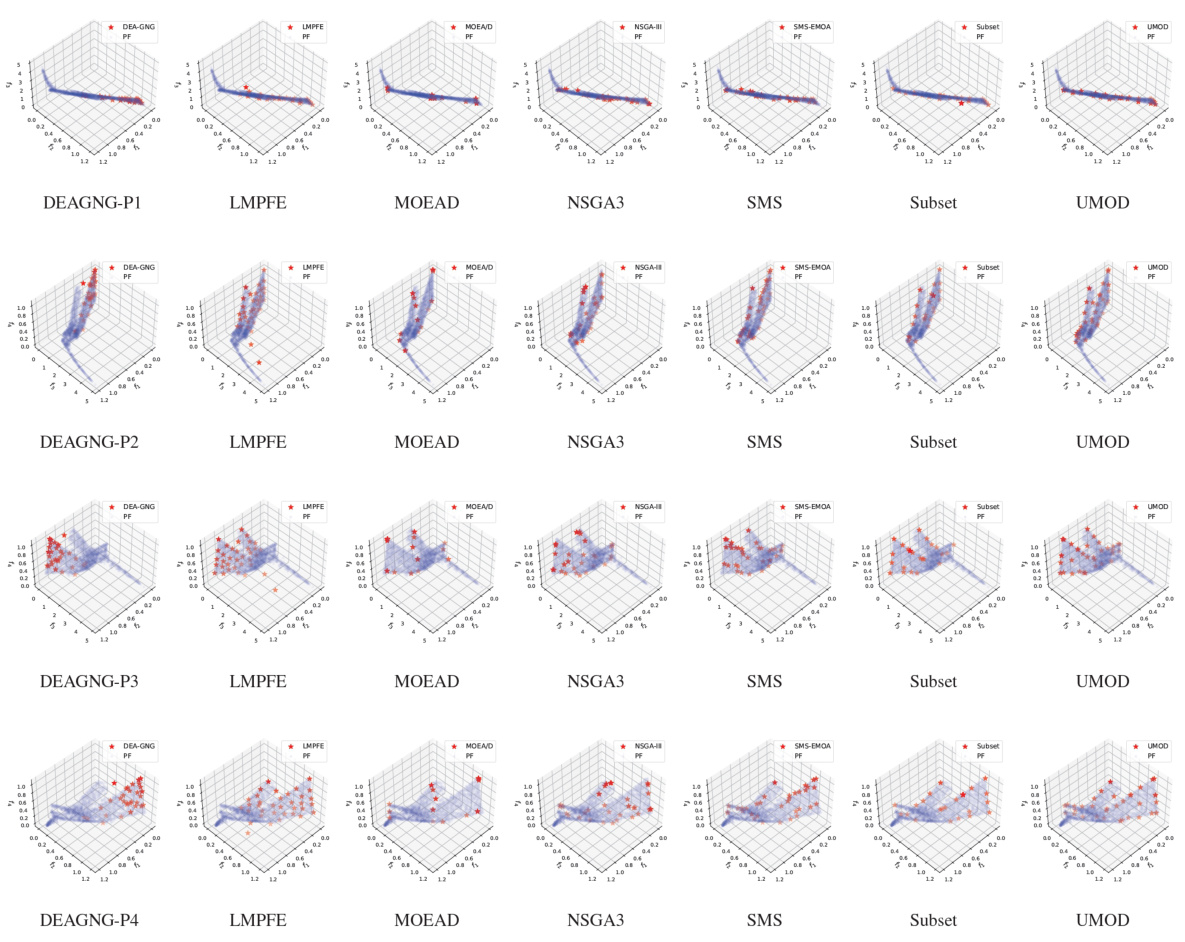
This figure visualizes the results of the proposed UMOD method and several other multi-objective optimization methods on the RE41 problem (a real-world four-objective problem). It shows the Pareto front approximations projected onto different three-dimensional subspaces of the four-dimensional objective space. The visualizations help to compare the uniformity and coverage of the different methods. UMOD generally shows a more uniformly distributed set of solutions covering a larger portion of the true Pareto front compared to other methods.
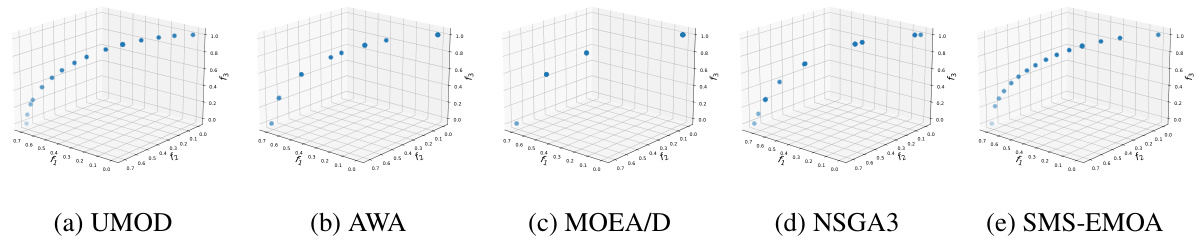
This figure compares the performance of five different multi-objective optimization methods (UMOD, AWA, MOEA/D, NSGA3, and SMS-EMOA) on the DTLZ5 problem. Each subplot shows the Pareto front generated by a different method, visualizing the distribution of Pareto optimal solutions in the three-objective space. The goal is to evaluate how well each method generates a uniformly distributed set of Pareto optimal solutions that represent the entire Pareto front. This problem is particularly challenging because DTLZ5 has a degenerate, one-dimensional hyper-curve as a Pareto front within the three-objective space.

This figure compares the performance of five different multi-objective optimization algorithms (UMOD, AWA, MOEA/D, NSGA3, and SMS-EMOA) on the DTLZ5 problem. Each subfigure shows the distribution of Pareto-optimal solutions obtained by each algorithm in a three-dimensional objective space. This visualization allows comparison of the uniformity and distribution of the generated solutions.

This figure illustrates a scenario where the Tchebycheff aggregation function produces duplicated Pareto optimal solutions. Two different preference vectors, λ(1) and λ(2), both intersect the Pareto front at the same optimal objective vector y*. This occurs because the preference vectors do not intersect the Pareto front at unique points, leading to multiple preference vectors mapping to the same Pareto optimal solution.
More on tables
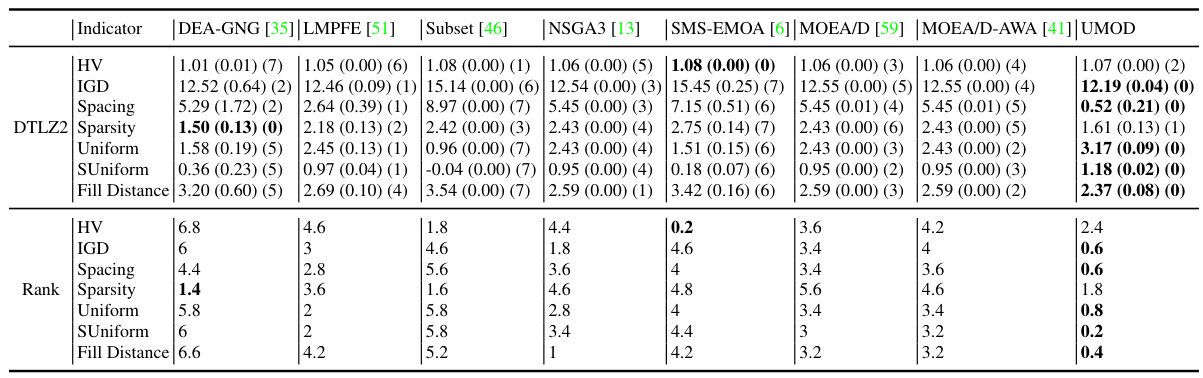
This table shows a subset of the results for biobjective problems. It compares the performance of several multi-objective optimization algorithms (DEA-GNG, LMPFE, Subset Selection, NSGA3, SMS-EMOA, MOEA/D, MOEA/D-AWA, and UMOD) across various metrics, including Hypervolume (HV), Inverted Generational Distance (IGD), Spacing, Sparsity, Uniformity, Soft Uniformity, and Fill Distance. The full results for these biobjective problems can be found in Table 7. The numbers in parentheses represent standard deviations.

This table presents the performance of different multi-objective optimization methods on two fairness classification problems: Adult and Compass. The methods are compared across several metrics: Hypervolume (HV), Spacing, Sparsity, Uniformity, Soft Uniformity, and Fill Distance. The table shows the mean, standard deviation, and rank of each metric across five random seeds for each method.
This table shows a comparison of different multi-objective optimization algorithms on several biobjective problems. The metrics used for comparison include Hypervolume (HV), Inverted Generational Distance (IGD), Spacing, Sparsity, Uniformity, Soft Uniformity, and Fill Distance. The results shown are partial, with the complete results available in Table 7 of the paper. The table highlights the performance of UMOD in comparison to other state-of-the-art algorithms.

This table provides details about the datasets used in the fairness classification experiments, including the number of features, the architecture of the neural network used for classification, the activation function employed, the number of parameters in the network, the number of samples in each dataset, and the sensitivity attribute considered (sex).
This table lists the hyperparameters used in the UMOD-MOEA algorithm. It includes parameters for crossover, mutation, PFL (Pareto Front Learning) network training, preference initialization, and MOEA/D (Multi-Objective Evolutionary Algorithm based on Decomposition). The values chosen for these parameters are specified. The table is divided into two sections, one for crossover and PFL network parameters and another for mutation and MOEA/D parameters.

This table shows partial results for biobjective problems, comparing several multi-objective optimization algorithms including DEA-GNG, LMPFE, Subset selection, NSGA3, SMS-EMOA, MOEA/D, MOEA/D-AWA and UMOD. The algorithms are evaluated using several metrics such as Hypervolume (HV), Inverted Generalized Distance (IGD), Spacing, Sparsity, Uniformity, Soft Uniformity, and Fill Distance. The full results for these biobjective problems can be found in Table 7.

This table presents the results of seven different multi-objective optimization algorithms on several biobjective problems. The metrics used to evaluate the performance include hypervolume (HV), inverted generational distance (IGD), spacing, sparsity, uniformity, soft uniformity, and fill distance. The results are shown as mean and standard deviation for each metric, with rankings across all methods also provided. The last row shows the average ranking for each metric across all problems.

This table shows partial results for biobjective problems from the experiments. It compares seven different multi-objective optimization algorithms (DEA-GNG, LMPFE, Subset Selection, NSGA3, SMS-EMOA, MOEA/D, and MOEA/D-AWA) against the proposed UMOD method. The evaluation metrics used include Hypervolume (HV), Inverted Generational Distance (IGD), Spacing, Sparsity, Uniformity, Soft Uniformity, and Fill Distance. The results shown are partial, with complete results available in Table 7.
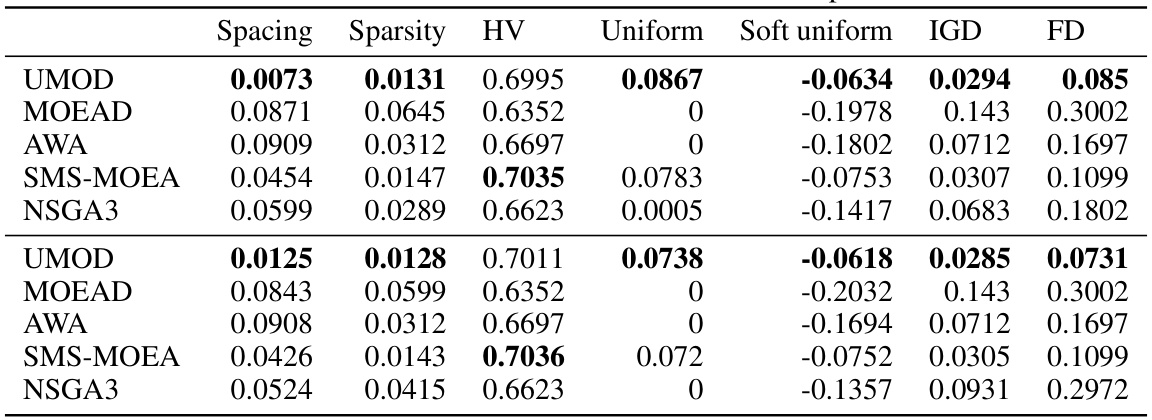
This table presents the numerical results for the DTLZ5 and DTLZ6 problems. It compares the performance of several multi-objective optimization algorithms (UMOD, MOEAD, AWA, SMS-MOEA, and NSGA3) across various metrics, including Spacing, Sparsity, Hypervolume (HV), Uniformity, Soft Uniformity, Inverted Generational Distance (IGD), and Fill Distance (FD). These metrics assess different aspects of algorithm performance, such as the uniformity and distribution of the obtained solutions on the Pareto front. The results show that UMOD generally outperforms other methods, particularly in achieving evenly distributed solutions.
Full paper#