↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Machine learning models often lack reliable uncertainty estimates, particularly in high-stakes applications like medical imaging and weather forecasting. Existing methods, such as deep ensembles, offer good uncertainty estimates, but they are computationally expensive to train, hindering their use with complex models. Single-model approaches offer a computationally cheaper alternative, but often have lower accuracy. This creates a need for methods that offer both accuracy and scalability.
This paper proposes HyperDM, a novel single-model approach to address these challenges. HyperDM uses conditional diffusion models and Bayesian hyper-networks to generate an ensemble of predictions. The results demonstrate that HyperDM provides uncertainty estimates comparable to or better than existing multi-model approaches, while significantly reducing computational costs. The method is validated on real-world tasks (CT reconstruction and weather forecasting), showcasing its ability to scale to modern network architectures.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on uncertainty quantification in machine learning, especially in high-stakes applications. It introduces a novel single-model approach that efficiently estimates both epistemic and aleatoric uncertainties, overcoming limitations of existing multi-model methods which are computationally expensive to train and scale poorly to complex models. This work opens new avenues for research in uncertainty quantification and enhances the reliability of ML models in critical domains like medical imaging and weather forecasting.
Visual Insights#
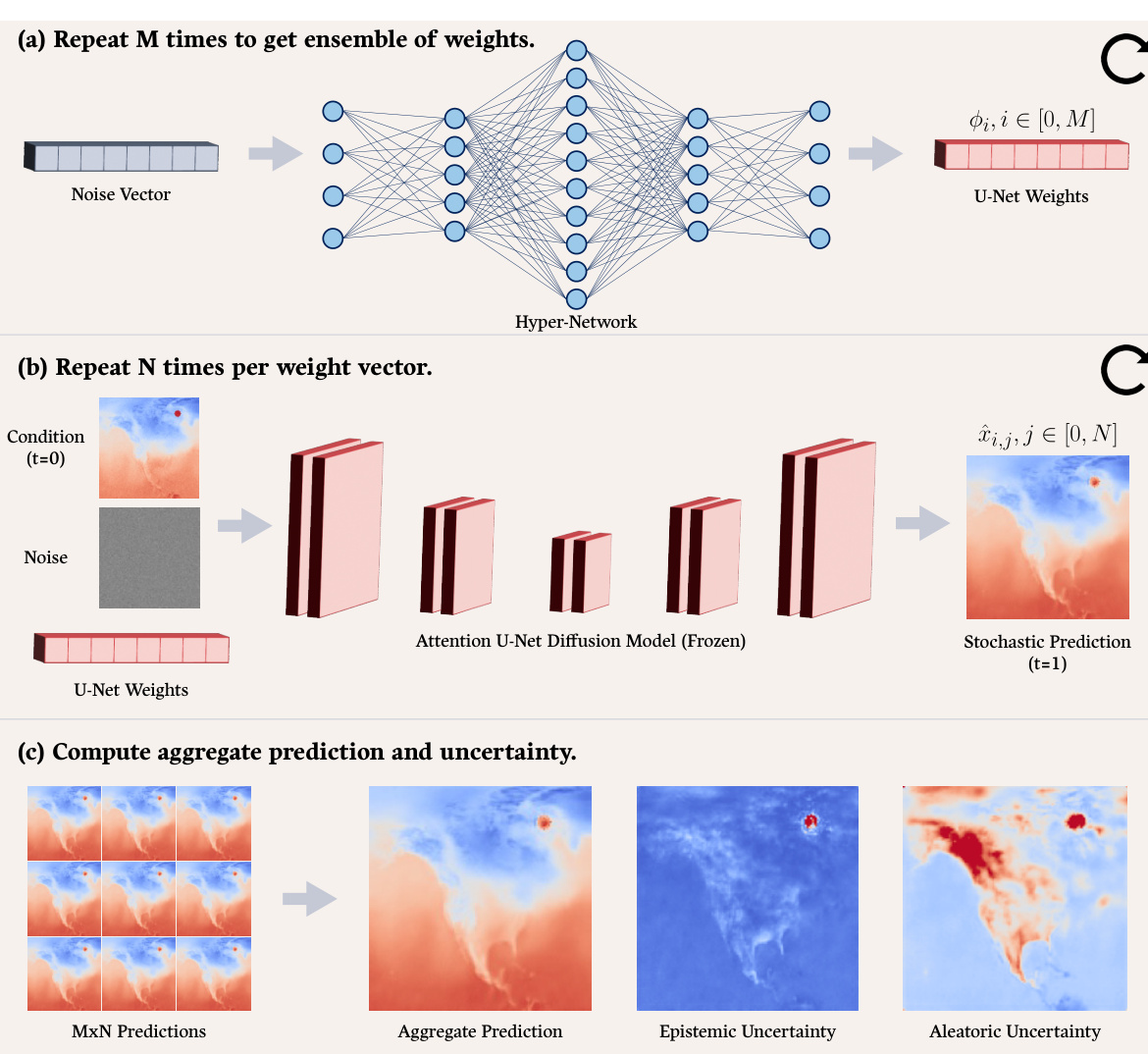
This figure illustrates the HyperDM framework. A Bayesian hypernetwork generates an ensemble of weights (a). Each weight set is used by a diffusion model to produce multiple predictions (b). Finally, these predictions are aggregated to get the final prediction and uncertainty maps which are separated into epistemic and aleatoric components (c).

This table compares the training and inference times for three different uncertainty quantification methods: MC-Dropout, DPS-UQ, and the proposed HyperDM method. It shows the time taken to train a 10-model ensemble (M=10) on the LUNA16 dataset and the time needed to generate a predictive distribution (M x N = 1000 samples) for a single input. The results highlight the computational efficiency of HyperDM compared to other methods.
In-depth insights#
HyperDM Framework#
The HyperDM framework presents a novel approach to estimating both epistemic and aleatoric uncertainty using a single model. This contrasts with traditional methods requiring multiple models, significantly reducing computational costs. The core innovation lies in combining a Bayesian hyper-network with a conditional diffusion model. The hyper-network generates an ensemble of diffusion model weights from random noise, enabling efficient sampling of diverse predictive distributions. This ensemble, processed through the conditional diffusion model, produces many predictions. These predictions are then aggregated to yield a final prediction and a decomposition of uncertainty into its epistemic and aleatoric components. This approach offers several advantages including scalability to modern network architectures, accuracy comparable to or exceeding ensemble methods, and improved uncertainty estimation. HyperDM’s ability to differentiate between these uncertainty types provides valuable insights for high-stakes applications like medical imaging and weather forecasting where reliable uncertainty quantification is crucial.
Uncertainty Estimation#
The core concept of the research paper revolves around uncertainty estimation, a critical aspect of machine learning, especially when dealing with high-stakes applications like medical imaging and weather forecasting. The authors address the challenge of disentangling epistemic uncertainty (reducible with more data) and aleatoric uncertainty (inherent to the task). Instead of relying on computationally expensive ensemble methods, they propose a novel single-model approach called HyperDM, which integrates a Bayesian hyper-network and a conditional diffusion model. This innovative approach allows for efficient estimation of both uncertainty types by generating an ensemble of predictions from a single model, thereby mitigating the computational burden of traditional ensembling techniques while maintaining prediction accuracy. HyperDM’s effectiveness is demonstrated through experiments on real-world datasets, showing superior performance compared to existing single-model methods and competitive results against multi-model ensembles.
Real-world Results#
A compelling ‘Real-world Results’ section would thoroughly showcase the efficacy of the proposed HyperDM model on practical, high-stakes applications. It should present results from multiple diverse domains, such as medical image reconstruction and weather forecasting, comparing HyperDM’s performance against established baselines like MC-Dropout and DPS-UQ. Key metrics for evaluation must include not only prediction accuracy (e.g., PSNR, SSIM) but also uncertainty quantification metrics (e.g., CRPS) to highlight HyperDM’s superior aleatoric and epistemic uncertainty estimation capabilities. Specific examples of out-of-distribution (OOD) scenarios and their handling by HyperDM would demonstrate its robustness. A quantitative analysis demonstrating reduced computational costs compared to ensemble methods is crucial. Visualizations of uncertainty maps, potentially showcasing the model’s ability to detect anomalies, would greatly enhance the section’s impact. The discussion should carefully analyze any limitations encountered in real-world applications, fostering trust in the model’s reliability and practicality.
Ablation Experiments#
Ablation experiments systematically remove components of a model or system to assess their individual contributions. In this context, they would likely involve removing or altering aspects of the HyperDM framework, such as the Bayesian hypernetwork, the diffusion model, or the ensemble prediction aggregation method. Analyzing the impact of these changes would reveal the importance of each part and provide insights into the model’s functionality. For instance, removing the Bayesian hypernetwork would help evaluate the role of ensembling in uncertainty estimation, while altering the diffusion model could highlight its contribution to the quality of predictions. By comparing performance metrics across different ablation configurations, such as uncertainty quantification accuracy, computational cost, and prediction accuracy, researchers could identify critical components and potential areas for improvement. Moreover, ablation studies might explore different hyperparameter settings within HyperDM. This would help understand how sensitive the system is to those parameters and to identify optimal configurations for improved performance. A thoughtful ablation study provides a deeper understanding of the model’s strengths, limitations, and the interplay of its components, which enhances the reliability of its uncertainty estimates.
Future Work#
The authors acknowledge the limitations of their approach and suggest several avenues for future research. Improving the speed of inference is crucial, as diffusion models are currently slower than conventional neural networks. This could involve exploring more efficient sampling strategies or adopting different generative models altogether. Addressing the scalability limitations of hypernetworks is another key area, as the number of hypernetwork parameters scales with the primary network’s size. Research into more efficient weight generation techniques or alternative architectural designs could mitigate this issue. Further investigation into the impact of sampling rates (number of weights and predictions per weight) is also warranted. While the paper shows the importance of sufficient sampling, a more detailed analysis of this trade-off, potentially involving theoretical frameworks, could provide deeper insights. Finally, expanding the evaluation to more complex and realistic scenarios is necessary. Though the paper validates its approach on two real-world tasks, testing on more datasets and considering additional performance metrics, such as robustness under different noise levels and data distributions, would strengthen its findings and demonstrate its generalizability.
More visual insights#
More on figures

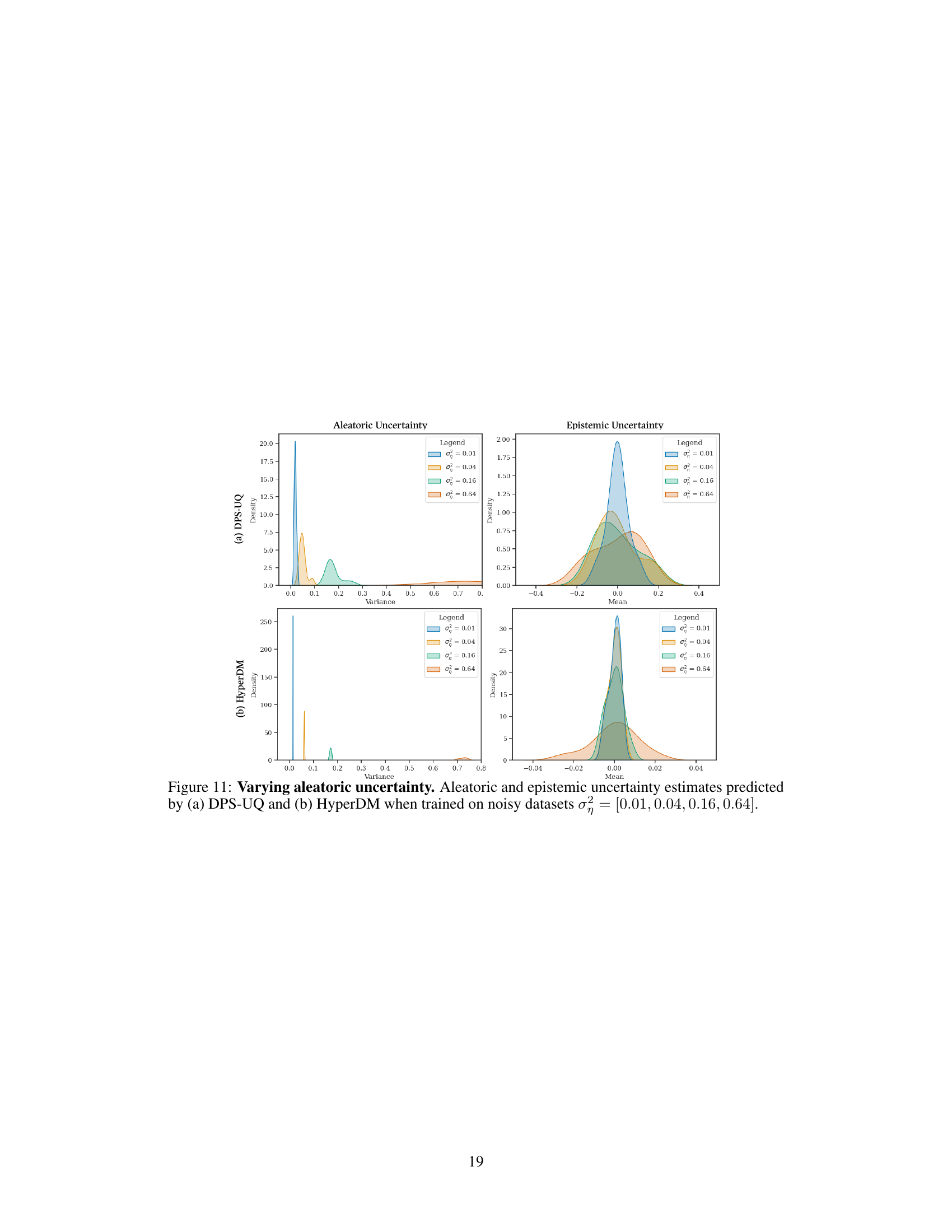
This figure shows the results of an experiment to validate the accuracy of HyperDM in estimating aleatoric and epistemic uncertainty. Two subfigures are shown. (a) demonstrates HyperDM’s ability to estimate aleatoric uncertainty by training on datasets with varying levels of inherent noise. The mean of the variance distribution for each dataset closely matches the true noise variance. (b) demonstrates HyperDM’s ability to estimate epistemic uncertainty by training on datasets with different sizes. The variance of the mean distribution for each dataset decreases inversely with dataset size, indicating accurate estimation of the uncertainty reduction with more data.

This figure shows a comparison of epistemic and aleatoric uncertainty maps generated by four different methods (MC-Dropout, DPS-UQ, and HyperDM) for a weather forecasting task. An out-of-distribution measurement was created by adding a synthetic ‘hot spot’ to a weather map. The figure demonstrates that HyperDM is superior at isolating the anomalous area within the epistemic uncertainty map compared to the other methods. It highlights the ability of HyperDM to accurately pinpoint areas where model uncertainty is high due to unusual data, which is a key advantage in high-stakes applications like weather forecasting.

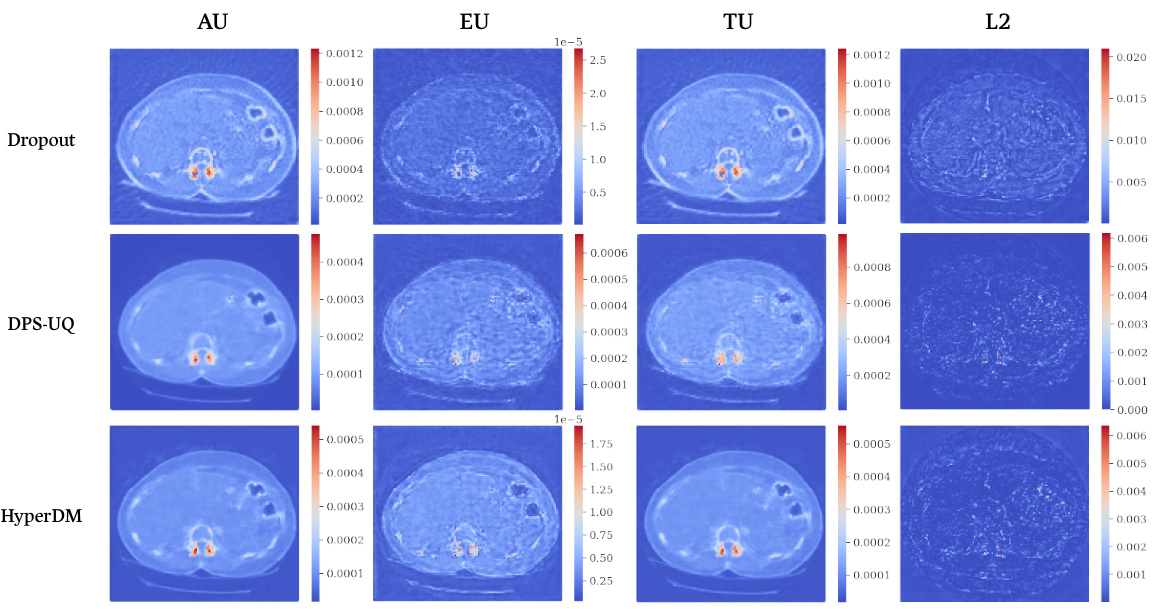
This figure shows the results of applying different uncertainty quantification methods to an out-of-distribution CT scan. The out-of-distribution scan contains synthetically added metal implants. The figure compares the performance of MC-Dropout, DPS-UQ, and HyperDM in detecting the anomaly, focusing on both epistemic (reducible with more data) and aleatoric (irreducible) uncertainty. The results highlight HyperDM’s ability to accurately identify the abnormal implants within its epistemic uncertainty map.

This figure shows a comparison of different uncertainty quantification methods on a weather forecasting task, where an out-of-distribution data point (a hot spot in northeastern Canada) is introduced. The subfigures (a) and (b) display the anomalous measurement and the uncertainty maps generated by various methods (MC-Dropout, DPS-UQ, and HyperDM), respectively. The uncertainty maps illustrate the epistemic (EU) and aleatoric (AU) uncertainty components. HyperDM demonstrates better performance at isolating the abnormal feature in the epistemic uncertainty estimate compared to other methods.

This figure shows the results of an ablation study on the HyperDM model, specifically investigating the impact of varying the number of sampled weights (M) on epistemic uncertainty estimation. Four images are presented, each corresponding to a different value of M (2, 4, 8, and 16). The images show uncertainty maps, where redder areas indicate higher uncertainty. As M increases, the uncertainty around an out-of-distribution feature (a hot spot in the upper-right quadrant) increases while uncertainty in other areas decreases, demonstrating that larger ensemble sizes improve the identification of anomalies.

This figure shows the effect of increasing the number of predictions (N) sampled from the diffusion model on the aleatoric uncertainty estimates. As N increases from 2 to 16, the uncertainty maps become smoother and less noisy, indicating a more stable and reliable representation of the inherent randomness in the predictions.
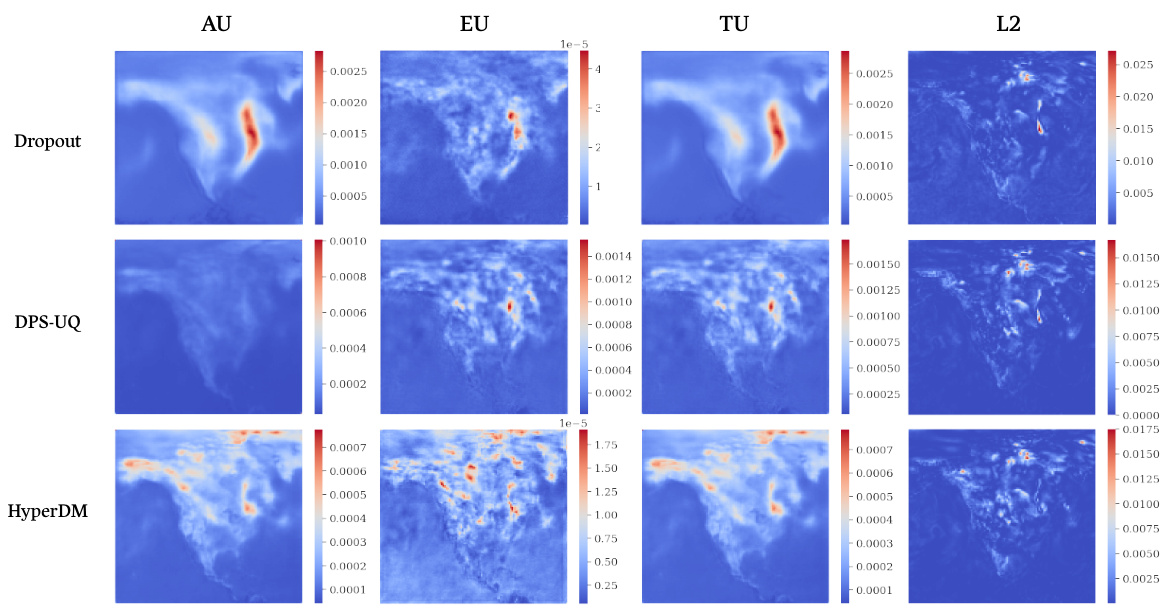
This figure shows the results of weather forecasting experiments using four different methods (MC-Dropout, DPS-UQ, and HyperDM) on out-of-distribution data. The out-of-distribution data was created by adding a ‘hot spot’ to a weather map in northeastern Canada. The figure shows the epistemic and aleatoric uncertainty maps for each method, highlighting how well each method can identify and isolate the abnormal feature (the hot spot). HyperDM shows the best results at isolating the abnormal feature in its epistemic estimate.
This figure compares the performance of different uncertainty quantification methods (MC-Dropout, DPS-UQ, and HyperDM) on a weather forecasting task when an out-of-distribution measurement (a synthetically added hot spot in northeastern Canada) is introduced. The figure shows the epistemic and aleatoric uncertainty maps generated by each method. HyperDM demonstrates superior performance in isolating the anomalous feature, highlighting its effectiveness in identifying unexpected events or data anomalies in real-world prediction tasks.

This figure demonstrates the accuracy of HyperDM in estimating both aleatoric and epistemic uncertainty. In (a), four datasets with varying aleatoric uncertainty (controlled by noise variance) are used to train HyperDM, and the resulting variance of predictions accurately reflects the input noise. In (b), four datasets of varying sizes are used, demonstrating that HyperDM accurately estimates epistemic uncertainty (which decreases as dataset size increases).
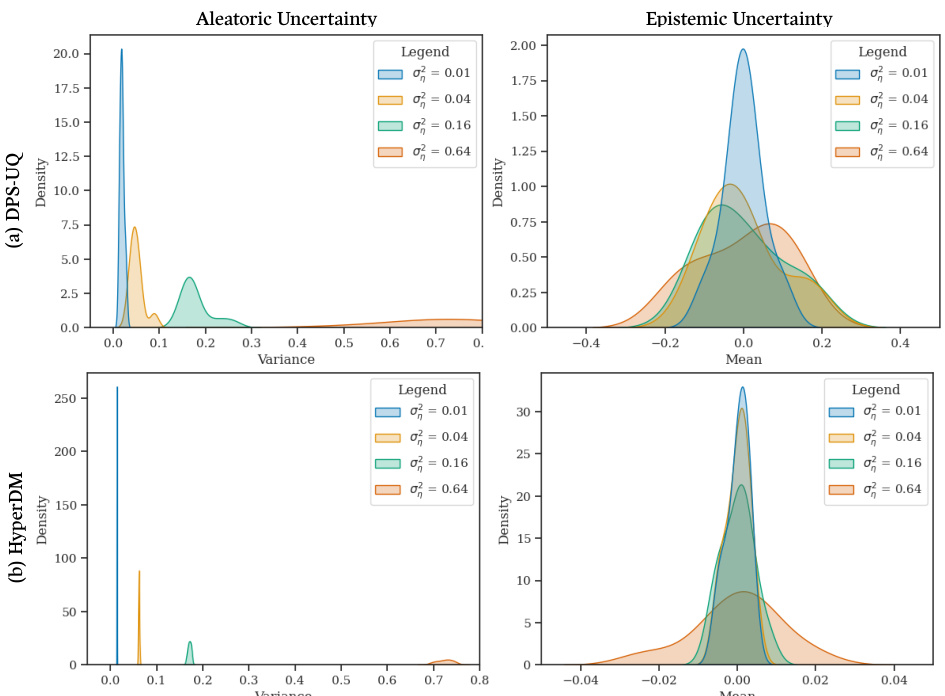
This figure shows the results of an experiment to validate HyperDM’s ability to estimate aleatoric and epistemic uncertainty. Panel (a) demonstrates the accurate estimation of aleatoric uncertainty (inherent noise in the data) by showing that the mean variance of predictions from the model matches the true variance in the data. Panel (b) demonstrates the accurate estimation of epistemic uncertainty (uncertainty due to limited data) by showing that the variance of the prediction means decreases as the amount of training data increases.
More on tables

This table compares the performance of three different methods (MC-Dropout, DPS-UQ, and HyperDM) for estimating uncertainty in two real-world tasks: CT reconstruction and weather forecasting. The metrics used are SSIM, PSNR, and CRPS. Higher SSIM and PSNR values indicate better image quality, while a lower CRPS value indicates better uncertainty estimation. The best and second-best results for each method and dataset are highlighted in red and blue, respectively.

This table compares the performance of three different methods (MC-Dropout, DPS-UQ, and HyperDM) for estimating uncertainty in two real-world applications: Computed Tomography (CT) image reconstruction (LUNA16 dataset) and weather forecasting (ERA5 dataset). For each dataset and method, it reports the Structural Similarity Index (SSIM), Peak Signal-to-Noise Ratio (PSNR), L1 error, and Continuous Ranked Probability Score (CRPS). Higher SSIM and PSNR values indicate better image quality, while lower L1 and CRPS values indicate better prediction accuracy and uncertainty estimation, respectively. The best and second-best results for each metric are highlighted in red and blue, respectively.

This table compares the performance of three different methods (MC-Dropout, DPS-UQ, and HyperDM) for estimating uncertainty in real-world datasets. The metrics used are SSIM, PSNR (dB), and CRPS. The results show that HyperDM generally achieves higher image quality and lower uncertainty scores compared to the baselines. The use of two datasets, LUNA16 (CT scans) and ERA5 (weather forecasting), helps demonstrate the robustness and generalizability of the proposed HyperDM.
Full paper#