↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Current diffusion-based inverse problem solvers frame signal recovery as probabilistic sampling, encountering issues such as intractable likelihood functions, strict score network reliance, and poor initial guess prediction. These methods often suffer from sensitivity to discretization and approximation errors, hindering their accuracy and robustness.
This research proposes an innovative solution by transforming the generative process into a discrete optimal control problem. A diffusion-based optimal controller, inspired by iterative Linear Quadratic Regulator (iLQR), is developed, capable of handling diverse forward operators (super-resolution, inpainting, etc.). The resulting algorithm is shown to overcome prior limitations by accurately recovering the idealized posterior sampling equation. The method demonstrates significant improvement in solving various inverse problems, achieving state-of-the-art image reconstruction results.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on inverse problems, diffusion models, and optimal control. It offers a novel framework that significantly improves the performance and robustness of existing methods. This opens new avenues for research into more efficient and accurate solutions for various inverse problems across many domains. The combination of these techniques provides a state-of-the-art benchmark for image reconstruction.
Visual Insights#
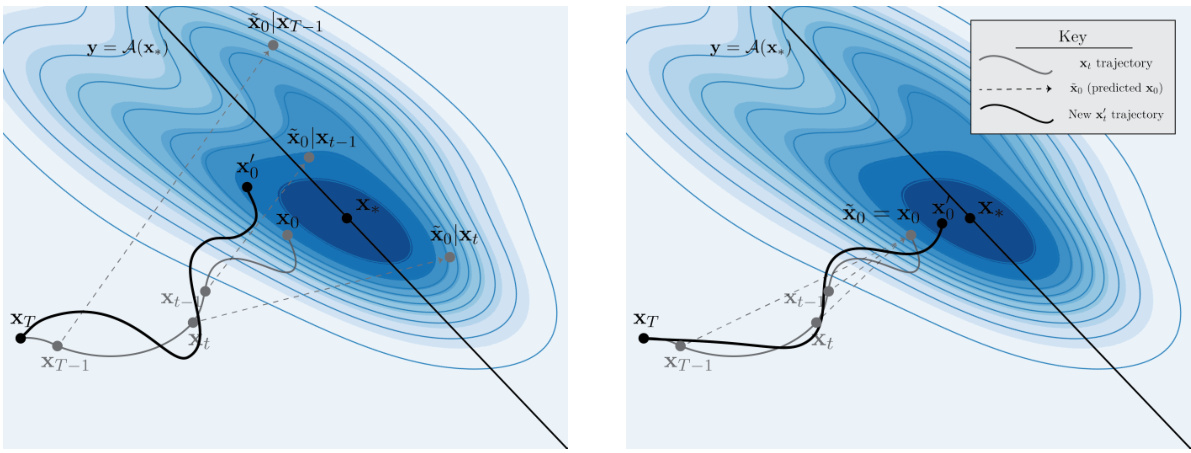
This figure compares two different approaches to solving inverse problems using diffusion models. The left side shows a probabilistic posterior sampler which estimates the initial state (x0) and uses this approximation to guide the sampling process. The right side illustrates the proposed optimal control-based sampler, where the initial state is calculated exactly at each step, providing higher quality gradients and a more accurate trajectory update. This results in better accuracy and stability across different number of steps.

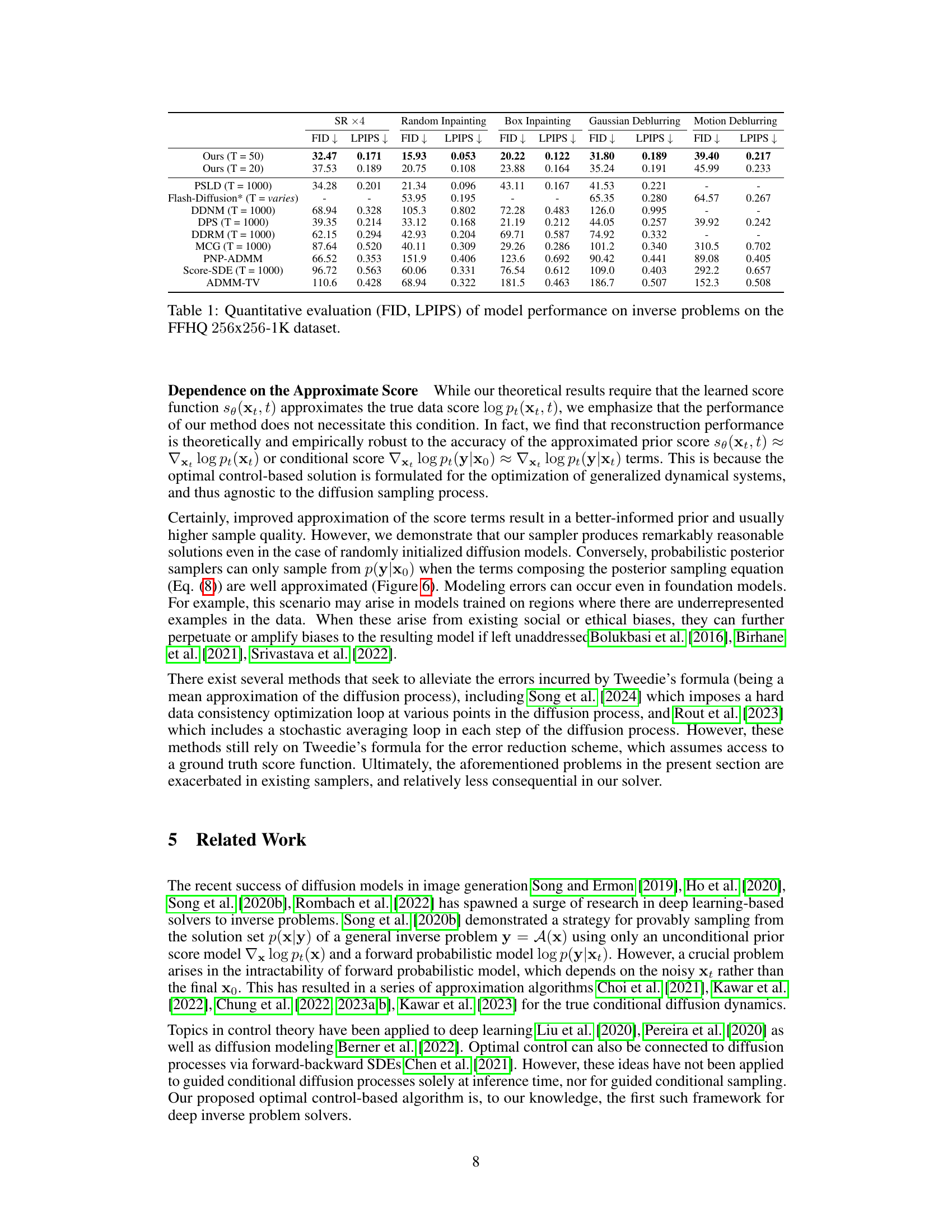
This table presents a quantitative comparison of different methods for solving various inverse problems on the FFHQ 256x256-1K dataset. The performance is measured using two metrics: Fréchet Inception Distance (FID) and Learned Perceptual Image Patch Similarity (LPIPS). Lower values indicate better performance for both metrics. The table includes results for various methods, including different variants of the proposed Diffusion Optimal Control method, as well as several baselines like Diffusion Posterior Sampling (DPS) and Plug-and-Play ADMM (PNP-ADMM). The results are broken down by inverse problem type (super-resolution, inpainting, deblurring).
In-depth insights#
Diffusion Optimal Ctrl#
The heading ‘Diffusion Optimal Control’ suggests a novel approach to solving inverse problems. It cleverly combines the strengths of diffusion models, known for their generative capabilities, with optimal control theory, a powerful framework for guiding dynamic systems. This approach likely addresses limitations of existing diffusion-based inverse problem solvers by framing the generative process as a discrete optimal control problem. This reframing allows for more precise control over the sampling process, potentially leading to improved reconstruction quality and robustness to noise. The use of optimal control theory likely enables the method to handle a broader range of inverse problems by directly optimizing the system’s trajectory toward the desired solution, rather than relying solely on score function approximations. This direct optimization could mitigate issues like poor initial prediction quality, a common weakness of probabilistic sampling methods. The algorithm’s generality, as suggested by the heading, might mean it’s applicable to diverse tasks such as super-resolution, inpainting, and deblurring. Overall, ‘Diffusion Optimal Control’ points towards a powerful, potentially state-of-the-art, method for inverse problems leveraging the best aspects of both generative modeling and control theory.
Posterior Sampling#
Posterior sampling, in the context of diffusion models for inverse problems, aims to generate samples from a target posterior distribution representing the desired solution given observed data. The core challenge lies in the intractability of the conditional likelihood function, making direct sampling infeasible. Existing methods often resort to approximating the conditional score function, which introduces significant errors and limits accuracy. The paper proposes an alternative perspective, shifting away from direct posterior sampling to an optimal control framework. This approach leverages the iterative nature of diffusion processes, framing the inverse problem as a discrete optimal control episode. By formulating a cost function that reflects the distance from the desired solution, the method elegantly avoids explicit calculation of the often-intractable conditional likelihood. Instead, it directly learns an optimal control strategy to guide the diffusion process towards the desired posterior, resulting in significant performance improvements. This strategy makes the method robust to the accuracy of score network approximations, overcoming a key limitation of conventional probabilistic approaches. Ultimately, this novel approach offers a more accurate, robust, and efficient method for solving inverse problems using diffusion models.
High-Dim Control#
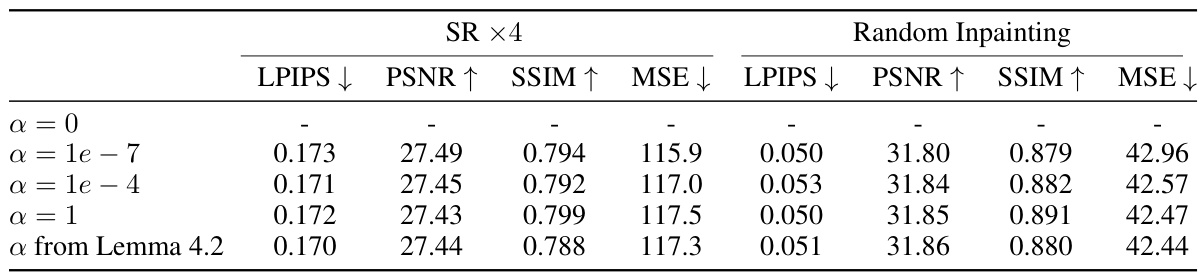
The section on ‘High-Dim Control’ in this research paper tackles the significant computational challenges associated with applying optimal control methods, specifically the iterative Linear Quadratic Regulator (iLQR), to high-dimensional systems. This is a critical issue because many real-world problems, such as image processing and reconstruction (the focus of this paper), naturally involve high-dimensional data. The core problem is the sheer size of the matrices involved in calculating gradients and Hessians, leading to memory constraints and prohibitive computational costs. The paper addresses this by introducing three key innovations: First, it leverages randomized low-rank matrix approximations, significantly reducing memory requirements and computational complexity. Second, a matrix-free approach is used, avoiding explicit matrix formation to further reduce costs. Finally, an adaptive Adam optimizer replaces the typical backtracking line search, accelerating convergence. These strategies are crucial for making optimal control applicable to realistically sized inverse problems. The analysis highlights the trade-offs inherent in these choices; for example, low-rank approximations introduce approximation error, and the choice of optimizer influences performance. The overall impact of these techniques is a significant improvement in efficiency, making it feasible to apply optimal control to high-dimensional problems that were previously intractable, therefore extending its applicability to complex scenarios and real-world datasets.
Inverse Problem#
Inverse problems, where the goal is to infer an unobserved cause from its observed effect, are a central theme in many scientific fields. The challenge lies in the ill-posed nature of these problems, often involving non-unique solutions or extreme sensitivity to noise. Diffusion models offer a powerful probabilistic approach, framing the inverse problem as sampling from the posterior distribution of the unknown signal given noisy measurements. However, traditional diffusion-based methods often encounter limitations such as the difficulty in accurately approximating the conditional score function and the computational burden of high-dimensional inference. The proposed diffusion optimal control approach addresses these issues by reframing the inverse problem as a discrete optimal control episode, enabling efficient and stable solutions. By leveraging the iterative Linear Quadratic Regulator (iLQR) algorithm, this method sidesteps the need for computationally expensive score function approximation and allows for flexible handling of complex forward operators. The theoretical foundation of this approach is rooted in optimal control theory, providing a rigorous framework for analyzing and solving inverse problems. Empirical results showcase significant improvements in image reconstruction tasks, demonstrating the efficacy and robustness of this novel methodology.
Future Work#
Future research directions stemming from this work on diffusion optimal control for inverse problems could explore several promising avenues. Extending the framework to handle more complex forward models beyond those considered in the paper (e.g., involving non-differentiable or stochastic components) is a key area. Investigating alternative control strategies beyond iLQR, such as model predictive control or reinforcement learning approaches, could potentially improve efficiency or robustness. Analyzing the theoretical properties of the method under less restrictive assumptions (e.g., weaker noise models or approximations of the score function) could further enhance its understanding and general applicability. Incorporating learned priors into the optimization could help improve the quality of reconstructions. Finally, applying the method to diverse real-world applications in areas like medical imaging, remote sensing, and materials science, could showcase its practical benefits and drive further refinement.
More visual insights#
More on figures

This figure compares the predicted x0 (initial state of the reverse diffusion process) in a probabilistic framework versus the proposed optimal control framework. The probabilistic framework uses an approximation of x0, whereas the proposed framework computes x0 exactly using a full forward rollout. This leads to more efficient computation of the gradient of the log-likelihood and improved trajectory updates in the optimal control method.

This figure compares the performance of the proposed diffusion optimal control method against the Diffusion Posterior Sampling (DPS) method for a 4x super-resolution task. It shows the reconstructed images at different numbers of diffusion timesteps (T). The top row shows the results from DPS, while the bottom row displays the results from the proposed method. The figure demonstrates that the proposed method generates higher-quality images that better adhere to the constraint Ax = y (where A is the forward operator and y is the measured signal), and exhibits greater stability across various T values. The improvements highlight the method’s robustness and effectiveness in solving inverse problems.

This figure showcases the results of four different inverse problem solving methods on the FFHQ 256x256 dataset. The four methods compared are: ground truth, measurement (the corrupted input), Diffusion Posterior Sampling (DPS), and the authors’ proposed method. The figure demonstrates the relative success of each method at reconstructing the original image from a degraded version. The image examples are split into two categories: Super Resolution 4x and Random Inpainting.

This figure compares the performance of the proposed Diffusion Optimal Control method against the Diffusion Posterior Sampling (DPS) method on a class-conditional inverse problem using the MNIST dataset. Each row in the figure shows the results for a different MNIST digit class (0-9). The left column displays samples generated by DPS, while the right column shows samples generated by the proposed method. The goal is to reconstruct a MNIST digit given only its class label. The figure demonstrates that the proposed method achieves better visual results than DPS in terms of digit clarity and overall quality, suggesting superior performance.

This figure compares the performance of the proposed diffusion optimal control method to Diffusion Posterior Sampling (DPS) on a 4x super-resolution task. It shows that the proposed method generates higher-quality results that are more consistent across different numbers of diffusion timesteps (T), better adhering to the constraint Ax = y (where A is the forward operator, x is the unknown signal, and y is the measurement). The top row depicts results from DPS, while the bottom row shows the results from the proposed method.
More on tables

This table lists the hyperparameters used for the FFHQ experiments in the paper. It specifies the total diffusion steps (T), the number of iterations (num_iters), the step size, the terminal cost function (lo(x0)), the Tikhonov regularization parameter (α), the running cost function (lt(xt, ut)), the rank (k) of low-rank approximations, and the control mode (input or output perturbation). The values are specific to each of the five inverse problems considered: super-resolution (SR × 4), random inpainting, box inpainting, Gaussian deblurring, and motion deblurring. This level of detail is important for reproducibility.

This table presents a quantitative comparison of different methods for solving various inverse problems on the FFHQ 256x256-1K dataset. The methods are evaluated using two metrics: FID (Fréchet Inception Distance) and LPIPS (Learned Perceptual Image Patch Similarity). Lower FID and LPIPS scores indicate better performance. The table shows that the proposed ‘Ours’ method achieves state-of-the-art performance across all five inverse problems (super-resolution, random inpainting, box inpainting, Gaussian deblurring, and motion deblurring).
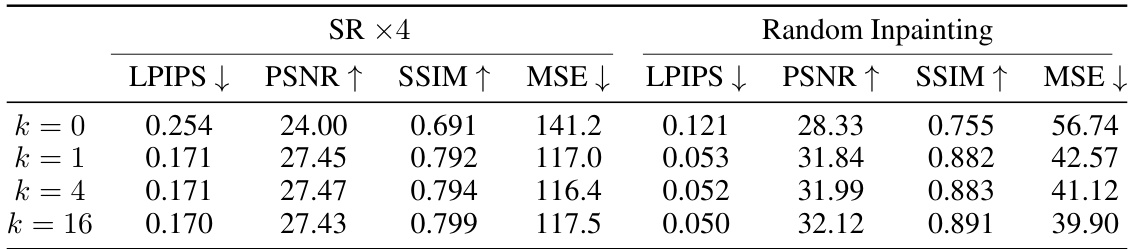
This table presents the results of an ablation study on the impact of rank in low-rank and matrix-free approximations within the proposed diffusion optimal control method. It shows how the performance metrics (LPIPS, PSNR, SSIM, and NMSE) vary as the rank (k) is changed from 0 to 16 on the FFHQ 256x256-1K dataset for super-resolution and random inpainting tasks. The study aims to demonstrate the impact of the approximation technique on the model’s efficiency and effectiveness.
This table presents the results of an ablation study conducted to evaluate the impact of rank in low-rank approximations and matrix-free evaluations on the performance of the proposed model. The study uses the FFHQ 256x256-1K dataset and assesses performance using LPIPS, PSNR, SSIM, and NMSE metrics. Different ranks (k=0, 1, 4, 16) are tested for the low-rank approximation, while matrix-free evaluation is also investigated. The table helps understand the effect of model complexity on its performance.
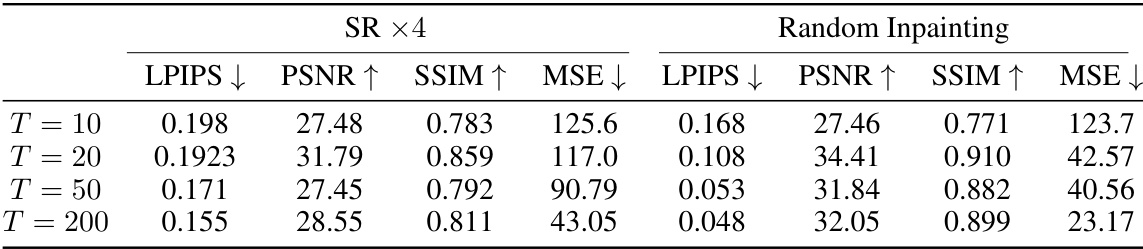
This table shows the results of an ablation study on the effect of the total number of diffusion timesteps (T) on the performance of the proposed model. The performance metrics used are LPIPS, PSNR, SSIM, and NMSE. The results are shown for two different inverse problems: 4x super-resolution and random inpainting. The results demonstrate that increasing the number of timesteps leads to improved performance, but with diminishing returns.
Full paper#