↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world machine learning problems involve corrupted or misspecified data. Existing work often focuses on uniform corruption or misspecification bounds, failing to capture scenarios where the error scales with the action’s suboptimality. This limits the applicability of these methods.
This research introduces novel algorithms specifically designed for linear bandits with corrupted rewards. The key innovation is to consider two types of corruption: strong (corruption level depends on learner’s action) and weak (corruption is independent of action). The study fully characterizes the minimax regret for stochastic linear bandits under both corruptions and develops upper and lower bounds for adversarial settings. Importantly, it links corruption-robust algorithms to those that handle gap-dependent misspecification, achieving optimal results.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between corruption-robust learning and learning with gap-dependent misspecification. It provides a unified framework for analyzing these issues, offers efficient algorithms with optimal scaling in corruption levels, and extends these findings to reinforcement learning. This work is timely, given the increasing focus on robust learning in real-world applications.
Visual Insights#

Figure 1(a) shows the bonus function used in Algorithm 2, which adds an exploration bonus to compensate for the bias of the reward estimator in the presence of corruption. Figure 1(b) provides a geometric interpretation of the bonus function, illustrating how it adjusts the covariance matrix to account for corruption and ensure sufficient exploration. The bonus function ensures that the exploration bonus term is always positive semi-definite and is carefully designed to achieve optimal regret bounds.
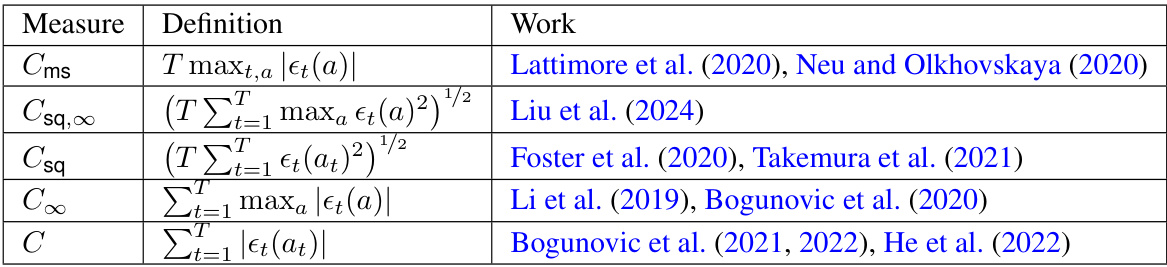
This table summarizes the upper and lower bounds on the regret for stochastic and adversarial linear bandits under two different corruption measures: C and C∞. The C measure represents strong corruption, where the corruption level depends on the learner’s action, while C∞ represents weak corruption, where it does not. The table highlights the gap between the minimax regret under these two types of corruptions, showing how the optimal scaling for the corruption level varies based on the bandit setting.
Full paper#



















