Query-Efficient Correlation Clustering with Noisy Oracle

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in query-efficient clustering and online learning, particularly those working with noisy data. It provides novel algorithms with theoretical guarantees, addressing a significant limitation in existing methods. The results open up new research avenues in combinatorial multi-armed bandits (CMAB) and NP-hard offline optimization problems.

Visual Insights

#

The figure shows the sample complexity of KC-FC and Uniform-FC for four different real-world graphs (Lesmis, Adjnoun, Football, Jazz). The x-axis represents the lower bound on the minimum gap (Amin) which is varied from 0.1 to 0.5. The y-axis shows the sample complexity (number of queries). As can be seen, the sample complexity of KC-FC is much smaller than that of Uniform-FC. The sample complexity of Uniform-FC makes the algorithm prohibitive even for small instances. As Amin increases, the sample complexity of KC-FC becomes smaller, a desirable property not possessed by Uniform-FC.

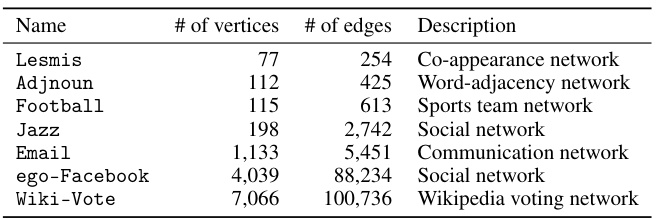
This table lists seven real-world graphs used in the paper’s experiments. For each graph, the number of vertices (nodes), the number of edges (connections between nodes), and a short description of what the graph represents are provided. These graphs represent diverse network structures, including social networks, word adjacency networks, and a sports team network, and are used to evaluate the performance of the proposed query-efficient correlation clustering algorithms.

In-depth insights

#

Noisy Oracle PE-CMAB

#

The concept of “Noisy Oracle PE-CMAB” blends the challenges of noisy data with the exploration-exploitation trade-off inherent in Pure Exploration Combinatorial Multi-Armed Bandits (PE-CMAB). A noisy oracle introduces uncertainty into the feedback received, making it difficult to accurately assess the value of different actions (arms). In a PE-CMAB setting, the goal is to efficiently identify the best combination of arms (often an NP-hard problem). The combination of these aspects makes the problem significantly more complex than standard PE-CMAB. Effective strategies must account for both noise and the combinatorial nature of the action space, potentially requiring sophisticated sampling techniques, adaptive querying algorithms, and theoretical guarantees under noisy conditions. This field would benefit from both theoretical advances (like tighter bounds on sample complexity and error probability) and practical algorithms that can handle noisy real-world applications.

KC-FC & KC-FB

#

The algorithms KC-FC and KC-FB, designed for query-efficient correlation clustering with noisy oracles, represent a novel approach to tackling this challenging problem. KC-FC, framed within a fixed confidence setting, prioritizes finding a high-quality solution with a guaranteed probability, while minimizing the number of queries. Conversely, KC-FB, operating under a fixed budget, aims to maximize the likelihood of obtaining a good solution given a limited number of queries. Both leverage a combination of sampling strategies informed by threshold bandits and the classic KwikCluster approximation algorithm. A key strength lies in their theoretical guarantees, providing upper bounds on the number of queries for KC-FC and demonstrating exponentially decreasing error probability with increasing budget for KC-FB. Crucially, these algorithms address the NP-hard nature of the underlying offline correlation clustering problem, making them unique in the field of polynomial-time PE-CMAB algorithms. Their empirical performance validates the theoretical findings, showcasing their effectiveness over baseline methods in both sample complexity and solution quality.

Approximation Bounds

#

Approximation bounds in the context of correlation clustering, especially when dealing with noisy oracles, are crucial for evaluating algorithm performance. They quantify the trade-off between computational efficiency and solution quality. A strong approximation bound guarantees that the algorithm’s output is within a certain factor of the optimal solution, even with noisy or incomplete data. The challenge lies in designing algorithms that maintain tight approximation bounds while minimizing the number of queries to a potentially noisy oracle. This involves carefully balancing exploration (learning the similarity measures) and exploitation (using the learned information for clustering). The development of polynomial-time algorithms with strong approximation bounds is a significant achievement, especially given the NP-hard nature of the underlying offline optimization problem. However, the approximation bounds usually have an additive error term, reflecting the inherent uncertainty introduced by noisy oracles. Future research should explore ways to tighten these bounds and investigate the impact of different noise models on the achievable approximation guarantees.

Query Efficiency

#

The concept of ‘Query Efficiency’ in this research paper centers on minimizing the number of queries to a noisy oracle needed to achieve a high-quality correlation clustering. The authors cleverly address the challenge of computationally expensive and inherently noisy similarity measures by framing the problem within the Pure Exploration setting of Combinatorial Multi-Armed Bandits (PE-CMAB). This novel approach allows them to develop algorithms that balance the exploration of similarities with the need for efficient clustering. Two distinct settings are explored: a fixed confidence setting that aims to achieve a target accuracy level with the fewest queries, and a fixed budget setting that maximizes accuracy given a limited query budget. Theoretical guarantees are provided showing that the proposed algorithms offer polynomial-time solutions that achieve near-optimal approximations to the true clustering solution, even with noisy data. The empirical results demonstrate the superior query efficiency of the developed algorithms compared to simpler, baseline approaches. The work makes significant contributions to the field by effectively tackling the NP-hard correlation clustering problem in a query-efficient manner, with theoretical guarantees that bridge the gap between theory and practice.

Future Work

#

The paper’s conclusion points towards several promising avenues for future research. Deriving information-theoretic lower bounds for pure exploration in combinatorial multi-armed bandits (PE-CMAB) problems with NP-hard offline optimization is highlighted as a significant challenge. This is crucial for understanding the fundamental limits of query-efficient algorithms in this setting. Additionally, exploring variations of correlation clustering and considering scenarios with heteroscedastic noise (where noise variance differs across data points) are suggested. Investigating alternative noisy oracle models, perhaps incorporating adversarial noise or more complex feedback mechanisms, could provide additional insights. Finally, the authors suggest exploring the application of their findings to other clustering tasks or related problems where noisy similarity information is prevalent. These directions are all important next steps to further advance the field of query-efficient correlation clustering.

More visual insights

#

More on figures

This figure compares the cost of clustering obtained by KC-FC (the proposed algorithm) and KwikCluster (a baseline algorithm that has access to the true similarity). The x-axis represents the lower bound on the minimum gap (Amin) and y-axis represents the cost of clustering. For each dataset (Lesmis, Adjnoun, Football, Jazz), it shows that KC-FC achieves comparable clustering quality to KwikCluster. This demonstrates that KC-FC is effective in estimating the underlying similarity, despite having access only to noisy feedback.

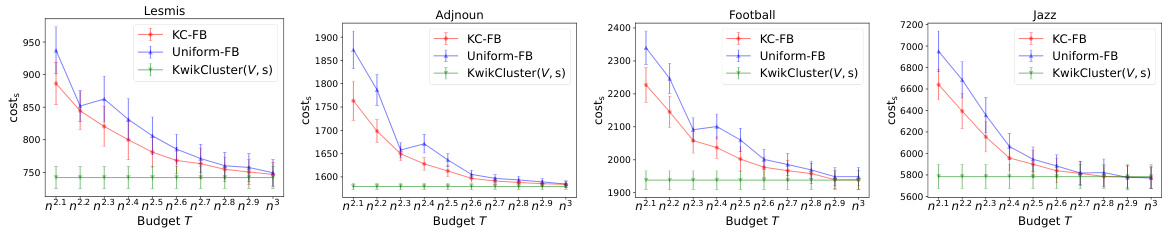
The figure shows the cost of clustering for four datasets (Lesmis, Adjnoun, Football, Jazz) with different sizes. The algorithms compared are KC-FB (the proposed algorithm), Uniform-FB (a baseline method), and KwikCluster (an optimal algorithm having access to true similarity). The x-axis represents the budget T (number of queries) that varies from n^2.1 to n³, and the y-axis is the cost of the clustering. The figure demonstrates that KC-FB consistently outperforms Uniform-FB in terms of clustering cost, showing the effectiveness of KC-FB’s adaptive sampling strategy. KwikCluster, which uses the true similarity, naturally performs the best, serving as an upper bound.

More on tables

This table presents the results of comparing the cost of clustering produced by three different algorithms: KC-FB, Uniform-FB, and KwikCluster (with full knowledge of similarity). The comparison is made for three real-world datasets (Email, ego-Facebook, Wiki-Vote) with a minimum of 1000 vertices each. For each algorithm and dataset, the average cost and standard deviation are reported. The table is designed to show how the cost of KC-FB compares with a naive sampling approach (Uniform-FB) and an ideal scenario where the similarity is fully known (KwikCluster).

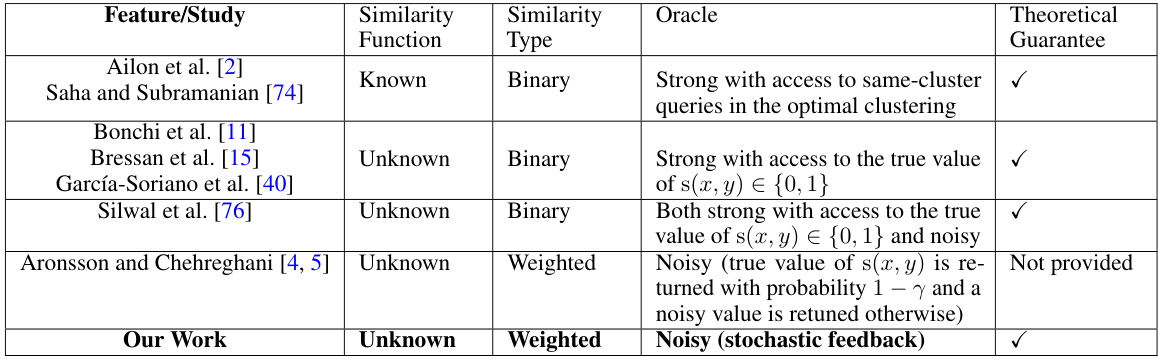
This table compares different approaches to query-efficient correlation clustering. It highlights key differences in the similarity function used (binary or weighted), the type of oracle used (strong or noisy), and whether the approach provides a theoretical guarantee on the quality of the results. The table is useful for understanding the novelty and contributions of the authors’ proposed method in the context of existing work.

Full paper

#