↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Large language models (LLMs) are powerful but slow. Speculative decoding accelerates inference by using a small, fast model to generate draft tokens, which a large, accurate model validates. However, a theoretical understanding of this approach was lacking. This paper addresses that gap. The paper starts by describing the challenges in LLM decoding that stem from the autoregressive nature of transformer models. The decoding process is significantly time-consuming as the model size scales up, which results from each generated token serving as input for future generations. This limitation has led to the development of techniques such as speculative decoding to mitigate this issue.
This paper provides a theoretical analysis of speculative decoding using a Markov chain abstraction. It derives precise formulas for the expected number of rejections, which directly relates to inference time. The study proves that speculative decoding is optimal in a certain class of algorithms, establishing theoretical limits on acceleration. It also explores the trade-off between output quality and inference speed, offering a novel optimization model and revealing the fundamental relationships among LLM components. This theoretical analysis enhances our understanding of the mechanisms that govern the performance of speculative decoding, enabling a more data-driven and informed approach to designing and optimizing efficient decoding algorithms.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large language model (LLM) inference acceleration because it provides a much-needed theoretical foundation for speculative decoding, a promising technique to speed up LLMs. The analysis of theoretical limits, tradeoffs, and optimality offers valuable insights into the design of efficient decoding algorithms. It also opens up new research directions in optimizing speculative decoding for improved quality and efficiency.
Visual Insights#

This figure compares the standard autoregressive decoding method with the proposed speculative decoding method. In the standard method (left), the large language model (LLM) generates tokens one by one in an autoregressive manner. In the speculative decoding method (right), a smaller, faster draft model generates a sequence of tokens, which are then validated by the LLM. If a token is rejected by the LLM, the draft model generates a new sequence from the last accepted token. This process speeds up inference, as the smaller model is much faster than the LLM.

This table presents the results of a simple experiment comparing two decoding methods: Decoding-OPT (using the optimal distribution from Theorem 4) and Decoding-UNO (using the target distribution as a suboptimal solution). The experiment uses pythia-70m as the draft model and pythia-2.8b as the target model. The WinRate is used as the metric for quality, indicating the percentage of prompts where Decoding-OPT outperforms Decoding-UNO. Different over-acceptance thresholds (epsilon values) are tested using two different score models: RM-Mistral-7B and GPT-4. The results show that Decoding-OPT consistently outperforms Decoding-UNO across various epsilon values and score models.
In-depth insights#
SD Formalization#
A section titled ‘SD Formalization’ in a research paper would likely delve into the mathematical and computational framework for speculative decoding (SD). It would likely begin by defining SD precisely, perhaps contrasting it with traditional autoregressive decoding. The core of the section would focus on representing SD’s key components—the small draft model, the large validation model, the acceptance/rejection criterion—as mathematical objects. Markov chains and probability distributions are likely candidates for this formalization. The authors might then derive key properties of the formalized SD process, such as the expected number of rejections or the relationship between the distributions of the draft and validation models and the overall decoding speed. Theoretical bounds on SD performance, potentially under different assumptions on model capabilities, could also be presented. This rigorous formalization would provide a foundation for analyzing SD’s efficiency, optimality, and potential for improvement, moving beyond empirical observations to a deeper theoretical understanding. The use of total variation distance or similar metrics to quantify model discrepancies would also be expected. Ultimately, such a section would be crucial in providing a solid theoretical base for future advancements in speculative decoding algorithms.
SD Optimality#
The heading ‘SD Optimality’ likely refers to a section exploring the optimality of Speculative Decoding (SD) algorithms. A key aspect would be proving whether SD, in its core design, represents the best possible approach to balance speed and accuracy. The analysis may involve comparing SD’s performance against a broader class of rejection-based decoding methods, possibly demonstrating that no unbiased algorithm can achieve fewer rejections than SD. This would establish SD’s optimality within its defined constraints. The discussion might also consider the tradeoffs between optimality and practical considerations, such as the computational cost of the oracle (the large language model) calls and the need for parallel processing. It’s also likely that the limitations of achieving a perfect balance between quality and speed are discussed, emphasizing that true optimality is often context-dependent and contingent on factors like the specific models used and the chosen metrics for evaluation.
Batch SD#
Batch Speculative Decoding (Batch SD) aims to accelerate large language model (LLM) inference by processing multiple draft sequences concurrently. Instead of validating each token sequentially, as in standard Speculative Decoding, Batch SD generates several candidate sequences from a smaller, faster model, then evaluates them in parallel using the LLM. This parallel processing significantly reduces the total inference time. Key advantages include improved efficiency through parallelization and potential reduction in the number of rejections, which arise when a small model’s prediction is deemed incorrect by the LLM. However, the optimal batch size remains an open question, with theoretical analysis suggesting that while increasing batch size generally improves efficiency, it does not scale indefinitely. A trade-off exists between inference speed and the quality of the final output as overly aggressive batching can impact the accuracy of the final result. Future research should investigate efficient strategies for determining optimal batch size, given the specific characteristics of the large and small models involved, and the desired output quality.
Bias-Rejection Tradeoff#
The bias-rejection tradeoff in speculative decoding explores the inherent tension between maintaining output quality (low bias) and achieving faster inference (fewer rejections). Reducing rejections often requires accepting tokens from the draft model that might deviate from the large model’s ideal distribution, thus increasing the bias. The optimal balance depends heavily on the divergence between the draft and large models: similar distributions allow for more aggressive speculation (fewer rejections), while dissimilar distributions necessitate a conservative approach, accepting only high-confidence predictions. This tradeoff is formalized in optimization models that aim to find the Pareto front, highlighting the best achievable combinations of bias and rejection rates. Theoretical results show fundamental limits to inference acceleration dependent upon the initial model divergence. Practical algorithms, therefore, must carefully balance these factors, adjusting acceptance probabilities to achieve desired levels of quality and speed.
Future Work#
The ‘Future Work’ section of a research paper on speculative decoding for large language models (LLMs) could explore several promising avenues. Extending the framework to handle non-autoregressive decoding methods is crucial, as these offer potential speed improvements. Investigating the optimal balance between draft model complexity and accuracy would refine the trade-off between speed and output quality. Developing robust theoretical bounds for batch speculative decoding is needed to better understand its efficiency and scalability. Exploring the application of speculative decoding to different modalities beyond text, such as image and video generation, presents exciting opportunities. Finally, empirical evaluation on a broader range of LLMs and tasks is essential to demonstrate the generalizability and effectiveness of the proposed techniques.
More visual insights#
More on figures
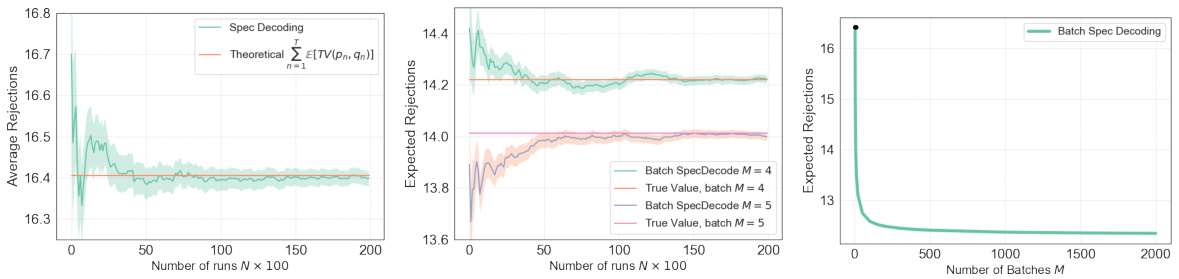
This figure displays simulation results that compare empirical and theoretical results of speculative decoding and batch speculative decoding. The left panel shows a simulation of standard speculative decoding, demonstrating the convergence of empirical average rejections to the theoretical value predicted by Theorem 1. The middle panel presents simulations of batch speculative decoding with different batch sizes (M=4 and M=5), again comparing empirical and theoretical results (this time using Theorem 3). Finally, the right panel illustrates the scaling law of expected rejections for batch speculative decoding as a function of batch size (M), showing the convergence to a limit as M increases.
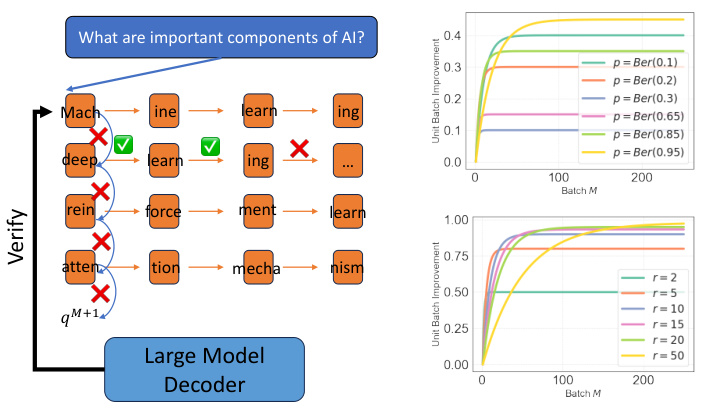
The left panel shows the process of Batch Speculative Decoding. Multiple draft sequences are generated in parallel, and the large model verifies them. The right panel displays two graphs showing the relationship between batch improvement and batch size (M) for two different scenarios. The upper graph uses Bernoulli distributions for p and q, while the lower graph uses uniform distributions. Both graphs illustrate that the benefit of increased batch size diminishes as M increases.

This figure shows the Pareto front between rejection probability and distribution bias. The left panel shows the Pareto optimal tradeoff between these two metrics. The middle and right panels show a numerical example illustrating this tradeoff, where the over-acceptance threshold is varied. The black line in the left panel represents the optimal deviation given by Theorem 4, showing the minimum distribution bias for a given rejection probability. The unattainable region is the area below the Pareto front, indicating that no algorithm can achieve better performance than what is indicated by the Pareto front.
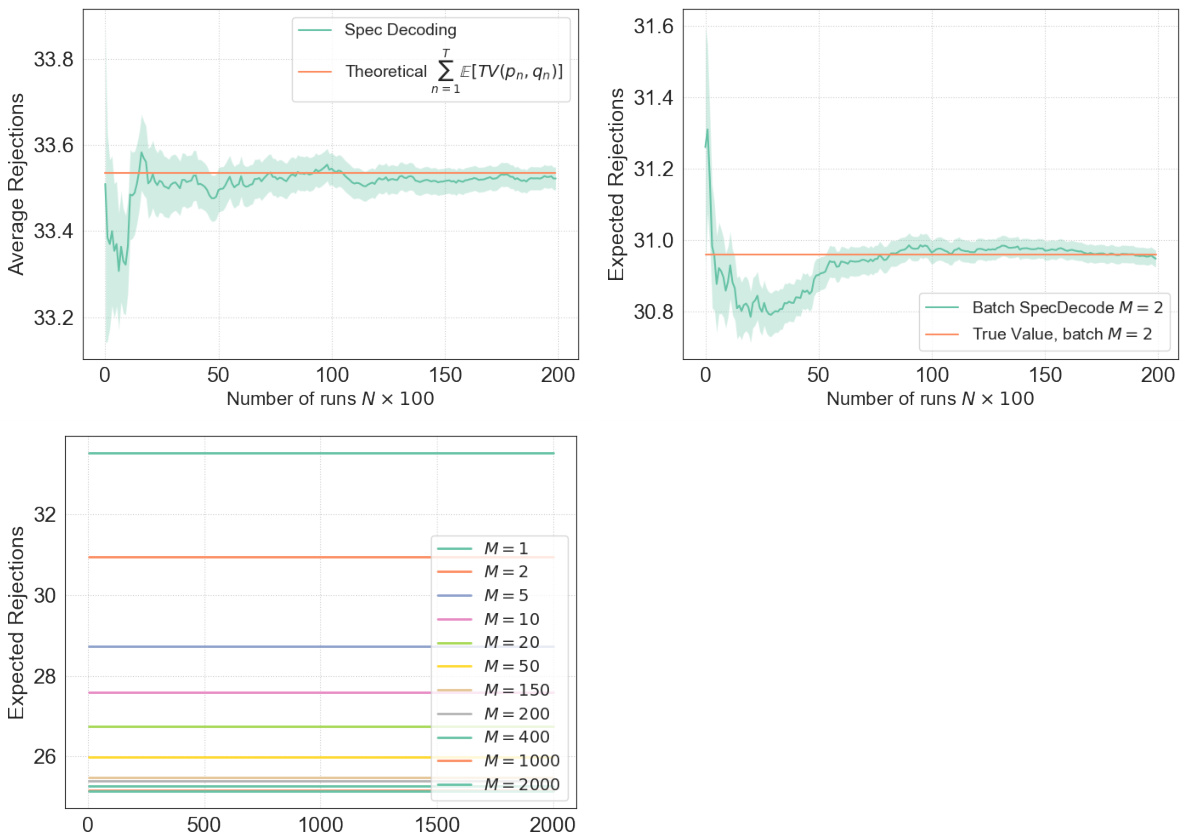
This figure presents simulation results for Speculative Decoding and its batch version. The left panel shows a comparison of empirical and theoretical expected rejections for standard speculative decoding. The middle panel shows similar comparisons for the batch version with different batch sizes (M=4 and M=5). The right panel illustrates how the expected number of rejections scales with increasing batch size (M), demonstrating convergence to a limit.
More on tables

This table compares the performance of two decoding methods, Decoding-OPT and Decoding-UNO, using different over-acceptance thresholds (epsilon values). The WinRate metric shows the percentage of times each method produced a higher-quality response as judged by a score model (either RM-Mistral-7B or GPT-4) across 200 prompts, with 500 comparisons per prompt. Decoding-OPT consistently outperforms Decoding-UNO across various epsilon values and scoring models, demonstrating the effectiveness of the Pareto-optimal solution for output quality and rejection trade-offs.

This table presents the results of an experiment comparing two decoding methods: Decoding-OPT and Decoding-UNO. Decoding-OPT uses the optimal distribution derived in Theorem 4, while Decoding-UNO uses a suboptimal distribution. The experiment measures the ‘WinRate’, which is the percentage of times Decoding-OPT’s responses are preferred by a score model over Decoding-UNO’s responses, for a set of prompts and different values of a hyperparameter (epsilon). The table shows the WinRate for two different score models (RM-Mistral-7B and GPT-4) and different epsilon values.

This table presents the results of a simple experiment comparing two decoding methods, Decoding-OPT and Decoding-UNO, using different over-acceptance thresholds (epsilon). The WinRate metric is used to measure the quality of responses, indicating the percentage of times each method produced a higher-quality response (as determined by a score model) for a set of prompts. The methods use pythia-70m as a draft model and pythia-2.8b as the target model. Two scoring models, RM-Mistral-7B and GPT-4, are used to evaluate the quality of generated responses. The table shows how the choice of epsilon and the scoring model affect the relative performance of the two decoding methods.
Full paper#



















