Safety through feedback in Constrained RL

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is important because it tackles the significant challenge of cost function design in safe reinforcement learning. By introducing a novel approach that uses trajectory-level feedback for cost inference, it presents a more practical and efficient solution to ensuring safe and reliable AI agents, particularly in complex scenarios where traditional cost function design is infeasible. The proposed novelty-based sampling mechanism reduces the burden on human evaluators, which increases the scalability of the approach. This opens up new avenues for research, particularly in safety-critical areas where efficient cost learning is essential.

Visual Insights

#

This figure compares the performance of RLSF, PPO, and PPOLag in three different self-driving scenarios within the Safety Driver environment. The x-axis represents the number of training steps (in millions), and the y-axis shows the cost violation rate. Shaded areas represent the standard error across 6 independent runs for each algorithm. The figure demonstrates the ability of RLSF to achieve a low cost violation rate comparable to PPOLag (which uses the known cost function) while significantly outperforming PPO (which doesn’t incorporate cost).

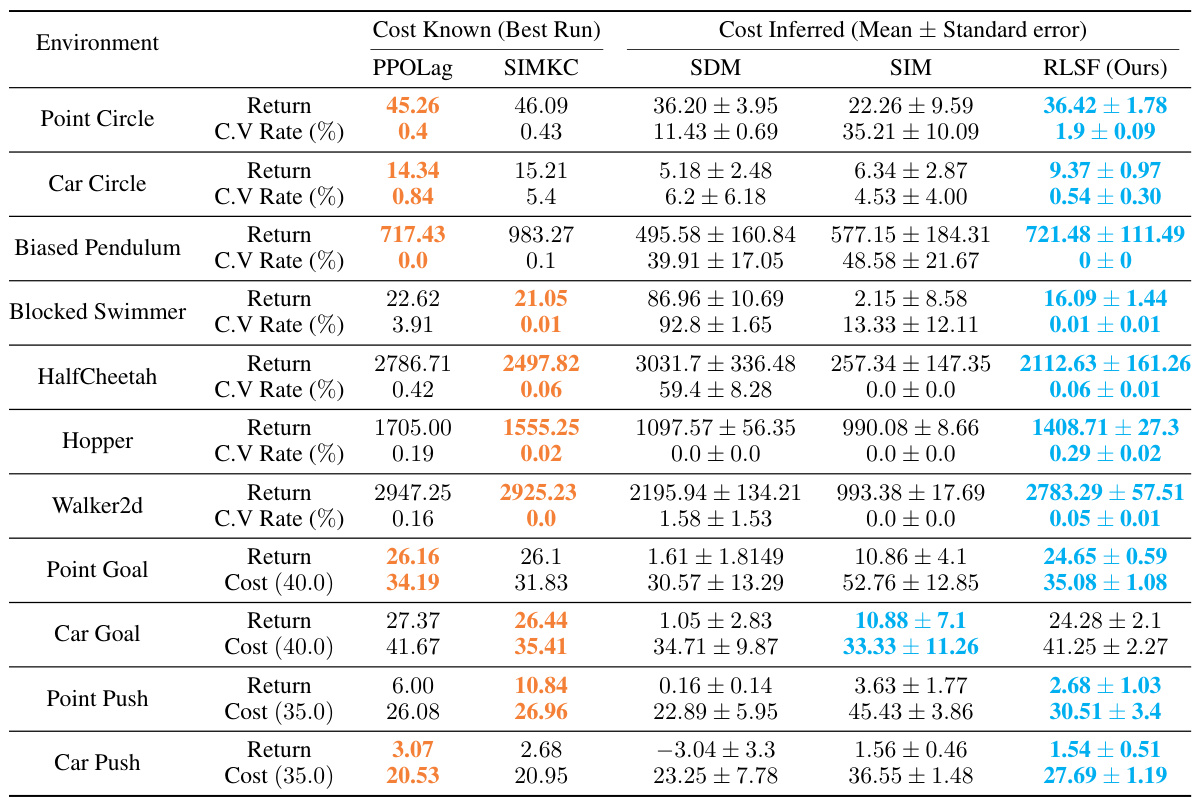
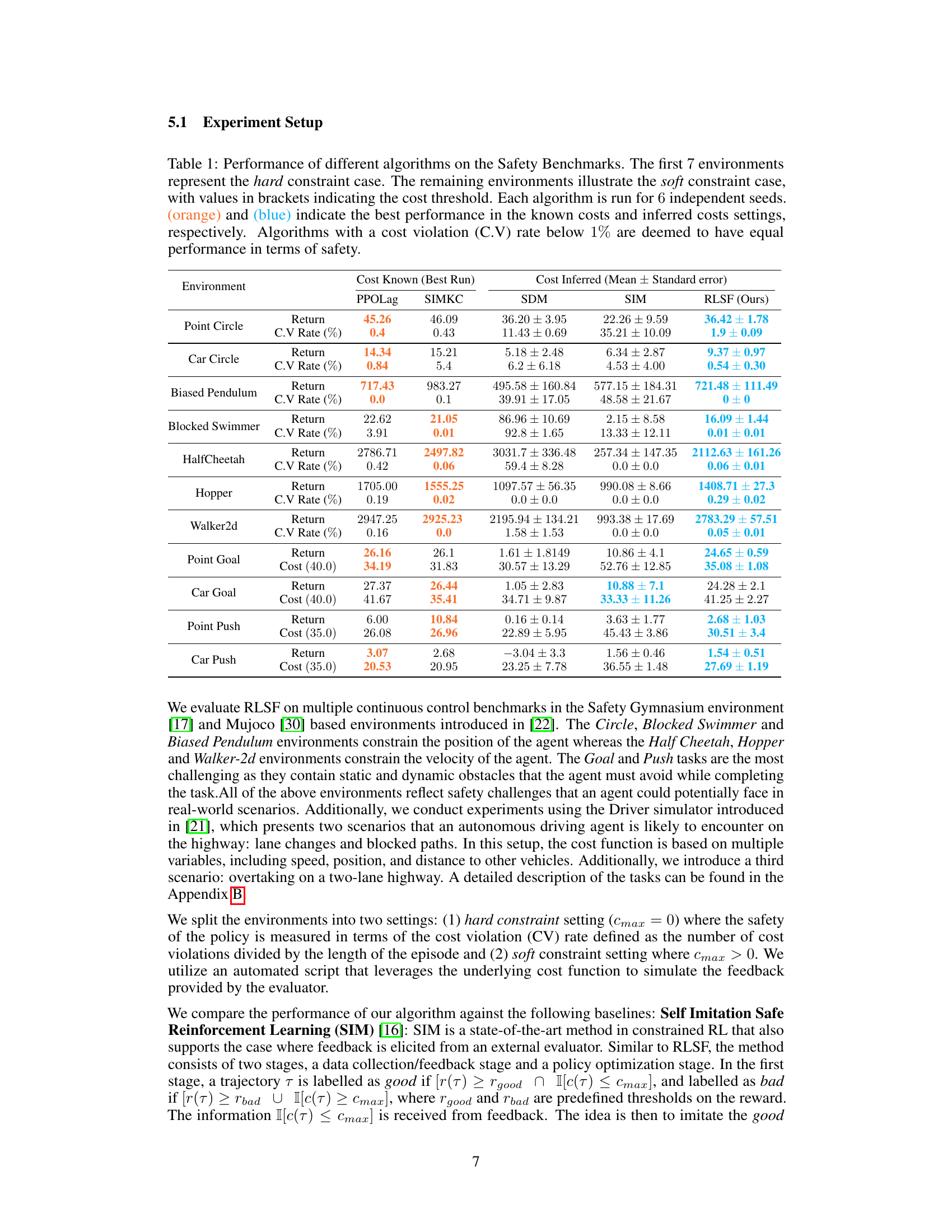
This table presents a comparison of the performance of various reinforcement learning algorithms on safety benchmark tasks. It shows the return and cost violation rate for each algorithm across several environments, distinguishing between those with hard constraints (Cmax=0) and soft constraints (Cmax>0). The best-performing algorithm with known and inferred costs are highlighted. Algorithms with very low cost violation rates are considered equivalent in terms of safety.

In-depth insights

#

Constrained RL via Feedback

#

Constrained reinforcement learning (RL) tackles the challenge of ensuring safe and effective agent behavior in safety-critical applications. A common approach involves incorporating a cost function alongside the reward, penalizing unsafe actions. However, designing appropriate cost functions can be extremely difficult and resource-intensive. Feedback-based methods offer a compelling alternative, where the cost function is learned implicitly from feedback provided by a human evaluator or a surrogate system. This feedback can be given at various levels of granularity, from individual state-action pairs to entire trajectories. A key challenge lies in efficiently collecting and leveraging the feedback, as obtaining feedback for each trajectory might not be feasible. Therefore, methods for intelligently selecting which trajectories to present for feedback are needed. This often involves the use of uncertainty or novelty sampling techniques to maximize the information gain from limited human effort. Furthermore, developing robust and efficient algorithms for inferring the cost function from noisy or incomplete feedback is crucial, often requiring a transformation of the problem to make it easier to solve. Surrogate loss functions or other techniques can aid in credit assignment and facilitate the learning process. Finally, the scalability and applicability of feedback-based constrained RL approaches is a crucial consideration, particularly when dealing with complex and high-dimensional environments. The goal is to develop methods that are both effective in learning safe policies and efficient in terms of feedback requirements.

Novelty-Based Sampling

#

The proposed novelty-based sampling method offers a significant improvement over existing query strategies by selectively presenting novel trajectories to the evaluator. Instead of relying on computationally expensive uncertainty estimation or arbitrary sampling schemes, it leverages the inherent intuition that errors are more likely to occur on unfamiliar data points. By focusing feedback collection on such regions, efficiency is maximized, reducing the evaluator’s burden and accelerating learning. The method’s effectiveness is empirically demonstrated by its near-optimal performance on benchmark environments, requiring far fewer queries than comparable techniques. Novelty is defined via state density; trajectories are considered novel if they traverse states rarely encountered during previous data collection rounds. The inherent decreasing querying schedule further enhances efficiency, as the prevalence of novelty naturally diminishes as the agent’s policy refines. This sampling mechanism is robust and intuitive, adapting seamlessly to diverse environments and providing a pragmatic solution to the feedback bottleneck in safety-critical reinforcement learning.

Surrogate Cost Learning

#

Surrogate cost learning tackles the challenge of directly inferring complex cost functions in constrained reinforcement learning (RL) by employing a simpler, approximating surrogate. Instead of learning the true cost function, which is often expensive or intractable to specify explicitly, a more manageable surrogate model is trained, typically a supervised learning model. This model learns to predict cost from readily available data, such as trajectory-level feedback from human evaluators or system-generated labels. This approach is particularly useful when acquiring state-level feedback is impractical due to the high cost or difficulty of the process. The key advantages of this approach are its scalability to complex environments and efficient handling of noisy, trajectory-level feedback. However, a key consideration is the potential bias introduced by the surrogate model. Careful design and evaluation are necessary to ensure the surrogate effectively captures the essential safety aspects of the true cost function, preventing significant deviations in agent behavior and maintaining appropriate safety guarantees. The effectiveness is highly dependent on the quality and quantity of the training data, making data selection strategies crucial for optimal performance.

Cost Function Transfer

#

The concept of “Cost Function Transfer” in reinforcement learning (RL) is intriguing. It proposes leveraging a learned cost function from one task or environment to improve the performance of an RL agent in a related but different task. This is particularly appealing in safety-critical applications where obtaining labeled data for cost function learning can be expensive or even impossible. The core idea is to transfer knowledge about unsafe states or behaviors, encoded in the learned cost function, rather than directly transferring the policy itself. This approach can significantly reduce the need for extensive data collection in new scenarios. However, several critical factors need consideration. The success of cost function transfer highly depends on the similarity between the source and target tasks. If the tasks are too dissimilar, the transferred cost function might not accurately capture the safety-relevant aspects of the target task, leading to poor performance or even unsafe behavior. Another key challenge is generalizability: a cost function effectively learned in one environment might not generalize well to another, even if the tasks appear similar. Furthermore, robustness to noise and uncertainty in the source cost function is crucial as errors can easily propagate into the target domain. Investigating appropriate similarity measures between tasks and techniques for robust cost function transfer are essential for the practical success of this approach. Addressing these challenges would open up exciting possibilities for efficient and safe RL in diverse applications.

Limitations and Future

#

The authors acknowledge several limitations. Feedback collection is expensive, particularly in complex scenarios. The reliance on trajectory-level feedback, while reducing the evaluator’s burden, introduces an overestimation bias in the inferred cost function that may lead to overly conservative policies. While a heuristic bias correction is proposed, it requires additional tuning. Future work should address these issues, potentially by investigating more sophisticated feedback mechanisms and exploring techniques to reduce the overestimation bias. Transferring the inferred cost function to new agents or tasks is a promising area for future exploration, and extending the approach to settings with noisy or inconsistent feedback is also important. Further investigation into the scalability of the method to even larger, more complex environments should be conducted.

More visual insights

#

More on figures

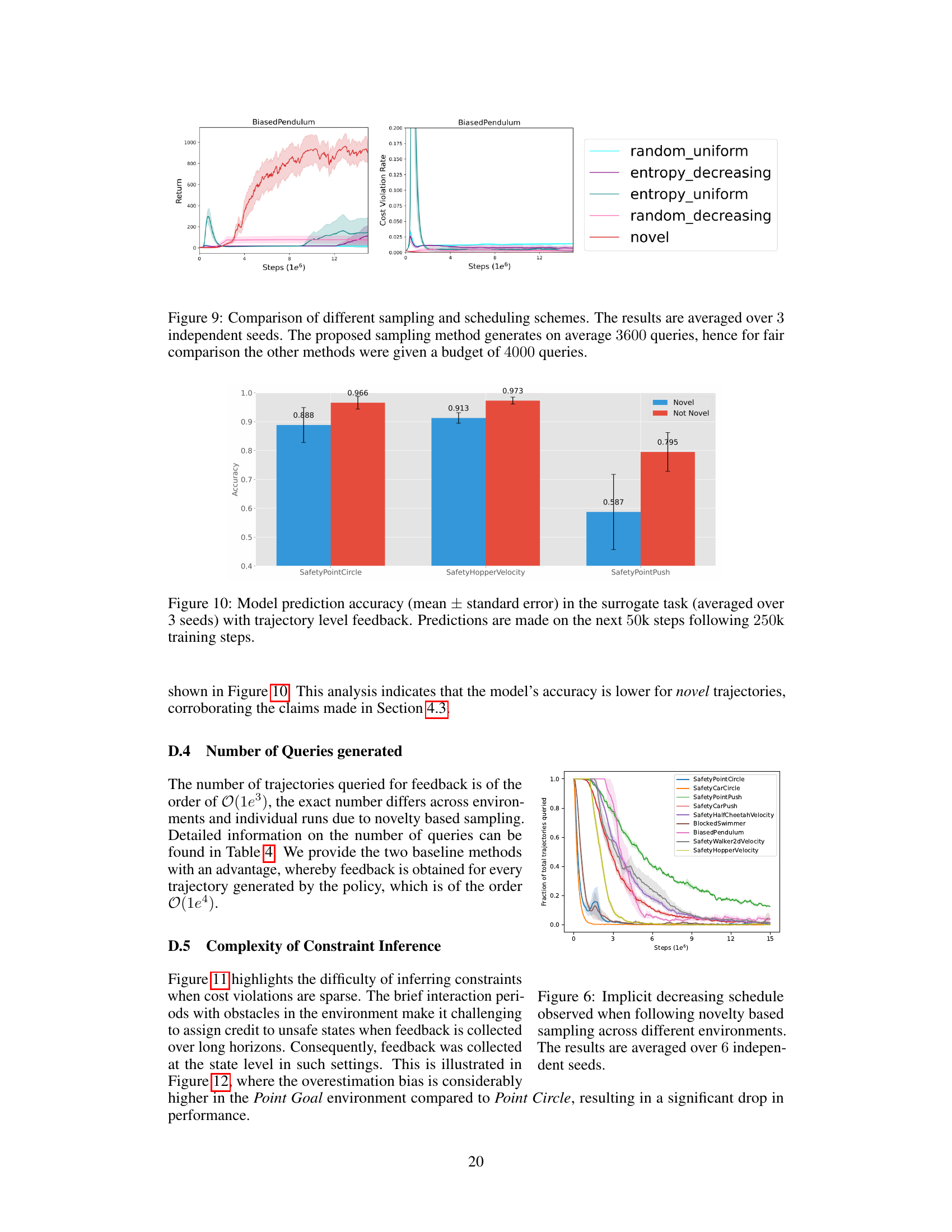
This figure compares the performance of different sampling methods for collecting feedback from an evaluator in a reinforcement learning setting. Five methods are compared: entropy-uniform, entropy-decreasing, random-decreasing, random-uniform, and the novel method proposed in the paper. The x-axis represents training steps (in millions), the left y-axis shows the average return, and the right y-axis shows the cost violation rate. The proposed novel method achieves comparable performance to other methods, with significantly lower cost violation rates and a far lower number of total queries. The shaded areas represent standard error across three independent seeds.

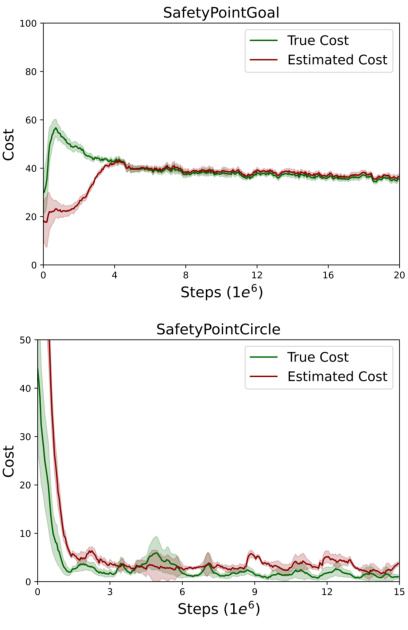
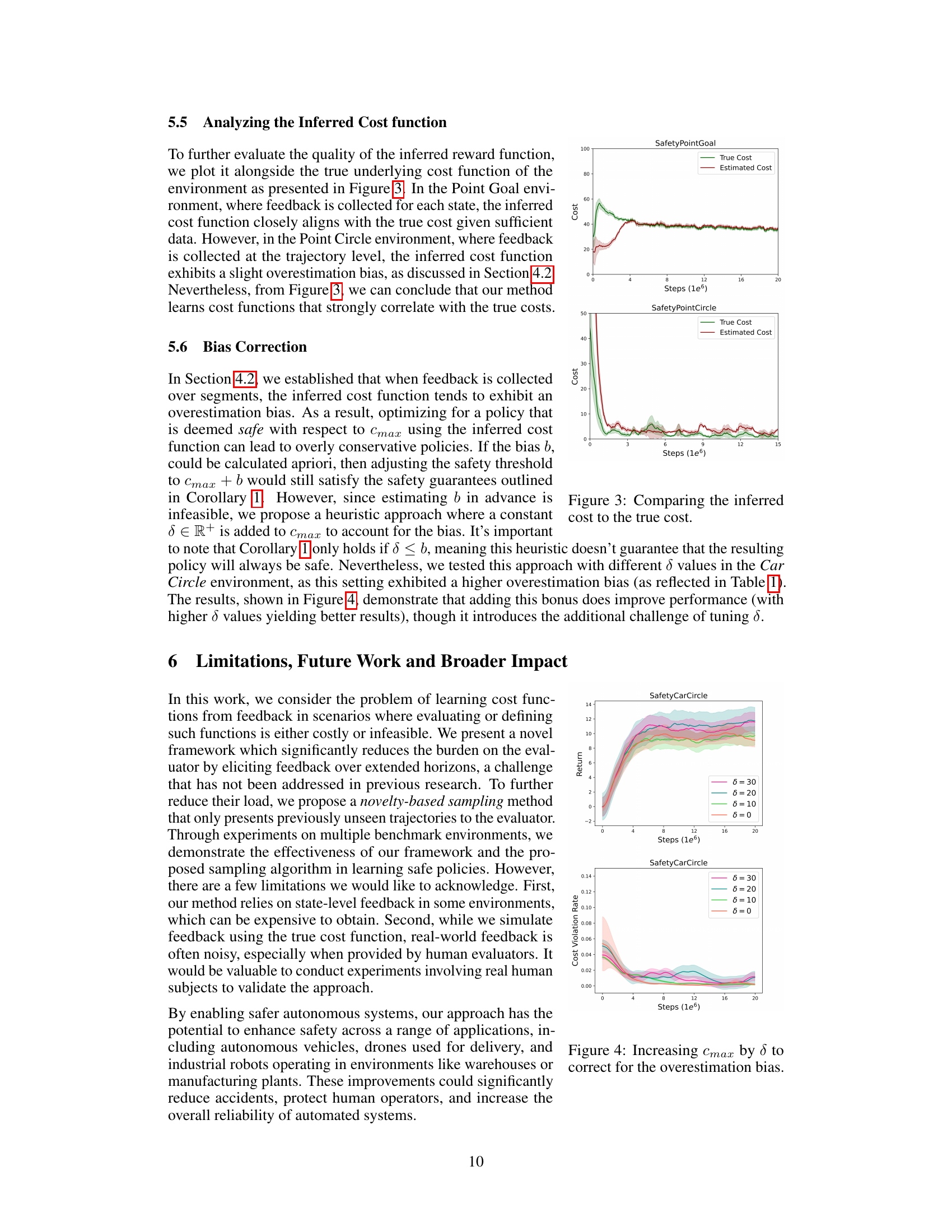
This figure compares the inferred cost function learned by the RLSF algorithm with the actual cost function for two different environments: SafetyPointGoal and SafetyPointCircle. The plots show the mean cost over multiple runs, with shaded regions indicating the standard error. In SafetyPointGoal, the inferred cost closely tracks the true cost. However, in SafetyPointCircle, there is a noticeable overestimation bias in the inferred cost, especially in the earlier stages of training, which gradually decreases over time.

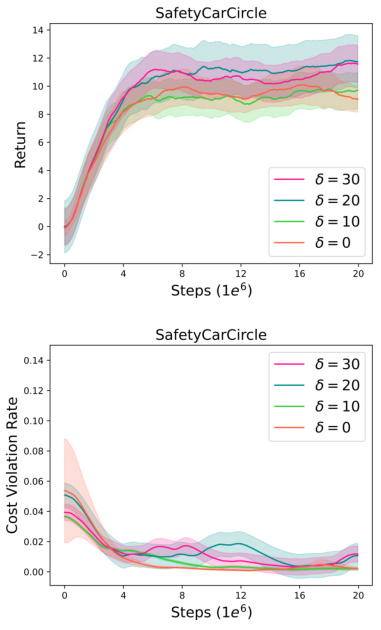
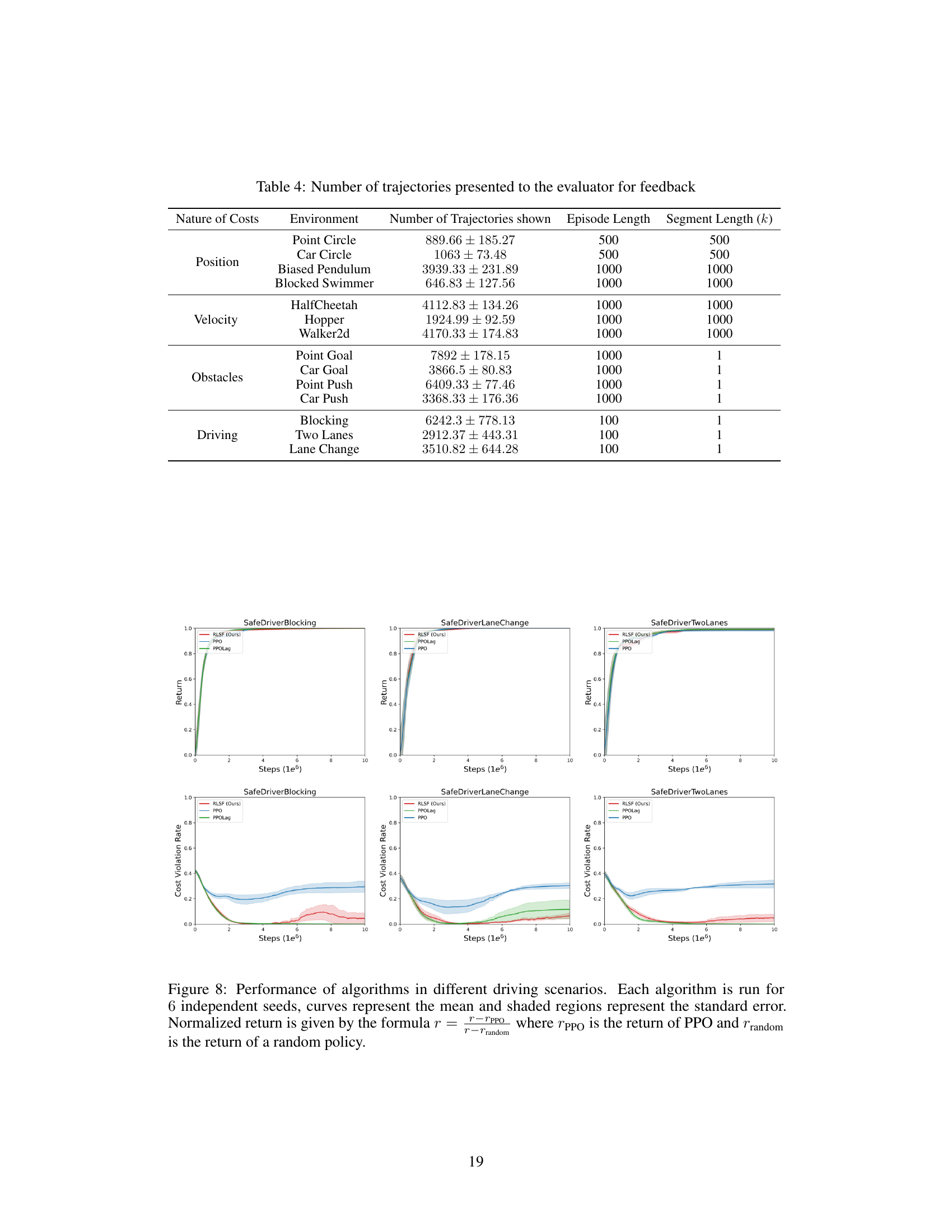
This figure displays the cost violation rates of various reinforcement learning algorithms (RLSF, PPO, PPOLag) across three different driving scenarios within the Driver environment. The x-axis represents the number of steps (in millions), and the y-axis represents the cost violation rate. Each algorithm is evaluated across six independent seeds, with the mean cost violation rate displayed as a line and the shaded region around it indicating the standard error of the mean. This visualization allows comparison of the safety performance of the algorithms over time in complex driving environments.

This figure shows three different scenarios in the Driver environment used in the paper. The scenarios include a blocked road (SafeDriverBlocking), overtaking on a two-lane highway (SafeDriverTwoLanes), and a lane change maneuver (SafeDriverLaneChange). Each scenario presents unique challenges for an autonomous driving agent in terms of safety and efficient navigation.

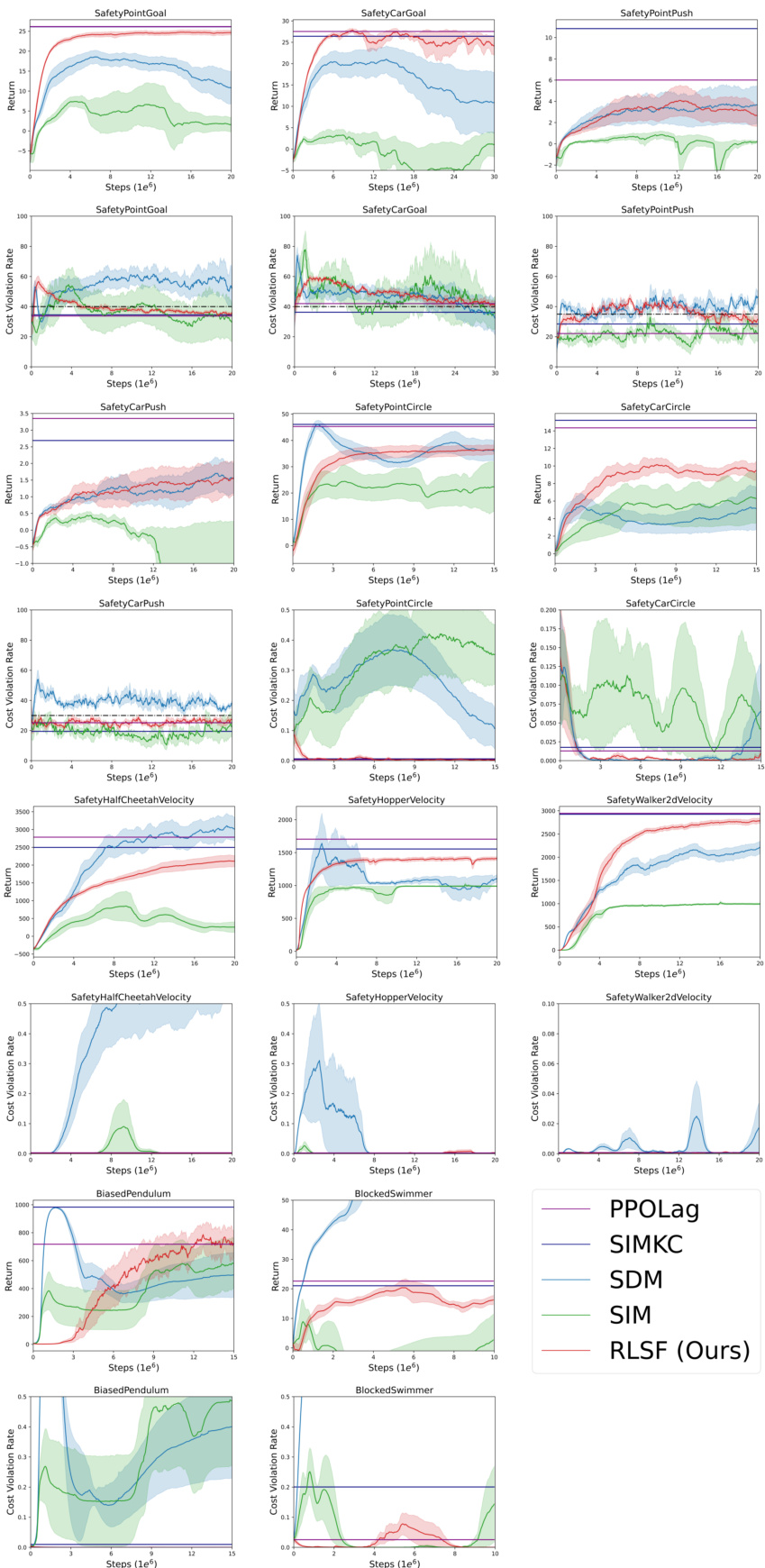
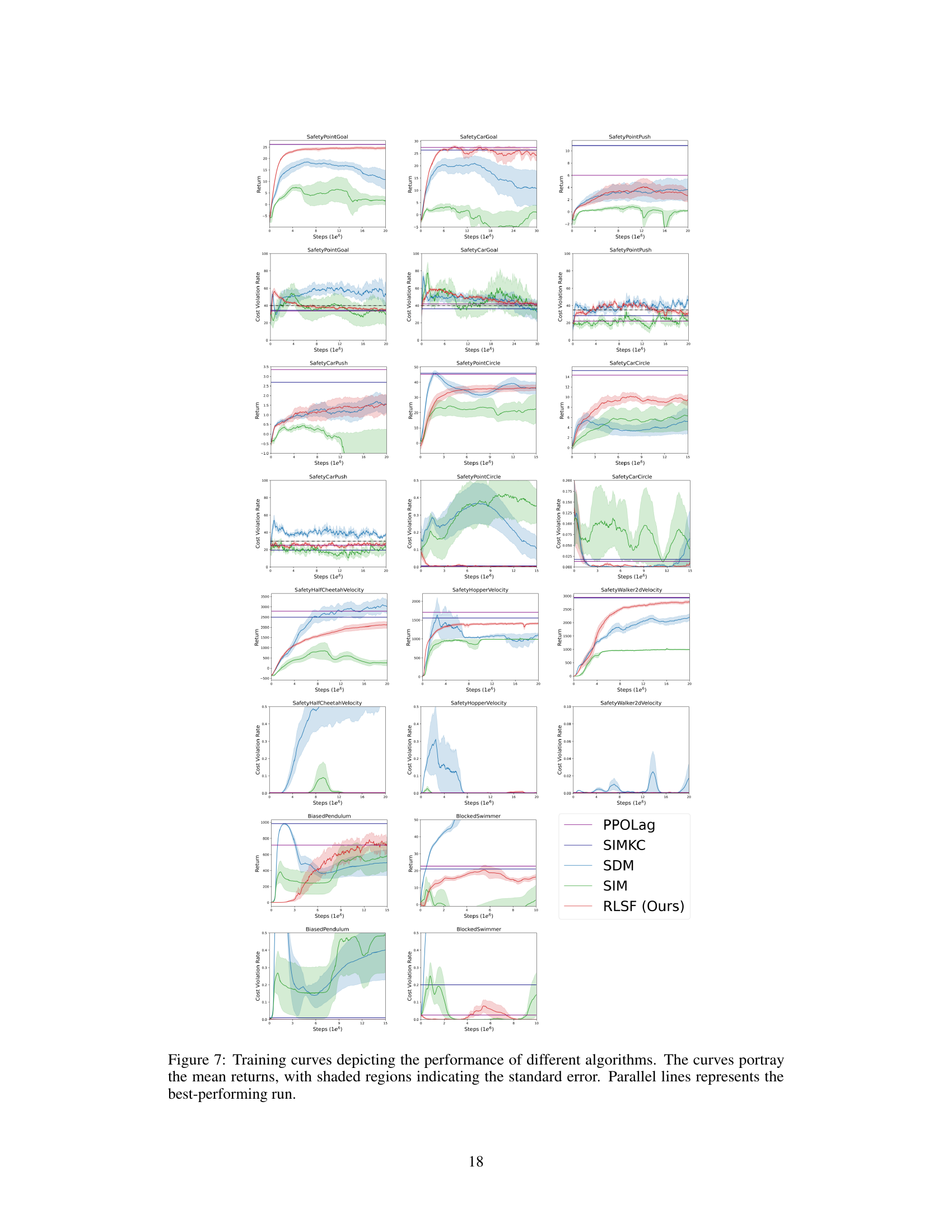
This figure shows the training curves for different reinforcement learning algorithms across various benchmark environments. Each curve represents the average return of an algorithm over multiple independent runs, with shaded areas showing the standard error. The parallel lines indicate the best-performing run achieved for each algorithm. This visualization helps to compare the learning progress and final performance of different algorithms in various constrained reinforcement learning tasks.

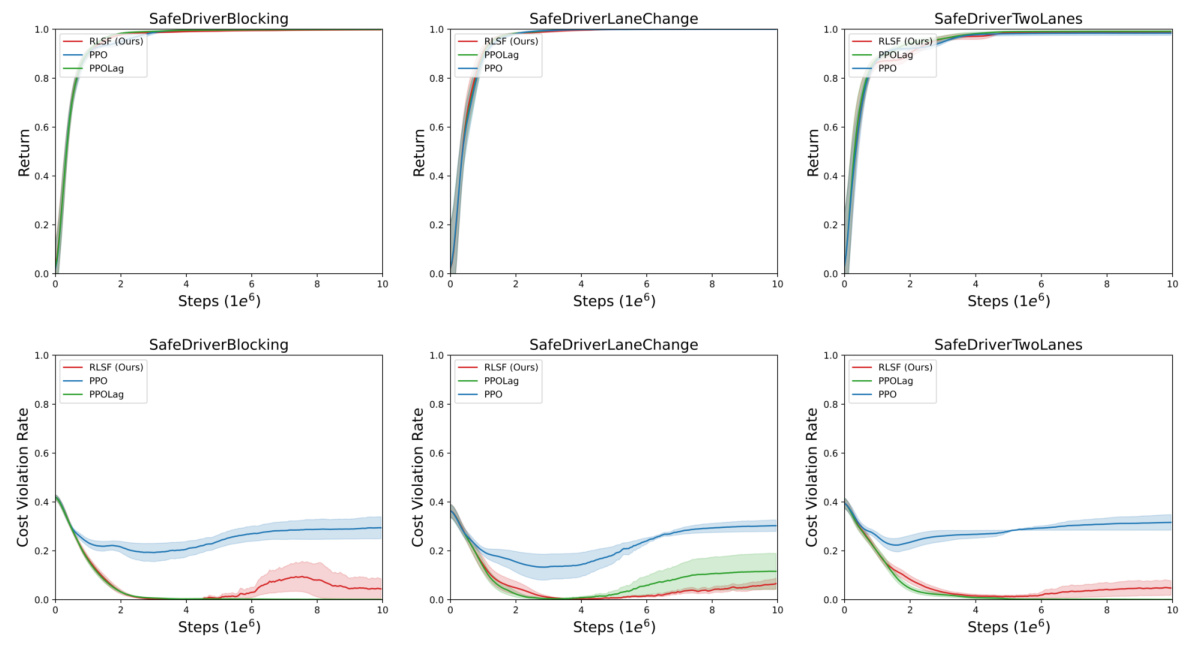
This figure compares the performance of different reinforcement learning algorithms in three self-driving scenarios: lane change, overtaking, and blocked road. The algorithms are RLSF (the authors’ method), PPO (a standard RL algorithm), and PPOLag (a constrained RL algorithm). The graph shows the average return (reward accumulated) and cost violation rate (how often the algorithm violated safety constraints) over multiple runs with independent random seeds. The shaded area around the lines represents the standard error, indicating variability across runs. The normalized return is calculated relative to a random policy. The figure demonstrates RLSF’s superior performance, especially in maintaining safety (low cost violation rate).

This figure compares the performance of different reinforcement learning algorithms across various benchmark environments. Each algorithm’s performance is shown as a curve, representing the mean return over multiple independent runs. The shaded regions indicate the standard error, providing a measure of the variability in the results. Horizontal lines mark the return of a known optimal algorithm, offering a baseline for comparison. The figure displays the algorithms’ ability to achieve high returns in different tasks.

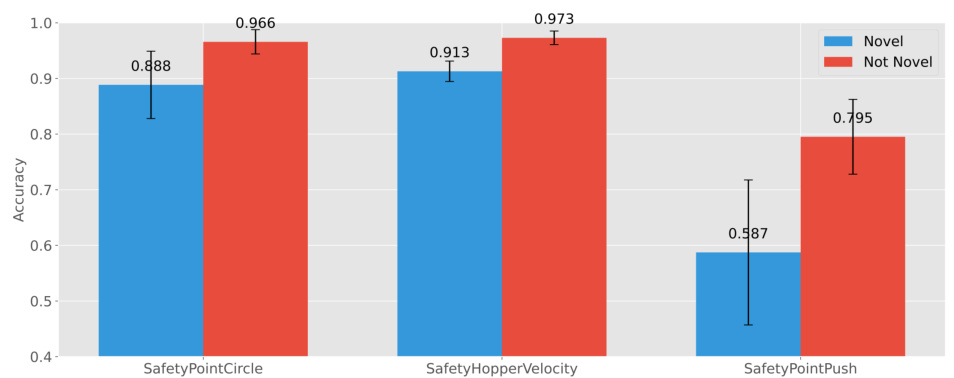
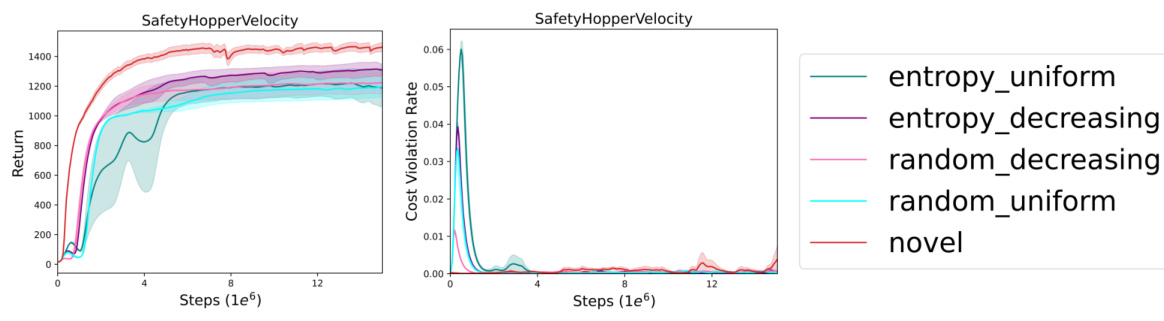
This figure displays the model’s accuracy in a surrogate task using trajectory-level feedback. The accuracy is measured for the next 50,000 steps after 250,000 training steps. It shows a comparison of the model’s performance on novel versus non-novel trajectories. The results indicate that the model is less accurate on novel trajectories, which supports the use of a novelty-based sampling mechanism.

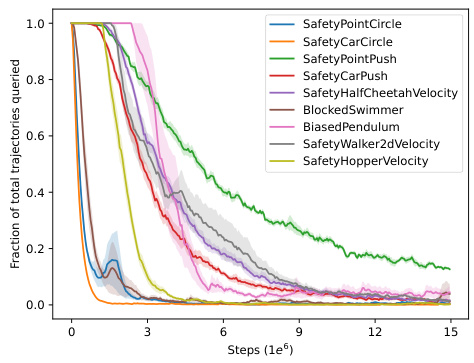
This figure shows the implicit decreasing schedule of queries observed when using novelty-based sampling across different Safety Gym environments. The x-axis represents the training steps (in 1e6), and the y-axis represents the fraction of total trajectories queried for feedback. Each colored line represents a different environment, and the shaded area around each line represents the standard error across 6 independent seeds. The graph shows that the fraction of trajectories queried decreases as training progresses, indicating that the novelty-based sampling mechanism effectively reduces the number of queries needed over time.

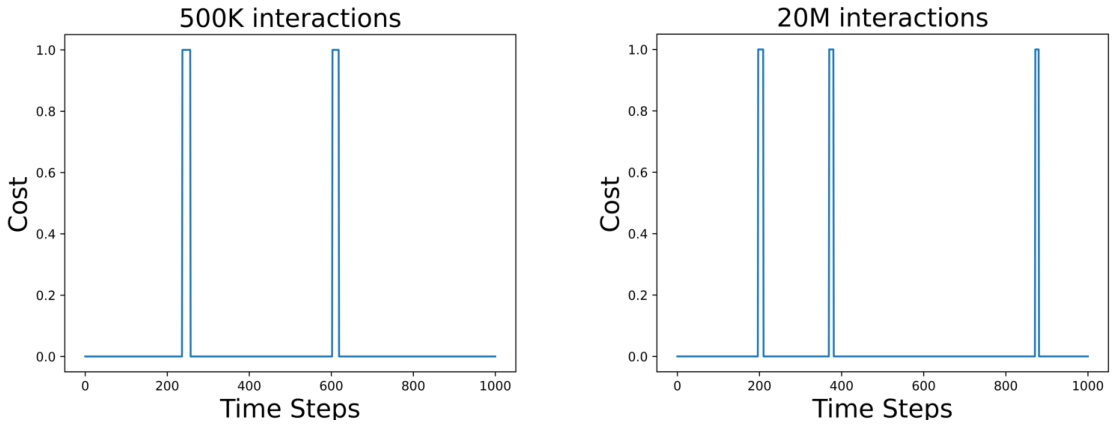
This figure shows the costs incurred by a policy in the Point Goal environment after 500,000 and 20,000,000 training interactions, respectively, over a randomly sampled trajectory. The plots visually depict the cost values over time steps for both interaction counts. It helps to understand how the cost function behaves differently over various stages of training.

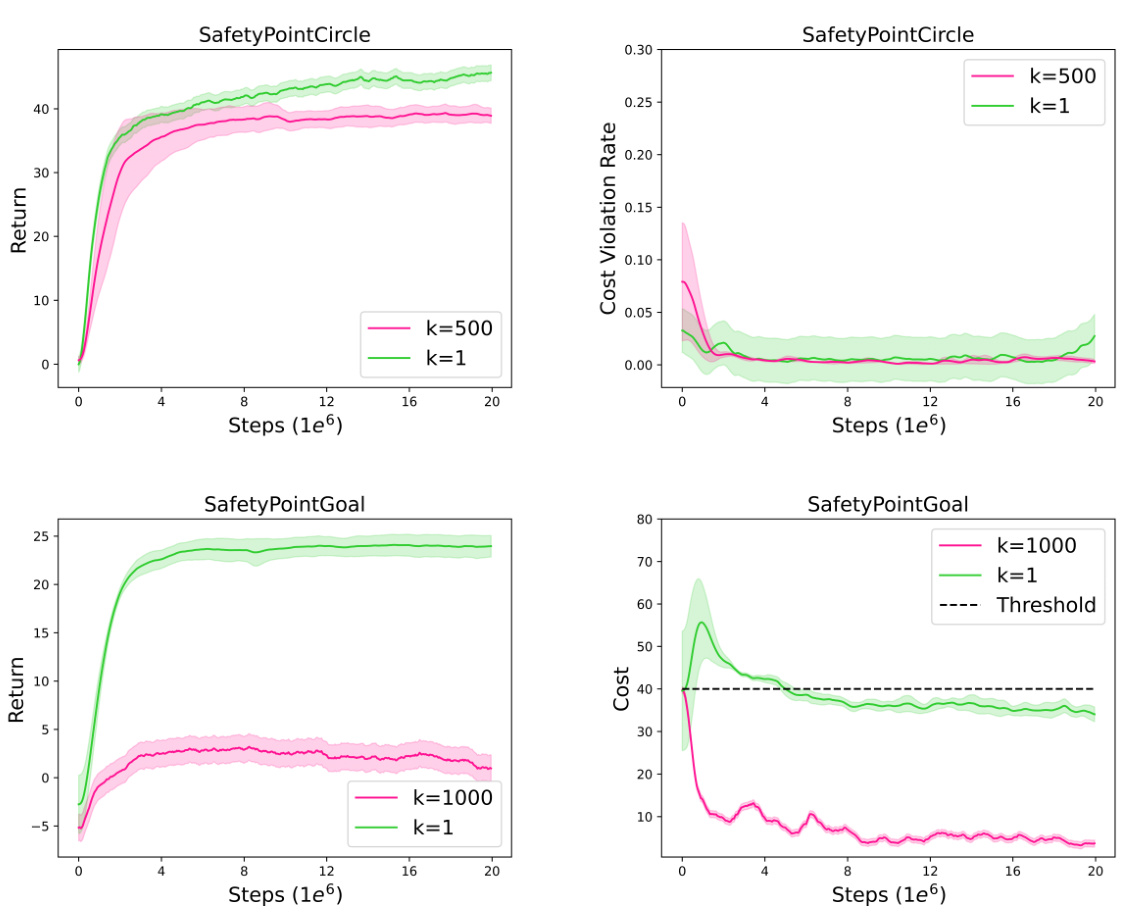
This figure compares the performance of the RLSF algorithm using state-level feedback (k=1, meaning feedback is collected for each state) versus trajectory-level feedback (k=500 or k=1000, meaning feedback is collected for segments of trajectories). The top row shows the results for the SafetyPointCircle environment. The bottom row shows results for the SafetyPointGoal environment. Each subplot shows both return and cost violation rate or cost over training steps. The plots demonstrate the trade-off between efficiency (fewer feedback requests with trajectory-level feedback) and performance (better performance often achieved with state-level feedback).

This figure displays the effect of varying the size of the feedback buffer on the performance of RLSF. It shows training curves for return and cost violation rate for different buffer sizes (100k, 1M, and 4M) across the SafetyPointCircle and SafetyPointGoal environments. The results indicate that smaller buffers (100k) lead to more conservative policies, while larger buffers (4M) achieve better performance.

This figure compares the gradient norms during the optimization of the maximum likelihood estimation (MLE) loss and the proposed surrogate loss. The surrogate loss is designed to address challenges in optimizing the MLE loss, particularly when dealing with long trajectory segments where the probability of a safe trajectory approaches zero, leading to unstable gradients. The plot shows that the surrogate loss produces more stable gradients during training, allowing for smoother convergence and improved performance.

More on tables

This table compares the performance of the PPO-Lagrangian algorithm trained using the true underlying cost function against a version trained using a cost function inferred from a different agent (cost transfer). The results, averaged over three independent seeds, show return and cost violation rate for both scenarios in two environments: Doggo Circle (trained from Point Circle source) and Doggo Goal (trained from Point Goal source). It demonstrates the effectiveness of cost transfer by showing comparable performance with the true cost function.

This table presents a comparison of the performance of different reinforcement learning algorithms on various safety benchmark environments. It shows the return and cost violation rate for each algorithm across multiple environments, categorized into hard and soft constraint cases. The table highlights the best performance achieved with known cost functions and compares it to the performance using inferred cost functions. Algorithms with less than 1% cost violation are considered equally safe.

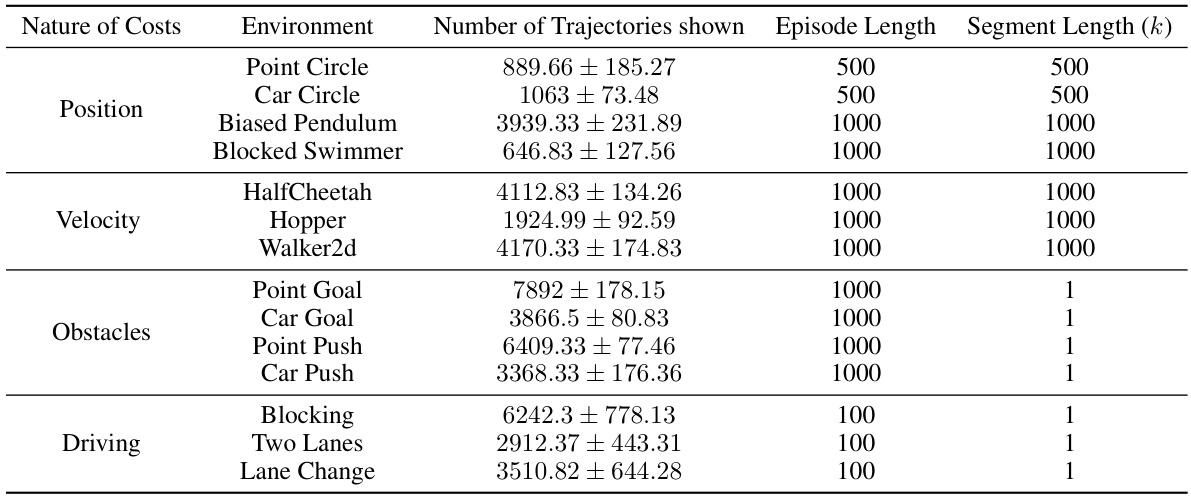
This table presents a comparison of the performance of different reinforcement learning algorithms on various safety benchmark environments. It shows the return and cost violation rate for each algorithm across multiple environments, distinguishing between hard and soft constraint settings. The table highlights the best performance achieved with known and inferred cost functions, indicating the effectiveness of the proposed method (RLSF) in learning safe policies.

Full paper

#