↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many graph applications require efficient computation of Personalized PageRank (PPR) vectors. Existing local methods, while efficient, have runtime limitations. This paper addresses these limitations. The paper explores the potential of localizing standard iterative solvers, which are usually applied globally. These standard solvers are efficient for solving the type of linear systems used in PPR but are not applicable in a large-scale setting because they need to access the whole graph.
This research proposes a novel framework called “locally evolving set process” to effectively localize standard solvers. It demonstrates the effective localization of various solvers, including gradient descent and Chebyshev methods. The framework offers new runtime bounds, which closely mirror the actual performance, and achieves up to a hundredfold speedup on real-world graphs, demonstrating its superior efficiency and applicability to large-scale problems. This significantly advances the field of local graph algorithms and opens up new avenues for optimizing computations on massive graphs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on large-scale graph problems and local algorithms. It introduces a novel framework for characterizing algorithm locality, enabling the development of faster local linear solvers. This is highly relevant to current trends in large-scale data analysis and machine learning where dealing with massive graphs is a significant challenge. The findings pave the way for future research on efficient local methods for various graph problems.
Visual Insights#
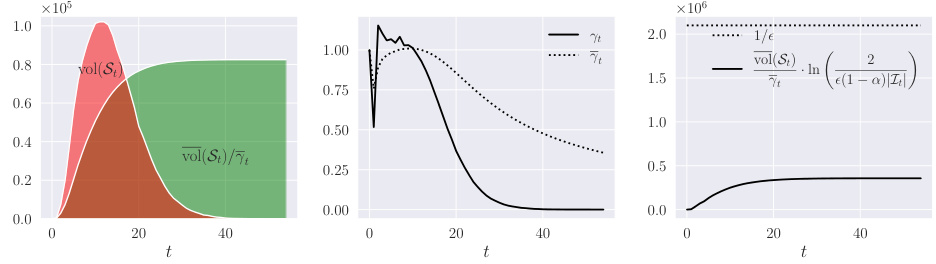
This figure shows the runtime of the Approximate Personalized PageRank (APPR) algorithm in a locally evolving set process. The left panel displays the volume of the active set (St) over time, with the red area representing the total runtime of APPR. The middle panel shows the active ratio (yt) and the right panel displays the ratio of the average volume of active sets to the running average of the residual ratio (vol(ST)/īT). The figure demonstrates that the vol(ST)/īT ratio is always less than 1/e, supporting the theoretical analysis in the paper.

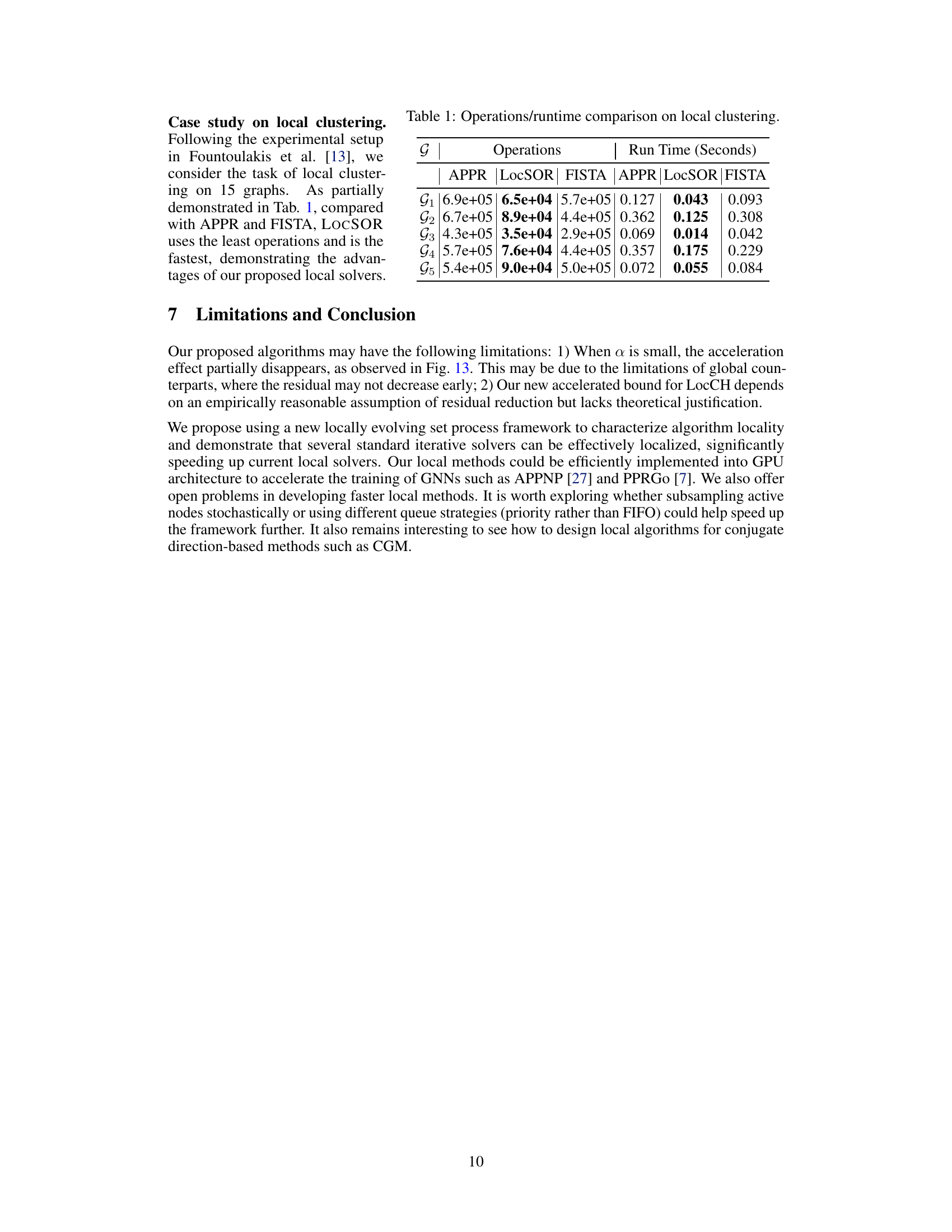
This table presents a comparison of the number of operations and runtime (in seconds) required for local clustering using different methods. The methods compared include APPR, LocSOR, FISTA, and three proposed methods (LocCH, LocHB, and LOCGD). The comparison is performed across five different graphs (G1-G5), providing insights into the relative efficiency of each method for local clustering tasks.
In-depth insights#
Localized Solvers#
The concept of “Localized Solvers” in the context of graph algorithms signifies a paradigm shift towards efficiency by focusing computation on a small, relevant subset of the graph, instead of processing the entire structure. This localization dramatically reduces computational complexity, making it feasible to tackle massive datasets. A key challenge addressed by localized solvers is to maintain solution accuracy despite the restricted view of the graph. This is achieved through iterative refinement, progressively incorporating information from neighboring nodes. The success of a localized solver is determined by a balance between computational speed and the quality of the approximated solution. Different approaches exist, each with its strengths and weaknesses, impacting both run-time and accuracy. The runtime bounds and convergence rates of localized solvers are often dependent on specific graph characteristics and problem properties. This necessitates careful consideration of algorithmic design to guarantee both efficiency and precision. Moreover, effective localization strategies significantly benefit from parallelization capabilities, allowing for substantial speedups in practice. The research in this area continually seeks to optimize the trade-off between the scope of localization, the convergence rate, and the final accuracy of the result.
Evolving Set Process#
The concept of an “Evolving Set Process” in the context of iterative methods for solving graph problems, particularly personalized PageRank, offers a novel framework for analyzing algorithm locality and runtime complexity. It elegantly captures the dynamic nature of these algorithms, where the set of active nodes changes iteratively based on residual magnitudes. This framework moves beyond the traditional approach of analyzing runtime based solely on monotonicity properties of residuals, allowing for the analysis of a broader class of iterative methods. The evolving set process facilitates a more nuanced understanding of algorithm locality by focusing on the average volume of active nodes and the ratio of active nodes to the average residual magnitude. The runtime bounds derived using this framework often mirror the observed performance more accurately than previous bounds based solely on the damping factor and error tolerance. Importantly, the evolving set process framework seems to circumvent the limitations associated with monotonicity assumptions often present in earlier methods. This makes it a promising tool for developing and analyzing faster local algorithms for solving graph problems.
APPR Runtime Bound#
The Approximate Personalized PageRank (APPR) algorithm’s runtime is a crucial aspect of its efficiency, particularly when dealing with large-scale graphs. Early analyses established a runtime bound of \Theta(1/(\alpha\epsilon)), where \alpha is the damping factor and \epsilon is the precision tolerance. This bound, while demonstrating independence from graph size, highlights a potential bottleneck for demanding applications requiring high precision or dealing with low damping factors. A key focus of subsequent research has been to improve this bound, aiming for faster local algorithms. This has led to investigations exploring alternative algorithmic approaches and refined analysis techniques. Ultimately, achieving a tighter runtime bound for APPR remains an area of active research, with the potential to unlock further performance gains and expand the applicability of local PPR methods to even more challenging problems.
Accelerated Methods#
Accelerated methods for solving large-scale linear systems, such as those arising in Personalized PageRank (PPR) computation, are crucial for efficient graph analysis. This research explores the localization of standard iterative solvers like Chebyshev and Heavy-Ball methods, improving upon the runtime of existing local methods like APPR. The core idea is a novel framework called the “locally evolving set process,” which elegantly characterizes algorithm locality and circumvents limitations of previous approaches based on monotonicity assumptions. This framework allows for the derivation of new runtime bounds that accurately reflect the practical performance of localized methods. The analysis demonstrates that, under certain assumptions (e.g., geometric mean of residual reduction), accelerated methods achieve significant speedups over standard solvers. The efficacy of these accelerated local methods is confirmed through extensive numerical experiments on large real-world graphs, showing up to a hundredfold improvement. The focus is on efficiently approximating PPR vectors, but the presented framework potentially generalizes to other linear systems defined on graphs.
Future Research#
The ‘Future Research’ section of this hypothetical paper could explore several promising avenues. Extending the locally evolving set process framework to other graph problems beyond PPR approximation would be valuable, investigating its applicability to broader linear systems and exploring its theoretical limits. Investigating higher-order neighbor interactions within the framework is crucial, potentially leading to improved efficiency and convergence rates. A key area for improvement would be to rigorously address the challenges of non-monotonicity, developing analytical techniques that overcome the limitations of current monotonicity-dependent analyses. This might involve a deeper investigation of second-order difference equations or alternative mathematical approaches. Finally, experimental validation on even larger-scale datasets and a comprehensive comparison with state-of-the-art local solvers are needed to solidify the proposed methods’ practical effectiveness. This includes exploring parallelization strategies and assessing their scalability on diverse graph structures.
More visual insights#
More on figures

This figure compares the actual runtime of the APPR and LocSOR algorithms with their corresponding theoretical upper and lower bounds, all plotted as functions of the error tolerance (e). The left panel shows the actual runtimes, highlighting that LocSOR is significantly faster than APPR for a wide range of error tolerances. The right panel focuses on the theoretical bounds, comparing the upper and lower bounds derived in the paper with Anderson’s existing upper bound. The plot illustrates how the paper’s upper bound is tighter than Anderson’s for small error tolerances, and its lower bound is very effective for larger error tolerances.
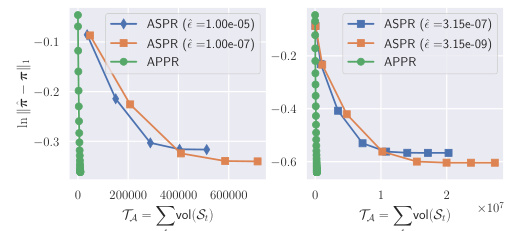
This figure compares the actual runtime of the Approximate Personalized PageRank (APPR) algorithm with that of the proposed Locally evolving set process based GS-SOR (LocSOR) algorithm, as a function of the error tolerance (e). The left panel shows the number of operations required for both methods, while the right panel compares different theoretical runtime bounds (upper and lower bounds for both algorithms, as well as Anderson’s upper bound). The figure highlights the improved runtime of LocSOR compared to APPR, especially when e is relatively large. The results demonstrate the effectiveness of the new runtime bound derived in the paper.

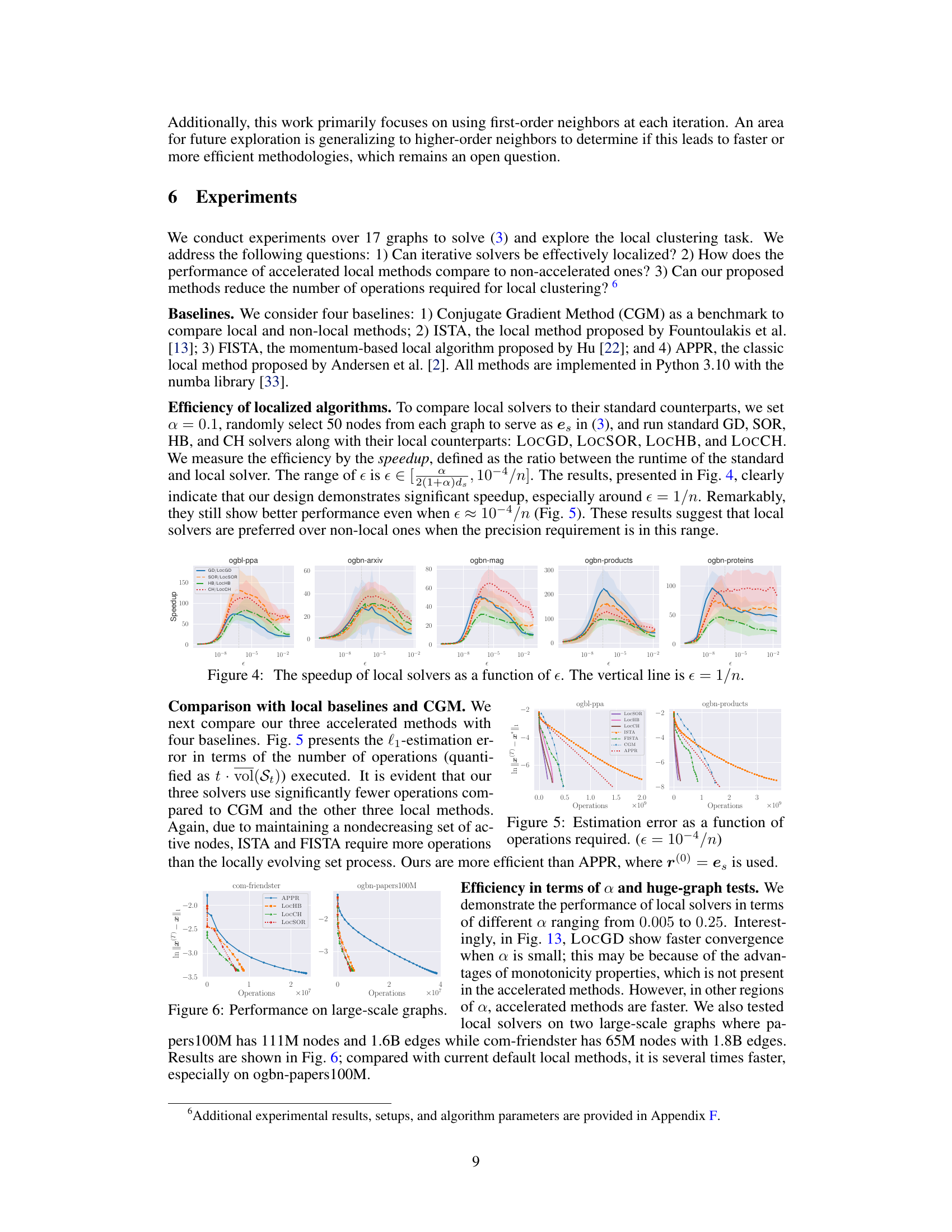
This figure compares the runtime of standard and local solvers for different values of epsilon (ε). The x-axis represents the epsilon value, and the y-axis is the speedup, which is calculated as the ratio of the standard solver’s runtime to the local solver’s runtime. The vertical line at ε = 1/n highlights a significant performance difference. The graph shows that the local solvers (LocGD, LocSOR, LOCHB, LOCCH) are significantly faster than their standard counterparts (GD, SOR, HB, CH), particularly when ε is close to 1/n. This demonstrates that the local solvers are significantly more efficient when the precision requirements are high.
This figure compares the actual runtime of APPR and LocSOR with their theoretical runtime bounds. The left panel shows the actual number of operations performed by APPR and LocSOR for different values of epsilon (error tolerance), while the right panel shows the theoretical upper and lower bounds on the runtime of the algorithms as a function of epsilon. The results show that LocSOR is significantly faster than APPR, and that its actual runtime closely matches the theoretical lower bound. The figure also highlights the superiority of the proposed algorithm over existing local methods.
This figure compares the actual runtimes of the Approximate Personalized PageRank (APPR) algorithm and the proposed Localized Successive Overrelaxation (LocSOR) algorithm against theoretical runtime bounds. The left panel shows the runtime in terms of the number of operations for both algorithms as a function of the precision tolerance (e). The right panel visualizes the upper and lower runtime bounds derived in the paper in relation to the tolerance (e) and the actual number of operations performed. This comparison demonstrates the improved efficiency of LocSOR, particularly when e is relatively small.
This figure compares the actual runtime of APPR and LocSOR with their theoretical upper and lower bounds for varying values of epsilon (e). The left panel shows a comparison of actual runtimes on a specific graph, highlighting the significant speedup achieved by LocSOR over APPR. The right panel visualizes the theoretical bounds, illustrating how the new bounds presented in the paper are tighter than existing bounds, especially for small values of epsilon.

The figure shows the speedup achieved by using local solvers (LocGD, LocSOR, LocHB, and LOCCH) compared to their standard counterparts (GD, SOR, HB, and CH). The speedup is calculated as the ratio of the runtime of the standard solver to the runtime of the corresponding local solver. The x-axis represents the error tolerance (epsilon), and the y-axis represents the speedup. The results demonstrate that local solvers can significantly accelerate the computation, especially when epsilon is close to 1/n. This highlights the effectiveness of localization in improving efficiency.

This figure compares the actual runtime of APPR and LocSOR with their theoretical runtime bounds as a function of the error tolerance (e). It shows that the new upper bound for LocSOR is tighter than the existing upper bound for APPR, particularly when e is small. The lower bounds for both are more effective when e is relatively large. The plot highlights the improvement in runtime efficiency offered by LocSOR compared to APPR, especially in low-error scenarios.

This figure compares the actual runtime of the APPR algorithm with that of the LocSOR algorithm. It also displays the upper and lower bounds calculated for the runtime of these algorithms as a function of the error tolerance (e). The left graph shows how the runtime differs between APPR and LocSOR; the right graph shows the theoretical upper and lower bounds for the runtime of APPR and illustrates how the proposed upper bound compares to the existing upper bound from the literature.

This figure compares the actual runtime of the APPR and LocSOR algorithms with their theoretical upper and lower bounds as a function of the error tolerance (e). The left panel shows the actual number of operations, while the right panel shows the corresponding bounds. It demonstrates that the proposed LocSOR algorithm significantly outperforms the existing APPR approach for smaller values of e, aligning with the theoretical predictions.
This figure compares the actual runtime of the Approximate Personalized PageRank (APPR) algorithm and the proposed Localized Successive Overrelaxation (LocSOR) algorithm. The left panel shows the performance of APPR and LocSOR for different values of epsilon (error tolerance), while the right panel shows the theoretical upper and lower bounds for the runtime of both algorithms. The results demonstrate that LocSOR achieves significantly better runtime compared to APPR, particularly for smaller values of epsilon. The figure also shows that the new theoretical bounds developed in the paper accurately reflect the performance of the algorithm.
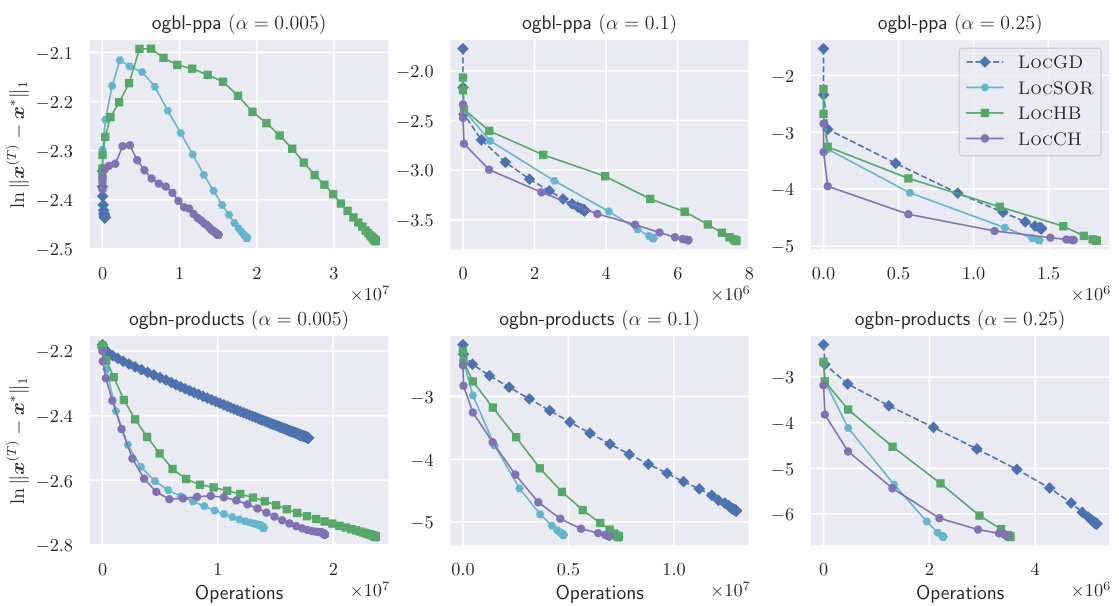
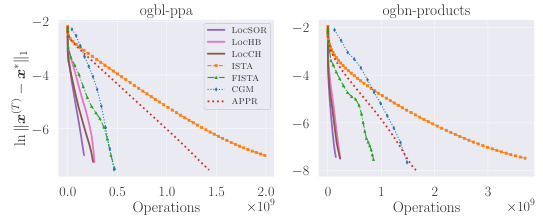
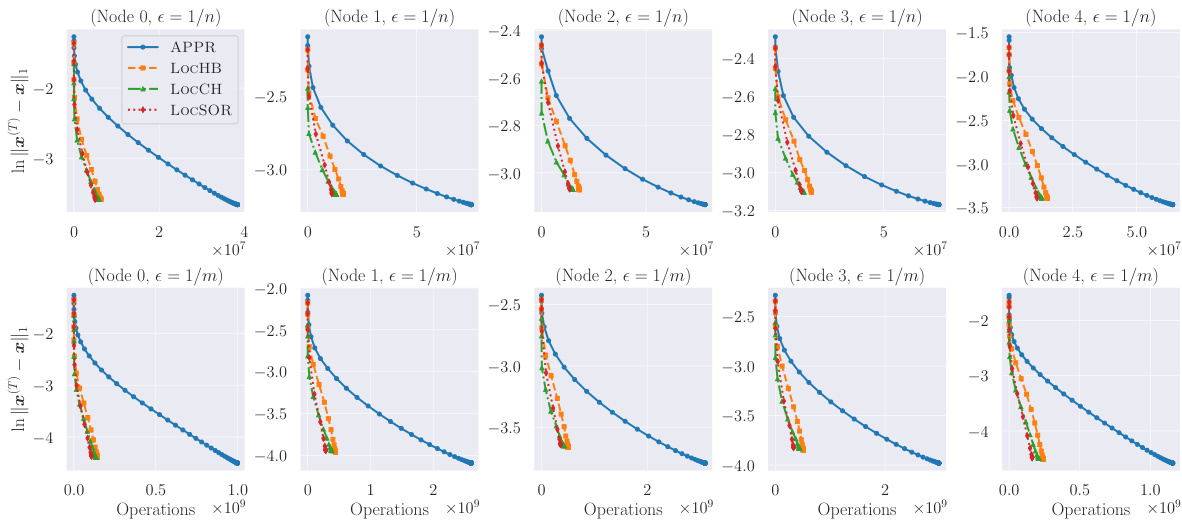
This figure compares the estimation error (in terms of log10 scale of ||x(T) - x*||1) against the number of operations for different values of the damping factor α (0.005, 0.1, and 0.25) on two large graphs: ogbl-ppa and ogbn-products. It showcases the performance of several localized iterative methods, including LocGD, LocSOR, LOCHB, and LOCCH. The results indicate how the number of operations required to achieve a certain estimation error varies across different methods and damping factors.

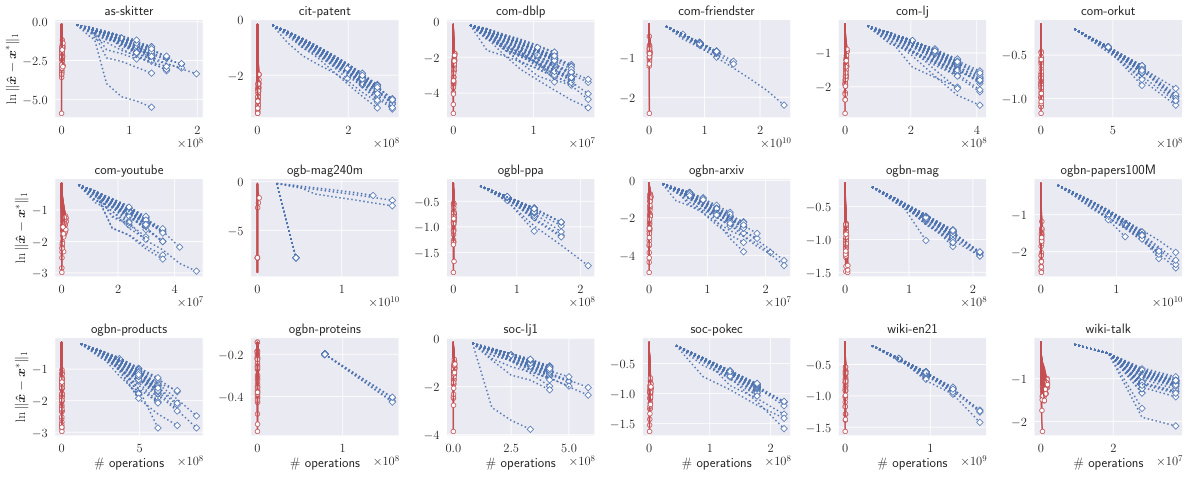
This figure displays the graph conductance achieved by various local clustering methods across 15 different graphs. The conductance is a measure of how well-connected a cluster is, with lower values indicating stronger connectivity. The methods compared include APPR, LocCH, LocHB, LocSOR, ISTA, and FISTA. The figure illustrates the performance of each method in identifying clusters with low conductance. It provides a visual comparison of the effectiveness of the different local clustering algorithms.

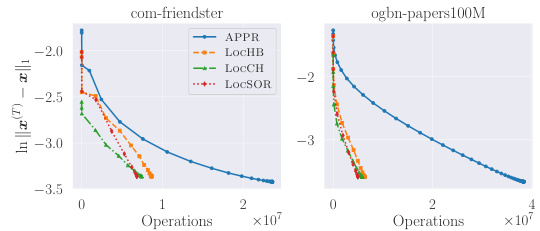
This figure compares the error reduction performance of the proposed LOCCH algorithm against the standard CGM algorithm on the papers100M dataset. The x-axis represents the number of operations needed, and the y-axis represents the logarithm of the error (||x̂-x*||1). The plot shows that LoCCH achieves a significantly faster error reduction than CGM, demonstrating its efficiency in solving large-scale linear systems.
More on tables
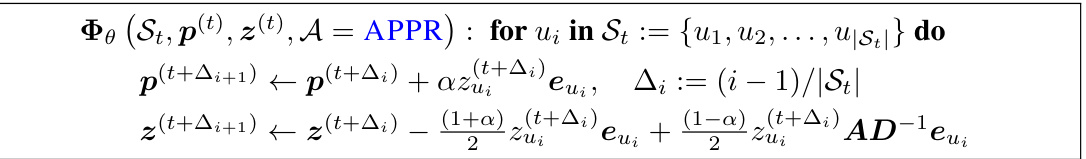
This table presents a comparison of the number of operations and runtime (in seconds) required by different local solvers for the local clustering task. The solvers compared include APPR, LocSOR, FISTA, and others. The table shows that LocSOR generally requires fewer operations and has faster runtime compared to the other methods, highlighting its efficiency for this specific task.
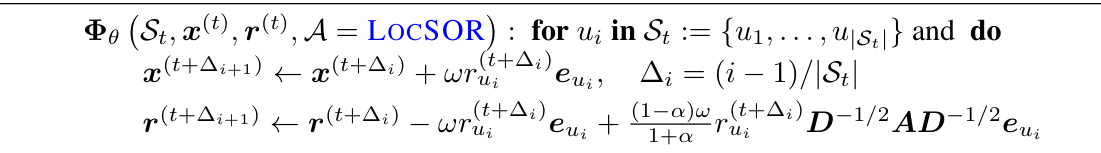
This table presents a case study on local clustering, comparing the performance of various algorithms, including APPR, LocSOR, FISTA, and others, in terms of the number of operations and runtime required. The results show the efficiency of the proposed methods for this task.
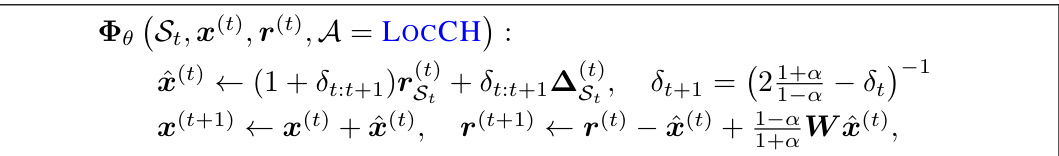
This table presents a case study on local clustering using several methods, including APPR, LocSOR, FISTA, and others. The table compares the number of operations and runtime in seconds needed by each method for local clustering tasks on 5 different graphs. The results highlight the efficiency of LocSOR, which demonstrates the lowest number of operations and fastest execution time among the compared methods, thus demonstrating the advantages of proposed local solvers.
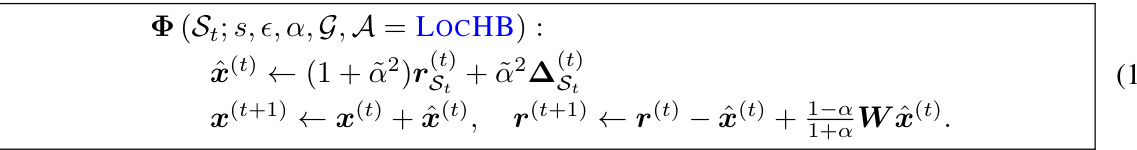
This table presents the runtime in seconds for six different local solvers (APPR, LOCCH, LOCHB, LocSOR, ISTA, and FISTA) on 15 different graph datasets. The error tolerance (epsilon) used for all the experiments was 10⁻⁶. The table provides a direct comparison of the computational efficiency of each method across various graph datasets.
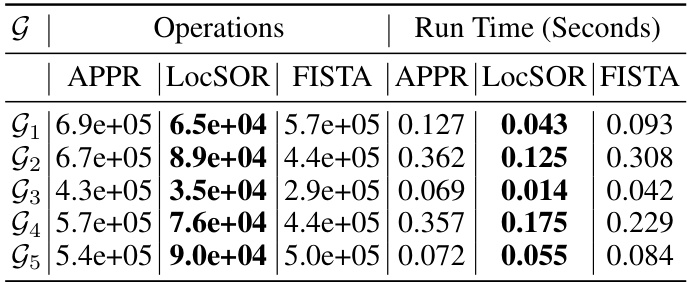
This table presents a comparison of the number of operations and runtime (in seconds) required for local clustering using different methods: APPR, LocSOR, and FISTA. The results are shown for five different graphs (G1 through G5). LocSOR consistently demonstrates a significant reduction in both operations and runtime compared to APPR and FISTA, highlighting its efficiency in local clustering tasks.

This table presents a comparison of the number of operations and runtime (in seconds) for different local clustering algorithms. The algorithms compared include APPR, LocSOR, FISTA, and others. The results are shown for five different graphs (G1-G5), demonstrating the relative performance of each algorithm for this specific task.

This table presents several examples of sparse linear systems that can be reformulated into the target form Qx = b, where Q is a graph-induced matrix and b is a sparse vector. For each original linear system, the table shows the corresponding Q matrix, the vector b, and the spectral bounds of Q’s eigenvalues, along with a reference to the relevant literature.

This table presents the statistics of the 17 datasets used in the paper’s experiments. For each dataset, it lists its name, the number of nodes (n), and the number of edges (m). The datasets vary significantly in size, ranging from relatively small graphs to very large graphs with millions or even hundreds of millions of nodes and edges.
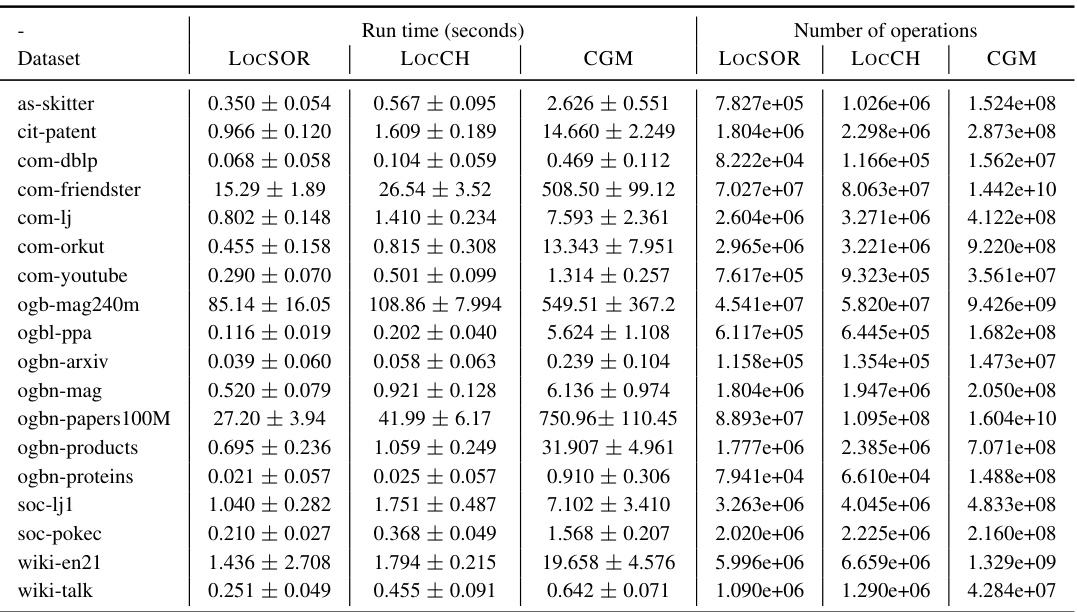
This table presents a summary of the runtime (in seconds) and the number of operations required by three local solvers (LOCSOR, LOCCH, and CGM) across 15 different datasets. The error tolerance (e) is set to 10^-6 for all experiments.
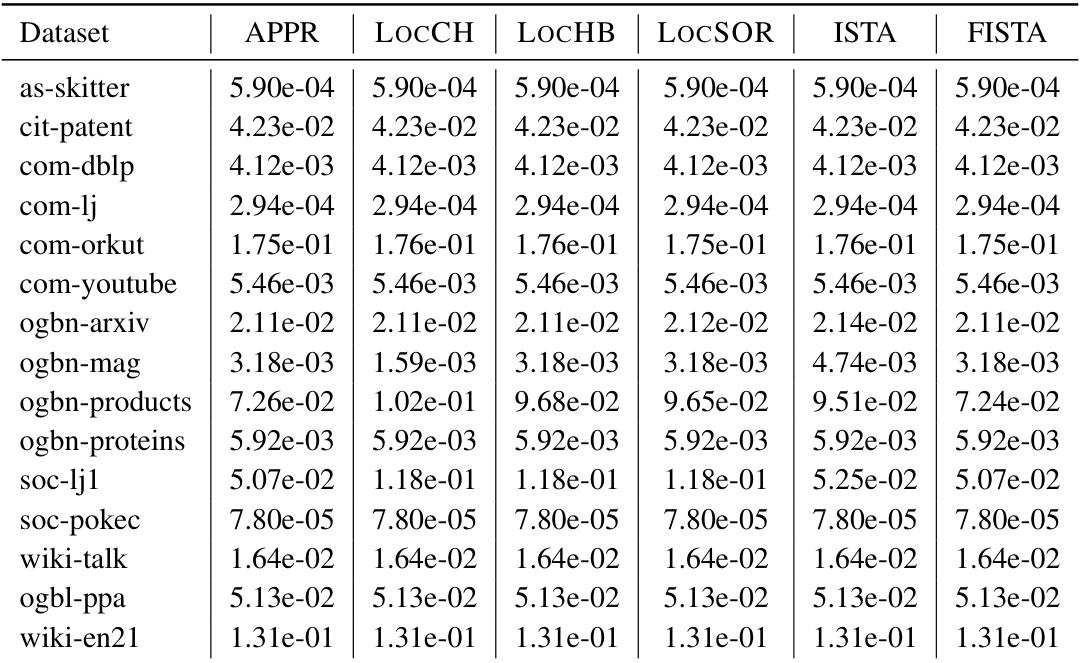
This table presents the local conductance values achieved by six different local solvers (APPR, LOCCH, LOCHB, LocSOR, ISTA, and FISTA) across 15 different graph datasets. The local conductance is a measure of the algorithm’s ability to identify clusters efficiently within a small neighborhood of the graph. A lower conductance indicates better performance. The experiments were conducted with an error tolerance (€) of 10⁻⁶.
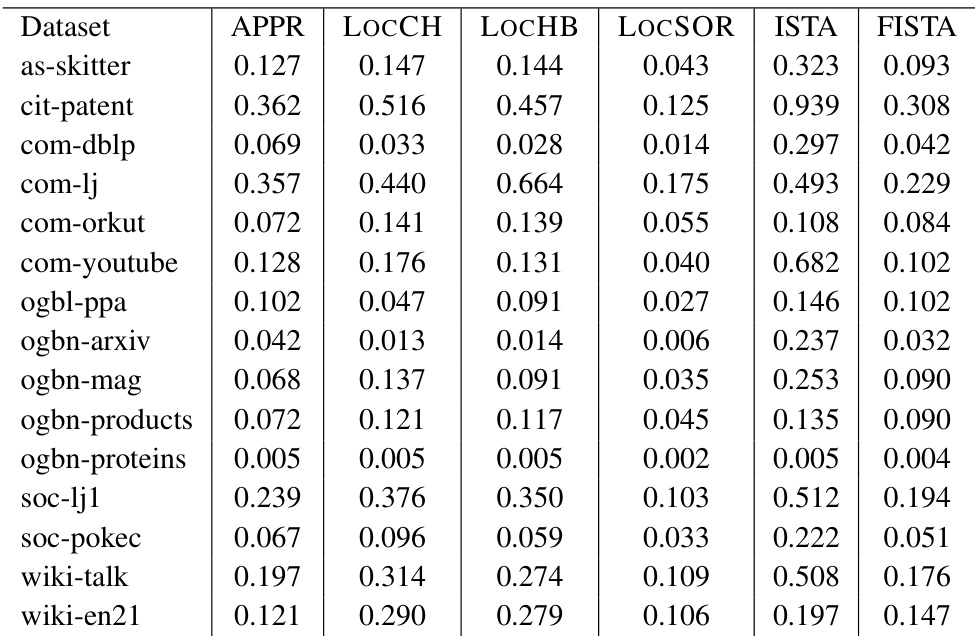
This table presents the runtime in seconds for six different local solvers (APPR, LOCCH, LOCHB, LocSOR, ISTA, and FISTA) on 15 different graph datasets. The runtime is measured for a specific error tolerance (ε = 10⁻⁶). This data allows for a comparison of the computational efficiency of each solver in approximating personalized PageRank vectors.

This table presents the number of operations required for six different local solvers (APPR, LOCCH, LOCHB, LocSOR, ISTA, and FISTA) to perform local clustering on 15 different graphs. The error tolerance (epsilon) is set to 10⁻⁶. The table allows for a comparison of the computational efficiency of these methods in a local clustering task.
Full paper#