↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Zero-sum Markov games (ZSMGs) are a fundamental challenge in reinforcement learning, especially when dealing with continuous state spaces. Existing methods often struggle with the computational complexity and high sample complexity associated with large state spaces. Many algorithms’ sample efficiency depends on the size of the state space, making them impractical for real-world applications. This significantly limits their applicability.
This research introduces Spectral Dynamic Embedding Policy Optimization (SDEPO), a novel natural policy gradient algorithm. SDEPO uses spectral dynamic embedding to effectively approximate the value function for ZSMGs in continuous state spaces. The researchers provide a theoretical analysis demonstrating near-optimal sample complexity independent of the state space size. They also present a practical variant, SDEPO-NN, that handles continuous action spaces effectively and shows strong empirical performance. This is a significant contribution as it improves the scalability and efficiency of solving ZSMGs in real-world scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial because it presents a novel and efficient algorithm for solving zero-sum Markov games with continuous state spaces. This is a significant challenge in reinforcement learning, and the proposed method’s provable efficiency and practical superiority offer substantial advancements. The work opens avenues for research into handling continuous action spaces and scaling to more complex games.
Visual Insights#

The figure shows the convergence speed of three algorithms: SDEPO with random features, SDEPO with Nyström features, and OFTRL. The y-axis represents the duality gap (V** - Vπ,π), which measures the distance from the current policy’s value to the optimal Nash equilibrium. The x-axis represents the number of iterations. The graph demonstrates that SDEPO converges faster than OFTRL for solving this specific random Markov game, highlighting the benefit of the proposed algorithm.
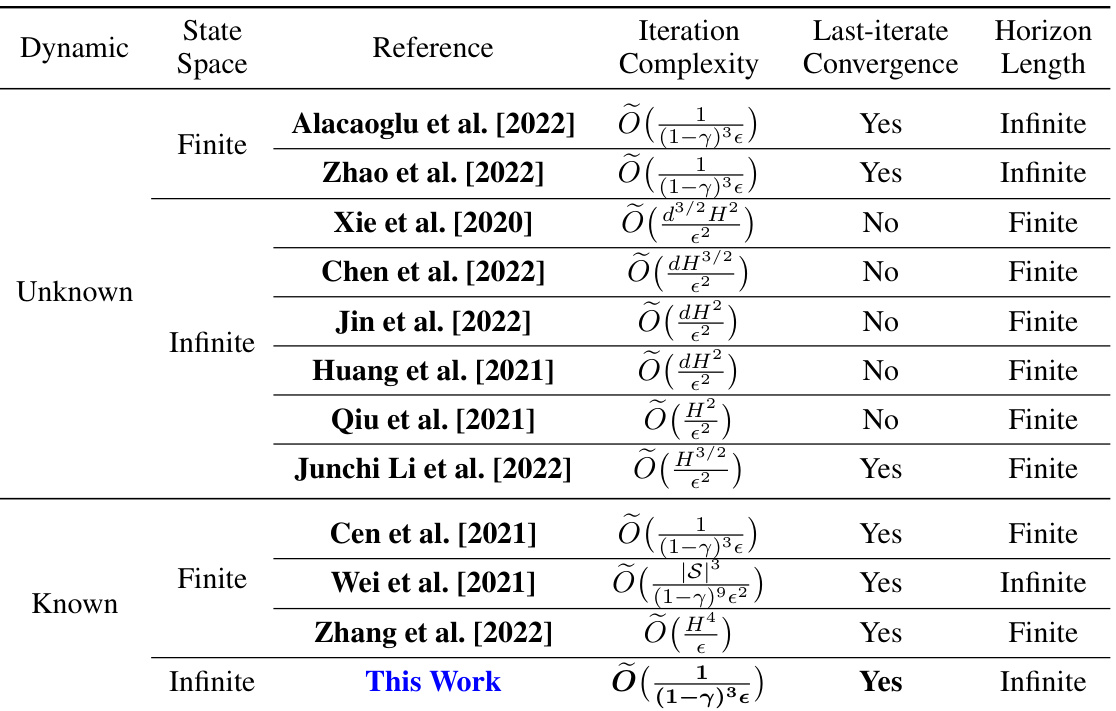
This table compares different policy optimization methods for solving two-player zero-sum episodic Markov games. It shows the iteration complexity, whether the last-iterate converges to the optimal solution, the horizon length, and the state space type (finite or infinite) for each method. The methods are categorized by whether the system dynamics are known or unknown. The table highlights the differences in computational efficiency and convergence properties of various approaches.
Full paper#