Disentangling Linear Quadratic Control with Untrusted ML Predictions

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in control systems and machine learning. It directly addresses the critical challenge of integrating unreliable ML predictions into control policies, offering a novel solution with provable guarantees. This opens avenues for more robust and efficient control systems in various applications, especially those dealing with uncertainty and unpredictable disturbances. The proposed approach is validated through real-world examples, demonstrating practicality and impact.

Visual Insights

#

This figure illustrates the system model used in the paper. An untrusted machine learning agent provides predictions for disentangled latent variables (Šīt(i)). These predictions, along with observed mixed perturbations from previous time steps, are input to the control policy π. The control policy then generates actions (ut) that affect the dynamical system, resulting in an updated state (xt+1).

This table summarizes the key assumptions made in several nonlinear Independent Component Analysis (ICA) models, in addition to the common assumptions that latent variables are mutually independent and at most one latent variable is Gaussian. The assumptions are categorized into those related to the mixing function f and those related to the latent variables s. This helps to clarify the different constraints and conditions imposed by various nonlinear ICA approaches for achieving identifiability of their models.

In-depth insights

#

Untrusted ML Control

#

The concept of “Untrusted ML Control” explores the challenges and opportunities of using machine learning (ML) predictions in control systems when the reliability of those predictions is uncertain. This introduces a significant layer of complexity, as traditional control methods assume accurate models. The core challenge lies in designing control strategies that can gracefully handle inaccurate or noisy predictions while still achieving desired system performance. This requires algorithms that can assess the confidence or trustworthiness of ML outputs and incorporate that assessment into control decisions. A key aspect is developing a balance between leveraging potentially beneficial accurate predictions and mitigating the negative impacts of errors. Robustness and consistency are crucial considerations. Robustness refers to the ability of the control system to maintain stability and achieve acceptable performance despite prediction errors, while consistency implies that the control system performs near-optimally when predictions are accurate. Research in this area focuses on adaptive control techniques, where the control policy dynamically adjusts based on the observed accuracy of predictions, and on novel mathematical frameworks for analyzing the tradeoffs between robustness and consistency in control performance given potentially untrustworthy ML models.

DISC Policy Design

#

The DISC policy design centers on effectively leveraging machine learning (ML) predictions while mitigating potential inaccuracies. A key innovation is the introduction of an online learning mechanism to dynamically adjust a confidence parameter, denoted as λ. This parameter reflects the trustworthiness of ML predictions for each latent variable contributing to system perturbations. DISC seamlessly integrates the strengths of both optimal control (when predictions are accurate) and robust control (when predictions are unreliable), achieving a desirable tradeoff between consistency and robustness. The algorithm’s design skillfully disentangles heterogeneous sources of disturbances, enabling more precise estimation of confidence and a better response to varying prediction quality. This ‘best of both worlds’ approach represents a significant advancement in handling uncertainties within online decision-making systems. The theoretical analysis provides rigorous competitive ratio bounds under both linear and general mixing scenarios, demonstrating provable improvements over methods without confidence parameter learning. This policy’s adaptability to real-world settings with changing dynamics is key to its practical significance.

Linear/General Mixing

#

The section exploring linear and general mixing scenarios within the context of handling untrusted ML predictions for control systems is crucial. Linear mixing simplifies the problem, assuming a direct linear relationship between latent variables and system disturbances. This allows for easier analysis and potentially tighter performance guarantees. However, real-world systems are rarely perfectly linear. General mixing, which allows for more complex, nonlinear relationships, is significantly more realistic. This increased complexity introduces challenges in terms of analysis and developing robust control strategies. The paper’s ability to provide competitive ratio bounds under both scenarios highlights the robustness of their proposed method. This is a key strength, demonstrating applicability to a wider range of practical situations beyond simplified linear models. The transition from the simpler linear case to the more challenging general case represents a substantial advancement, demonstrating the versatility and broader applicability of their approach in real-world scenarios where strict linearity is often an unrealistic assumption.

Real-World Case Studies

#

A dedicated section on real-world case studies would significantly strengthen this research paper. It would allow the authors to demonstrate the practical applicability and effectiveness of their proposed DISC policy. Two compelling examples are suggested: drone navigation under various weather conditions and voltage control in a power grid with heterogeneous power injections. For each case, the authors should present the experimental setup, including the specific challenges, the chosen parameters for the DISC policy, a comparison against established baseline methods, and a quantitative evaluation of the results. A detailed discussion on the results is essential, highlighting the advantages of DISC, particularly in terms of robustness and near-optimality. Visualizations, such as graphs or plots of trajectories and cost functions, would significantly enhance the clarity and impact of the analysis. The case studies should demonstrate that the proposed method works under real-world constraints and outperforms existing approaches in handling uncertainties and achieving near-optimal performance. By presenting such detailed and rigorous case studies, the authors will build credibility for their methodology and demonstrate its value beyond theoretical claims.

Future Research

#

Future research directions stemming from this disentanglement-focused LQR control work could explore several promising avenues. Extending the approach to nonlinear dynamical systems is a crucial next step, moving beyond the linear mixing assumption to handle more complex real-world scenarios. This would involve investigating robust online learning methods for non-convex optimization problems and developing tighter competitive ratio bounds. Another important area is adapting the framework to other online decision-making problems, such as online caching, online routing, and online resource allocation. Determining the universality of the ‘best-of-both-worlds’ competitive ratio bounds across diverse problem domains would provide significant theoretical insights. Finally, empirical evaluation on a wider range of real-world applications, coupled with a careful investigation of broader societal impacts is necessary. The application to autonomous driving, robotics, and energy grids opens exciting possibilities, but thorough ethical considerations are paramount. Investigating the impact of model bias and robustness against adversarial attacks is particularly crucial for trustworthy deployment.

More visual insights

#

More on figures

The figure illustrates the system model used in the paper. On the left, it shows a series of disentangled latent variable predictions generated by an untrusted machine learning (ML) agent at different time steps (t). On the right, it shows the observed mixed perturbations in the system, resulting from a combination of these latent variables. The system’s state is updated based on the current state, control actions, and these mixed perturbations. The figure highlights the challenge of using untrusted ML predictions in control problems.

This figure shows the results of a drone navigation experiment under windy and rainy conditions. The left panel shows the drone’s trajectory using the DISC policy compared to the optimal offline trajectory. The right panel shows a comparison of the cost ratios for DISC, LQR, MPC (with untrusted predictions), and a self-tuning policy across different levels of environmental unpredictability (controlled by the scaling factor ‘v’). The shadow area represents the standard deviation across five random trials.

This figure shows a diagram of a power grid with different types of power sources and loads. It also includes graphs showing the convergence of confidence parameters and temporal dynamics of latent time series for different power sources.

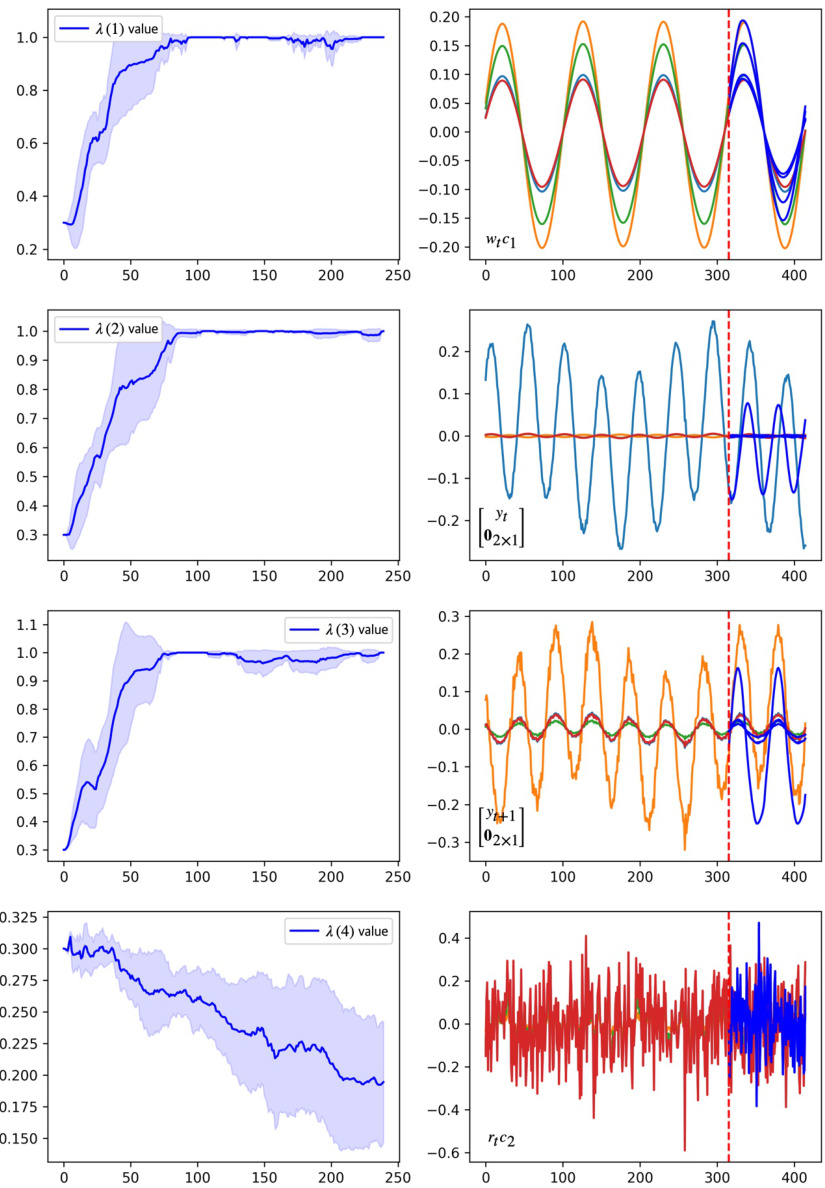
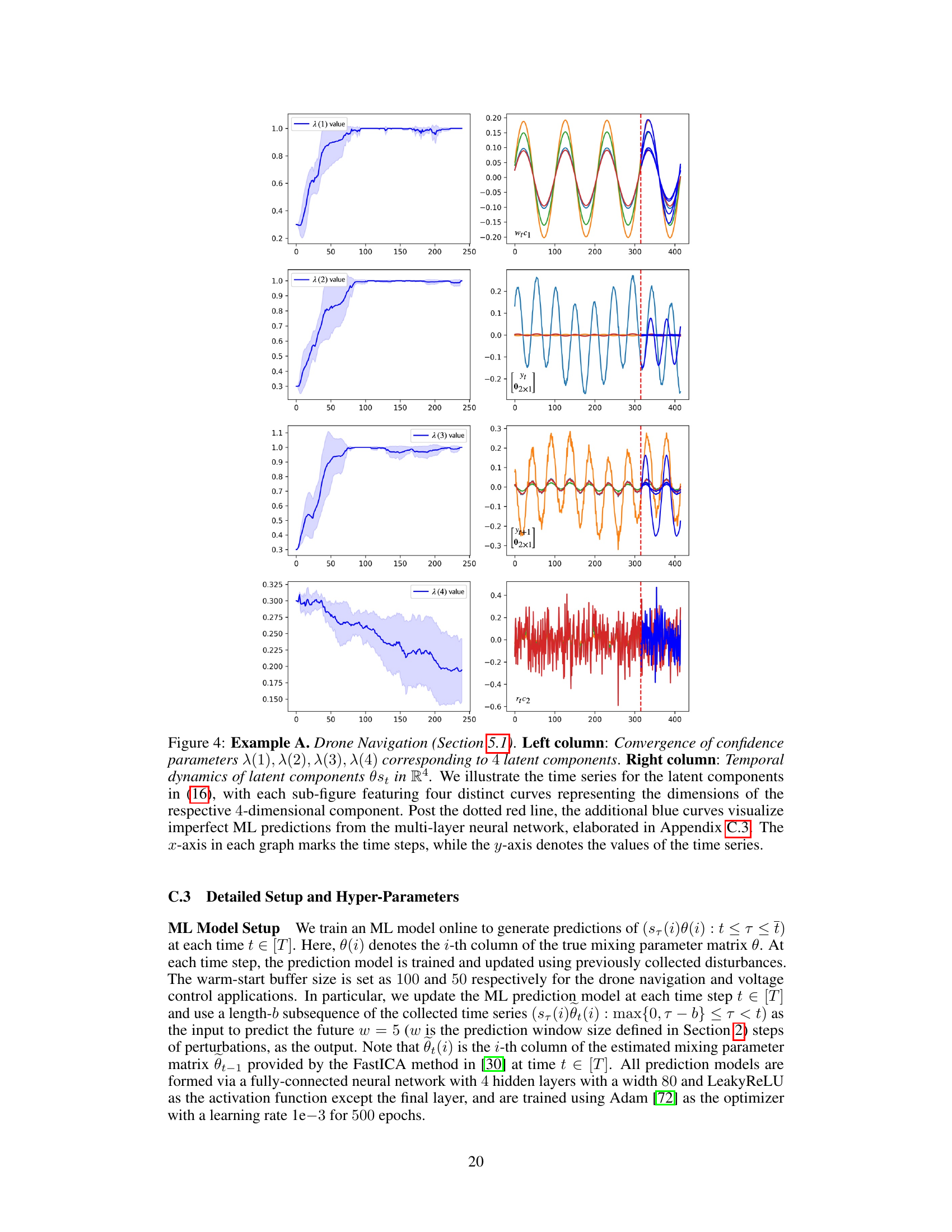
This figure shows the convergence of confidence parameters and the temporal dynamics of latent components for the drone navigation task. The left column displays the convergence of four confidence parameters (λ(1) to λ(4)), each associated with a latent component. The right column shows the time series for each of these four latent components. The dotted red line indicates a change in the data characteristics (a transition point). Blue curves after the dotted red line represent imperfect predictions from a neural network model.

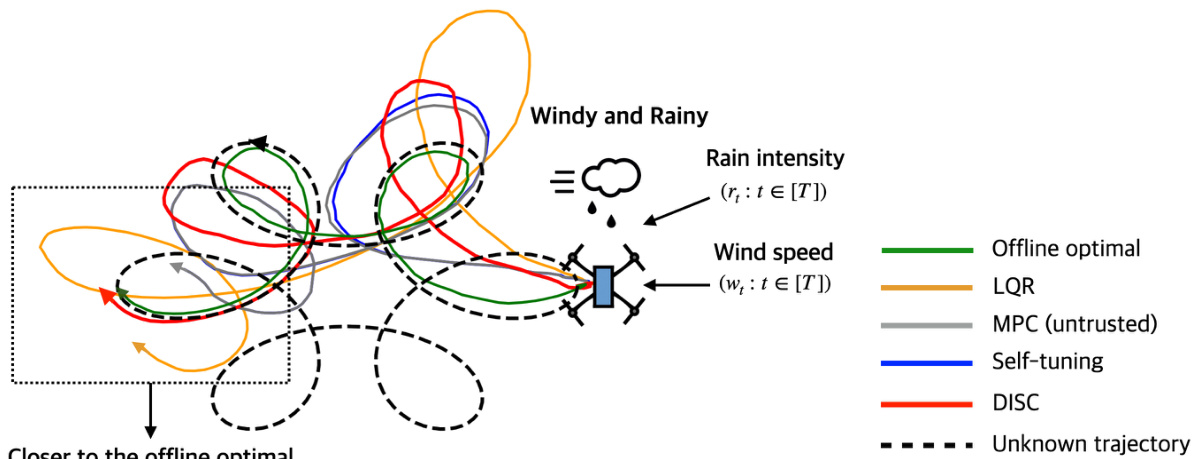
The figure shows the results of drone navigation experiments under windy and rainy conditions. The left panel illustrates the drone’s trajectory using different control policies, including the proposed DISC policy, compared to the optimal offline policy, LQR and an MPC policy using untrusted ML predictions. The right panel shows the cost ratios for the different policies with varying scaling factors, representing different levels of environmental uncertainty.

This bar chart compares the average total cost J(π) achieved by four different control policies: DISC, Self-tuning, MPC (untrusted), and LQR. The error bars represent the standard deviation across multiple runs. The LQR cost is shown as a dashed horizontal line for reference. DISC outperforms the other policies, suggesting its effectiveness in minimizing cost for voltage control in power grids.

This figure illustrates the system model used in the paper. The left side shows the disentangled latent variable predictions from an untrusted ML agent, while the right side depicts the observed mixed perturbations. The model shows how the untrusted ML agent’s predictions, the control policy, and the dynamical system interact to produce the observed states. The figure highlights the core components of the system and their relationships.

This figure illustrates the system model used in the paper. An untrusted machine learning agent provides predictions for disentangled latent variables, which are then combined with observed mixed perturbations to update the system state. The control policy uses these predictions and the observed state to determine actions. The figure shows the interaction between the ML agent, the dynamical system, and the control policy. The time series plots show the disentangled latent variable predictions and the mixed perturbations over time.

More on tables

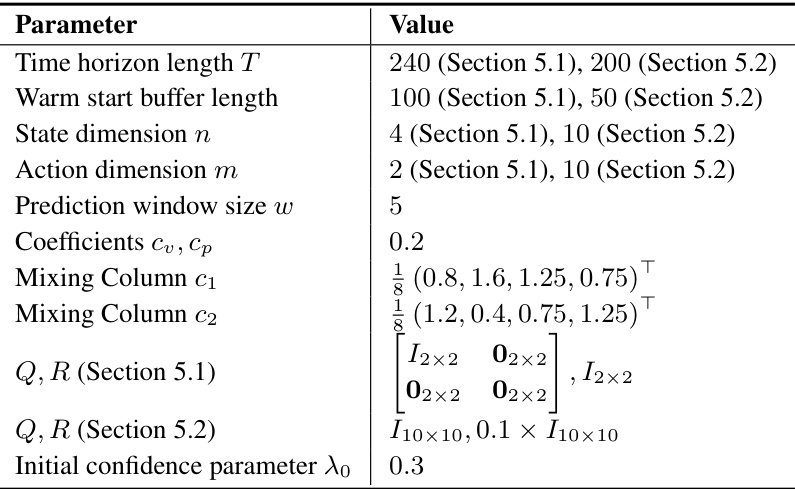
This table lists the values of various parameters and hyperparameters used in the experiments described in Section C of the paper. These parameters control aspects of the drone navigation and voltage control experiments, such as the time horizon, prediction window size, and neural network architecture. The table is divided into two parts: basic control problem setup and neural network hyperparameters.

This table summarizes the key assumptions made in several nonlinear ICA models, beyond the common assumptions that latent variables are mutually independent and at most one latent variable is Gaussian. The assumptions concern the mixing function and the latent variables and are crucial for identifiability in nonlinear ICA.

Full paper

#