↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Safe Reinforcement Learning (SRL) is crucial for deploying RL agents in safety-critical applications. Model Predictive Shielding (MPS), a popular SRL approach, uses a backup policy to ensure safety, but this often hinders progress. Existing MPS methods’ backup policies are conservative and task-oblivious, leading to high recovery regret and suboptimal performance.
This paper introduces Dynamic Model Predictive Shielding (DMPS) to overcome these limitations. DMPS employs a local planner to dynamically choose safe recovery actions that optimize both short-term progress and long-term rewards. The planner and neural policy work synergistically; the planner uses the neural policy’s Q-function to estimate long-term rewards, and the neural policy learns from the planner’s actions. DMPS guarantees safety during and after training, with theoretically proven bounded recovery regret. Experiments show DMPS significantly outperforms state-of-the-art methods in terms of both safety and reward.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in safe reinforcement learning. It addresses the limitations of existing methods by proposing DMPS, a novel approach that significantly improves safety and performance. This opens avenues for developing more robust and reliable safe RL agents for real-world applications, particularly in safety-critical domains like robotics and autonomous driving.
Visual Insights#

This figure shows the control flow of both MPS and DMPS. In MPS, if the learned policy suggests an action that would lead to an unsafe state, the backup policy is used. DMPS enhances this by using a local planner to find a better recovery action before resorting to the backup policy. The numbered steps highlight the differences: 1. Initial action from the learned policy; 2. Planner determines safe action; 3. The planner’s suggested safe action is used instead of the backup policy; 4. The backup policy is only used if the planner fails to find a safe and optimal plan.

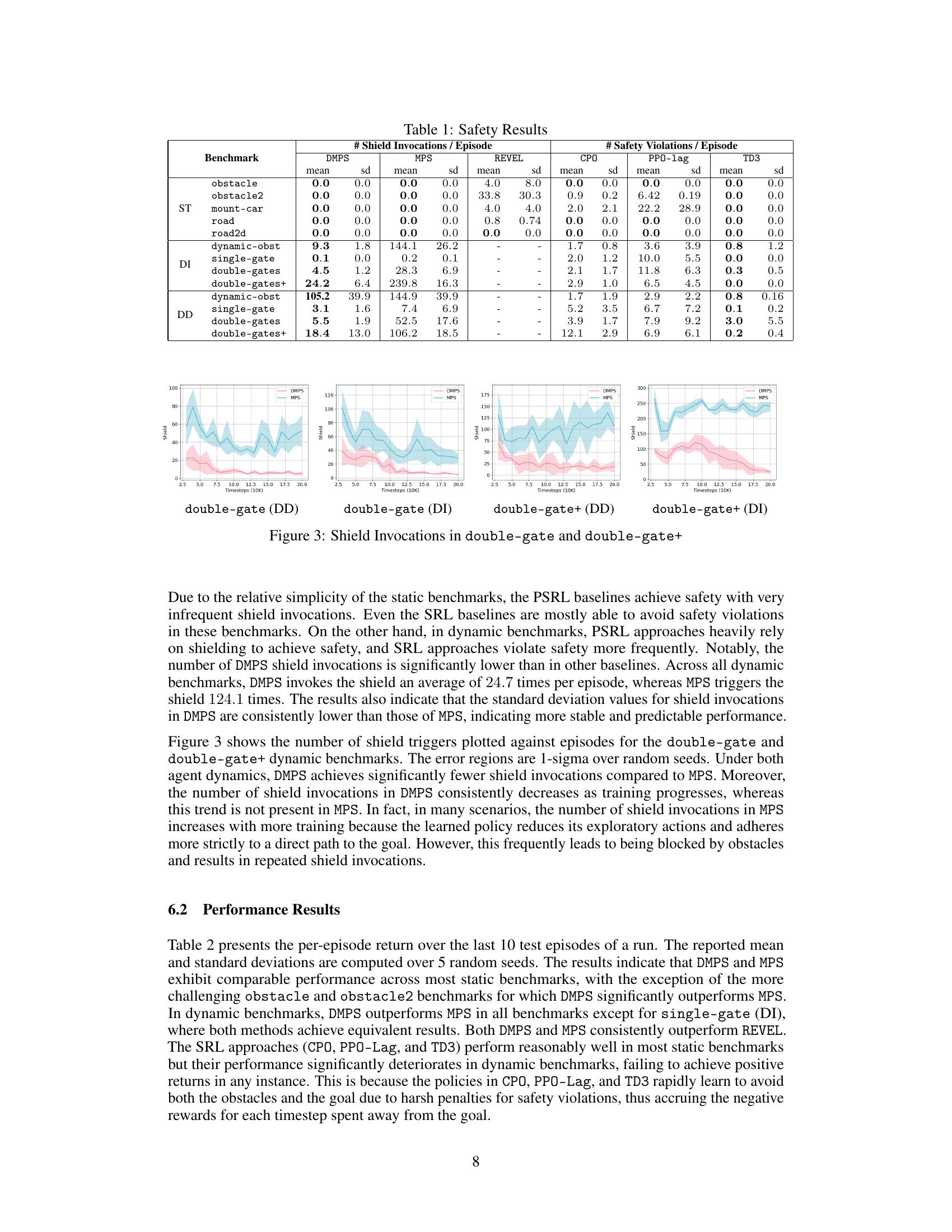
This table presents the safety performance of different reinforcement learning algorithms across various benchmark environments. For provably safe reinforcement learning (PSRL) methods like DMPS, MPS, and REVEL, the table shows the average number of times the safety shield was activated per episode, indicating how often the learned policy needed intervention to maintain safety. For statistically safe reinforcement learning (SRL) methods such as TD3, PPO-Lag, and CPO, the table presents the average number of safety violations per episode. A lower number of shield invocations or safety violations signifies better safety performance.
In-depth insights#
DMPS: A Novel SRL Approach#
DMPS presents a novel approach to provably safe reinforcement learning (SRL), addressing limitations of existing Model Predictive Shielding (MPS) methods. DMPS enhances MPS by incorporating a local planner to dynamically select safe recovery actions, optimizing both short-term progress and long-term rewards. This synergistic interplay between the planner and the neural policy is crucial. The planner leverages the neural policy’s Q-function to evaluate long-term rewards, extending its horizon beyond immediate safety. Conversely, the neural policy learns from the planner’s recovery actions, leading to high-performing and safe policies. DMPS guarantees safety during and after training, offering bounded recovery regret that decreases exponentially with planning horizon depth. Empirical results demonstrate that DMPS outperforms state-of-the-art baselines in terms of both reward and safety, showcasing its potential for real-world applications demanding provable safety guarantees.
Synergistic Policy-Planner Role#
The synergistic policy-planner relationship is a core element of the proposed Dynamic Model Predictive Shielding (DMPS) framework. The planner, acting as a local decision-maker, dynamically selects safe recovery actions, optimizing both short-term progress and long-term rewards by incorporating the learned neural policy’s Q-function. This integration allows the planner to look beyond its immediate planning horizon, making more informed decisions. Conversely, the neural policy benefits from the planner’s actions, learning to avoid unsafe states more efficiently by observing and adapting to the planner’s strategies. This iterative interaction creates a feedback loop that continuously improves both the safety and performance of the agent. This synergy fundamentally distinguishes DMPS from existing MPS methods, which rely on static, task-oblivious backup policies. The resulting policy not only guarantees safety but also converges towards higher rewards, representing a significant advance in provably safe reinforcement learning.
Provably Safe Guarantee#
Provably safe reinforcement learning (RL) aims to create agents that never violate safety constraints, a critical aspect for real-world applications. A provably safe guarantee in this context means that the algorithm mathematically proves the agent will remain within safety boundaries throughout training and deployment, not just probabilistically. This is achieved through various techniques, often involving formal verification methods or the use of safety mechanisms like shielding or control barrier functions. A key challenge is balancing safety with performance: overly conservative safety measures can severely limit the agent’s ability to achieve its primary goals. Therefore, effective provably safe methods must find a way to rigorously ensure safety while allowing for sufficient exploration and learning to achieve optimal performance. Formal guarantees are the cornerstone of this type of safety, providing a level of confidence unavailable in probabilistic approaches. However, creating these guarantees is mathematically complex and often computationally expensive, particularly in continuous high-dimensional state spaces. This complexity presents a tradeoff between strong safety assertions and feasibility. Future research should focus on developing more efficient and scalable techniques to provide provably safe guarantees for increasingly complex RL tasks.
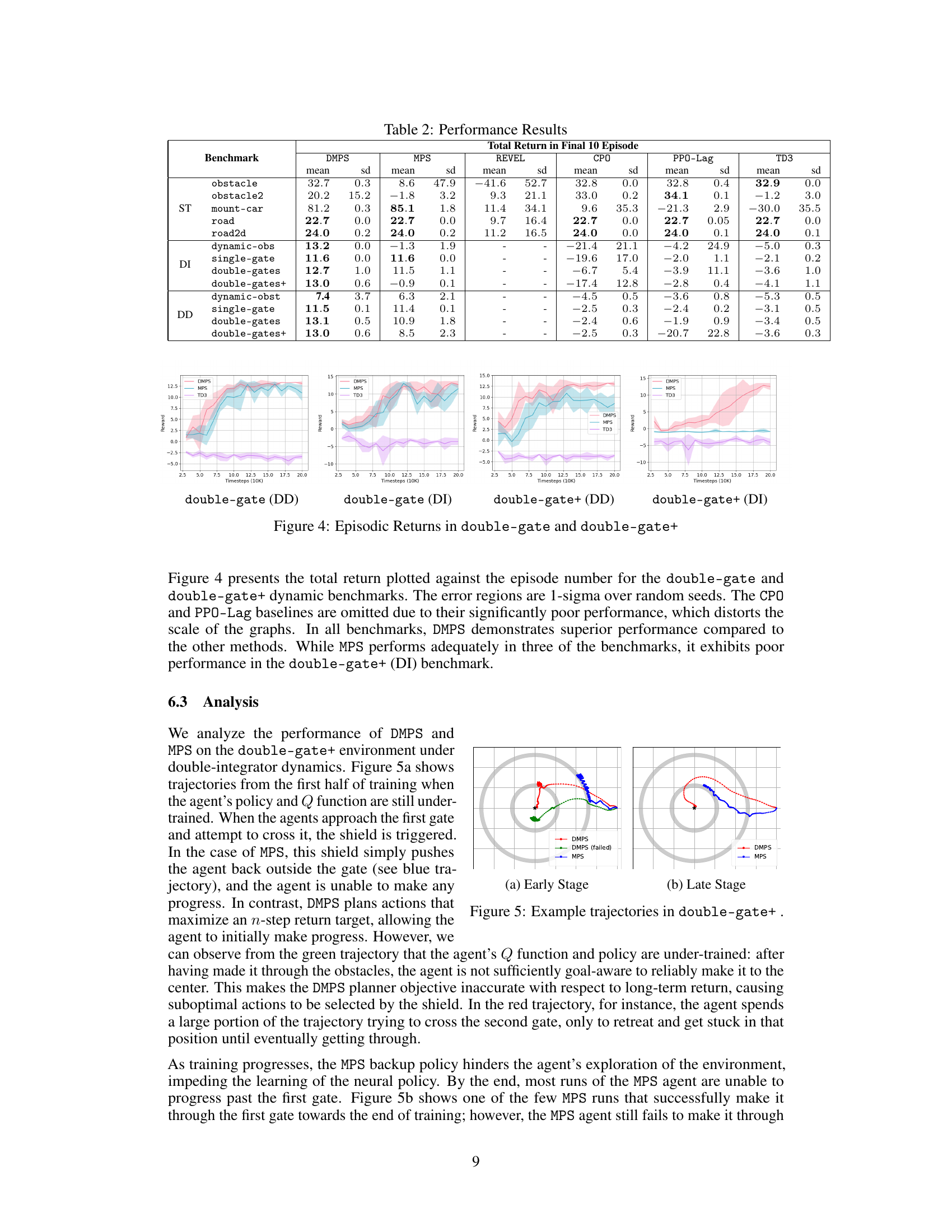
Empirical Evaluation#
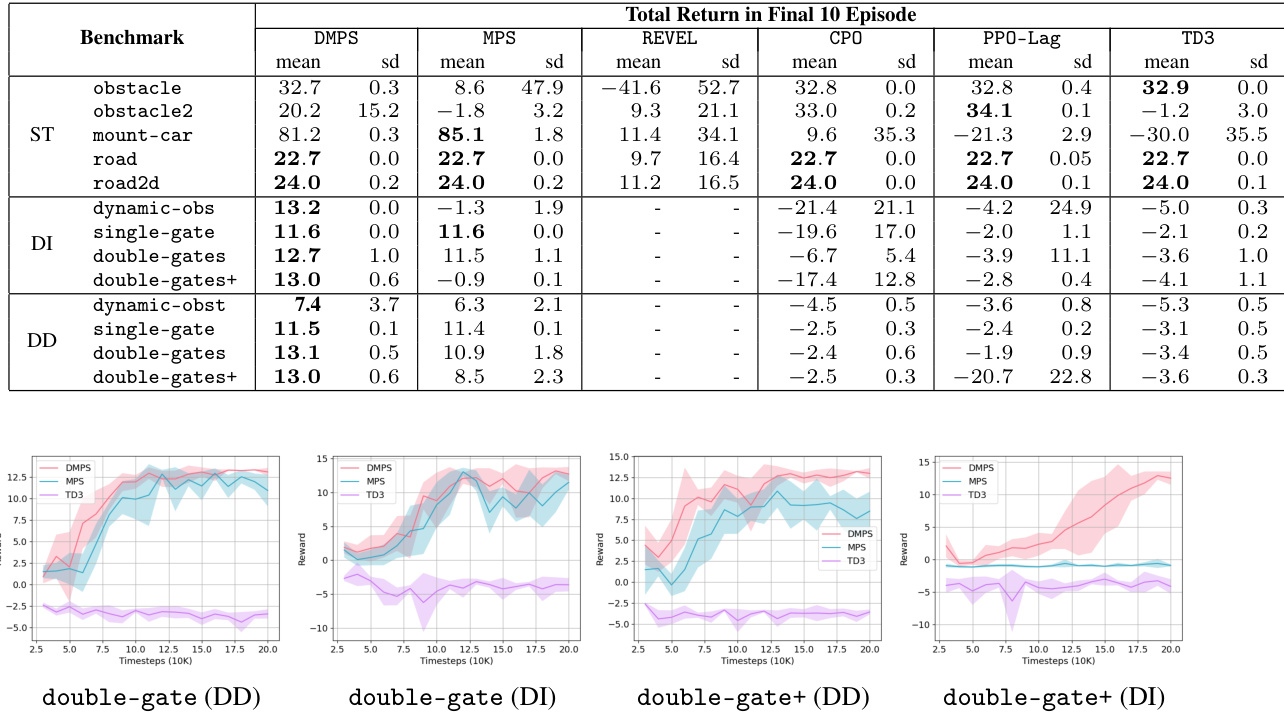
An empirical evaluation section in a research paper should rigorously assess the proposed method’s performance. It needs to clearly define the metrics used to measure success, selecting those relevant to the research question and the specific problem addressed. The evaluation should involve a sufficient number of experiments and datasets, diverse enough to demonstrate generalizability. Baselines for comparison are crucial; these should be established methods, chosen strategically to highlight the novelty and improvements made. The results should be presented clearly, perhaps with tables and graphs, and accompanied by statistical significance tests to rule out random chance as a major factor. Furthermore, a discussion of the results is necessary, analyzing strengths and weaknesses, and contextualizing the findings within existing literature. Finally, a well-executed empirical evaluation will transparently discuss limitations and suggest avenues for future work, thus enhancing the overall trustworthiness and impact of the research.
DMPS Limitations#
The Dynamic Model Predictive Shielding (DMPS) approach, while promising for provably safe reinforcement learning, presents some limitations. Determinism is a key constraint; DMPS relies on a perfect-information deterministic model, limiting real-world applicability where stochasticity is prevalent. The algorithm’s computational overhead, stemming from the use of a local planner, poses a significant challenge, especially as the planning horizon deepens, potentially causing exponential growth in computation. While the planning horizon can mitigate this, there’s a trade-off with optimality. Additionally, the method’s success depends on the sufficiency of the planning horizon. A short horizon may not provide adequate foresight to address complex situations, resulting in suboptimal recovery plans. Finally, the approach’s effectiveness rests on the accurate modeling of the environment’s dynamics, and deviation from this ideal could compromise the safety guarantees.
More visual insights#
More on figures

This figure shows four different trajectories for an agent trying to reach a goal while avoiding static obstacles. (a) shows an unsafe trajectory where the agent collides with an obstacle. (b) shows a safe trajectory generated by MPS, but it is suboptimal because the agent halts instead of finding a better path around the obstacle. (c) shows an optimal and safe trajectory, which is what DMPS aims to achieve. (d) illustrates the planning phase of DMPS, where the planner searches for a safe and optimal path to reach the goal.

This figure shows example trajectories of DMPS and MPS agents in the double-gate+ environment. Panel (a) displays trajectories during early training, illustrating that DMPS (green) navigates more effectively through the gates than MPS (blue). A failed DMPS attempt (red) is also shown. Panel (b) shows trajectories in a later stage of training, demonstrating that while DMPS can successfully navigate the obstacles, MPS still struggles to pass through even one gate.
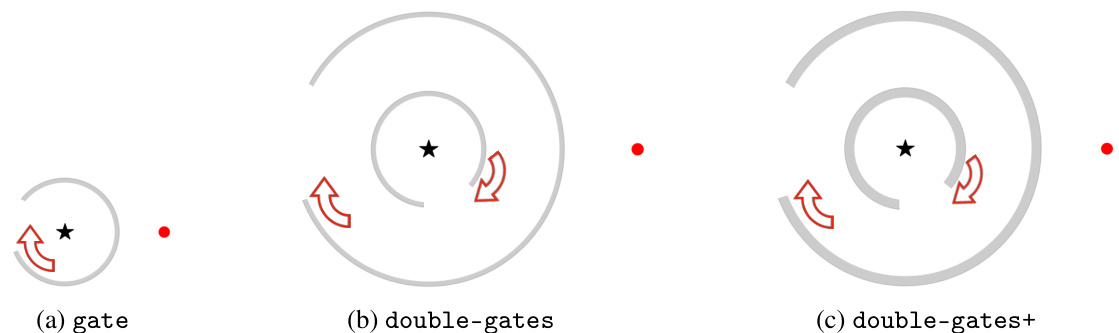
This figure visualizes three dynamic environments used in the experiments: single-gate, double-gates, and double-gates+. Each environment features a goal (black star) and an agent (red circle) that must navigate through one or more concentric rotating walls to reach the goal. The direction of rotation for the walls is indicated by red arrows. The environments increase in complexity, starting with a single rotating wall (single-gate), then two concentric walls (double-gates), and finally two concentric walls with increased thickness (double-gates+), making navigation more challenging.
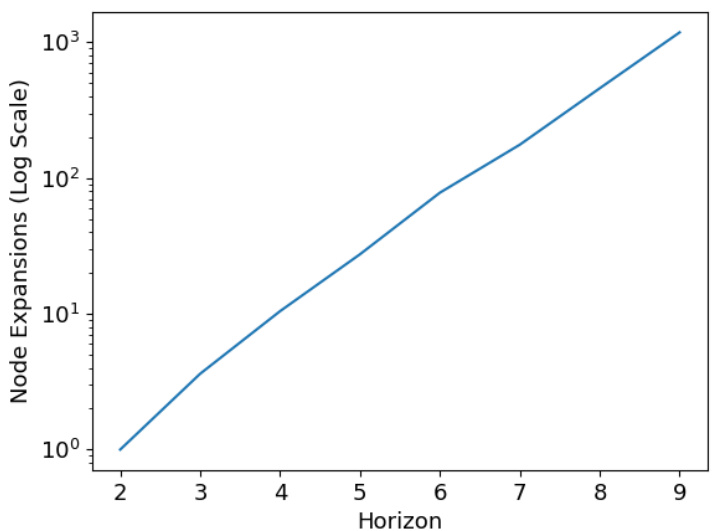
This figure shows how the computation time required for planning scales with the planning horizon. It plots the number of node expansions performed by the MCTS planner (y-axis, log scale) against the planning horizon (x-axis). The exponential relationship demonstrates the increased computational cost of planning as the lookahead increases.
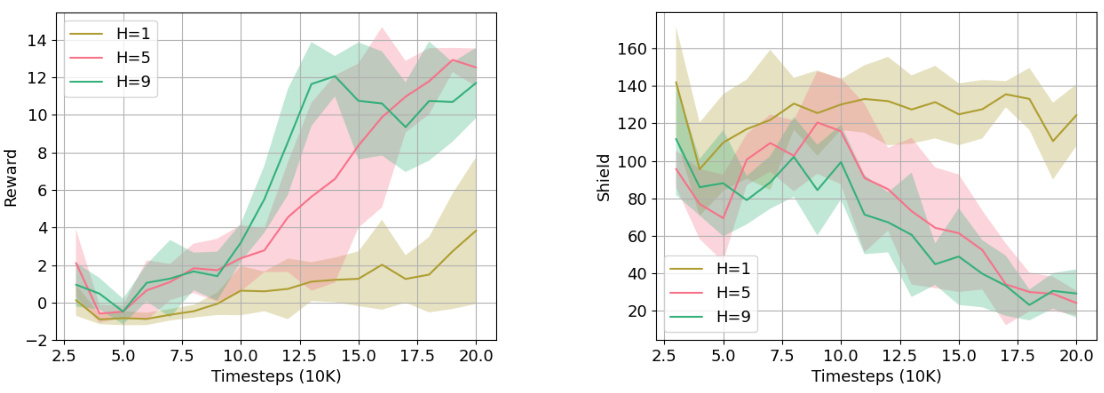
The plots show the episodic return and number of shield invocations over time for the double-gates+ environment (double integrator dynamics) when using planning horizons of 1, 5, and 9. The shaded regions represent the standard deviation over five random seeds. The results indicate that longer planning horizons lead to better performance, achieving higher rewards and fewer shield invocations. However, there is a diminishing return in performance as the horizon length increases, suggesting a trade-off between the benefits of long-horizon planning and the associated computational cost.
More on tables
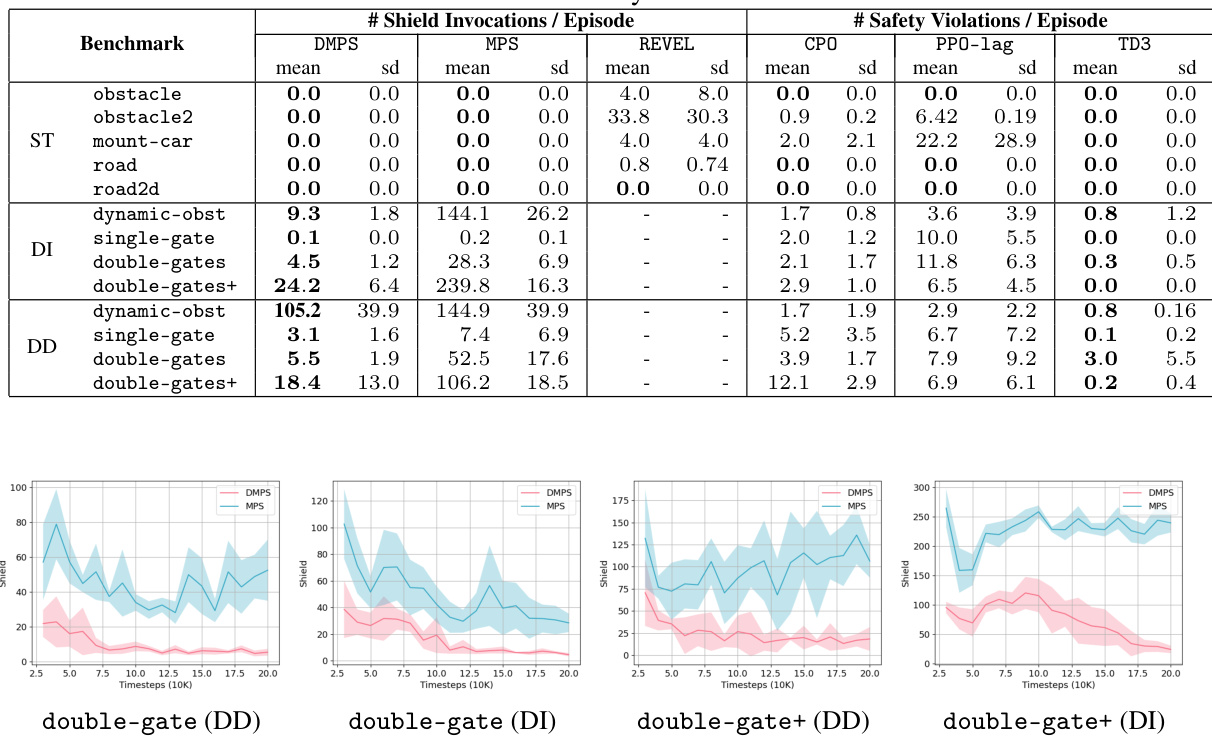
This table presents the results of safety experiments conducted across various benchmarks. For provably safe reinforcement learning (PSRL) methods (DMPS, MPS, and REVEL), which guarantee worst-case safety, the average number of shield invocations per episode is reported. Fewer shield invocations indicate better performance. For statistically safe reinforcement learning (SRL) methods (TD3, PPO-Lag, and CPO), which aim to reduce safety violations, the average number of safety violations per episode is reported. Lower numbers of violations represent better safety performance. The results are averaged over five independent random seeds. Standard deviations are also provided.
This table presents the safety performance results of different reinforcement learning algorithms. For provably safe reinforcement learning (PSRL) methods, it shows the average number of shield invocations per episode, indicating how often the safety mechanism intervened. Lower numbers suggest better safety performance. For statistically safe reinforcement learning (SRL) methods, it presents the average number of safety violations per episode, with higher numbers indicating poorer safety performance. The results are categorized by benchmark environment (static or dynamic) and agent dynamics (differential drive or double integrator).

This table presents a comparison of safety performance metrics across different reinforcement learning algorithms on various benchmark tasks. For provably safe reinforcement learning (PSRL) methods, the average number of shield invocations per episode is reported. For statistically safe reinforcement learning (SRL) methods, the average number of safety violations per episode is shown. Lower numbers in both columns indicate better safety performance.
Full paper#