Unsupervised Object Detection with Theoretical Guarantees

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial because it bridges the gap between theoretical guarantees and practical unsupervised object detection. It provides a novel method with provable theoretical bounds on its error, unlike existing methods that rely solely on empirical evidence. This opens up new research avenues for developing reliable and trustworthy object detection systems. The methodology has potential applications in sensitive areas such as medical image analysis and autonomous driving, where reliable performance is paramount.

Visual Insights

#

This figure illustrates the architecture of the proposed unsupervised object detection method. The encoder uses a CNN (ψ) to process the input image (x) and generate embedding maps (e₁, …, en). A soft argmax function then extracts latent variables (z₁,x, z₁,y, …, zn,x, zn,y) representing object positions. The decoder takes these latent variables, renders Gaussians (ê₁, …, ên) at those positions, combines them with positional encodings, and uses another CNN (φ) to reconstruct the predicted image (î). The reconstruction loss L(î, x) is used for training.

In-depth insights

#

Unsupervised Object Detection

#

Unsupervised object detection presents a significant challenge in computer vision, as it aims to identify and locate objects within images without relying on labeled training data. This contrasts with supervised methods that require extensive human annotation. The absence of labeled data necessitates innovative approaches to learn object representations and their spatial locations. A key aspect of this problem involves the design of robust and reliable algorithms that can generalize well to unseen data. Theoretical guarantees, as explored in some research, can offer increased confidence in the accuracy and reliability of such methods, particularly in safety-critical applications. The exploration of novel architectures and training techniques is crucial to overcome the challenges posed by the lack of supervision and achieving a level of performance comparable to or exceeding that of supervised counterparts. The field is also actively investigating the use of self-supervision or weak supervision to leverage existing image data more efficiently and improve model generalization. Ultimately, advancements in unsupervised object detection are likely to have a significant impact on various applications, including robotics, autonomous driving, and medical image analysis.

Theoretical Guarantees

#

The concept of ‘Theoretical Guarantees’ in the context of unsupervised object detection is a significant contribution. It signifies a departure from purely empirical approaches, offering mathematical proof about the accuracy of the model’s predictions. Instead of relying solely on experimental results, which can be dataset-specific, the presence of theoretical guarantees provides a stronger foundation for trust in the model’s performance. This is particularly crucial in unsupervised learning, where ground truth is unavailable for training. The guarantees, likely expressed in terms of bounds on the error, suggest a level of predictability in how well the system will detect objects under different conditions. However, it’s vital to carefully examine the assumptions and limitations behind these theoretical guarantees. The real-world applicability of the method depends on how well these assumptions reflect the characteristics of real-world data. Therefore, while theoretical guarantees improve confidence and reliability, it’s essential to consider the practical scope of these guarantees. The successful validation of theoretical predictions through experimental results offers further reassurance, strengthening the credibility of the proposed approach.

Equivariant Autoencoder

#

An equivariant autoencoder is a neural network architecture designed to learn representations that are invariant or covariant to specific transformations of the input data. Unlike standard autoencoders, which typically learn features sensitive to the exact position or orientation of objects, an equivariant autoencoder explicitly incorporates the transformation’s effects into its design. This often involves using layers like convolutional or other group-equivariant layers that maintain specific relationships between input and output features under the given transformations. The key advantage is that the learned latent representations are more robust to variations in the input, leading to improved generalization and robustness in downstream tasks like object recognition or classification. By explicitly enforcing equivariance, the model can learn more meaningful and interpretable features, reducing overfitting and enhancing transferability across different datasets or views of the same object. This approach is particularly beneficial for applications in computer vision where dealing with variations in viewpoint, scale, or other transformations is common. A limitation might be the increased complexity in design and training compared to standard autoencoders, potentially necessitating more sophisticated optimization techniques.

Position Error Bounds

#

Analyzing potential position errors is critical in object detection. Error bounds, which define the maximum deviation between predicted and actual object locations, are essential for evaluating algorithm reliability. A tight error bound suggests high accuracy and trustworthiness. Factors influencing error bounds include encoder and decoder receptive field sizes, object size, and Gaussian width used in rendering. Larger receptive fields tend to increase error, while smaller objects might have smaller errors. The Gaussian width impacts the smoothness of the rendering and the tolerance for positional shifts. Theoretically proving these bounds provides a strong guarantee of performance, especially useful for safety-critical applications where confidence in prediction accuracy is paramount. Experimental validation against theoretical bounds demonstrates the method’s effectiveness and precision. The study of position error bounds offers a systematic way to quantify and improve object detection methods.

Future Research

#

Future research directions stemming from this work could explore several promising avenues. Extending the theoretical framework to handle more complex scene configurations, such as occlusions and varying illumination conditions, would significantly enhance the robustness of unsupervised object detection. Investigating different network architectures, beyond the CNN-based autoencoder, such as transformers or graph neural networks, could potentially improve accuracy and efficiency. Developing methods for handling multiple object classes without supervision would be a major advancement, enabling a wider range of applications. Furthermore, in-depth analysis of the impact of different rendering techniques, such as varying Gaussian widths or incorporating more realistic object models, could reveal further insights into the method’s performance. Finally, applying the theoretical guarantees to real-world scenarios through extensive empirical evaluation on diverse datasets is crucial for establishing the practical viability of this approach and identifying potential limitations.

More visual insights

#

More on figures

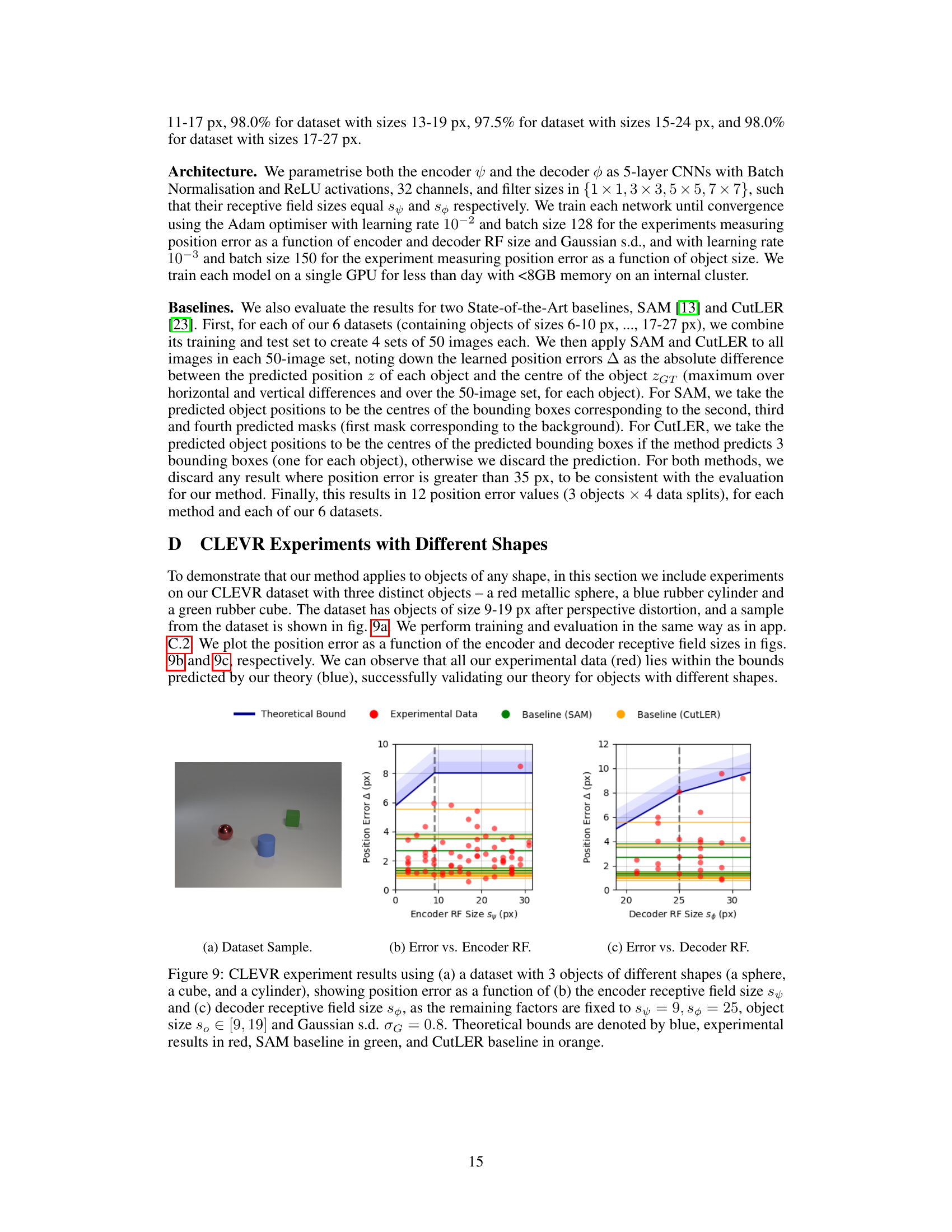
This figure illustrates the maximum position errors that can occur during the encoding and decoding processes. (a) shows the maximum error introduced by the encoder, which happens when the object and the encoder’s receptive field are positioned such that they overlap minimally. (b) illustrates the maximum error introduced by the decoder, which occurs when a portion of the Gaussian used to represent the object in the latent space lies within the decoder’s receptive field but is maximally distant from the object’s center.

This figure shows the maximum possible error in object position estimation due to the limitations of the encoder and decoder. (a) illustrates the error from the encoder, showing that the maximum error occurs when the receptive field is only partially overlapping with the object, resulting in an error proportional to the sum of half the receptive field and half the object size. (b) illustrates the error from the decoder, showing that it depends on the receptive field size, object size, and the Gaussian rendering variance. The maximum error occurs when the rendered Gaussian is at the edge of the decoder’s receptive field, but the center of the object is far from the Gaussian’s center.

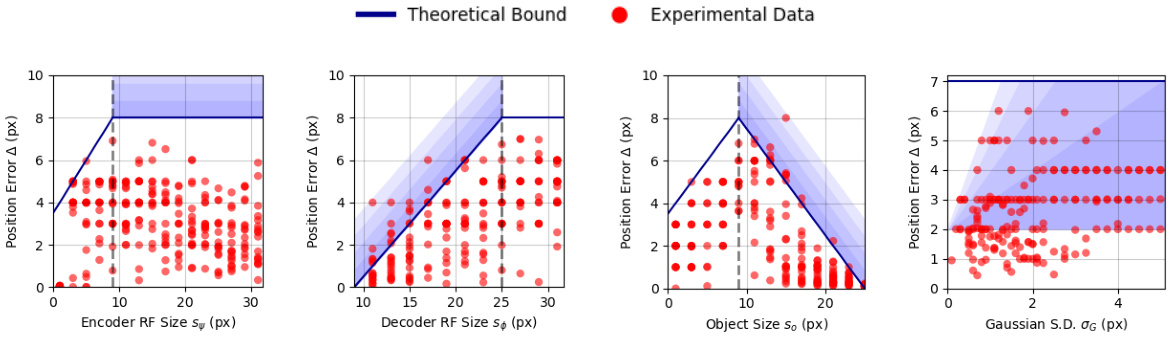
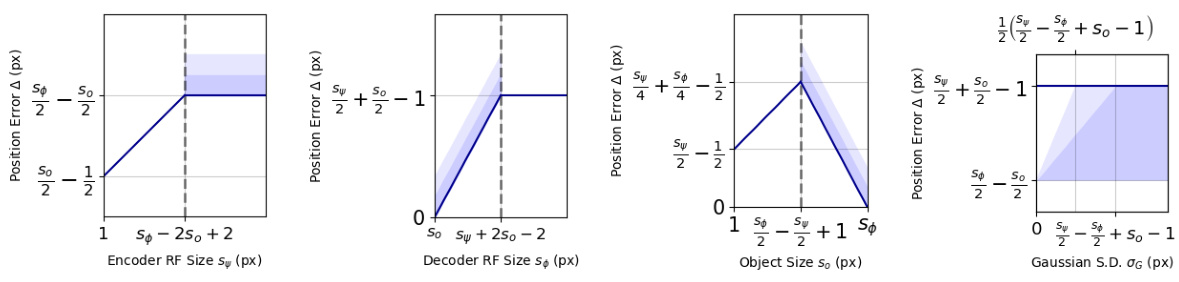
This figure shows the results of synthetic experiments validating the theoretical bounds on position error derived in the paper. It demonstrates the maximum position error as a function of four key variables: the encoder receptive field size, the decoder receptive field size, object size, and the standard deviation of the Gaussian used in the rendering process. Each subplot shows the relationship between the theoretical bound (blue line) and the experimental data (red dots) for one of the four variables. The shaded blue regions represent the probabilistic bound within one to four standard deviations of the mean.

This figure presents the results of synthetic experiments validating the theoretical bounds derived in the paper. It shows how the maximum position error of the object detection method varies as a function of four key parameters: encoder receptive field size, decoder receptive field size, object size, and Gaussian standard deviation. Each subplot displays the theoretical bound (blue line with shaded regions representing standard deviations) and the experimentally observed position errors (red dots). The consistency between theoretical predictions and experimental results supports the validity of the proposed method.

This figure displays the percentage of position errors that fall within two standard deviations of the theoretical bound, categorized by object size and method (Ours, CutLER, SAM). The plot visually represents the data presented in the accompanying table (6b), showing the percentage of errors within the theoretical bounds for different object sizes (9, 12, 15, 18, 21, 24 pixels). It highlights the consistent high accuracy of the proposed method in contrast to the other two methods, with the proposed method achieving 100% accuracy across all object sizes.

This figure presents the results of synthetic experiments validating the theoretical bounds derived in the paper. It shows the position error as a function of four key variables: encoder receptive field size, decoder receptive field size, object size, and Gaussian standard deviation. Each subplot displays the experimental data points (red dots) compared to the theoretical bounds (blue line, with shaded regions representing various standard deviations of the probabilistic bound for the decoder error). The results demonstrate a strong agreement between the theoretical predictions and the experimental findings, validating the accuracy of the theoretical analysis.

This figure illustrates the maximum position errors that can arise during the encoding and decoding processes in the proposed unsupervised object detection method. (a) shows the maximum error introduced by the encoder, which occurs when the encoder and object are maximally separated while still overlapping. (b) shows the maximum error introduced by the decoder, which occurs when a portion of the Gaussian used for rendering is within the decoder’s receptive field but maximally distant from the rendered object.

This figure shows the architecture of the proposed unsupervised object detection method. The encoder consists of a convolutional neural network (CNN) followed by a soft argmax function to extract object positions. The decoder consists of a Gaussian rendering function followed by another CNN to reconstruct an image. The latent variables represent the object positions.

This figure shows the results of synthetic experiments to validate the theoretical bounds derived in the paper. Each subfigure presents the position error plotted against one of the four variables (encoder receptive field, decoder receptive field, object size, and Gaussian standard deviation), while holding the others constant. The blue line represents the theoretical upper bound on the position error, with shaded areas indicating varying levels of uncertainty. Red dots show the experimentally observed position errors. The close correspondence between the experimental results and theoretical bounds supports the paper’s claims.

This figure illustrates the architecture of the unsupervised object detection method proposed in the paper. The encoder consists of a CNN followed by a soft argmax function to extract object positions, which are represented as latent variables. The decoder consists of a Gaussian rendering function followed by another CNN to reconstruct the image. The latent variables, representing the object positions, are used to render Gaussian maps at the corresponding positions. These maps, along with positional encodings, are then passed through a CNN to generate the predicted image. Finally, a reconstruction loss is computed between the original image and the predicted image.

This figure illustrates the architecture of the proposed unsupervised object detection method. The encoder uses a CNN to process an input image and extract embedding maps. A soft argmax function then identifies the peak locations within these maps, representing the latent variables (object positions). The decoder takes these latent variables, renders Gaussian functions at those locations, and uses another CNN to reconstruct the image from these rendered Gaussians and positional encodings. The reconstruction loss is calculated between the input and reconstructed images for training.

Full paper

#