↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
High-energy physics relies heavily on machine learning for extracting scientific understanding from complex experimental data. However, existing machine learning methods often struggle with the high dimensionality and specific symmetries of such data, hindering precision and data efficiency. The limitations of off-the-shelf architectures highlight the need for specialized methods that incorporate the underlying physical symmetries to improve results.
This research paper introduces the Lorentz Geometric Algebra Transformer (L-GATr), a novel architecture designed specifically for high-energy physics problems. L-GATr leverages geometric algebra to represent the data, incorporating the inherent Lorentz symmetry of relativistic kinematics. It combines this with a Transformer architecture to ensure versatility and scalability. The effectiveness of L-GATr is demonstrated through three distinct particle physics tasks: a regression problem using QFT amplitudes, a classification problem for top quark tagging, and a generative modeling task for reconstructing particles. L-GATr either matches or surpasses the performance of various existing state-of-the-art models in all three applications.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces a novel and highly efficient architecture for high-energy physics, addressing the need for better data efficiency and precision in complex machine learning problems. Its Lorentz-equivariant generative model is especially significant, opening new avenues for data generation and analysis in the field. The work’s general-purpose nature and scalability to large systems will be highly valuable to researchers, prompting further research into geometric deep learning and its applications.
Visual Insights#

This figure shows a schematic of the data analysis workflow in high-energy physics. It illustrates the process from initial particle interactions to final discoveries and measurements, highlighting the role of simulation and theory predictions. The three applications of the Lorentz Geometric Algebra Transformer (L-GATr) discussed in the paper are shown in orange, illustrating where they fit within the broader pipeline.
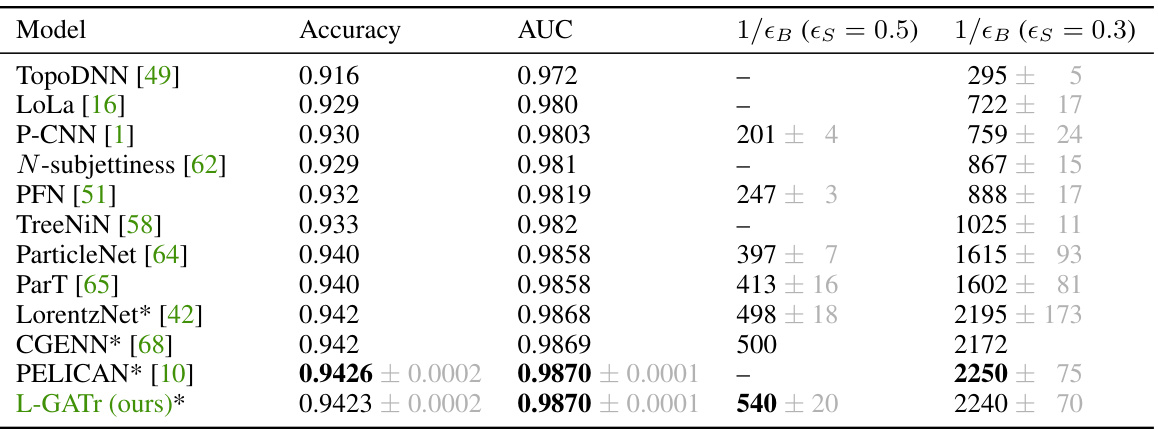
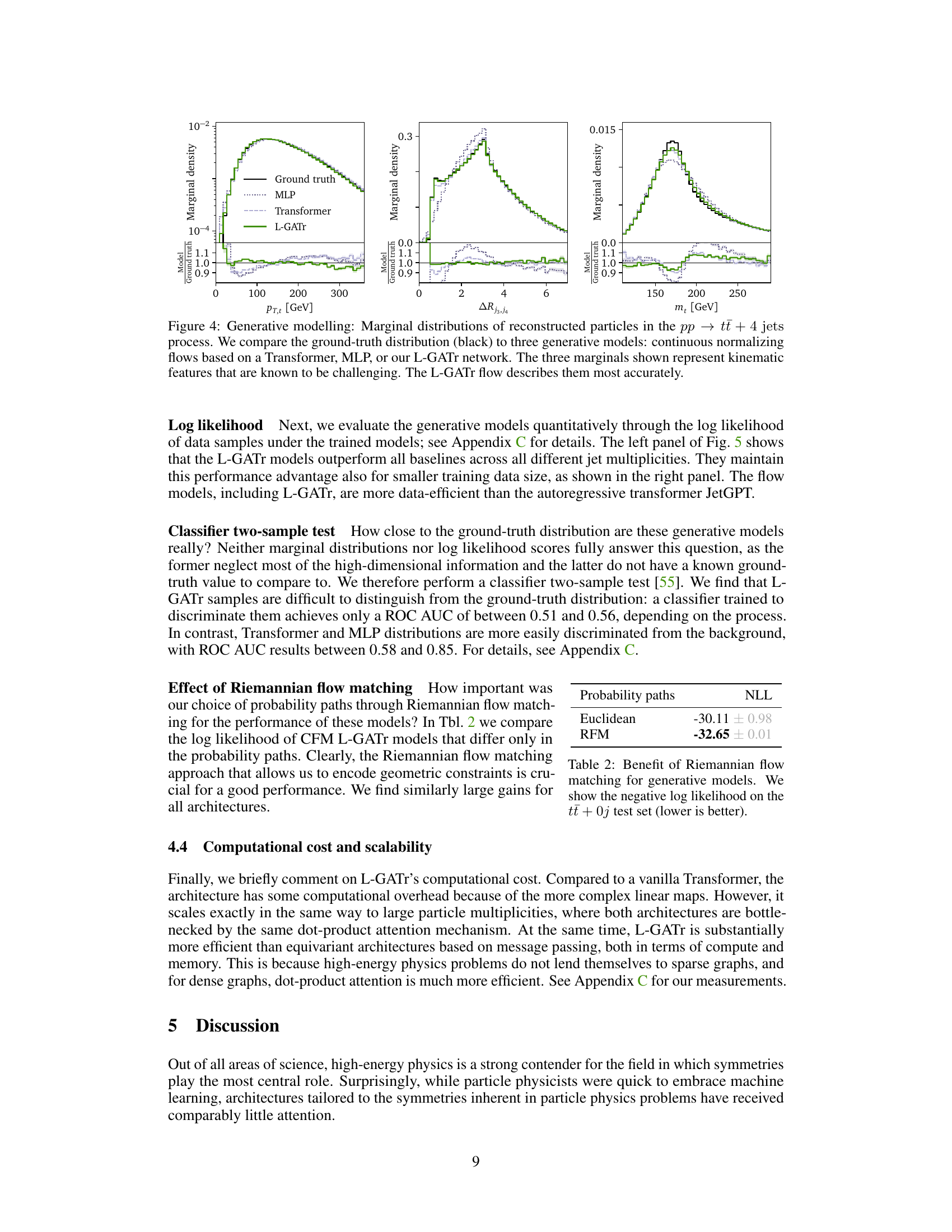
This table presents a comparison of different machine learning models for the task of top tagging. The table shows the accuracy, AUC (Area Under the ROC Curve), and inverse background acceptance rate (1/єB) for each model. Two different signal acceptance rates (єs = 0.5 and єs = 0.3) are considered. The best performing model for each metric is highlighted in bold. The results for the L-GATr model are averaged over five different random seeds to show the standard deviation.
In-depth insights#
Lorentz Symmetry#
Lorentz symmetry, a fundamental principle in special relativity, postulates that the laws of physics remain unchanged under Lorentz transformations. This symmetry is crucial in high-energy physics as it governs the behavior of particles at relativistic speeds. The paper leverages this symmetry by employing a Lorentz-equivariant architecture, ensuring that the model’s predictions transform consistently under Lorentz transformations. This equivariance offers significant advantages, reducing the amount of data needed for training and improving generalization to unseen scenarios. By incorporating Lorentz symmetry directly into the model’s design, the risk of the model learning incorrect or non-physical behaviors is reduced, leading to more accurate and efficient predictions The implications extend to generative modeling, where respecting Lorentz symmetry aids in creating realistic and physically plausible simulations of particle interactions.
Geometric Algebra#
Geometric algebra, within the context of this research paper, serves as a powerful mathematical framework for representing and manipulating high-dimensional data, particularly relevant in high-energy physics. Its core strength lies in its ability to encode geometric information intrinsically, moving beyond traditional vector representations. This is crucial because particle interactions are inherently geometric, governed by symmetries like Lorentz transformations. The paper leverages geometric algebra to build Lorentz-equivariant neural networks, ensuring that the network’s output transforms consistently with the input under Lorentz transformations. This approach offers significant advantages by incorporating physical symmetries directly into the network architecture, leading to improved data efficiency and potentially superior predictive accuracy. The use of geometric algebra is not merely a computational trick; it’s a fundamental shift in how the data’s intrinsic structure is utilized for effective learning, resulting in a more powerful and physically meaningful model.
Transformer Networks#
Transformer networks have revolutionized various fields, demonstrating significant advantages in handling sequential data. Their ability to process information in parallel, unlike recurrent networks, allows for faster training and improved performance on long sequences. The core mechanism, self-attention, enables the network to weigh the importance of different parts of the input when generating an output, capturing intricate relationships within the data. However, the quadratic complexity of self-attention with respect to sequence length presents a scalability challenge for very long sequences. Ongoing research focuses on improving efficiency, including techniques like sparse attention and linearized attention, to address this limitation and enable the application of transformers to even more extensive datasets. The versatility of transformer architecture is further highlighted by its adaptability to various tasks beyond sequence modeling, including image recognition, natural language processing, and time-series analysis, showcasing its potential as a general-purpose deep learning framework.
Generative Modeling#
The research explores generative modeling in high-energy physics, aiming to bypass computationally expensive simulations. Lorentz-equivariant flow matching, a novel technique leveraging the symmetry properties of particle physics, is introduced. This approach utilizes a continuous normalizing flow based on the L-GATr architecture, trained using Riemannian flow matching. This methodology offers advantages such as scalability and the ability to handle sharp edges and long tails in high-dimensional data distributions. By using physically motivated coordinates in the flow, it ensures adherence to physical constraints, significantly improving the model’s efficiency and the quality of the generated samples. The results show promising performance, demonstrating the potential of the approach for enhancing the efficiency of high-energy physics data analysis.
High-Energy Physics#
High-energy physics (HEP) grapples with the fundamental constituents of matter and their interactions at incredibly high energies. The Large Hadron Collider (LHC), a monumental machine, exemplifies this pursuit, colliding protons at near light speed to generate data at a rate of 10^15 bytes per second. This massive dataset requires advanced filtering and processing. Machine learning (ML) has emerged as a critical tool in HEP, accelerating various stages of analysis. This includes filtering raw data, identifying patterns indicative of new particles, and creating theoretical models to predict experimental outcomes. However, traditional ML methods struggle with HEP data’s unique characteristics, such as high dimensionality and inherent symmetries. Lorentz invariance, a fundamental principle of relativity, presents an opportunity and a challenge. The paper explores how creating models that respect this symmetry can improve accuracy and efficiency in HEP data analysis, thus leading to breakthroughs in understanding fundamental physics.
More visual insights#
More on figures
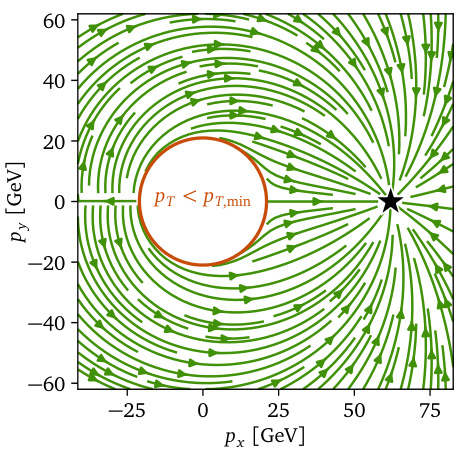
This figure shows the target vector field used in Riemannian flow matching for training the generative model. The green lines represent probability paths from a base distribution to the target data distribution. The red circle highlights a phase-space boundary (pT < pT,min); the model is designed to respect this boundary, ensuring generated particles are physically realistic.

This figure shows the performance of L-GATr and other methods on the task of creating surrogate models for quantum field theory amplitudes. The left panel compares the mean squared error (MSE) of different methods for processes with increasing numbers of particles. L-GATr consistently outperforms other models, especially for more complex processes. The right panel shows how the MSE changes as the size of the training dataset is varied, demonstrating that L-GATr is data efficient.
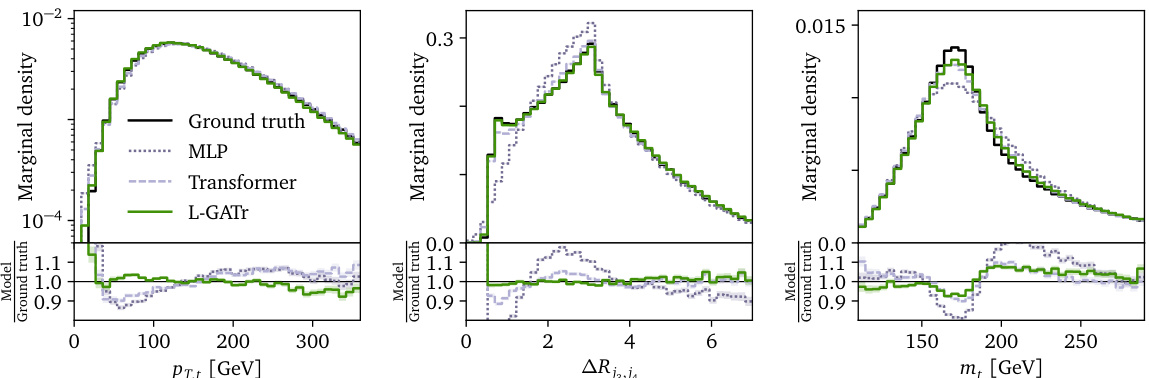
This figure compares the marginal distributions of reconstructed particles from ground truth data and three different generative models: a continuous normalizing flow based on a Transformer, an MLP, and the proposed L-GATr network. The three marginals shown (pT,j, ΔRj,j, mt) represent challenging kinematic features often difficult for generative models to capture accurately. The figure demonstrates that the L-GATr generative model produces distributions that closely match the ground truth.

This figure compares the performance of different generative models, including L-GATr, in terms of negative log-likelihood on a test dataset. The left panel shows the performance across different processes (varying jet multiplicities), while the right panel shows how the performance changes as the amount of training data increases. Error bars represent the standard deviation over three different random seeds. L-GATr consistently outperforms other models, demonstrating its effectiveness in generative modeling of particle physics data.

This figure presents the results of a classifier two-sample test, evaluating the quality of samples generated by various generative models. The left panel shows the performance for different processes (varying jet multiplicities), while the right panel shows performance as a function of the amount of training data used. The area under the ROC curve (AUC) is used as the metric, with a lower AUC indicating better performance (an ideal AUC is 0.5). The L-GATr flow model consistently outperforms other models.
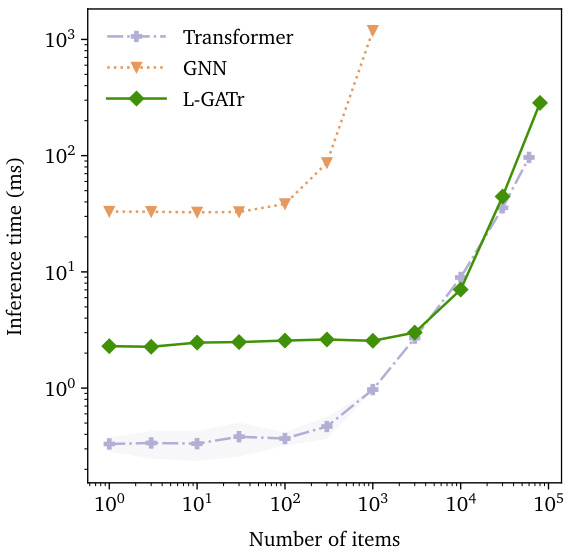
This figure compares the inference time (in milliseconds) of three different network architectures: L-GATr, Transformer, and a Graph Neural Network (GNN) as a function of the number of particles. The GNN runs out of memory above 1000 particles, whereas the other two scale well.
Full paper#