↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Modern information retrieval heavily relies on neural embedding models, with recent advancements focusing on multi-vector models for enhanced performance. However, these multi-vector models introduce significant computational challenges due to the complexity of similarity scoring. This research paper tackles this issue by proposing a new approach.
The proposed method, MUVERA, cleverly transforms multi-vector retrieval problems into single-vector problems. It achieves this by generating fixed dimensional encodings (FDEs) for both queries and documents. These FDEs maintain the essential information while enabling the use of efficient single-vector search algorithms (like maximum inner product search or MIPS). Experiments show that MUVERA outperforms existing approaches by achieving better accuracy with significantly reduced latency and memory footprint. The paper also provides theoretical justification for MUVERA’s accuracy and efficiency.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in information retrieval as it presents MUVERA, a novel and efficient algorithm that significantly improves the speed and accuracy of multi-vector retrieval. It addresses the computational bottleneck of existing methods, offering a substantial advancement in the field. The theoretical guarantees and empirical results open up new avenues for research, particularly in optimizing multi-vector representations and developing faster similarity search techniques.
Visual Insights#
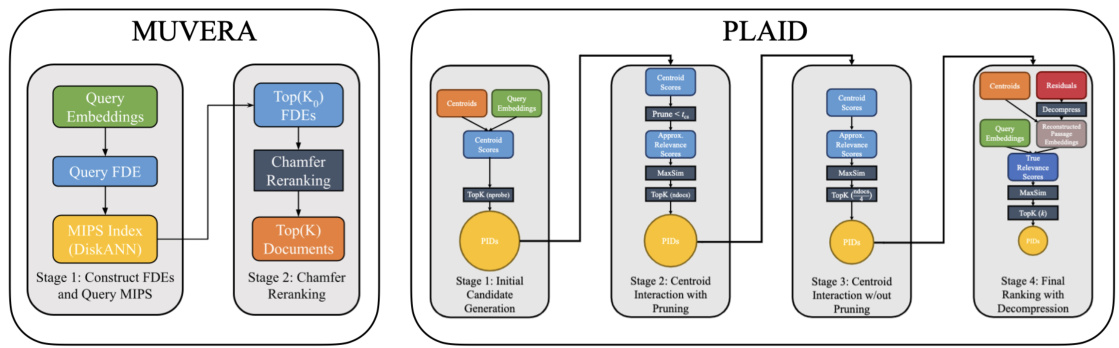
This figure compares the retrieval processes of MUVERA and PLAID. MUVERA uses a two-step process: First, it constructs fixed-dimensional encodings (FDEs) of queries and documents and performs a single-vector maximum inner product search (MIPS) using these FDEs. Then, it reranks the top K candidates using Chamfer similarity. In contrast, PLAID uses a more complex four-stage process that involves multiple rounds of candidate generation, centroid interaction (with and without pruning), and final re-ranking with decompression. The diagram highlights the relative simplicity and efficiency of MUVERA compared to PLAID.

This table presents a summary of the six BEIR datasets used in the paper’s experiments. It lists the number of queries and the size of the corpus (#Corpus) for each dataset. Importantly, it also shows the average number of embeddings per document (Avg # Embeddings per Doc), which is crucial for understanding the scale of the multi-vector retrieval problem and the relative computational costs of different approaches. This information is important because the number of embeddings directly impacts the complexity of the search process.
In-depth insights#
MV to SV Reduction#
The core idea of “MV to SV Reduction” in a multi-vector retrieval context centers on transforming complex, multi-vector representations into simpler, single-vector equivalents. This transformation is crucial because single-vector representations significantly improve computational efficiency in similarity search using optimized algorithms like Maximum Inner Product Search (MIPS). The challenge lies in ensuring that the single-vector representation faithfully captures the core semantic information embedded within the original multi-vector data, minimizing information loss during the transformation process. This involves careful consideration of the embedding’s structure and properties to create a suitable transformation scheme and the inherent trade-off between computational savings and accuracy. Effective “MV to SV Reduction” techniques are vital for scaling multi-vector retrieval systems to handle large datasets while maintaining or exceeding the retrieval performance of standard multi-vector approaches. The success of such methods often depends on strong theoretical guarantees and demonstrably robust empirical validation across diverse datasets and retrieval tasks. A key aspect is the development of algorithms that can efficiently and accurately map the high-dimensional multi-vector space into a lower-dimensional single-vector space, preserving semantic similarity.
FDE Approximation#
The concept of “FDE Approximation” in the context of a multi-vector retrieval system centers on efficiently approximating the complex Chamfer similarity between sets of vectors using a single, fixed-dimensional vector encoding. This approximation is crucial for scalability, as it allows leveraging optimized single-vector search methods instead of computationally expensive multi-vector techniques. The core idea is to create Fixed Dimensional Encodings (FDEs) for both queries and documents that preserve, as closely as possible, the relative similarity relationships defined by Chamfer. The effectiveness of this approximation hinges on the design of the encoding functions. Theoretical guarantees are essential to ensure the quality of the approximation, bounding the error introduced by simplifying multi-vector comparisons to single-vector operations. A well-designed FDE approximation algorithm enables a significant speedup in retrieval, often several orders of magnitude faster while maintaining high accuracy. Proofs and theoretical analysis of the approximation error are vital, establishing the reliability and precision of this approach for large-scale information retrieval tasks.
MUVERA Efficiency#
MUVERA’s efficiency stems from its novel approach to multi-vector retrieval (MVR). Instead of directly comparing multiple embeddings, as in traditional methods like PLAID, MUVERA cleverly transforms query and document sets into single, fixed-dimensional vectors (FDEs). This ingenious step allows the use of highly-optimized single-vector maximum inner product search (MIPS) algorithms, significantly accelerating the process. The effectiveness is further enhanced by theoretical guarantees proving that the FDE inner product well-approximates the multi-vector Chamfer similarity. In experiments, MUVERA consistently outperforms state-of-the-art methods, achieving comparable recall with substantially lower latency across various datasets. This efficiency boost is attributed to the reduced computational cost of using single-vector MIPS and the elimination of computationally expensive multi-stage pruning steps. Finally, MUVERA’s use of product quantization results in significantly smaller memory footprints without sacrificing significant retrieval accuracy, further boosting its overall efficiency.
Recall Enhancements#
Recall enhancement in information retrieval focuses on improving the accuracy of search results. This involves techniques to retrieve more relevant documents while minimizing irrelevant ones. Effective recall enhancement strategies leverage various approaches: from optimizing indexing and search algorithms (e.g., using advanced data structures or query expansion) to refining similarity measures (e.g., incorporating contextual information or semantic understanding). Key challenges include: balancing recall with precision (avoiding an excessive number of retrieved documents), dealing with noisy or ambiguous queries, and handling the scalability of the system for large datasets. Successful recall enhancements often involve a combination of methods: integrating multiple techniques to achieve superior performance than any single method would achieve in isolation. The evaluation of recall enhancement is critical, requiring the use of appropriate metrics and benchmark datasets to assess the effectiveness of proposed improvements. This is typically done by comparing recall@k (or other relevant metrics) against state-of-the-art approaches to quantify the performance gains and justify the value of a new recall enhancement technique.
Future of FDEs#
The future of Fixed Dimensional Encodings (FDEs) in multi-vector retrieval is promising, building on their demonstrated ability to achieve high recall with significantly lower latency than existing methods. Further research should focus on improving the approximation guarantees of FDEs, potentially through exploring alternative hashing techniques or dimensionality reduction methods beyond random projections. Investigating the impact of different data distributions on FDE performance, and developing efficient methods for handling extremely high-dimensional data, are crucial next steps. Exploring adaptive methods that adjust the FDE dimensionality based on the query characteristics could significantly improve efficiency. Combining FDEs with other advanced techniques, such as quantization and indexing strategies, holds the potential to create even more efficient and scalable multi-vector retrieval systems. The inherent simplicity and data-oblivious nature of FDEs make them readily adaptable to a variety of applications and datasets; making them particularly attractive for deployment in resource-constrained environments. Finally, theoretical analysis of the FDE approximation error in relation to specific data characteristics will further refine the method and solidify its position as a foundational approach for future multi-vector retrieval advances.
More visual insights#
More on figures

This figure illustrates the process of generating Fixed Dimensional Encodings (FDEs) in MUVERA. It uses SimHash to partition the data space into clusters. The process shows how query and document multi-vector sets are transformed into single fixed-dimensional vectors (FDEs) by summarizing embeddings within each cluster. The figure simplifies the process to 2 dimensions and 3 SimHashes for clarity, while the actual implementation handles higher dimensions and multiple repetitions for improved accuracy. The final FDEs are obtained by concatenating the cluster summaries, but inner projections and a cluster filling step (not shown) are also performed to improve quality.
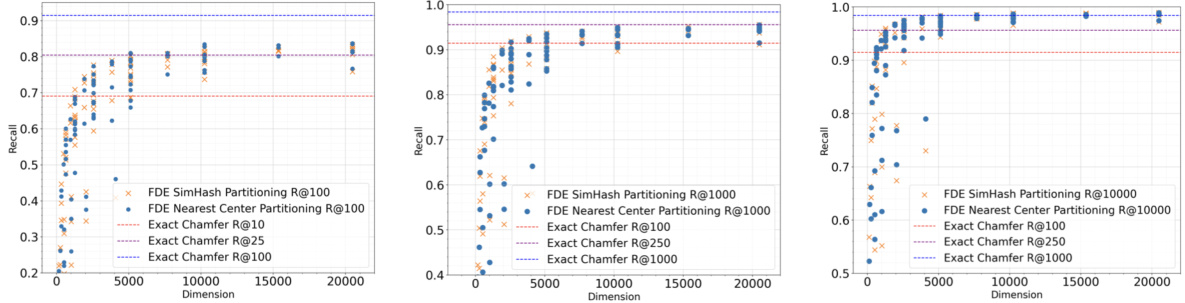
This figure shows the relationship between the dimensionality of the Fixed Dimensional Encoding (FDE) and its recall performance on the MS MARCO dataset. Three different recall levels (@100, @1000, @10000) are plotted for different FDE parameters. The dotted lines represent the recall achieved using the exact Chamfer similarity calculation, providing a baseline for comparison. The figure demonstrates how increasing the dimensionality of the FDEs improves recall, gradually approaching the performance of the exact Chamfer similarity.

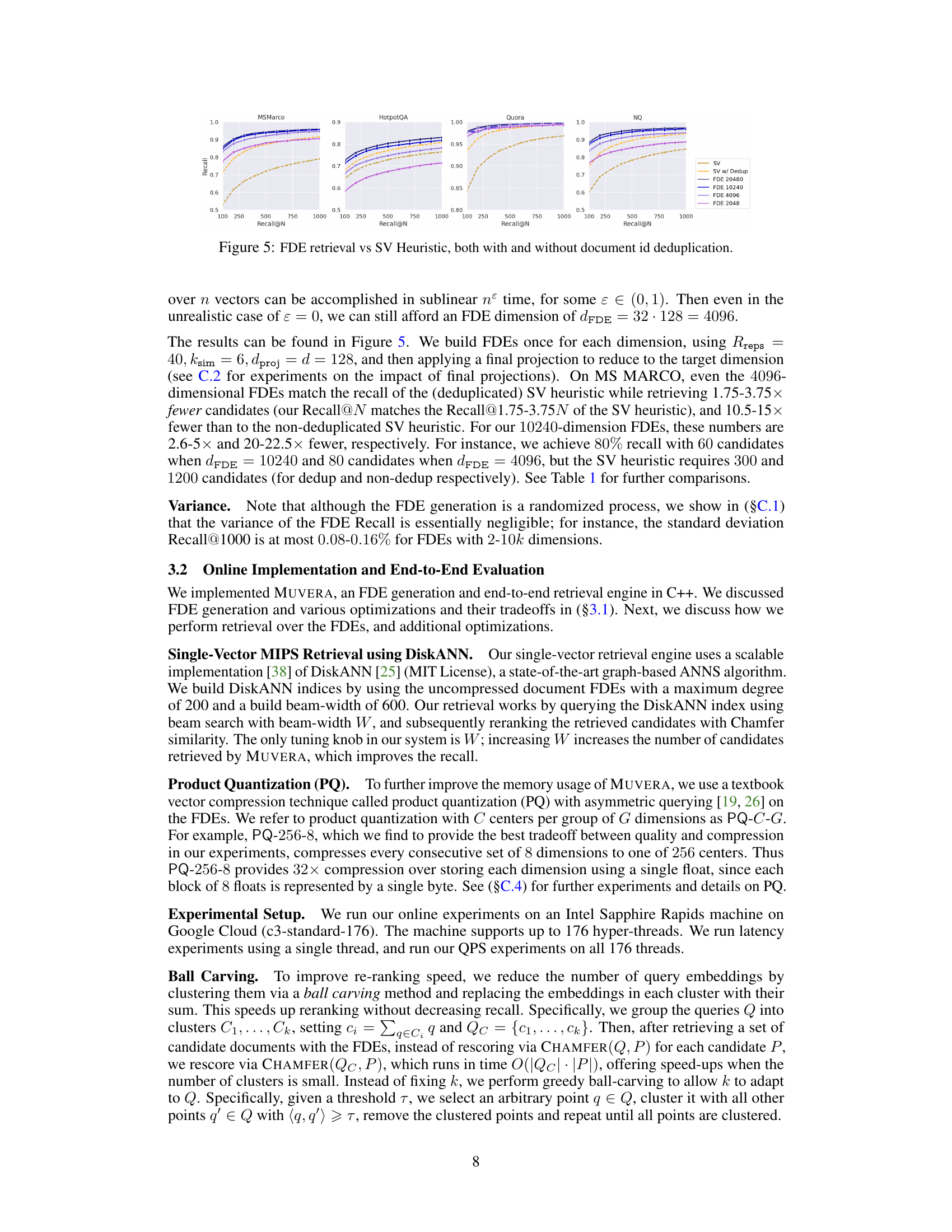
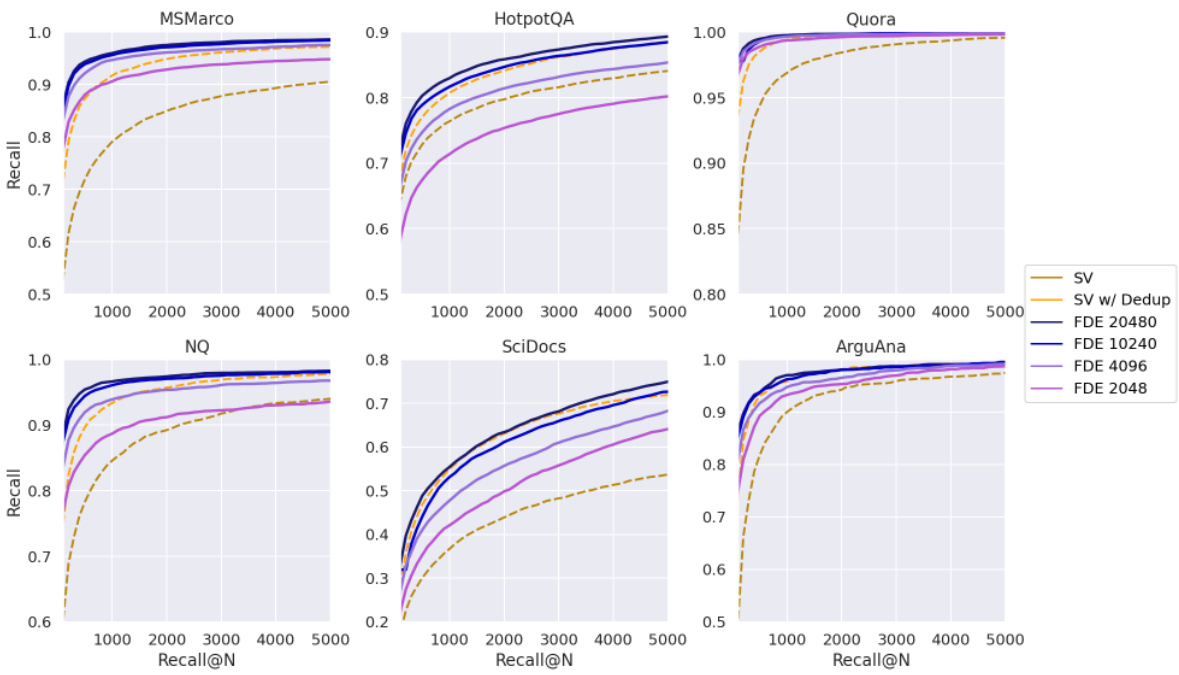
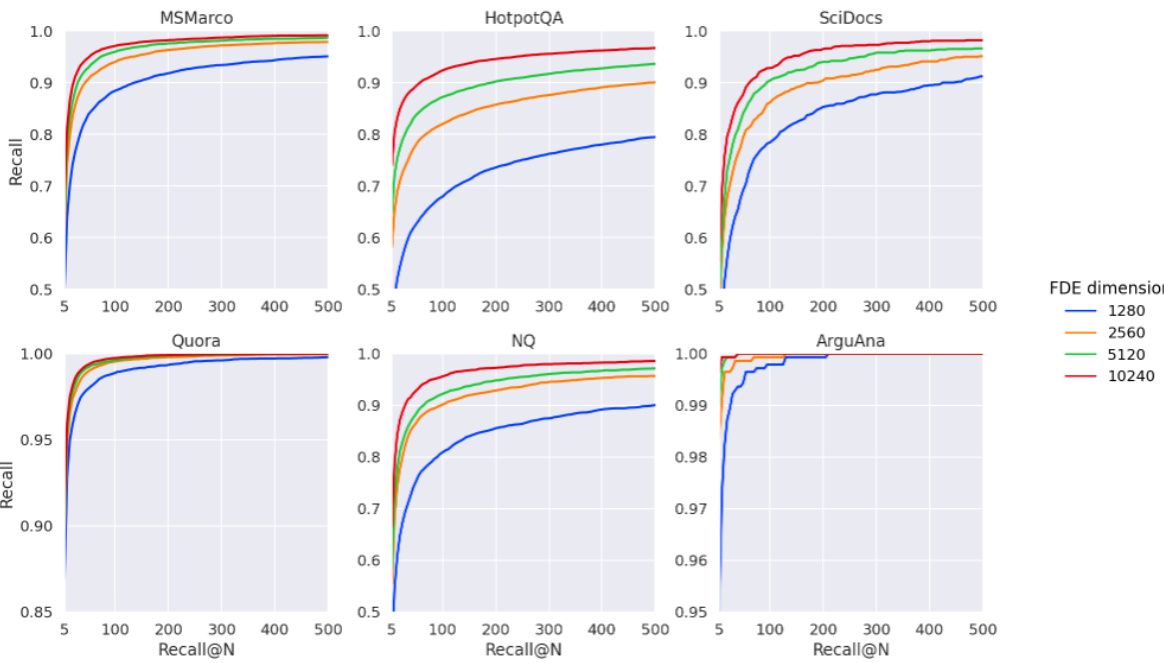
This figure compares the recall performance of the proposed FDE (Fixed Dimensional Encoding) method against the Single-Vector heuristic method at different recall levels (Recall@100-5000) across six different datasets. The FDE method uses four different dimensionality settings for its embeddings, while the SV heuristic uses two approaches: one without deduplication and one with deduplication of document IDs. The graph shows the recall at different N values for each method, allowing for a clear comparison of the performance on different datasets and with different dimensionalities.

This figure compares the performance of Fixed Dimensional Encoding (FDE) based retrieval against the Single-Vector (SV) heuristic, a method commonly used in multi-vector retrieval systems like PLAID. The SV heuristic involves querying a single-vector MIPS index for each query token to find initial candidate documents and then re-ranking them using the Chamfer similarity. The figure shows the Recall@N (the fraction of queries where the Chamfer 1-nearest neighbor is among the top-N most similar in either method) for both approaches, with and without deduplication (removing duplicate documents from the candidate list) of the SV heuristic results. The results demonstrate that FDEs significantly outperform the SV heuristic, especially in achieving high recall with fewer candidate documents.
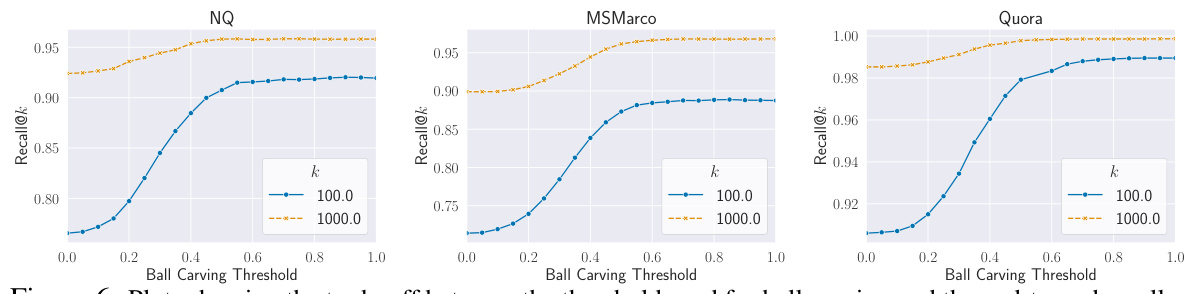
This figure displays the relationship between the threshold used for ball carving and the resulting end-to-end recall at k=100 and k=1000 for three different datasets: MS MARCO, Quora, and NQ. The x-axis represents the ball carving threshold, and the y-axis represents the Recall@k. Each line shows the Recall@k as the threshold changes. The plots demonstrate that there is a trade-off between the recall and the threshold value. At lower thresholds, more query embeddings are used leading to higher recall, and at higher thresholds, fewer embeddings result in lower recall, however, with significant computational speed-up.
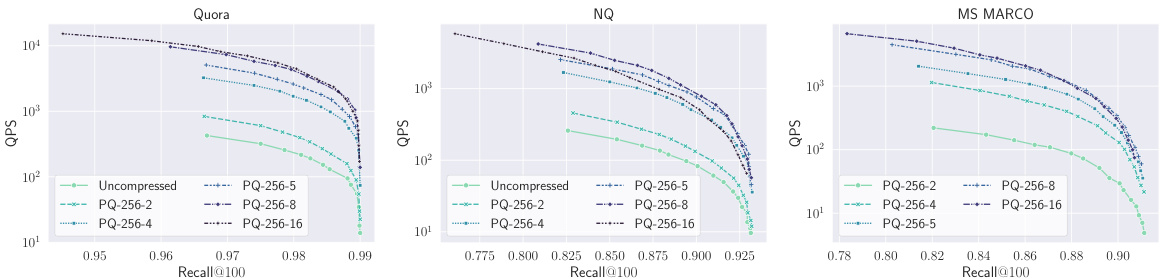
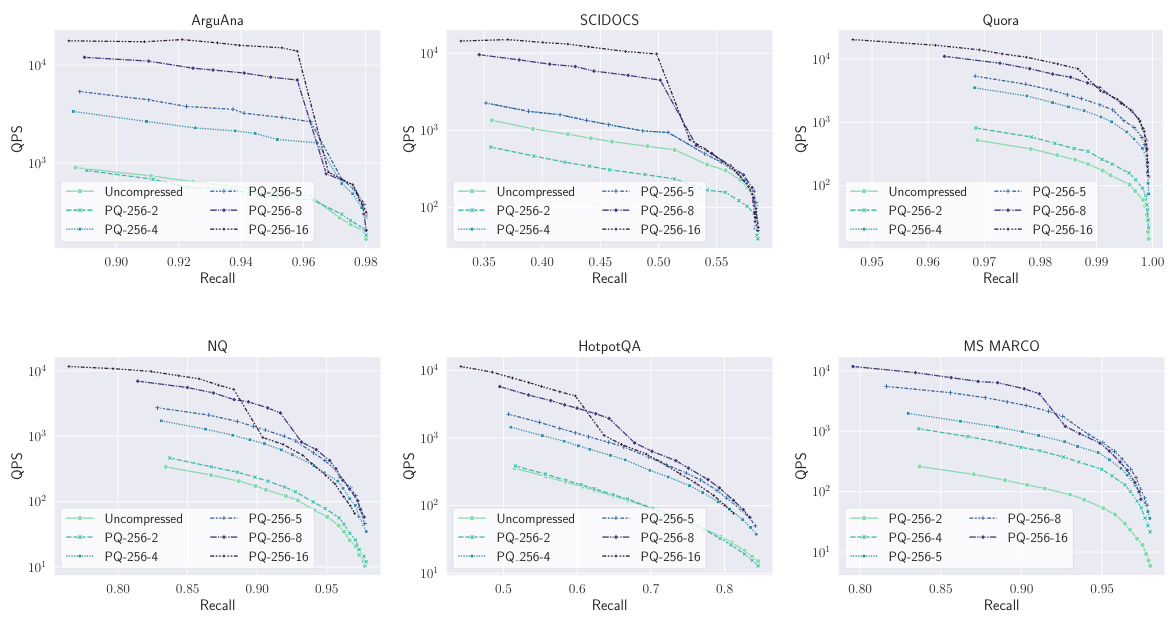
This figure shows the trade-off between the speed (queries per second, QPS) and the recall@100 of the MUVERA model for six different datasets from the BEIR benchmark. Different curves represent the results obtained using various product quantization (PQ) methods to compress the 10240-dimensional fixed dimensional encodings (FDEs). The plot helps to visualize how compression impacts both retrieval speed and accuracy.

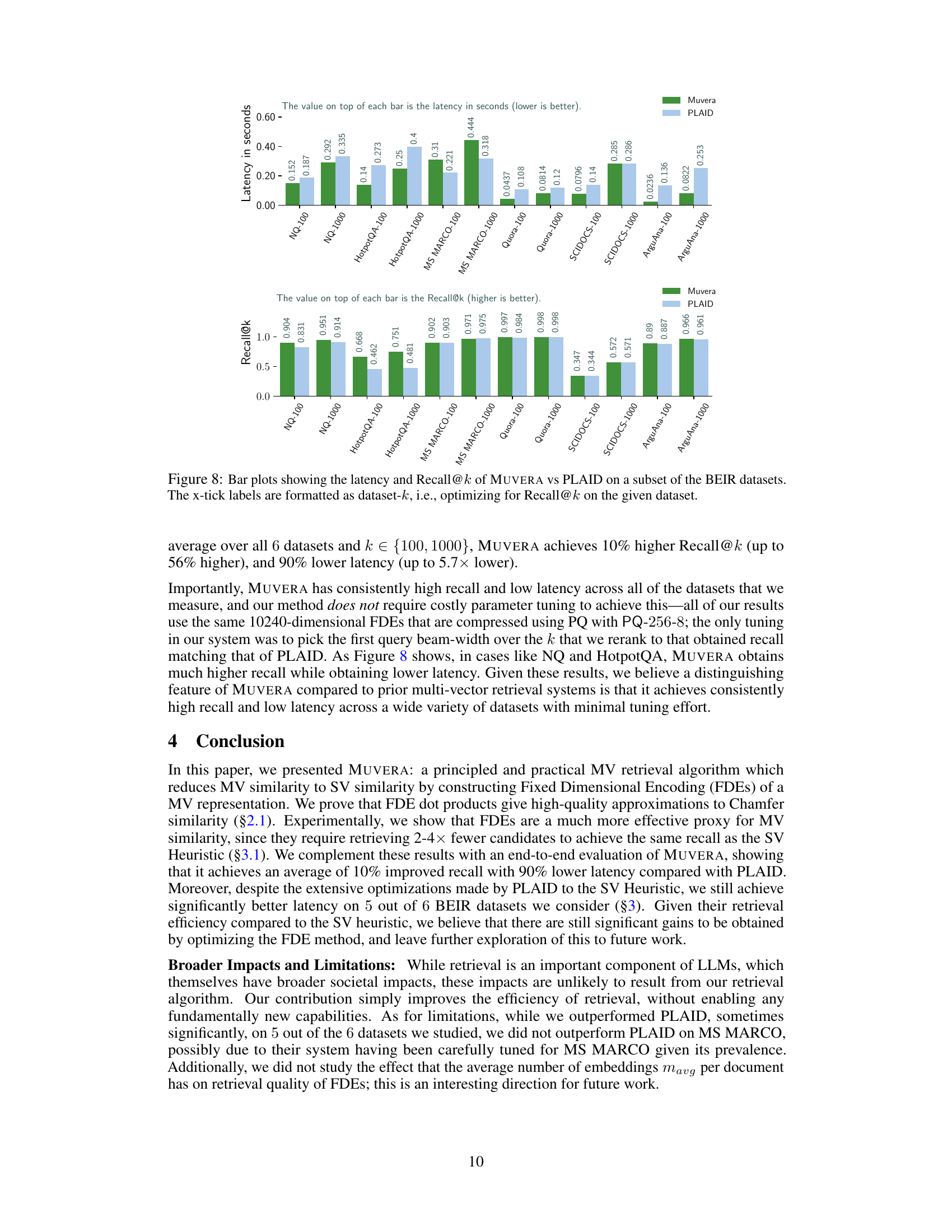
This figure compares the performance of MUVERA and PLAID on several BEIR datasets for different recall@k values (k=100 and k=1000). Two separate bar charts are shown, one for latency (lower is better) and one for recall (higher is better). Each bar represents a specific dataset and k value combination. The chart shows MUVERA consistently outperforms PLAID in terms of latency while maintaining comparable recall, often exceeding PLAID’s recall.
This figure shows the relationship between the recall of the Fixed Dimensional Encoding (FDE) method and its dimensionality on the MS MARCO dataset. It presents three plots representing Recall@100, Recall@1000, and Recall@10000 across different FDE dimensionalities. Each plot includes multiple lines, representing different parameter settings used for generating FDEs, revealing how different parameters impact recall. The dotted lines in each plot represent the recall achieved using the exact Chamfer similarity, providing a benchmark for comparing the accuracy of FDE approximations against the optimal score.

This figure compares the recall performance of the proposed FDE (Fixed Dimensional Encoding) retrieval method against the single-vector (SV) heuristic retrieval method. The SV heuristic is a common approach in multi-vector retrieval that uses single-vector MIPS (Maximum Inner Product Search) to find initial candidates, which are then re-ranked using Chamfer similarity. The figure shows that FDE retrieval consistently outperforms the SV heuristic, especially when document ID deduplication is considered. The FDE method achieves higher Recall@N (number of relevant documents retrieved among the top N) than the SV heuristic, even when the SV heuristic uses a larger number of candidates (as indicated by the larger Recall@N values on the x-axis for the SV heuristic). The results suggest that the FDE method is a more effective approach for multi-vector retrieval.
This figure displays the relationship between the dimensionality of Fixed Dimensional Encodings (FDEs) and their recall performance on the MS MARCO dataset. It shows how recall@100, recall@1000, and recall@10000 change as the dimensionality of FDEs increases, and compares those results to the recalls achieved using exact Chamfer similarity scoring. The dotted lines represent exact Chamfer results, while the solid lines represent results from different sets of FDE parameters.

This figure shows the trade-off between the threshold used for ball carving and the end-to-end queries per second (QPS) on the MS MARCO dataset. Two lines are plotted, one showing sequential re-ranking performance and another parallel. As the threshold increases (meaning fewer clusters are made), the QPS for sequential re-ranking increases, while the QPS for parallel re-ranking stays relatively flat and slightly lower than the sequential approach.

This figure shows the trade-off between the speed (queries per second, QPS) and the recall@100 of the MUVERA model on six different datasets from the BEIR benchmark. Different curves represent different product quantization (PQ) methods used to compress the 10240-dimensional fixed dimensional encodings (FDEs). The plot demonstrates the impact of compression on both speed and retrieval accuracy. Generally, higher compression leads to higher QPS but slightly lower recall.
This figure compares the retrieval processes of MUVERA and PLAID. MUVERA uses a two-stage process: First, it constructs fixed dimensional encodings (FDEs) and performs a query maximum inner product search (MIPS). Second, it performs Chamfer reranking. In contrast, PLAID uses a four-stage process involving initial candidate generation, centroid interaction with pruning, centroid interaction without pruning, and final ranking with decompression. The diagram illustrates the multiple steps in PLAID’s process, highlighting its complexity compared to MUVERA’s streamlined approach.
More on tables

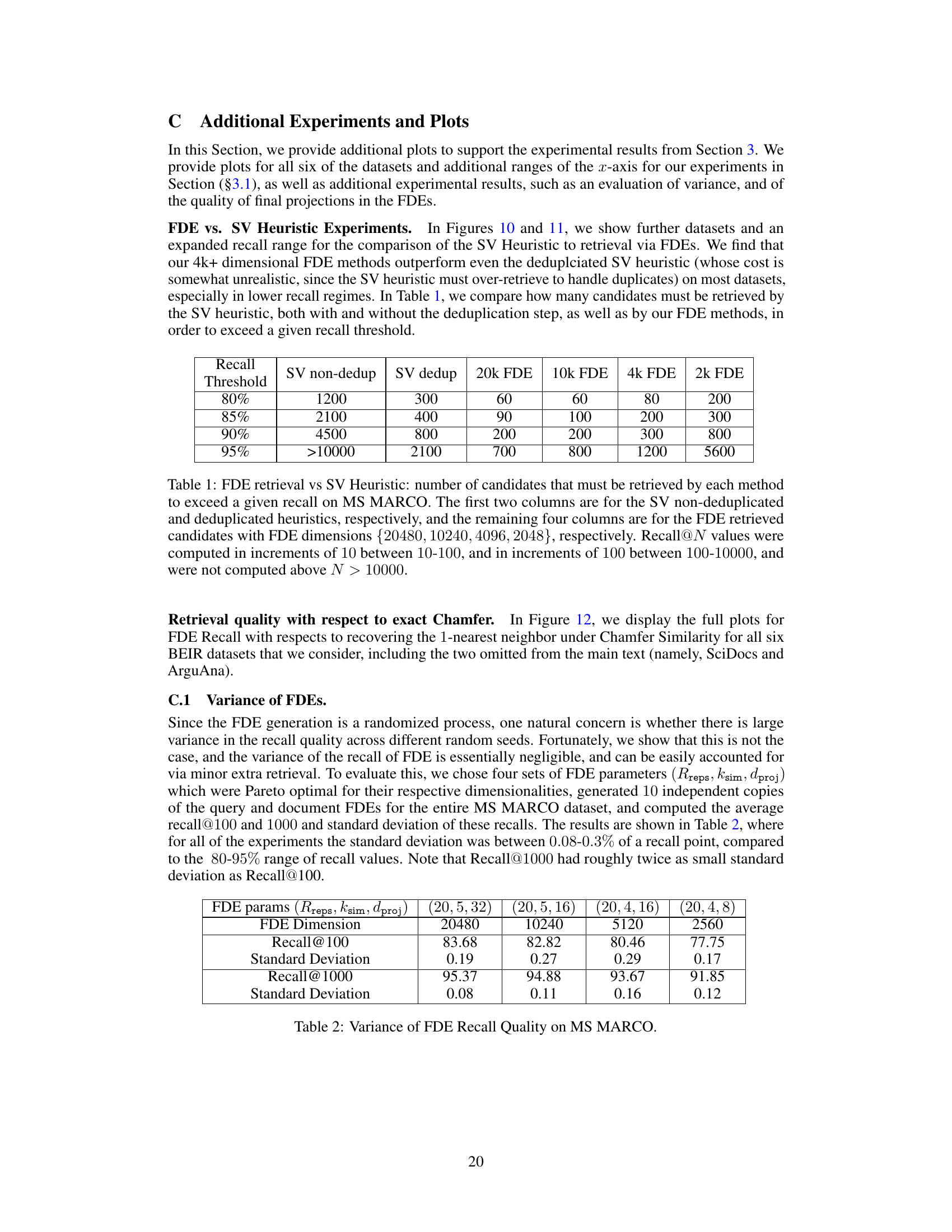
This table compares the number of candidates that need to be retrieved by different methods (Single-vector heuristic with and without deduplication, and FDE with different dimensions) to achieve certain recall thresholds (80%, 85%, 90%, 95%) on the MS MARCO dataset. It shows that FDE consistently requires far fewer candidates than the single-vector heuristic to reach the same recall levels.

This table shows the variance of FDE recall quality on the MS MARCO dataset for different FDE parameter settings. It demonstrates that even with a randomized process for generating FDEs, the recall remains stable, with standard deviations generally less than 0.3% of the recall value.

This table compares the recall quality of Fixed Dimensional Encodings (FDEs) with and without a final projection step. The experiment is performed on the MS MARCO dataset with varying FDE dimensions (2460 and 5120) to assess the impact of the final projection on retrieval performance. The results are presented as recall@100, recall@1000, and recall@10000.

This table presents the recall quality of Fixed Dimensional Encodings (FDEs) with and without final projections. The results show the recall@100, recall@1000, and recall@10000 for FDEs with dimensions 10240 and 20480, both with and without a final projection step. The data demonstrates the impact of the final projection on recall performance at different retrieval thresholds.
Full paper#