↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep Equilibrium Models (DEQs) offer promising advantages in deep learning, but ensuring their robustness against adversarial attacks is crucial for safe deployment, especially in security-sensitive applications. Existing certification methods for DEQs using deterministic techniques are computationally expensive and limited to specific DEQ architectures. This creates a major hurdle for using DEQs in real-world scenarios with large datasets.
This research introduces Serialized Random Smoothing (SRS), a novel randomized smoothing approach to address these limitations. SRS leverages historical information to significantly reduce redundant computation. The researchers also derive a new certified radius estimation, ensuring theoretical correctness. Experimental results on image recognition datasets show that SRS accelerates DEQ certification by up to 7x with minimal accuracy loss, enabling certification on large-scale datasets like ImageNet for the first time.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI security and deep learning. It presents a novel approach for efficiently certifying the robustness of Deep Equilibrium Models (DEQs), a critical issue in deploying these models in safety-critical applications. The proposed Serialized Random Smoothing (SRS) significantly accelerates the certification process, making it feasible for large-scale datasets. This opens avenues for broader adoption of DEQs and improves the trustworthiness of AI systems.
Visual Insights#

The figure compares the standard randomized smoothing method for Deep Equilibrium Models (DEQs) and the proposed Serialized Randomized Smoothing (SRS) method. Standard randomized smoothing independently processes each noisy sample, requiring computation for all D layers in the DEQ. In contrast, SRS leverages the previous sample’s computed representation as the initialization for the next sample. This significantly reduces computation time by processing only S layers (S « D) and then utilizes correlation-eliminated certification to estimate a certified robustness radius.

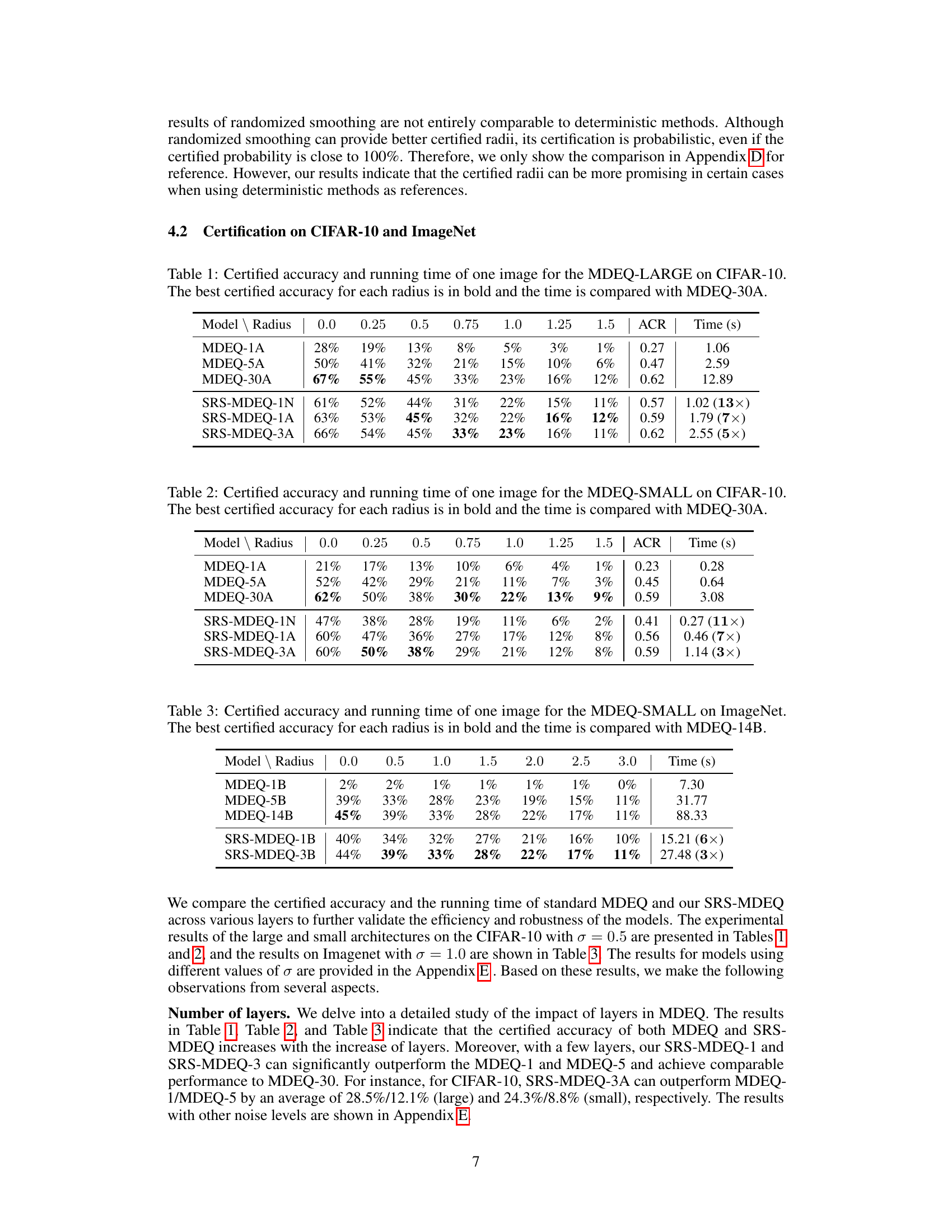
This table presents the certified accuracy and running time for a single image using the MDEQ-LARGE model on the CIFAR-10 dataset. It compares the standard MDEQ model with varying numbers of layers (1, 5, and 30) against the proposed Serialized Random Smoothing (SRS) method also with varying numbers of layers (1 and 3) using different solvers (Naive and Anderson). The best certified accuracy for each radius is highlighted in bold, and the running time for each model is shown relative to the MDEQ-30A model to illustrate the speedup achieved by SRS.
In-depth insights#
DEQ Robustness#
The robustness of Deep Equilibrium Models (DEQs) against adversarial attacks is a crucial area of research. Existing deterministic approaches like interval bound propagation and Lipschitz bounds struggle to certify robustness on large-scale datasets and are limited to specific DEQ architectures. This paper introduces a novel randomized smoothing technique, Serialized Randomized Smoothing (SRS), to address these limitations. SRS leverages historical information to significantly reduce computational costs, achieving up to a 7x speedup in certification without sacrificing accuracy. The core innovation is a new certified radius estimation for SRS that theoretically guarantees correctness despite the introduction of computation-saving correlations. This work is significant as it establishes a practical approach for certifying the robustness of DEQs on large-scale datasets, such as ImageNet, which was previously intractable due to high computational demands. Future research could explore further optimizations of the SRS algorithm, and investigations into its applicability to other implicit model architectures would also be valuable. The effectiveness of SRS across various solvers (Anderson, Broyden, Naive) and the theoretical underpinnings of the improved certification method represent key contributions.
SRS Approach#
The Serialized Randomized Smoothing (SRS) approach, as presented in the research paper, offers a significant advancement in certifying the robustness of Deep Equilibrium Models (DEQs). Its core innovation lies in addressing the computational redundancy inherent in standard randomized smoothing techniques applied to DEQs. By leveraging previously computed information from the fixed-point solvers, SRS substantially accelerates the certification process. This is achieved by using the previous noisy sample’s fixed-point representation as the initialization for the next sample’s computation, thereby significantly reducing the number of iterations required for convergence. However, this optimization introduces a correlation between successive predictions, which necessitates a novel correlation-eliminated certification technique. This technique ensures the theoretical robustness guarantees remain intact despite the optimization, providing a robust and efficient method for certifying DEQs’ robustness at scale. The results demonstrate a substantial speedup, accelerating the certification process by up to 7 times while maintaining comparable certified accuracy.
Certified Radius#
The concept of “Certified Radius” in the context of a research paper on the robustness of Deep Equilibrium Models (DEQs) refers to a quantifiable measure of a model’s resilience against adversarial attacks. It signifies the size of a hypersphere around a data point within which any perturbation will not alter the model’s prediction. This certification is crucial for ensuring the model’s reliability and trustworthiness, especially in security-sensitive applications. The paper likely explores different methods for computing the certified radius, comparing their computational efficiency and accuracy. A larger certified radius is preferable but often comes at the cost of increased computational time, therefore, finding a balance between robustness and computational efficiency is likely a key challenge explored within the research. The theoretical underpinnings of the chosen method(s) to compute the certified radius, possibly including formal guarantees or bounds, would be a central focus. The study’s findings likely demonstrate how their approach achieves improved performance compared to existing techniques, particularly concerning the size of the certified radius achievable while maintaining or even improving the computational efficiency.
Efficiency Gains#
The efficiency gains in this research stem from a novel approach called Serialized Random Smoothing (SRS). SRS cleverly addresses the computational redundancy inherent in traditional randomized smoothing techniques for Deep Equilibrium Models (DEQs). By leveraging historical information from previous iterations, SRS significantly accelerates the convergence of fixed-point solvers within DEQs. This results in a substantial reduction in computation time, often by a factor of 7x, without significant loss of certified accuracy. The efficiency gains are particularly noteworthy for large-scale datasets, where the computational cost of traditional methods becomes prohibitive. The paper provides both theoretical and empirical evidence supporting the speedup achieved through SRS, demonstrating the effectiveness of this novel approach. The key to this speedup lies in the efficient reuse of previously computed information, thereby mitigating redundant calculations and improving the overall efficiency of the certification process. This makes the certification of DEQs more practical for real-world applications.
Future Works#
Future research directions stemming from this work could explore extending Serialized Randomized Smoothing (SRS) to other implicit model architectures, beyond Deep Equilibrium Models (DEQs). Investigating the applicability of SRS to different types of fixed-point solvers and exploring ways to further optimize the computational efficiency of SRS are also important. A key area is to develop more robust theoretical guarantees for the certified radius in SRS, potentially through advanced statistical techniques. Furthermore, research could focus on empirically evaluating the robustness of SRS-DEQs against a wider range of adversarial attacks, beyond those considered in the paper, to establish greater confidence in its effectiveness against real-world threats. Finally, a valuable investigation would involve analyzing the trade-off between computational cost and certified accuracy across different model sizes and datasets to better understand the practical limits and benefits of this novel technique.
More visual insights#
More on figures
The figure compares the standard randomized smoothing approach for DEQs with the proposed Serialized Randomized Smoothing (SRS) approach. The standard method performs many independent forward passes through the full depth (D) of the DEQ for each noisy sample. In contrast, the SRS method leverages the previous DEQ output as initialization for subsequent noisy sample processing, thus drastically reducing computation by only requiring a few (S) layers. Both methods conclude with correlation-eliminated certification to determine a certified robustness radius.
This figure compares the standard randomized smoothing approach with the proposed Serialized Randomized Smoothing (SRS). The standard approach computes the fixed point for each noisy sample independently, requiring many iterations. In contrast, SRS leverages the previous fixed point as the starting point for the next computation, significantly reducing the number of layers required. The figure also highlights the correlation-eliminated certification used in SRS to estimate a certified radius despite the correlation between the noisy samples.

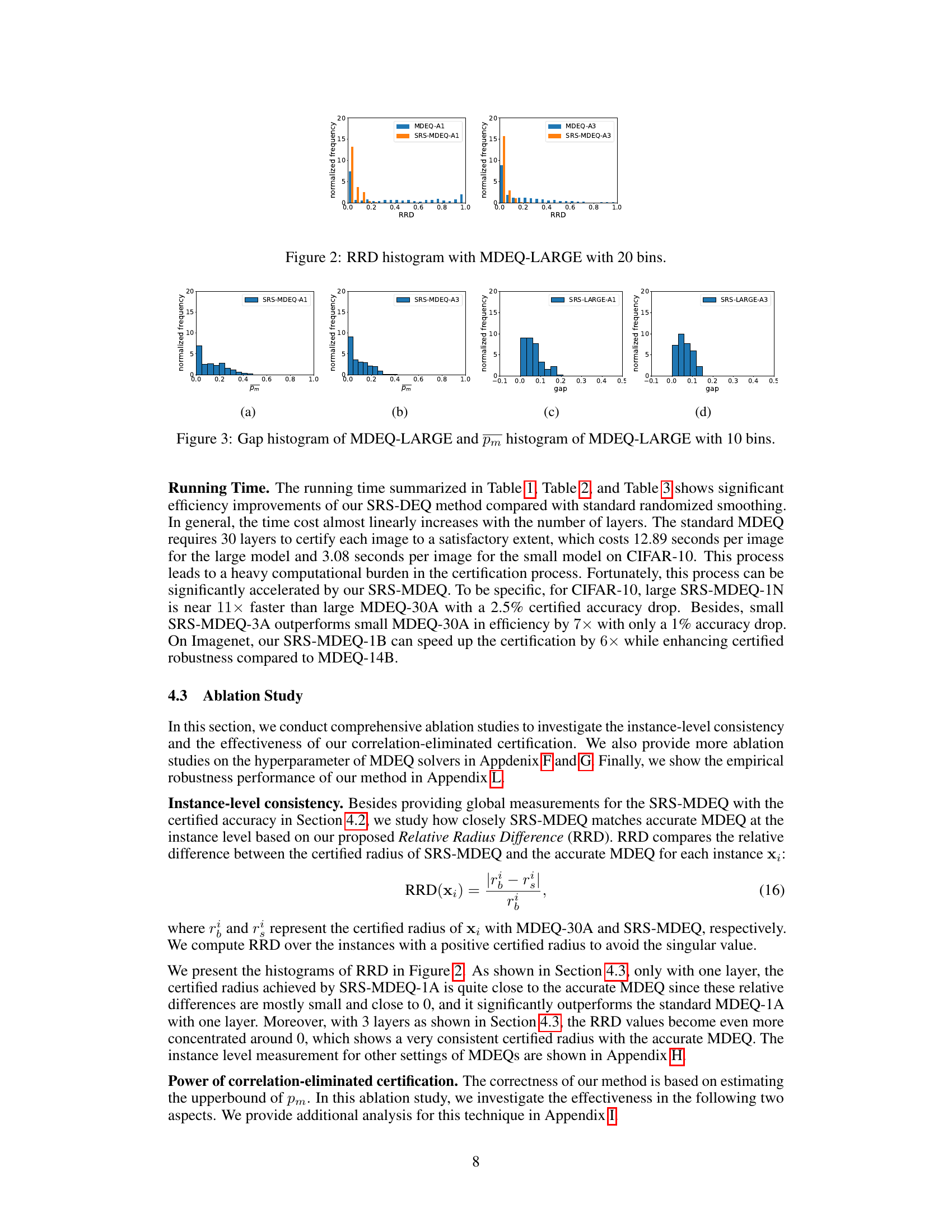
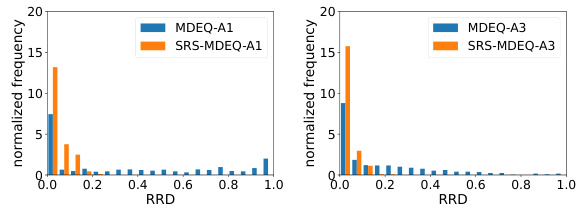
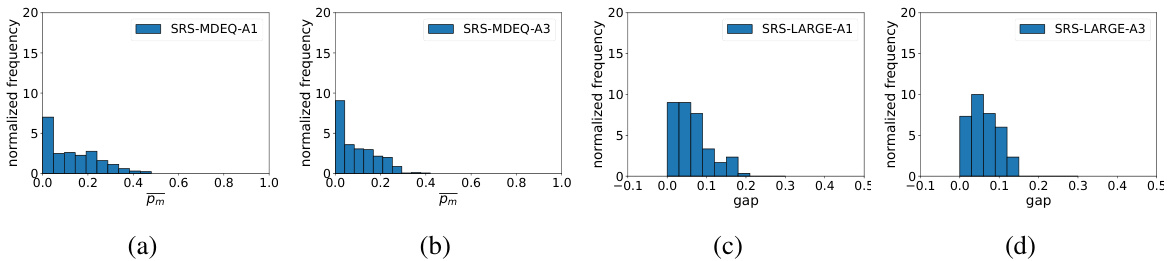
This figure shows the distribution of Relative Radius Difference (RRD) for the MDEQ-LARGE model. RRD measures how close the certified radius of the proposed Serialized Randomized Smoothing (SRS) method is to the actual certified radius obtained with the standard method. A smaller RRD indicates better consistency between the two methods. The histogram shows the frequency of different RRD values, allowing for analysis of the method’s performance at the instance level.

The figure illustrates the difference between standard randomized smoothing for DEQs and the proposed Serialized Randomized Smoothing (SRS). In standard DEQ, each sample goes through all D layers during forward propagation. SRS-DEQ leverages the output of the previous sample as initialization for the next sample, significantly reducing computation by using only S layers where S « D. The method also utilizes a correlation-eliminated certification to properly estimate the certified radius.

This figure compares the standard randomized smoothing approach with the proposed Serialized Randomized smoothing (SRS). The standard approach involves multiple independent runs of the DEQ model for each noisy input sample. In contrast, SRS leverages the output of the previous DEQ run as the initialization for the next, thereby reducing computational redundancy by reusing historical information. The figure also highlights that SRS employs a novel correlation-eliminated certification technique to estimate the certified radius, ensuring theoretical guarantees despite the reduced computational cost.

This figure compares the standard randomized smoothing approach for Deep Equilibrium Models (DEQs) with the proposed Serialized Randomized Smoothing (SRS). The standard approach processes each noisy sample independently through the full D layers of the DEQ. In contrast, SRS leverages the output from the previous sample to initialize the next sample’s computation, reducing the number of layers (S) needed to convergence and speeding up the process significantly. After obtaining predictions for all samples using both methods, a correlation-eliminated certification technique is employed in SRS to estimate the certified radius.

The figure compares the standard randomized smoothing approach for Deep Equilibrium models (DEQs) with the proposed Serialized Randomized Smoothing (SRS). The standard approach involves passing each sample through all D layers of the DEQ multiple times for different noise samples, leading to high computational cost. In contrast, SRS leverages the previous representation (from the previous noisy sample) as initialization for subsequent noisy samples, enabling faster convergence with only S layers (S « D). The certified radius is then estimated using correlation-eliminated certification.

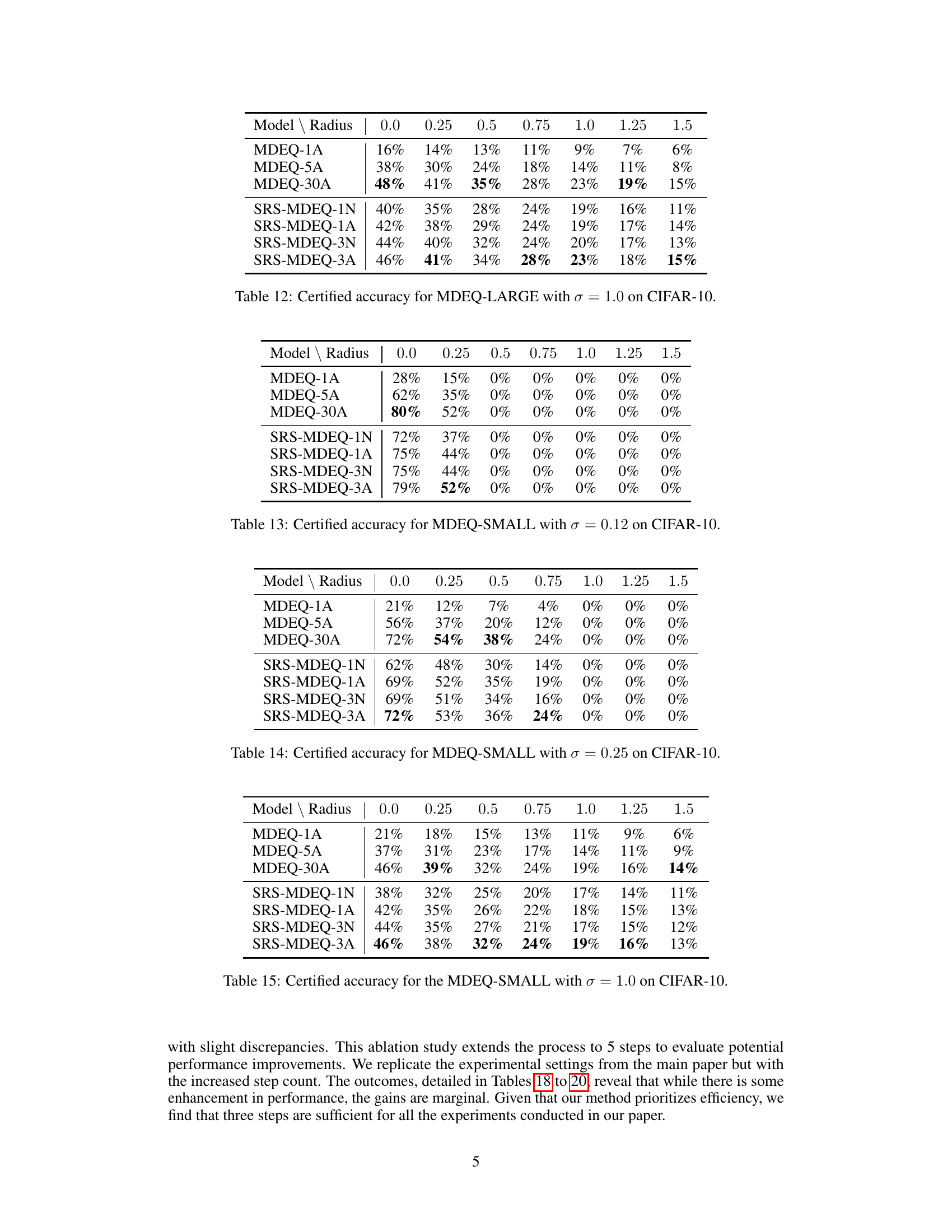
The figure shows the impact of the number of samplings (N) on the certified accuracy of the MDEQ-SMALL model using 3-step solvers (Anderson and Naive). It displays the certified accuracy curves for three different sampling numbers: N=1,000, N=10,000, and N=100,000, across a range of radii. The plots illustrate the robustness of the results to the choice of sampling number, with consistent performance observed across the three different N values.

This figure compares the standard randomized smoothing method for Deep Equilibrium Models (DEQs) and the proposed Serialized Random Smoothing (SRS) approach. The standard DEQ processes each sample through all D layers. In contrast, SRS-DEQ leverages the output from previous samples to initialize the process, reducing computation to S layers (S is much less than D). This speeds up computation, and a novel correlation-eliminated certification method is used to estimate the certified robustness radius.
This figure compares the standard randomized smoothing method for Deep Equilibrium models (DEQs) with the proposed Serialized Randomized Smoothing (SRS). The standard method independently processes each noisy sample through all D layers of the DEQ, whereas the SRS method leverages the previous sample’s representation as the initialization for the next, reducing computation time. Both methods use a final correlation-eliminated certification step to estimate the certified radius.
The figure compares standard randomized smoothing for DEQs with the proposed Serialized Randomized Smoothing (SRS). Standard DEQ processing involves propagating each sample through all D layers, requiring extensive computation. SRS improves efficiency by leveraging the previous layer’s representation as the initialization for the next layer. This reduces the number of layers processed (S) significantly, accelerating the certification process while maintaining accuracy. The correlation-eliminated certification method is used in SRS to address the correlations introduced by the re-use of prior layer information and provide theoretical guarantees on its robustness.
More on tables
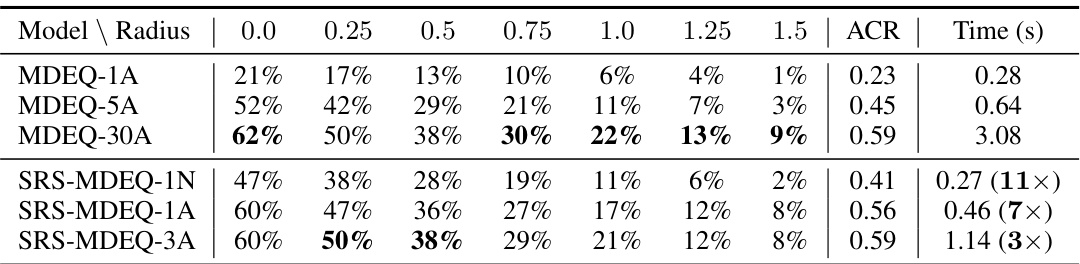
This table presents the certified accuracy and running time for different MDEQ models (MDEQ-1A, MDEQ-5A, MDEQ-30A) and the proposed SRS-MDEQ models (SRS-MDEQ-1N, SRS-MDEQ-1A, SRS-MDEQ-3A) on the CIFAR-10 dataset. The results are shown for various certified radii (0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5). The best certified accuracy for each radius is highlighted in bold. The running time for each model is presented, and its speedup compared to the MDEQ-30A model is shown in parentheses.
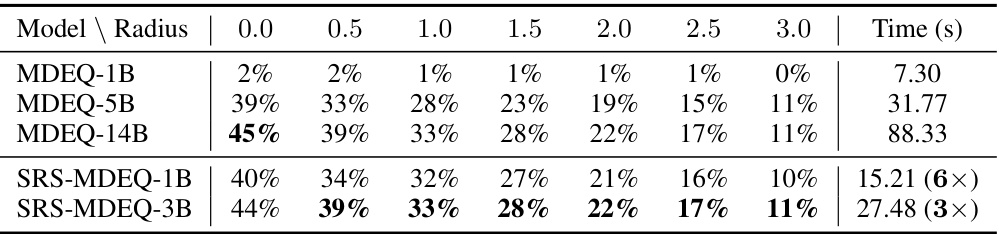
This table presents the certified accuracy and running time for the MDEQ-SMALL model on the ImageNet dataset. The results are shown for various certified radii (0.0 to 3.0). The best certified accuracy for each radius is highlighted in bold. The table also compares the running times of the standard MDEQ-14B model with the proposed SRS-MDEQ-1B and SRS-MDEQ-3B models, showing the speedup achieved by the SRS approach. The speedup factors are indicated in parentheses.

This table presents the certified accuracy and running time for classifying a single image using the MDEQ-LARGE model on the CIFAR-10 dataset. Different certified radii are tested, and the best accuracy achieved for each radius is highlighted in bold. The table also compares the runtime of the proposed Serialized Random Smoothing (SRS) approach to the standard MDEQ-30A approach, demonstrating the speedup achieved by SRS.

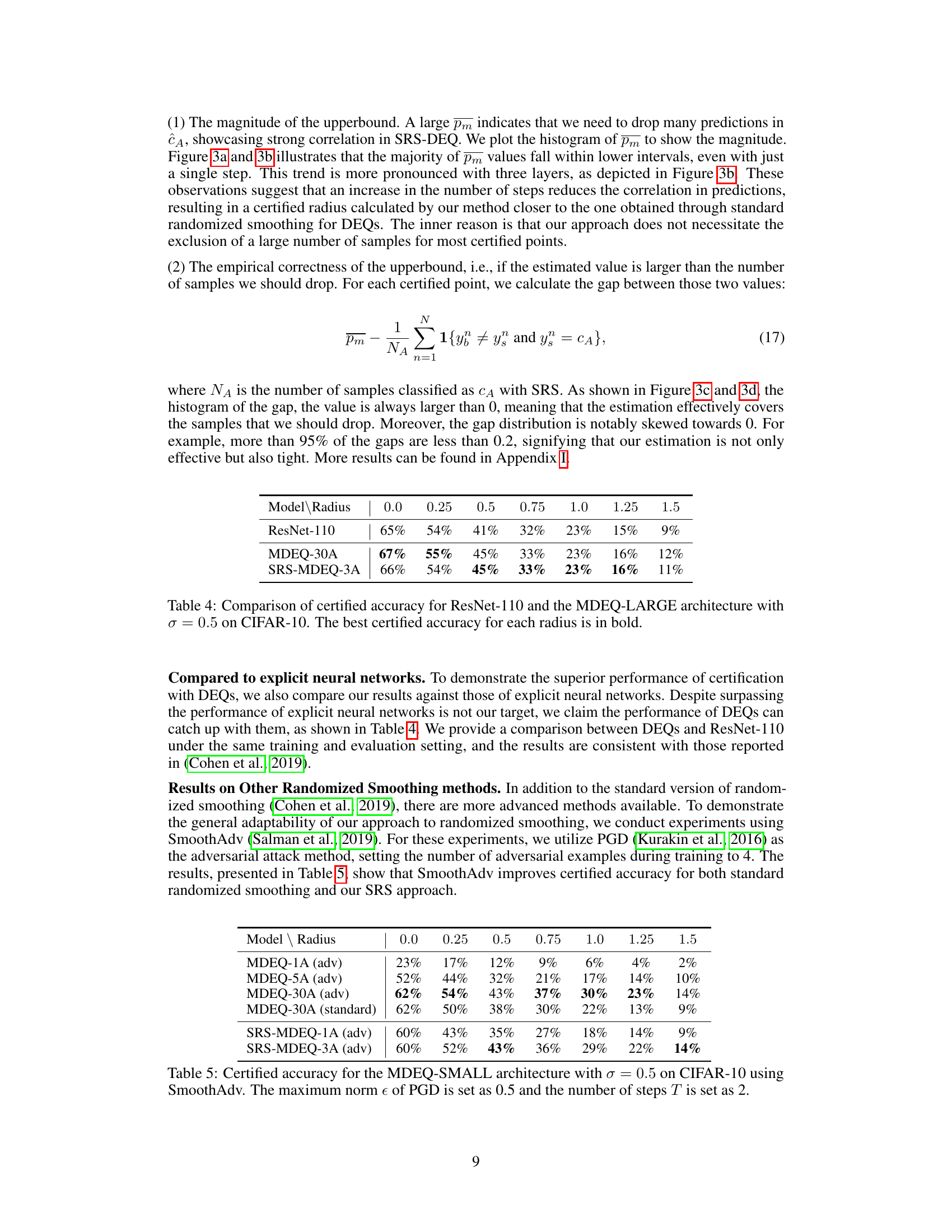
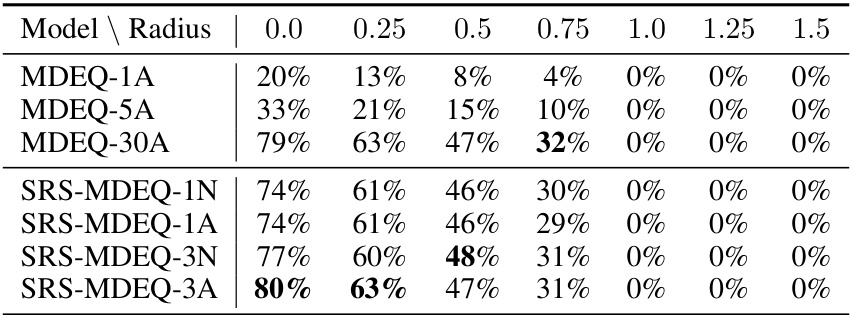
This table presents the certified accuracy results for the MDEQ-SMALL architecture on the CIFAR-10 dataset using SmoothAdv, a more advanced randomized smoothing method. The experiment uses Projected Gradient Descent (PGD) with a maximum norm of 0.5 and 2 steps. The results are compared with standard randomized smoothing results for various numbers of layers in the MDEQ model. It highlights the impact of SmoothAdv on the certified accuracy of DEQs for different levels of perturbation.
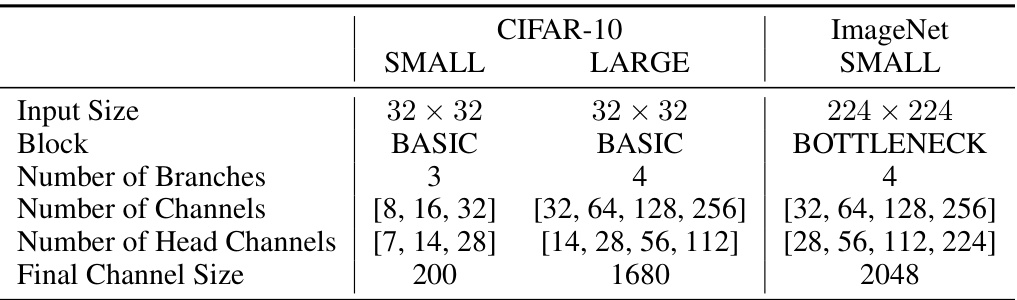
This table lists the hyperparameters used in the experiments for different model architectures (MDEQ-SMALL, MDEQ-LARGE) on the CIFAR-10 and ImageNet datasets. It specifies the input image size, the type of residual block used (BASIC or BOTTLENECK), the number of branches in the multi-resolution architecture, the number of channels at each resolution level, the number of head channels, and the final channel size.

This table presents an ablation study to investigate the impact of Jacobian regularization on the performance of MDEQ and SRS-MDEQ models on the CIFAR-10 dataset. It compares the certified accuracy for different radius values (0.0 to 1.5) using the MDEQ-30A model with and without Jacobian regularization, and also with its SRS-MDEQ-3A counterpart. This helps to understand whether Jacobian regularization is a necessary component of the proposed approach or if it can be removed without significantly affecting performance.

This table details the training hyperparameters used in the experiments described in the paper. It includes settings for batch size, epochs, optimizer, learning rate, learning rate schedule, momentum, weight decay, Jacobian regularization strength, and Jacobian regularization frequency. These parameters were used to train the MDEQ (Multi-resolution Deep Equilibrium Model) models on CIFAR-10 and ImageNet datasets. Different parameter settings are shown for the different model sizes (SMALL and LARGE) and datasets used.

This table compares the certified accuracy of the proposed Serialized Randomized Smoothing (SRS)-based Deep Equilibrium Model (DEQ) with existing methods such as Lipschitz Bound and existing randomized smoothing methods on the CIFAR-10 dataset. Different certified radii (r) are used for comparison. The results show that SRS-MDEQ achieves better certified accuracy compared to other methods.

This table shows the certified accuracy for the MDEQ-LARGE model on the CIFAR-10 dataset using different certified radii and a noise level (σ) of 0.12. It compares the certified accuracy of the standard MDEQ model against the proposed SRS-MDEQ model with varying numbers of layers (1, 3, and 5) and solvers (Naive and Anderson). The best certified accuracy is highlighted in bold for each radius.
This table shows the certified accuracy and running time for different models on the CIFAR-10 dataset using the MDEQ-LARGE architecture with varying radii. The certified accuracy represents the percentage of test images correctly classified and certified within a specified radius, while the running time indicates the computational cost for certifying a single image. The best certified accuracies for each radius are highlighted in bold. The time taken by the MDEQ-30A model is used as a baseline to compare the computational efficiency of other models.

This table presents a comparison of the certified accuracy and running time for different model architectures on the CIFAR-10 dataset using the MDEQ-LARGE model. The certified accuracy is shown for various radii (distances from the original data point), and the running time is presented relative to a baseline model (MDEQ-30A). The table showcases the performance of both the standard MDEQ and the proposed SRS-MDEQ approaches, highlighting the trade-off between accuracy and computational efficiency.

This table presents a comparison of the certified accuracy and computation time for various models on the CIFAR-10 dataset. It contrasts the performance of standard MDEQ models (with varying numbers of layers) against the proposed SRS-MDEQ models. The comparison highlights the significant speedup achieved by the SRS-MDEQ method without sacrificing much certified accuracy. The time improvement is shown relative to the MDEQ-30A model.

This table presents the certified accuracy and running time for different models on the CIFAR-10 dataset using the MDEQ-LARGE architecture. It compares the standard MDEQ with different numbers of layers (1, 5, and 30) against the proposed SRS-MDEQ method with various numbers of layers and solvers (N and A). The best certified accuracy for each radius is highlighted in bold, and the running time for each model is shown relative to the MDEQ-30A model. This comparison demonstrates the significant speedup achieved by the SRS-MDEQ method with minimal impact on accuracy.
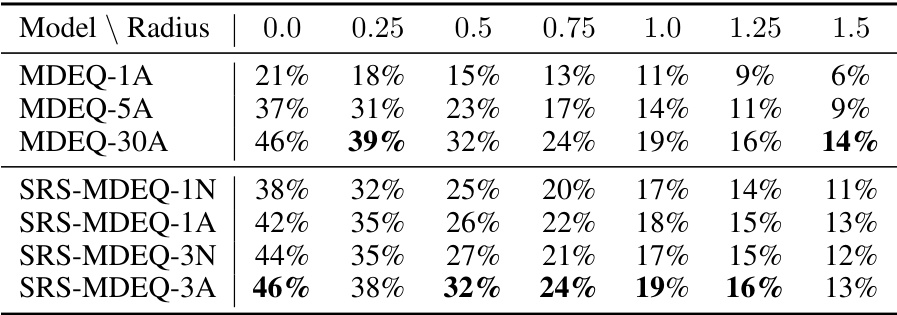
This table presents a comparison of the certified accuracy and computational time for different model configurations on the CIFAR-10 dataset, focusing on the MDEQ-SMALL architecture. The results are broken down by the certified radius (0.0 to 1.5). The best certified accuracy for each radius is highlighted in bold. The computational time is also presented, providing a relative speedup factor compared to a baseline MDEQ-30A model.
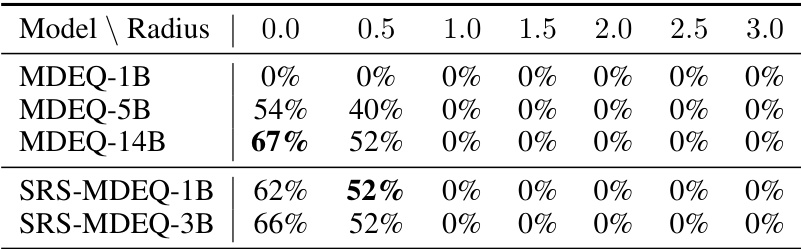
This table shows the certified accuracy and running time for different radius values for MDEQ-SMALL model on ImageNet dataset. The results are compared against a baseline (MDEQ-14B). The best accuracy for each radius is highlighted in bold, providing a direct comparison of the proposed method (SRS-MDEQ) with the baseline model across various layers (depth) and solvers, showcasing improvements in speed without significant accuracy loss.

This table presents the certified accuracy and running time for different models on ImageNet dataset. The best certified accuracy for each radius is highlighted in bold. The time taken for each model is also given and compared to MDEQ-14B as a baseline.
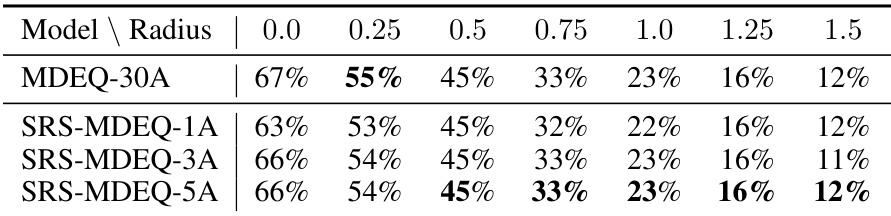
This table presents a comparison of certified accuracy and running time for different models on the CIFAR-10 dataset using the MDEQ-LARGE architecture. It shows the certified accuracy (ACR) at different certified radii (0.0 to 1.5) for several models: MDEQ-1A, MDEQ-5A, MDEQ-30A, SRS-MDEQ-1N, SRS-MDEQ-1A, and SRS-MDEQ-3A. The best certified accuracy for each radius is highlighted in bold. Additionally, the table compares the running time of each model to that of MDEQ-30A, showing the speedup achieved by the Serialized Randomized Smoothing (SRS) method.

This table presents the certified accuracy and running time for different model configurations (MDEQ-1A, MDEQ-5A, MDEQ-30A, SRS-MDEQ-1N, SRS-MDEQ-1A, SRS-MDEQ-3A) on the CIFAR-10 dataset. The results are shown for various certified radii (0.0, 0.25, 0.5, 0.75, 1.0, 1.25, 1.5). The best certified accuracy for each radius is highlighted in bold. Running times are given relative to MDEQ-30A to demonstrate the speedup achieved by the Serialized Randomized Smoothing (SRS) approach.

This table presents the certified accuracy and running time for different models on the ImageNet dataset. The models are compared based on their certified accuracy with varying radii and the running time for each model. The best certified accuracy for each radius is highlighted in bold. The running times are presented relative to the baseline model MDEQ-14B, allowing for a direct comparison of the efficiency of different models.
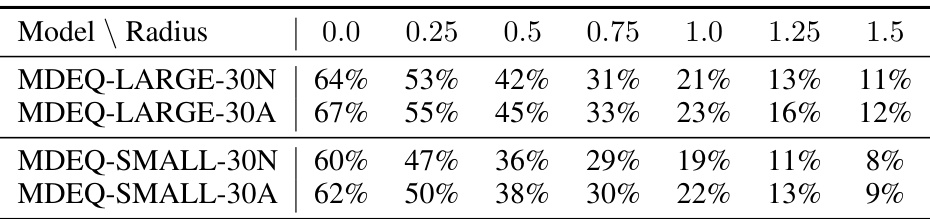
This table presents the certified accuracy results for the MDEQ-SMALL architecture on CIFAR-10, comparing the performance of different fixed-point solvers (Naive and Anderson) with varying numbers of layers (30). The results highlight the impact of the solver choice on the model’s certified robustness.
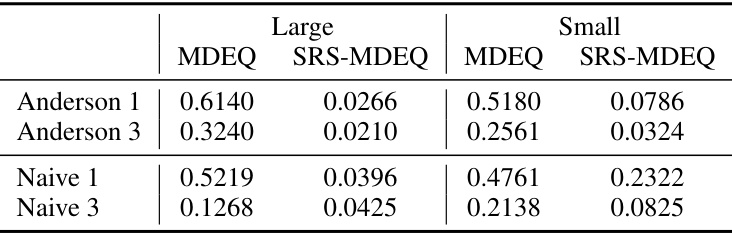
This table presents the mean Relative Radius Difference (RRD) values calculated for various solver configurations (Anderson and Naive solvers, with 1 and 3 steps). The RRD metric quantifies the difference between the certified radius produced by the proposed Serialized Randomized Smoothing (SRS) method and the accurate radius obtained from a standard DEQ for each image. Lower RRD values indicate better agreement between the SRS and DEQ certified radii, thereby suggesting the efficacy of the proposed SRS approach. The results are separately shown for MDEQ-SMALL and MDEQ-LARGE models to illustrate the effect of model size on the RRD.

This table compares the certified accuracy of the proposed Serialized Randomized Smoothing (SRS)-MDEQ method with existing methods such as SLL (Lipschitz Bound) and LBEN (Lipschitz Bound) across various certified radii (r). The best certified accuracy for each radius is highlighted in bold. The table shows that SRS-MDEQ outperforms the existing methods in terms of certified accuracy.

This table presents the certified accuracy results for the MDEQ-LARGE architecture on the CIFAR-10 dataset using a noise level (σ) of 0.5. The results are broken down by certified radius and whether the model’s initialization started from clean data or the previous fixed-point solution from a previous noisy sample. Comparing the results reveals the impact of using the previous solution as initialization in the Serialized Randomized Smoothing method.
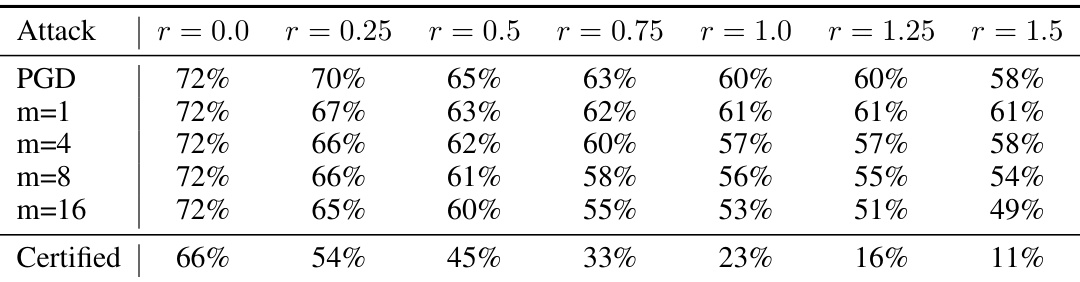
This table presents the empirical robustness of the LARGE-SRS-MDEQ-3A model against the Projected Gradient Descent (PGD) attack and its smoothed variant, Smooth-PGD. It shows the accuracy of the model under different attack strengths (m) and certified radii. The certified accuracy represents the theoretically guaranteed robustness, while the other rows demonstrate the empirical robustness against different attack strategies.

This table presents the empirical robustness results of the SMALL-SRS-MDEQ-3A model against the Projected Gradient Descent (PGD) attack and its smoothed variant, Smooth-PGD, with different perturbation magnitudes (r). The ‘Certified’ row indicates the theoretically guaranteed robustness from the randomized smoothing method, while the other rows show the empirical accuracy under different PGD attacks with varying numbers of iterations (m). The results demonstrate the model’s robustness against these attacks, with the empirical accuracy consistently above the certified level for most radii.
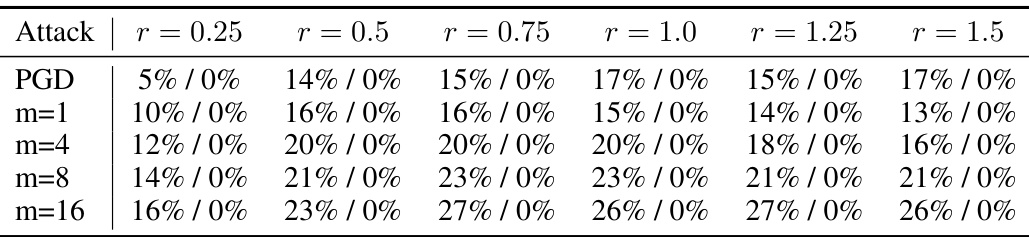
This table presents the results of point-wise successful attack rates on the LARGE-SRS-MDEQ-3A model under different attack methods and radii. For each radius and attack method, the table shows two numbers: the first is the percentage of uncertified points successfully attacked, while the second represents the percentage of certified points successfully attacked. The results indicate that even with stronger attacks, none of the certified points were successfully attacked.

This table presents the empirical robustness results of the SMALL-SRS-MDEQ-3A model against PGD and Smooth-PGD attacks. The certified accuracy represents the theoretical guarantee of robustness, while the attack success rates (under various PGD parameters ’m’) show the model’s resilience against different attack strengths. The results indicate that even stronger attacks (higher ’m’) fail to breach the certified robustness.
Full paper#