↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat
TL;DR#
Transformers heavily rely on Adam optimizer, while SGD, a standard for CNNs, performs poorly on them. This paper investigates why. Existing explanations, such as heavy-tailed noise, are insufficient. The key problem lies in the architectural differences between CNNs and Transformers, leading to different Hessian matrix properties. CNNs show homogeneity across parameter blocks, while Transformers exhibit significant ‘block heterogeneity’.
The study employs numerical linear algebra techniques, analyzing blockwise Hessian spectra of various models. Results reveal that SGD underperforms Adam precisely when this block heterogeneity exists. A novel quantitative metric (JSº) is proposed to predict SGD’s behavior, opening a new avenue for improved optimization algorithm design.
Key Takeaways#
Why does it matter?#
This paper is crucial because it sheds light on the underperformance of SGD in Transformer training, a critical issue in deep learning. It introduces the concept of block heterogeneity in the Hessian matrix, offering a novel perspective on optimizer choice. This opens avenues for improving training efficiency and designing better optimization algorithms for Transformers and potentially other deep neural network architectures.
Visual Insights#

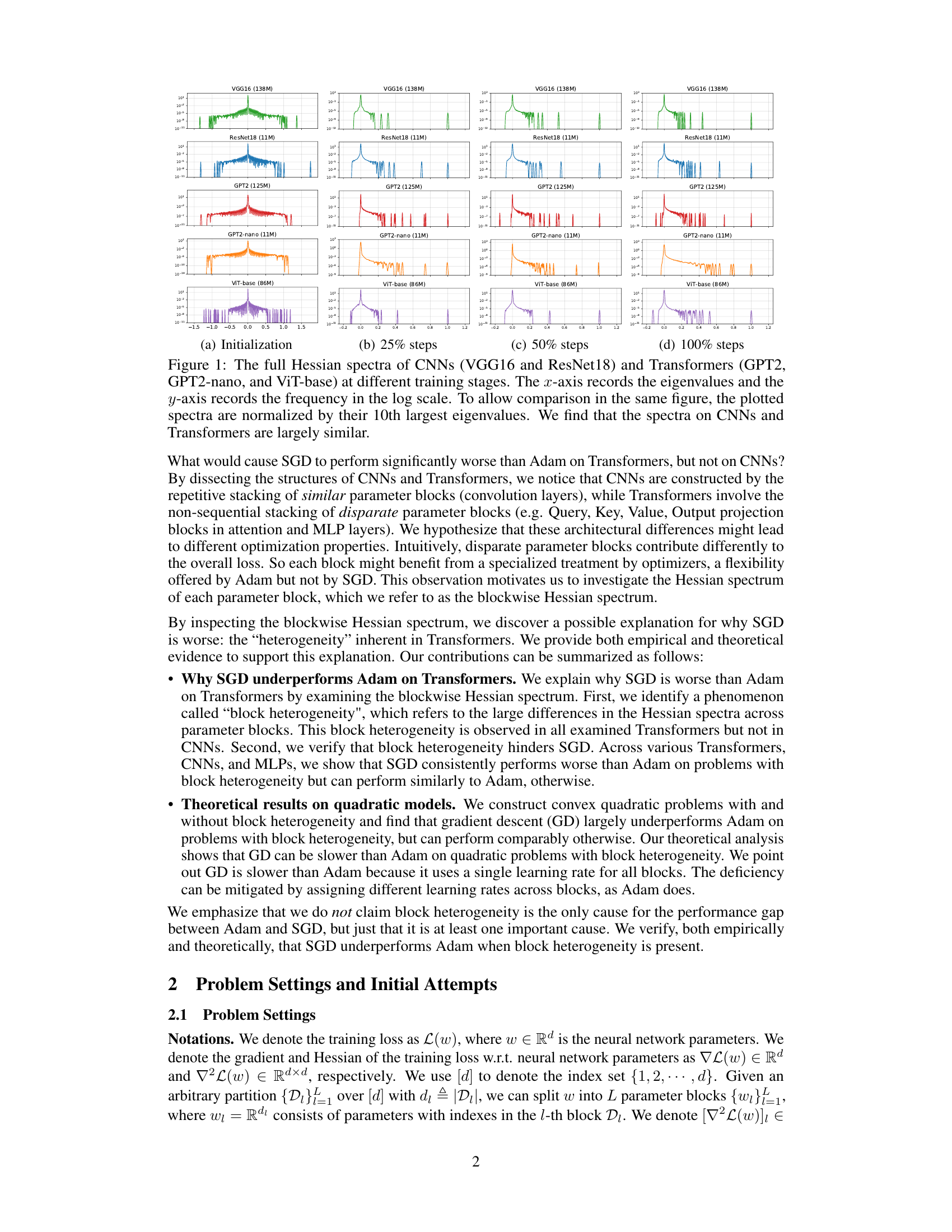
This figure displays the full Hessian spectra of several Convolutional Neural Networks (CNNs) and Transformers at various training stages. The spectra are represented as log-scaled histograms, where the x-axis shows eigenvalues and the y-axis shows their frequency. To facilitate comparison, all spectra are normalized by their 10th largest eigenvalue. The figure’s key observation is that the spectra of CNNs and Transformers are remarkably similar, despite the significant differences in training performance between Adam and SGD optimizers for these network types.

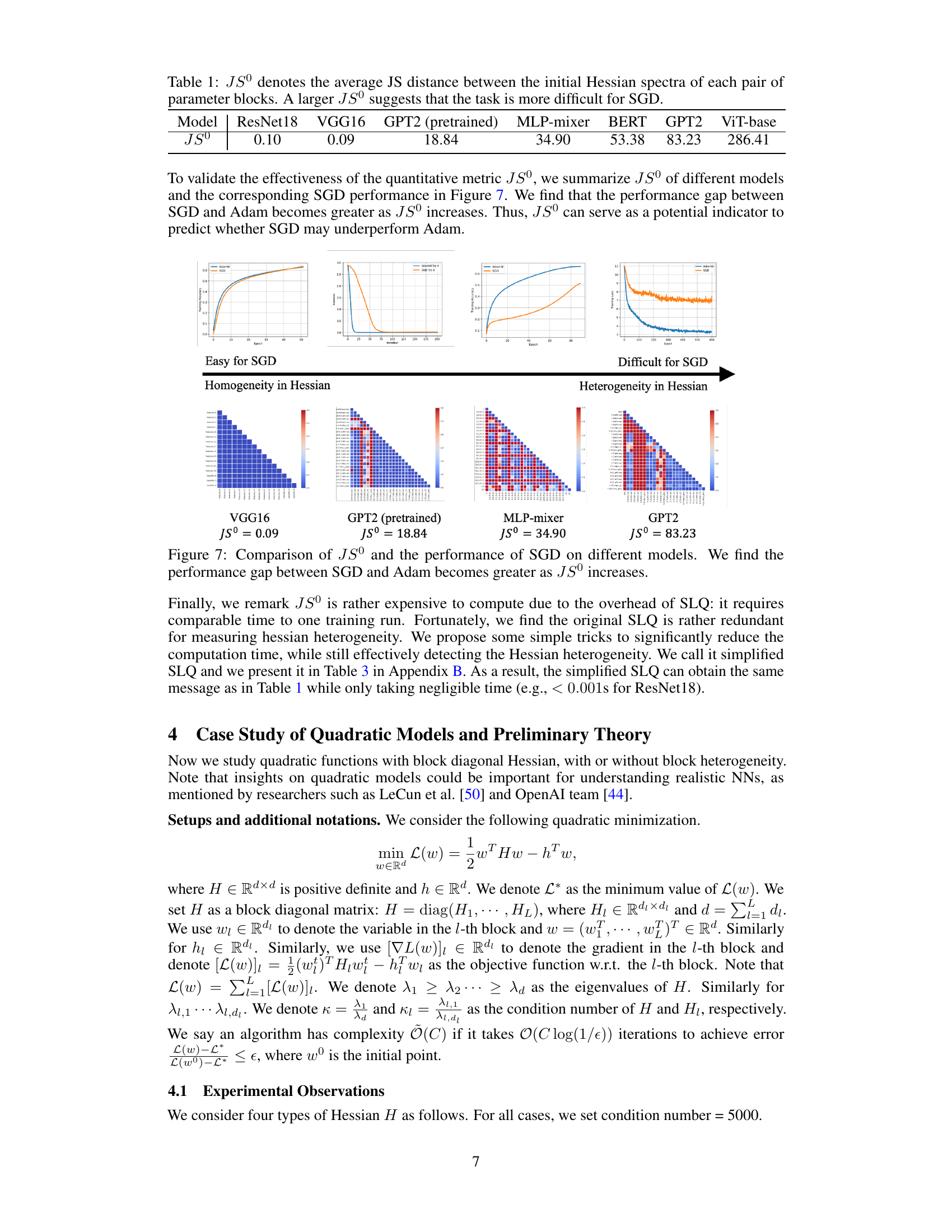
This table presents the average Jensen-Shannon (JS) distance between the initial Hessian spectra of all pairs of parameter blocks for various neural network models. The JS distance quantifies the dissimilarity in the eigenvalue distributions of the blockwise Hessians. A higher JS distance indicates greater heterogeneity (variability) in the Hessian spectra across different blocks within a model. The models include CNNs (ResNet18, VGG16), and Transformers (GPT2 (pretrained), MLP-mixer, BERT, GPT2, ViT-base). The table suggests that a higher JS distance correlates with greater difficulty in training the model using SGD, highlighting the relationship between Hessian heterogeneity and SGD performance.
In-depth insights#
Hessian Spectrum#
The Hessian spectrum, representing the eigenvalues of the Hessian matrix, offers crucial insights into the optimization landscape of neural networks. In the context of Transformers, the paper explores the blockwise Hessian spectrum, examining the eigenvalues within individual parameter blocks (like attention layers) rather than considering the entire network. This granular analysis reveals significant heterogeneity, where different blocks exhibit drastically different eigenvalue distributions. This block heterogeneity is identified as a key factor hindering the performance of SGD, an optimizer that employs a single learning rate for all parameters, while Adam, with its adaptive learning rates, effectively manages this heterogeneity. The paper’s findings suggest that blockwise spectral analysis provides more informative insights than examining the full Hessian spectrum, allowing a deeper understanding of the performance differences between optimizers on Transformers versus CNNs. Finally, the implications of the blockwise heterogeneity on the choice of optimizer are thoroughly discussed.
Adam vs. SGD#
The comparative analysis of Adam and SGD optimizers reveals Adam’s superior performance, especially in training large transformer models. While SGD, a classic optimizer, struggles with the inherent heterogeneity of transformer architectures, Adam’s adaptive learning rate mechanism effectively handles the varied Hessian spectra across different parameter blocks. This results in faster convergence and better overall performance for Adam. The paper identifies ‘block heterogeneity’ as a critical factor contributing to this performance gap. While the full Hessian spectrum reveals minimal differences between CNNs (where SGD performs well) and transformers, analyzing the blockwise Hessian spectra reveals significant differences in the eigenvalue distributions within the blocks, thus explaining the contrast in optimizer effectiveness. This is further validated through theoretical analysis on quadratic models, which demonstrates the limitation of SGD’s uniform learning rate approach compared to Adam’s adaptive learning rates. The research highlights the potential of blockwise Hessian analysis to guide optimizer selection and provide a more nuanced understanding of neural network training dynamics.
Block Heterogeneity#
The concept of “Block Heterogeneity” in the context of the provided research paper centers on the variability of Hessian spectra across different parameter blocks within a neural network, particularly prominent in Transformer architectures. This heterogeneity contrasts with the more homogeneous spectra observed in CNNs. The authors posit that this disparity in Hessian characteristics significantly impacts the performance of optimizers. Specifically, SGD struggles with block heterogeneity, as its single learning rate fails to effectively adapt to the varying curvature across blocks, resulting in suboptimal convergence. In contrast, Adam’s adaptive learning rate mechanism mitigates this issue, allowing for better performance in the face of diverse Hessian landscapes. The paper demonstrates that this phenomenon is not solely limited to Transformers, suggesting that block heterogeneity is a more general property influencing optimizer choice. The findings imply that future research may benefit from explicitly considering this factor in the design and optimization of neural networks.
Quadratic Analysis#
A quadratic analysis in the context of a research paper on optimizers for neural networks would likely involve simplifying the complex, high-dimensional loss landscape into a more manageable quadratic model. This allows for a more tractable theoretical analysis of optimizer behavior, particularly concerning the impact of Hessian properties like block heterogeneity and eigenvalue distribution. By studying the convergence of gradient descent and Adam on such quadratic models with varying Hessian structures, researchers can gain valuable insights into why Adam outperforms SGD for training Transformers, potentially isolating the effect of Hessian block heterogeneity as a key factor. Key findings might demonstrate that while SGD struggles with heterogeneous blocks due to its single learning rate, Adam’s coordinate-wise learning rates effectively handle this heterogeneity. The quadratic analysis can provide a foundational understanding that supports empirical observations in more realistic scenarios. However, it’s crucial to acknowledge that the quadratic approximation is a simplification and the conclusions must be carefully extrapolated to the true non-convex landscape of deep learning models. The main strength lies in its ability to isolate and examine the effect of Hessian structure on optimizer convergence, providing a clearer mechanistic understanding than is achievable with only empirical results.
Future Work#
The paper’s lack of a dedicated ‘Future Work’ section is notable. However, several avenues for future research emerge from the study’s conclusions. Investigating the interplay between block heterogeneity and other phenomena impacting Transformer training (e.g., gradient vanishing/explosion, layer normalization) is crucial. Developing refined theoretical models that move beyond quadratic approximations and incorporate the complexities of deep learning architectures would significantly strengthen the work’s implications. Further, exploring the efficacy of different learning rate scheduling strategies, especially in conjunction with pre-training and fine-tuning, would provide valuable insights. Finally, extending the analysis to encompass a broader range of architectures and tasks, beyond the selected Transformers, CNNs, and MLPs, is essential for generalizing the findings. The study’s robust empirical results provide a solid foundation for these future inquiries.
More visual insights#
More on figures

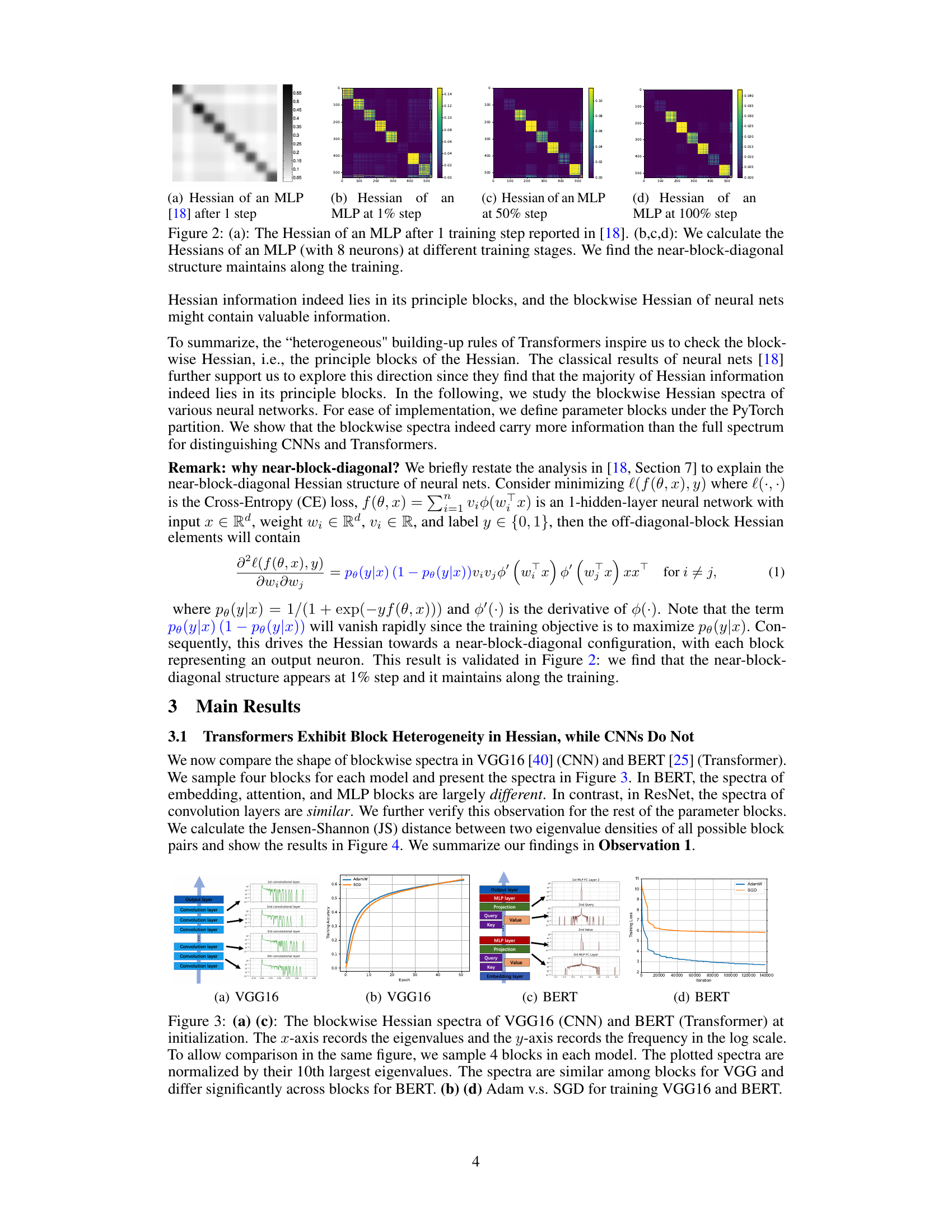
This figure shows the Hessian matrices of a Multilayer Perceptron (MLP) with 8 neurons at different training stages. Subfigure (a) is reproduced from a previous work [18], showing the Hessian after only 1 training step. Subfigures (b), (c), and (d) show the Hessians calculated by the authors of the current paper at 1%, 50%, and 100% of training, respectively. The visualization highlights the near-block-diagonal structure of the Hessian, which remains consistent throughout the training process. This structure is important because it suggests that the Hessian information is concentrated in its principal blocks (i.e., block-diagonal elements are much larger than off-diagonal elements).
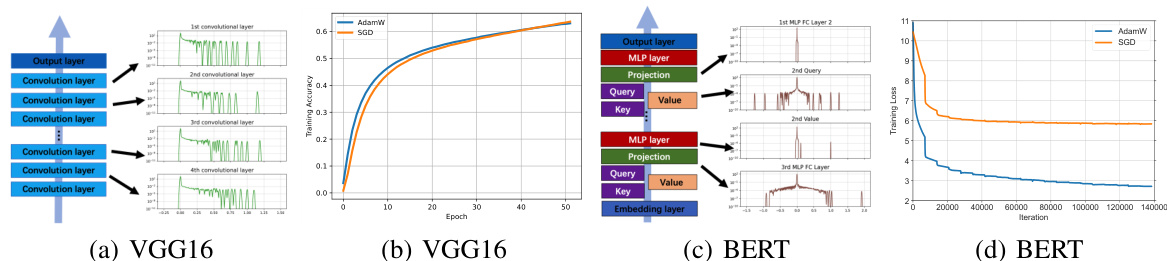
This figure compares the blockwise Hessian spectra of a CNN (VGG16) and a Transformer (BERT) at the initialization stage. The blockwise Hessian spectrum shows the distribution of eigenvalues within individual parameter blocks (e.g., convolutional layers in CNNs, attention and MLP layers in Transformers). The figure highlights the key difference between CNNs and Transformers: CNNs exhibit homogeneity (similar spectra across blocks), whereas Transformers show significant heterogeneity (very different spectra across blocks). This heterogeneity in Transformers is linked to the performance difference between SGD and Adam optimizers: SGD struggles with the heterogeneous spectra of Transformers, while performing comparably to Adam in homogeneous cases such as CNNs. The training loss curves for both models with Adam and SGD are also shown, illustrating the performance gap.
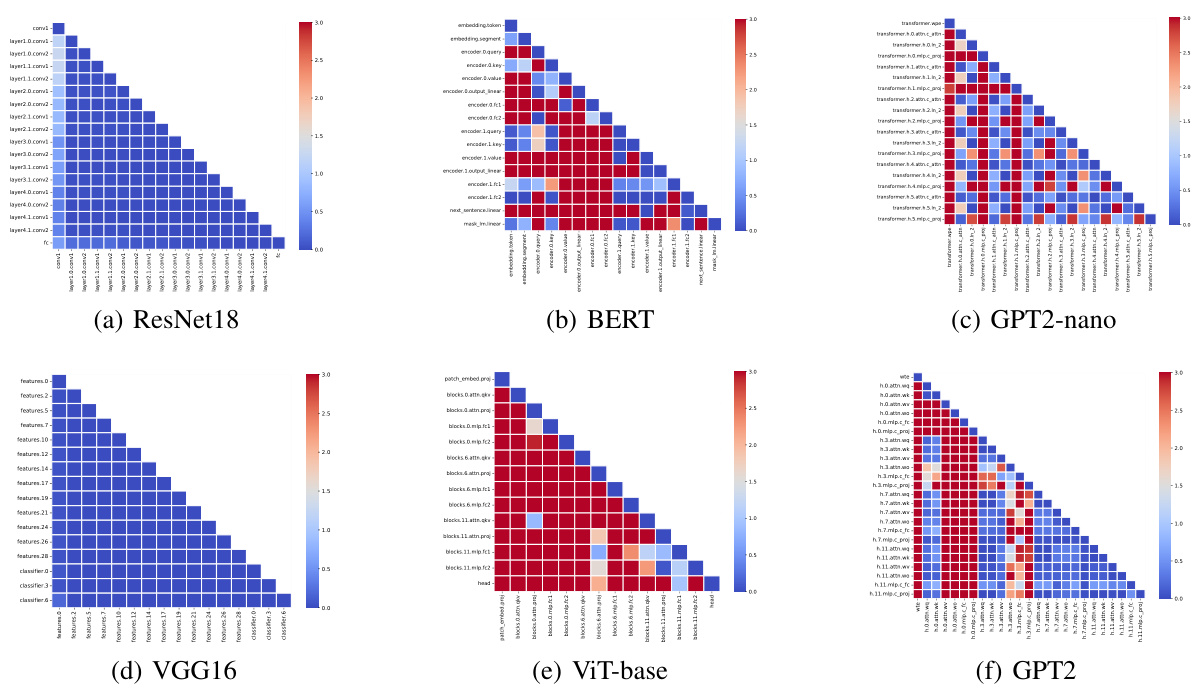
This figure visualizes the Jensen-Shannon (JS) distance between the blockwise Hessian spectra at initialization for various CNNs and Transformers. The JS distance measures the similarity between two probability distributions. Lower JS distance indicates higher similarity. The heatmap shows that CNNs (ResNet18, VGG16) exhibit much smaller JS distances, indicating high similarity between their blockwise Hessian spectra, whereas Transformers (BERT, GPT2-nano, ViT-base, GPT2) show significantly larger JS distances, indicating substantial heterogeneity (dissimilarity) in their blockwise Hessian spectra.
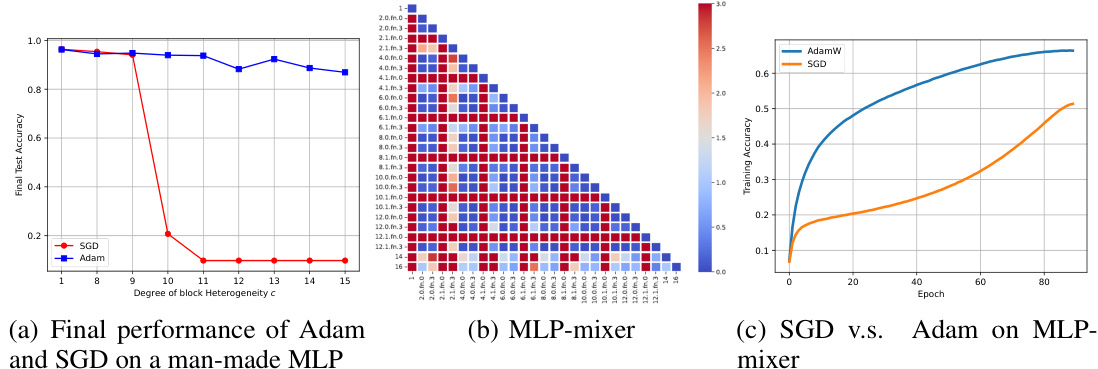
This figure presents a comparison of Adam and SGD optimizers on three different scenarios: (a) A man-made MLP with varying degrees of block heterogeneity, (b) MLP-mixer architecture at initialization, and (c) Training curves of Adam and SGD for MLP-mixer. The results show that SGD consistently underperforms Adam when block heterogeneity is present. This highlights the importance of Adam’s ability to handle the heterogeneity in the Hessian spectra across different parameter blocks, which SGD lacks.

This figure shows the results of fine-tuning a pre-trained GPT2 model on the Alpaca Eval dataset. The left panel (a) displays the Jensen-Shannon (JS) distance among blockwise Hessian spectra at initialization, illustrating the degree of heterogeneity (differences) in the Hessian among parameter blocks. The right panel (b) presents the training loss curves for both SGD and Adam optimizers, demonstrating the relative performance difference between these optimizers in this specific setting, where pre-training has already partially mitigated block heterogeneity.
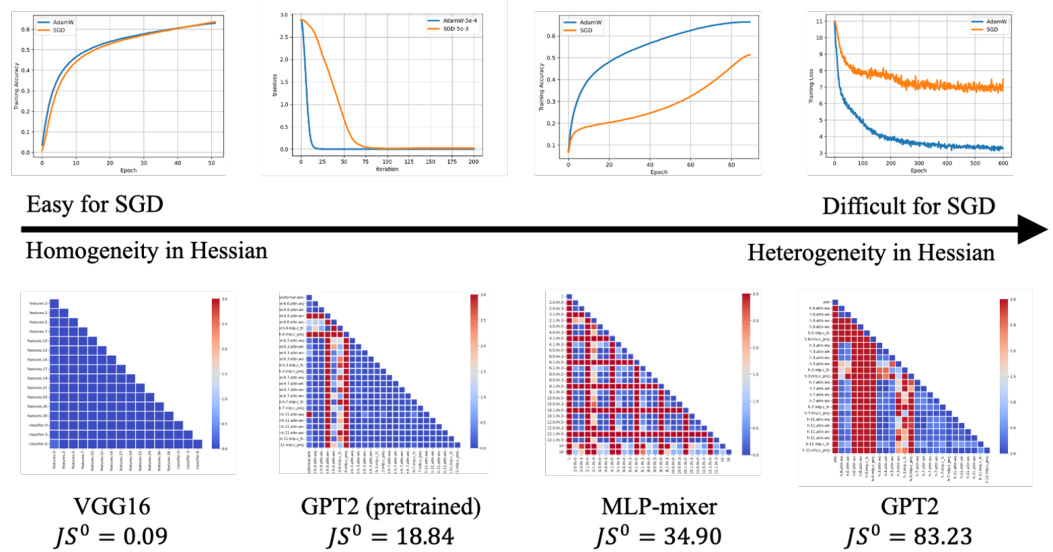
This figure compares the averaged Jensen-Shannon (JS) distance among blockwise Hessian spectra at initialization (JSº) with the performance difference between Adam and SGD for various models. The results show a clear correlation: as JSº increases (indicating greater heterogeneity in the Hessian), SGD performs significantly worse compared to Adam. This supports the paper’s claim that block heterogeneity in the Hessian is a key factor determining SGD’s performance compared to Adam.

This figure shows the performance comparison between Adam and Gradient Descent (GD) on four different types of quadratic problems, each with a condition number of 5000. The problems are designed to have either homogeneous or heterogeneous Hessian blockwise spectra. The plots display the log of the gradient norm against the number of iterations. The results demonstrate that GD performs significantly worse than Adam when the Hessian exhibits block heterogeneity (Cases 1 and 3). However, when the blockwise Hessian is homogeneous (Cases 2 and 4), GD’s performance is similar to Adam’s.

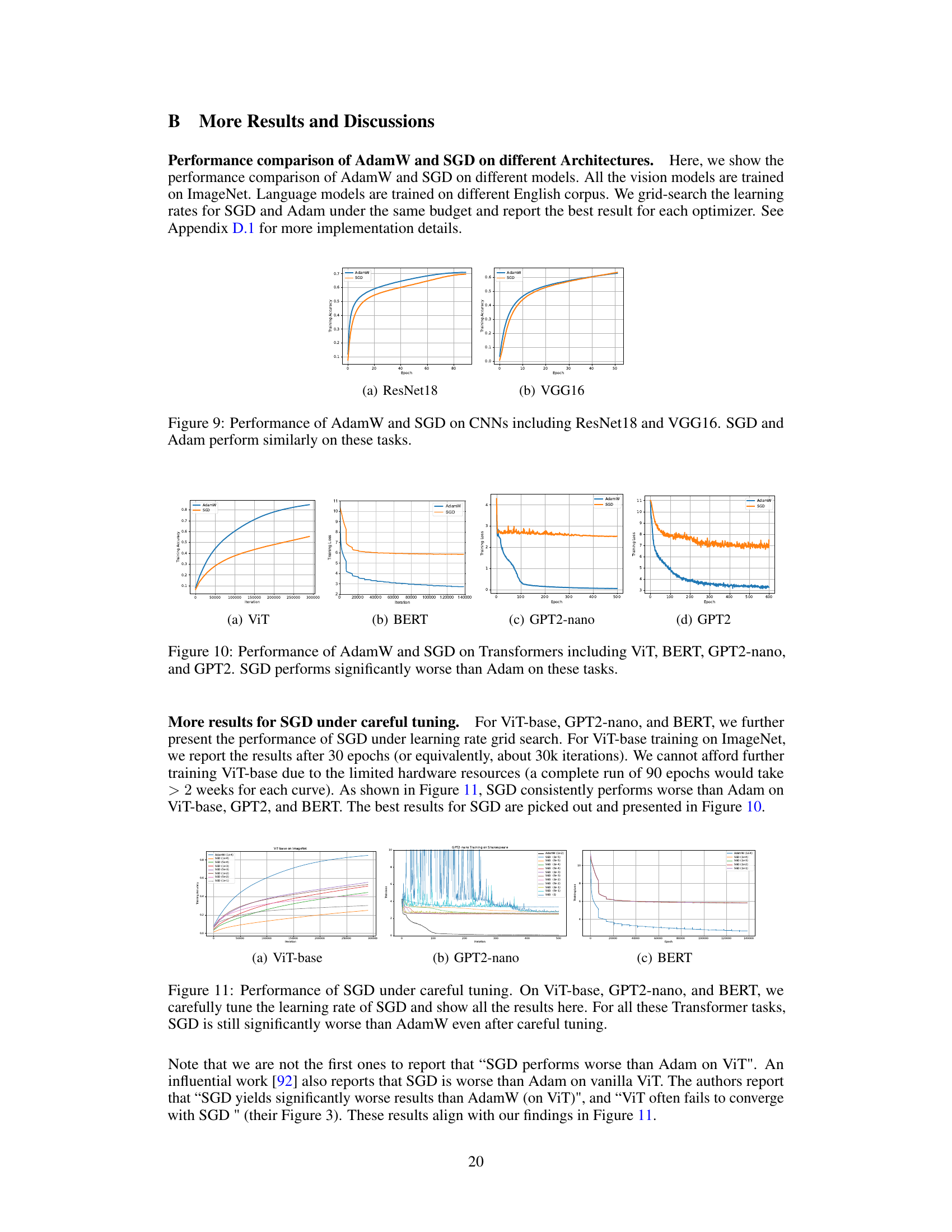
This figure compares the training accuracy of AdamW and SGD optimizers on two Convolutional Neural Networks (CNNs): ResNet18 and VGG16. The results show that both optimizers achieve comparable performance on these CNN architectures, indicating that the significant performance gap observed between Adam and SGD in Transformers does not extend to all network architectures.
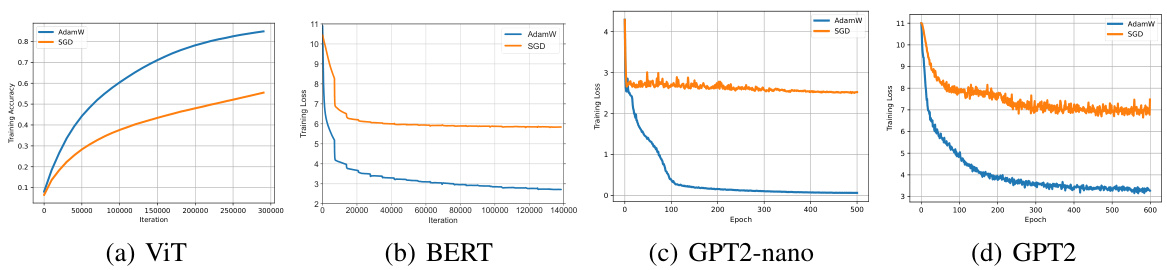
This figure shows the comparison of AdamW and SGD optimizers on four different transformer models: ViT, BERT, GPT2-nano, and GPT2. The training performance is evaluated for each model and optimizer using training loss and accuracy as metrics. The results clearly demonstrate that AdamW consistently outperforms SGD across all four transformer architectures, indicating a significant performance gap between the two optimizers.
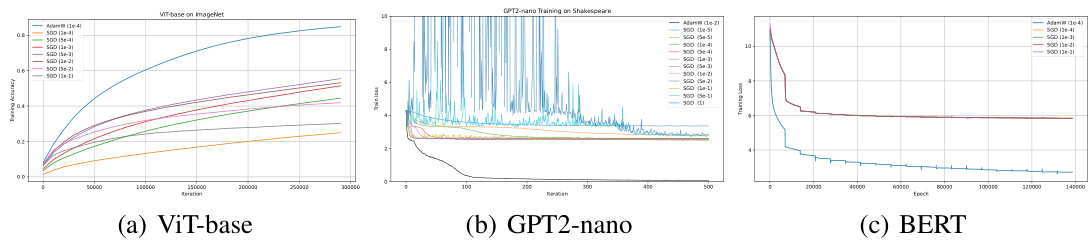
This figure compares the performance of AdamW and SGD optimizers on various Transformer models (ViT, BERT, GPT2-nano, and GPT2) during training. The x-axis represents the training iterations or epochs, and the y-axis shows the training loss or accuracy. The results demonstrate that AdamW consistently outperforms SGD across all the Transformer models tested, highlighting a significant performance gap. This observation underscores the central theme of the paper, which investigates why Adam is preferred over SGD for training Transformers.

This figure compares the blockwise Hessian spectra of a CNN (VGG16) and a Transformer (BERT) at the initialization stage. The x-axis represents the eigenvalues of the Hessian, and the y-axis represents their frequency (on a logarithmic scale). Four representative blocks are selected for each model. The normalization of the spectra allows for a direct comparison within the figure. The key observation is the difference in spectral similarity between the blocks in the CNN and the Transformer. In VGG16, the spectra are very similar across the blocks while, in BERT, the spectra are quite different. This difference illustrates the ‘block heterogeneity’ present in transformers, a key aspect investigated in this paper.
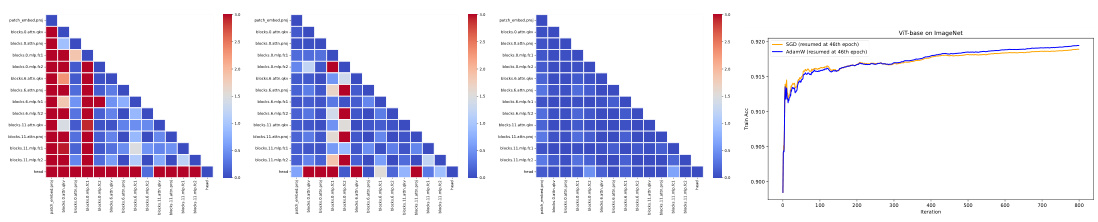
This figure visualizes the Jensen-Shannon (JS) distance between the blockwise Hessian spectra at initialization for various CNNs and Transformers. The heatmap shows the pairwise JS distance between all pairs of blocks within each model. The key observation is that the JS distance is significantly smaller for CNNs compared to Transformers, indicating a greater heterogeneity in the Hessian spectra across blocks within Transformers.

This figure shows the histograms of eigenvalues for four blocks in a heterogeneous Hessian matrix (Case 1). The eigenvalues are sampled from different layers of the GPT2 model to represent the heterogeneous nature of Transformers. The scaling and shifting ensure strong convexity and a specific condition number (5000), while preserving the original relative range and heterogeneity of the eigenvalues across the blocks.
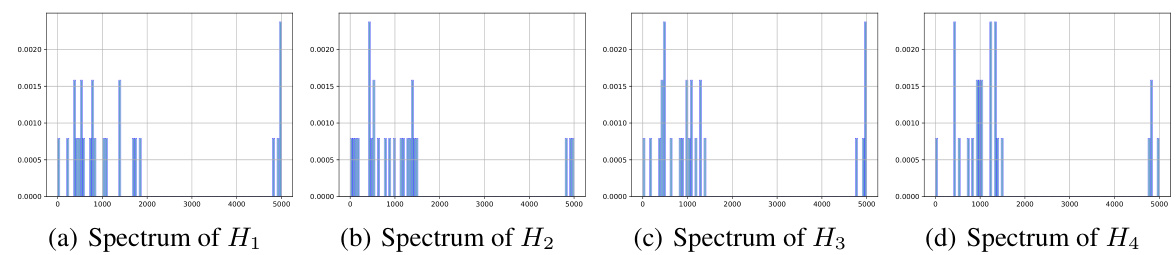
This figure compares the full Hessian spectra of Convolutional Neural Networks (CNNs) and Transformers at different training stages. The spectra are plotted on a log scale to show a wide range of eigenvalues. The authors normalized the spectra to allow for comparison across different models. The key finding is that the overall shape and distribution of eigenvalues are similar for both CNNs and Transformers, despite the significant difference in the performance of SGD on the two architectures. This suggests that examining the full Hessian spectrum alone may not be sufficient to explain the difference in optimizer performance.
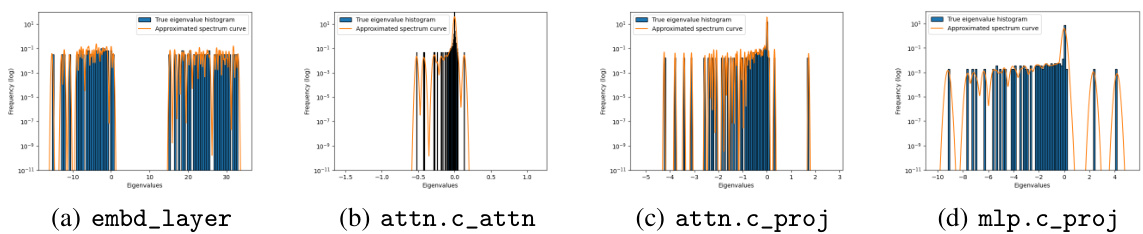
This figure compares the full Hessian spectra of Convolutional Neural Networks (CNNs) and Transformers at various training stages. The spectra, which represent the distribution of eigenvalues of the Hessian matrix, are plotted on a logarithmic scale for better visualization. The normalization by the 10th largest eigenvalue allows for direct comparison between different models. The observation that the spectra are largely similar in CNNs and Transformers despite the differences in training behavior with SGD and Adam is presented as a key finding.
Full paper#