↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Link prediction is a crucial task in graph machine learning, with numerous applications across diverse domains. While message-passing neural networks (MPNNs) are the de facto standard, their performance in link prediction often falls short compared to simple heuristics like Common Neighbors (CN). This discrepancy arises because MPNNs excel at node-level representation but struggle to capture joint structural features essential for link prediction.
This research introduces Message Passing Link Predictor (MPLP), a novel link prediction model that addresses these limitations. MPLP harnesses the orthogonality of input vectors to effectively estimate link-level structural features, including CN, while preserving the node-level complexities. Extensive experiments on benchmark datasets demonstrate that MPLP consistently outperforms existing methods, establishing new state-of-the-art results. The findings offer crucial insights into the capabilities of GNNs and pave the way for the development of more effective and efficient link prediction models.
Key Takeaways#
Why does it matter?#
This paper is crucial because it challenges the conventional wisdom in graph neural networks (GNNs) for link prediction by demonstrating that pure message passing can effectively approximate common neighbor heuristics. This opens new avenues for designing more efficient and accurate link prediction models, impacting various fields from social network analysis to knowledge graph completion. The findings also shed light on the inherent capabilities of GNNs and how they can be further improved through thoughtful architectural design and optimization.
Visual Insights#

This figure illustrates the limitations of Message Passing Neural Networks (MPNNs) in link prediction. Panel (a) shows that isomorphic nodes (nodes with the same local structure) get identical representations in MPNNs, making it difficult to distinguish between links that connect to similar nodes (e.g., (v₁, v₃) and (v₁, v₅)). Panel (b) demonstrates how MPNNs attempt to count common neighbors (CN) by using the inner product of one-hot encoded node vectors; however, this method is limited compared to the efficiency of dedicated heuristics.
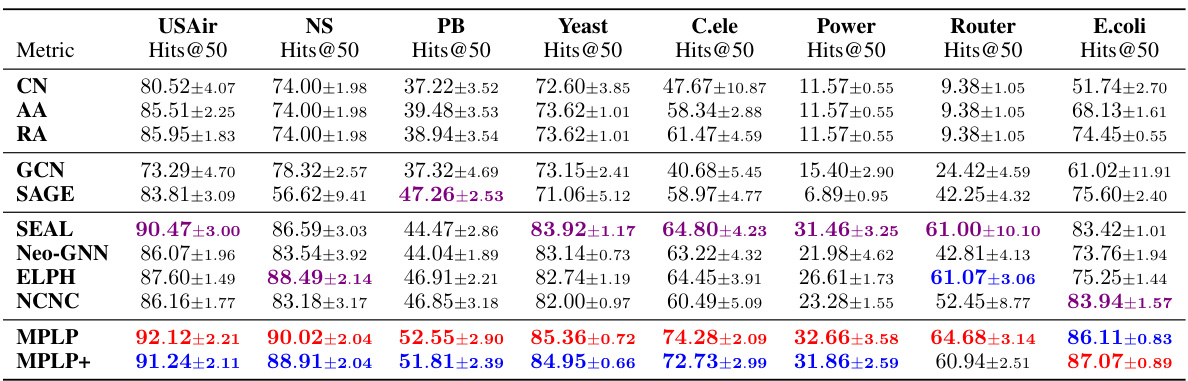
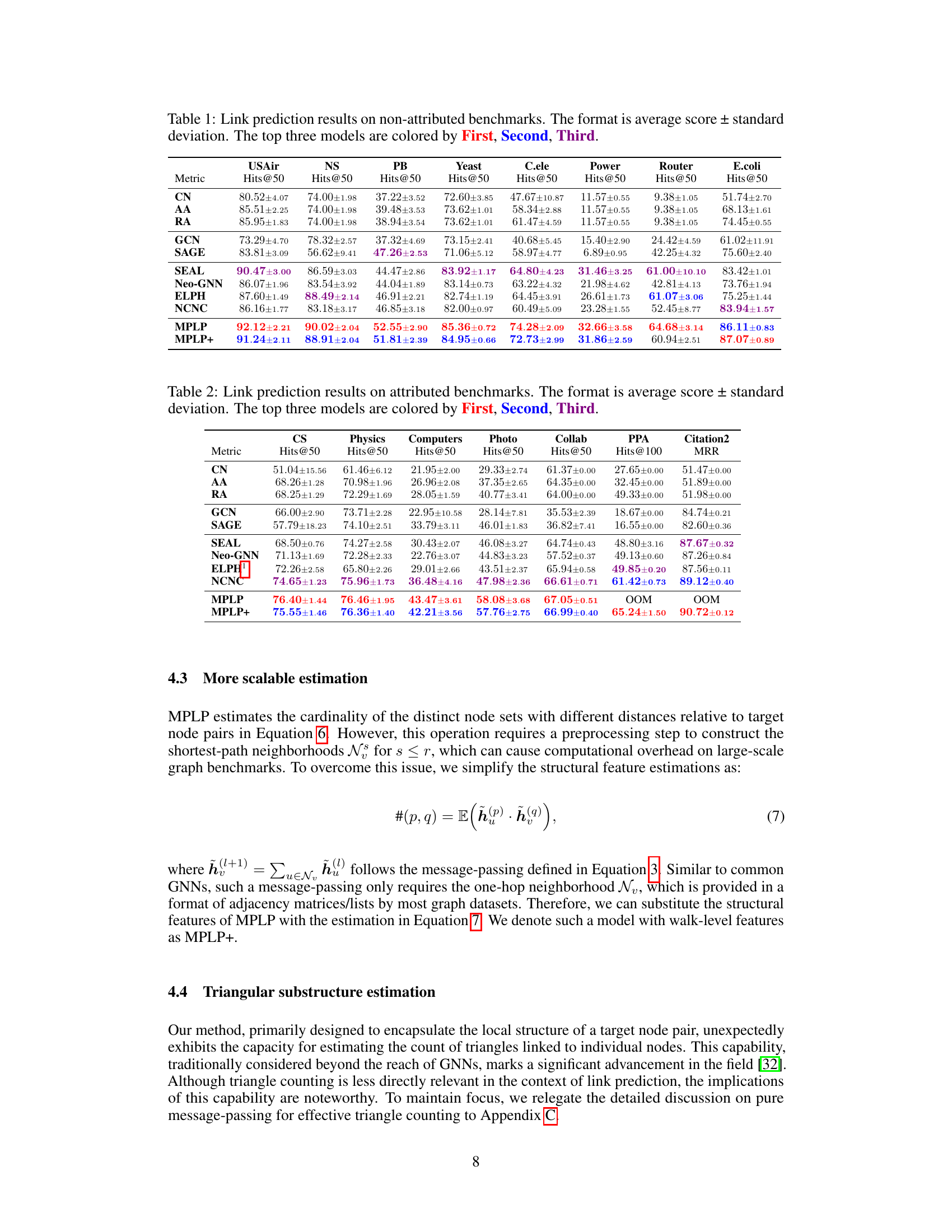
This table presents the results of link prediction experiments on eight non-attributed benchmark datasets. The performance of various models is evaluated using Hits@50, a metric that measures the percentage of correctly predicted links among the top 50 predicted links. The table compares the performance of several heuristic methods (CN, AA, RA), Graph Neural Networks (GCN, SAGE, SEAL), and the proposed methods (MPLP, MPLP+). The best-performing three models in each dataset are highlighted.
In-depth insights#
MPNN Link Prediction#
Message Passing Neural Networks (MPNNs) have shown promise in link prediction, a crucial task in graph machine learning. However, their performance isn’t always superior to simpler heuristics, like Common Neighbors. This limitation stems from MPNNs excelling at node-level representations but struggling to effectively encode joint structural features vital for link prediction. Some research suggests that by leveraging the orthogonality of input vectors, pure message passing within MPNNs can indeed capture these joint structural features, leading to improved link prediction accuracy. This approach focuses on approximating heuristic methods within the MPNN framework, rather than solely relying on node embeddings. Approaches like Message Passing Link Predictor (MPLP) exploit this orthogonality to estimate link-level structural features, such as Common Neighbors, while maintaining the efficiency of node-level operations. This highlights a potential shift in MPNN design, focusing on directly estimating joint features essential for accurate link prediction, and potentially surpassing the limitations of traditional node-centric approaches.
Quasi-Orthogonal Vectors#
The concept of “Quasi-Orthogonal Vectors” is a crucial element in the paper, offering a novel approach to link prediction. It leverages the property that in high-dimensional spaces, randomly sampled vectors tend to be nearly orthogonal. This quasi-orthogonality, while not perfect, allows the model to effectively approximate the Common Neighbors heuristic. The use of quasi-orthogonal vectors is computationally efficient compared to explicitly calculating orthogonality, making the approach scalable to large graphs. This approximation avoids the computational overhead of explicitly calculating common neighbors, which scales quadratically with the number of nodes. Furthermore, the authors highlight that the quasi-orthogonality is preserved even after message passing, enabling the model to efficiently capture structural information from the graph, crucial for accurate link prediction. By harnessing this property, the model avoids the permutation invariance limitations of traditional MPNNs, thus improving the performance in estimating structural features essential to link prediction.
MPLP Model#
The Message Passing Link Predictor (MPLP) model presents a novel approach to link prediction in graphs by directly estimating common neighbor counts using pure message passing. Unlike traditional GNNs which struggle with joint structural feature encoding, MPLP leverages quasi-orthogonal input vectors to approximate these counts efficiently, even surpassing simpler heuristic methods. The model is further enhanced by integrating node-level representations from a GNN and utilizing a distance encoding scheme to capture broader topological information. MPLP’s innovative use of quasi-orthogonal vectors and efficient message passing offers superior performance and scalability compared to existing link prediction methods, particularly in large-scale graphs, making it a significant advancement in the field. While the model shows strong potential, further research is needed to fully understand its limitations and address potential biases in the estimation of structural features.
Scalable Estimation#
Scalable estimation in link prediction focuses on efficiently handling massive graphs. Computational cost becomes a major hurdle when dealing with large datasets; thus, methods that accurately estimate link probabilities without requiring exhaustive calculations are crucial. Approaches like those based on quasi-orthogonal vectors offer a path towards scalability, allowing for approximations of complex heuristics (e.g., Common Neighbors) which are computationally expensive to compute exactly. Probabilistic methods, such as those drawing inspiration from DotHash, trade off some precision for efficiency by introducing randomness, which can be mitigated with strategies like one-hot encoding for high-degree nodes. The effectiveness of these methods rests on the characteristics of real-world graphs, like power-law distributions, that lend themselves to approximation techniques. The key is striking a balance between accuracy and speed, ensuring that estimations remain reliable while enabling efficient processing of large-scale data.
Future Directions#
Future research could explore extending the model’s capabilities to handle diverse graph types and sizes more efficiently. Investigating the impact of different aggregation functions and update mechanisms within the message-passing framework would reveal crucial insights into improving the model’s accuracy and scalability. Furthermore, exploring the integration of attention mechanisms could enhance the model’s ability to selectively focus on the most informative parts of the graph, thereby boosting its overall performance. Another important direction would be to develop more robust and unbiased estimators for structural features, reducing the variance and improving the model’s generalization capabilities. Finally, it would be beneficial to investigate the theoretical properties of the message-passing mechanism in relation to various link prediction tasks, leading to a deeper understanding of its strengths and limitations and potentially to design more efficient and effective algorithms.
More visual insights#
More on figures

This figure shows the results of an experiment where Graph Convolutional Networks (GCNs) were trained to estimate three different link prediction heuristics: Common Neighbors (CN), Adamic-Adar (AA), and Resource Allocation (RA). The mean squared error (MSE) between the GCN’s predictions and the true heuristic values is shown for eight different datasets. A baseline is also shown, which represents the MSE obtained by simply using the mean heuristic value across all links in the training set. The lower the MSE, the better the GCN is able to estimate the corresponding heuristic.
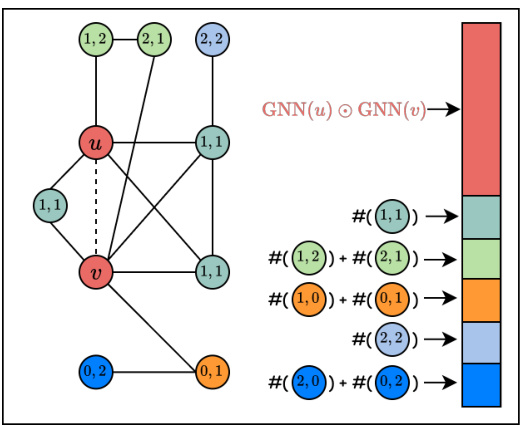
This figure illustrates the input to the Message Passing Link Predictor (MPLP) model. The nodes are color-coded according to their shortest path distance from the target link (u,v). The model uses this information to learn joint structural features of the link.
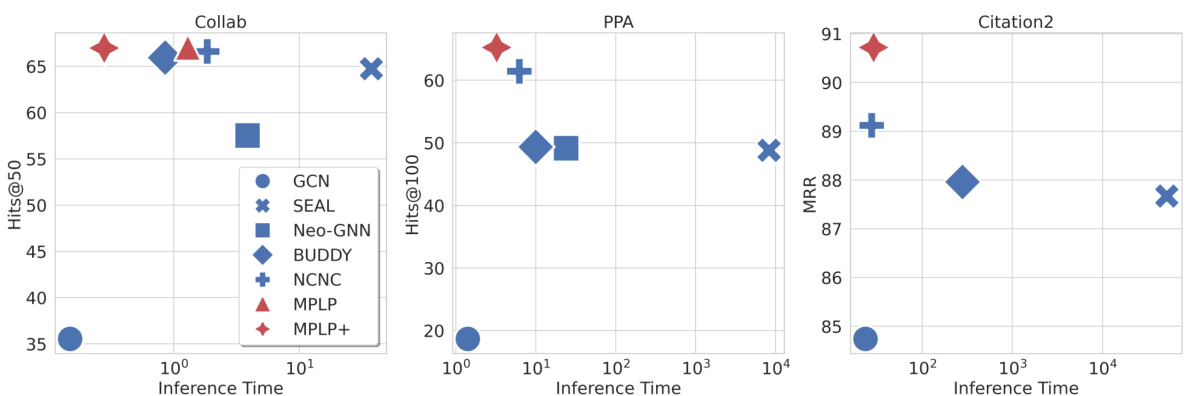
This figure evaluates the inference time of various link prediction models on three large OGB datasets (Collab, PPA, and Citation2). The x-axis represents the inference time (in seconds), while the y-axis shows the performance metric (Hits@50 for Collab, Hits@100 for PPA, and MRR for Citation2). Each point represents a different model, illustrating the trade-off between inference speed and predictive accuracy. The figure demonstrates that MPLP and MPLP+ achieve state-of-the-art performance while maintaining relatively fast inference times, especially when compared to other methods such as SEAL and Neo-GNN.
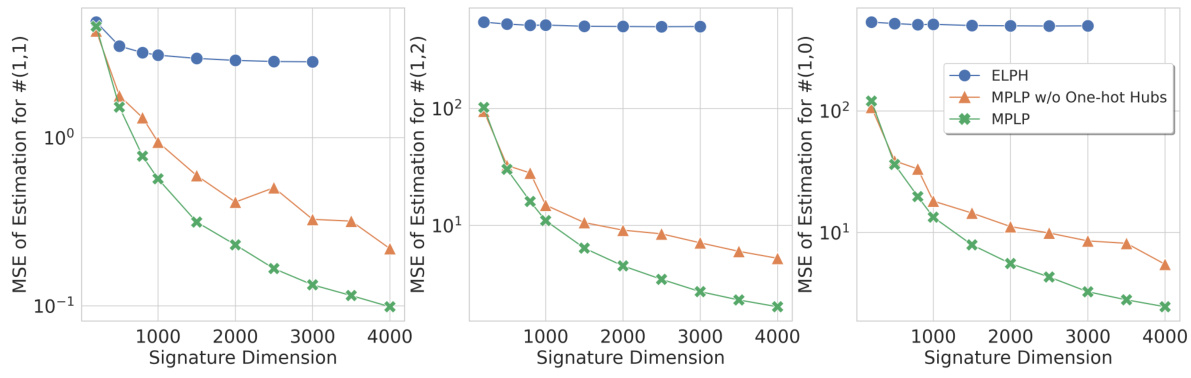
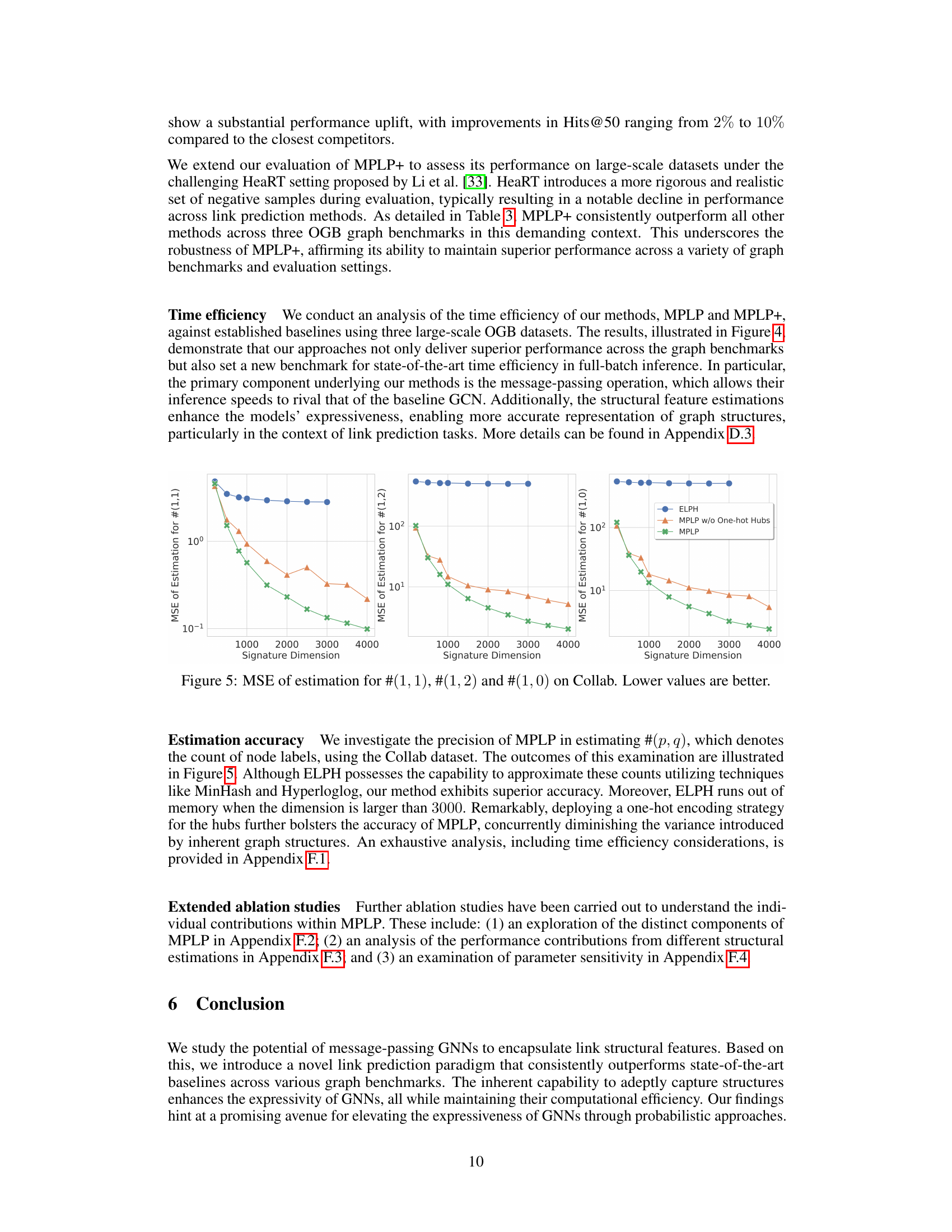
This figure displays the mean squared error (MSE) of the estimations for three different structural features: #(1,1), #(1,2), and #(1,0) on the Collab dataset. The x-axis represents the signature dimension used in the experiment, while the y-axis shows the MSE. Lower MSE values indicate better estimation accuracy. The figure compares the performance of ELPH, MPLP without One-hot Hubs, and MPLP with One-hot Hubs, demonstrating how the inclusion of One-hot Hubs improves accuracy and reduces variance.

The figure displays heatmaps showing the inner product of node attributes for three datasets: CS, Photo, and Collab. Each heatmap visualizes the pairwise inner product of node attribute vectors. The color intensity represents the magnitude of the inner product, with darker shades indicating smaller values and lighter shades indicating larger values. This visualization helps to illustrate the degree of orthogonality (or lack thereof) between the node attribute vectors in each dataset, which is relevant to the paper’s exploration of quasi-orthogonal vectors for efficient link prediction.
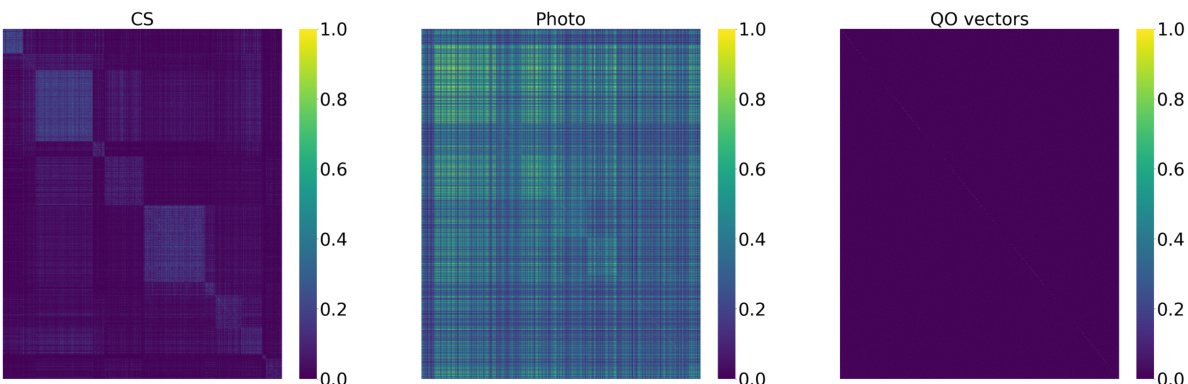
This figure presents three heatmaps visualizing the inner product of node attributes for the datasets CS and Photo, along with a heatmap showing the inner product of quasi-orthogonal (QO) vectors. The heatmaps for CS and Photo are arranged with nodes grouped by their labels, revealing the relationships between nodes with similar characteristics. The third heatmap illustrates the inner product of randomly generated QO vectors, highlighting their near-orthogonality, which is a key aspect of the proposed method in the paper.

This figure shows the mean squared error (MSE) of estimating the number of nodes with shortest path distances of (2,2) and (2,0) from the target node pair in the Collab dataset, as well as the estimation time. The results are shown for different signature dimensions (the dimensionality of the random vectors used in the model). Lower MSE values indicate better accuracy in estimating the node counts. The estimation time also increases with the signature dimension. The plot compares the performance of ELPH, MPLP without one-hot hubs, and MPLP.

This figure illustrates how the Message Passing Link Predictor (MPLP) model represents the target link (u, v). Nodes are color-coded to show their distance from u and v, allowing the model to capture the joint structural features of the link. The different colors represent the different shortest path distances from u and v to each node. This encoding allows the model to learn sophisticated representations that go beyond simple heuristics like common neighbors.
More on tables

This table presents the results of link prediction experiments on seven attributed graph datasets. The metrics used are Hits@50 for five datasets and MRR (Mean Reciprocal Rank) for the remaining two. The table compares the performance of several link prediction methods, including heuristic methods (CN, AA, RA), node-level GNNs (GCN, SAGE), link-level GNNs (SEAL, Neo-GNN, ELPH, NCNC), and the proposed method MPLP and its variant MPLP+. The top three performing methods for each dataset are highlighted.

This table presents the results of link prediction experiments conducted on three large-scale Open Graph Benchmark (OGB) datasets using the HeaRT evaluation protocol. The protocol introduces a more rigorous negative sampling strategy than previous methods. The table shows the performance of various link prediction methods, including MPLP+, measured by MRR (Mean Reciprocal Rank) and Hits@20 (the number of times the correct link is ranked within the top 20 predictions) metrics. The top three performing models for each dataset and metric are highlighted.

This table compares the performance of various graph neural networks (GNNs) in estimating the number of triangles in a graph. The metric used is the mean squared error (MSE) normalized by the variance of the true triangle counts. Lower values indicate better performance. The results are presented for two types of graphs: Erdos-Renyi and Random Regular graphs.

This table presents the results of link prediction experiments on eight non-attributed benchmark datasets. The performance of various link prediction models is evaluated using Hits@50 as the metric. The table shows the average score and standard deviation for each model on each dataset. The top three performing models are highlighted for each dataset.
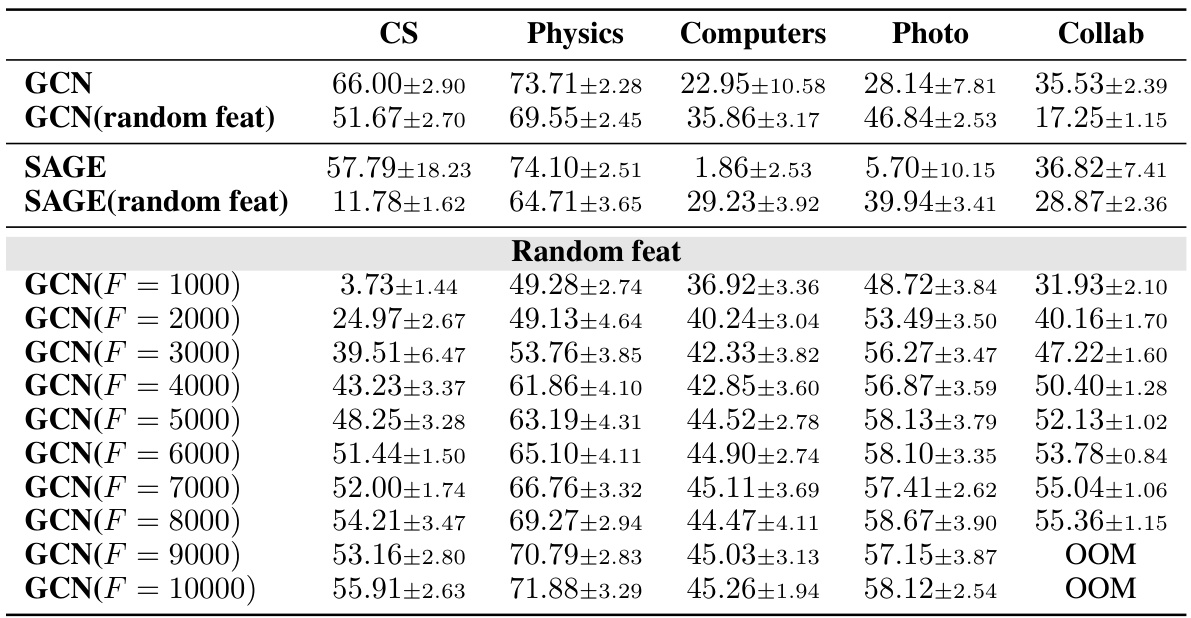
This table presents a comparison of the performance of various Graph Neural Networks (GNNs) on link prediction tasks. It contrasts the use of actual node attributes versus randomly generated vectors as input features for the GNNs. The performance metric used is Hits@50, and all GNNs are configured with two layers for a fair comparison. The results show how different GNNs and feature sets (actual attributes vs. random features) perform on different benchmark datasets.

This table presents the results of link prediction experiments on eight non-attributed benchmark datasets. The performance is measured using Hits@50 (the number of correctly predicted links within the top 50 predictions) and is shown as the average score ± standard deviation across multiple runs. The top three performing models (out of several compared) are highlighted in color-coding.

This ablation study investigates the individual contributions of three key components in the MPLP model: Shortcut removal, One-hot hubs, and Norm rescaling. The results show the performance of MPLP when each of these components is removed, highlighting their impact on the model’s performance for link prediction across multiple attributed benchmark datasets.

This table presents the results of link prediction experiments on eight datasets without node attributes. The performance of several models is compared using the Hits@50 metric (the percentage of correctly predicted links among the top 50 predictions), with the top three models highlighted. The table shows the average score and standard deviation for each model and dataset.

This table presents the results of link prediction experiments on eight non-attributed benchmark datasets. The performance of several link prediction methods, including heuristic baselines (CN, AA, RA), GNN encoders (GCN, SAGE), and state-of-the-art link prediction models (SEAL, ELPH, Neo-GNN, NCNC, MPLP), are compared. The metrics used are Hits@50 for most datasets (except for E.coli which uses Hits@100). The top three performing methods for each dataset are highlighted in color.
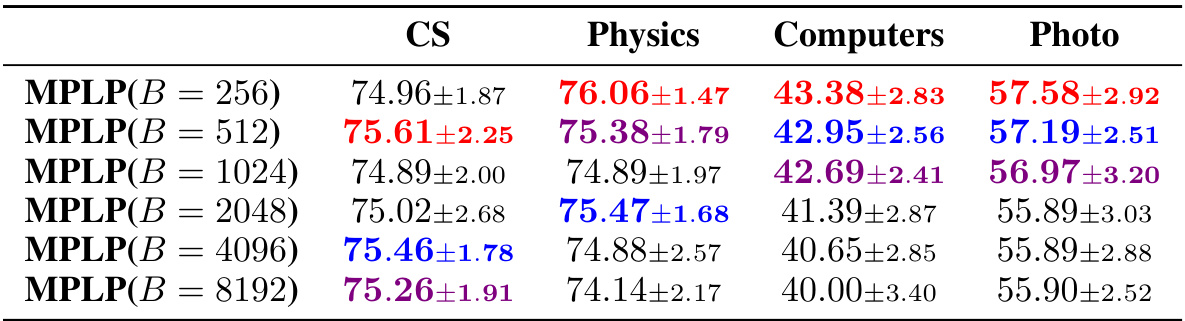
This ablation study investigates the impact of different batch sizes (B) on the performance of the MPLP model for link prediction. The study is conducted on attributed benchmark datasets and evaluates performance using the Hits@50 metric. The table shows the average score and standard deviation for each batch size, with the top three performing models highlighted.

This table presents the results of link prediction experiments on eight non-attributed benchmark datasets. The metrics used are Hits@50 for most datasets, Hits@100 for PPA, and MRR for Citation2. Each result is the average score over ten runs ± standard deviation. The top three performing models for each dataset are highlighted in color.

This table shows the results of an ablation study on the effect of batch size on the performance of the proposed model (MPLP) on attributed benchmark datasets. The study varied the batch size (B) while keeping other hyperparameters constant to determine the impact of this hyperparameter on the link prediction task using Hits@50 as the evaluation metric. The top three performing models for each dataset are highlighted.
Full paper#