↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Multiclass classification often involves optimizing surrogate loss functions, which can be computationally expensive, especially with many classes. Existing approaches typically require high-dimensional embeddings of the classes, hindering efficiency. This paper challenges the need for full consistency by introducing partially consistent surrogates and analyzing their properties under various embedding schemes.
The authors propose a novel method using multiple parallel problem instances to build fully consistent models using these lower-dimensional embeddings. This technique leverages parallelism to avoid known lower bounds on the embedding dimension. The results demonstrate improved computational efficiency without sacrificing prediction accuracy, offering a practical solution to a long-standing challenge in multiclass classification.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers novel methods for handling the computational challenges in multiclass classification, particularly when dealing with a large number of classes. It provides theoretical guarantees for partially consistent surrogate losses and demonstrates how to recover full consistency using multiple, parallelizable problem instances. This is highly relevant to current machine learning trends focusing on high-dimensional data and complex prediction tasks.
Visual Insights#

This figure illustrates the concept of hallucination regions in low-dimensional embeddings for multiclass classification. The left panel shows a 2D embedding of four classes (a, b, c, d) into a unit cube, highlighting the central hallucination region where the model could predict a class that has zero probability under the true distribution. The right panel extends this concept to a 3D embedding of six classes (a, b, c, d, e, f) using a permutahedron, illustrating regions of strict calibration, inconsistency, and hallucinations.
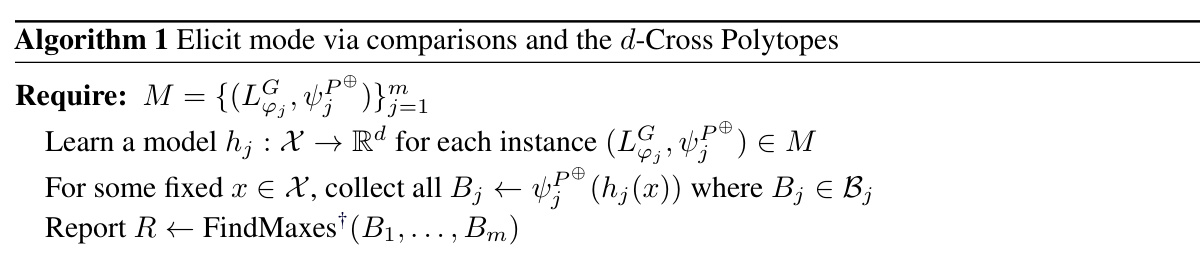
This table lists general mathematical notations used throughout the paper, including symbols for prediction space, label space, probability distributions, loss functions, properties, and other mathematical concepts.
In-depth insights#
Surrogate Loss Tradeoffs#
The concept of ‘Surrogate Loss Tradeoffs’ in multiclass classification centers on the inherent tension between achieving consistent classification and maintaining computational feasibility. Consistency ensures the surrogate loss function accurately reflects the true classification task, leading to optimal predictions. However, designing consistent surrogate losses often requires high dimensionality, increasing computational complexity, especially with many classes. This tradeoff necessitates strategies to balance consistency and dimensionality. Approaches explored include relaxing the strict consistency requirement (partial consistency), utilizing specialized low-dimensional embeddings, and employing parallel computation across multiple problem instances. The analysis of these methods unveils insights into the conditions under which partial consistency guarantees hold, identifying scenarios where reduced dimensionality is acceptable without sacrificing predictive accuracy. The use of multiple problem instances offers a way to recover full consistency despite lower-dimensional surrogates, exploiting parallelization to mitigate increased computational cost. Ultimately, the optimal strategy depends on the specific problem characteristics, such as the number of classes and the computational resources available. Future work may focus on refining partial consistency bounds, developing more efficient low-dimensional embeddings, or exploring new methods for aggregating results across multiple parallel computations to improve efficiency and maintain high accuracy.
Polytope Embeddings#
Polytope embeddings offer a novel approach to multiclass classification by representing discrete outcomes as vertices of a polytope in a lower-dimensional space. This method cleverly trades off consistency—the guarantee that minimizing the surrogate loss leads to correct classifications—for computational tractability. The core idea is to embed n outcomes into d dimensions, where d<n, which is crucial for handling high-dimensional problems. While this embedding inherently introduces inconsistencies (hallucinations), the paper rigorously analyzes the extent of these inconsistencies under low-noise assumptions, identifying regions where calibration is maintained. This involves defining strict calibrated regions, subsets of the probability simplex where the surrogate loss is calibrated for the 0-1 loss, even with dimensionality reduction. The trade-off is carefully examined, showcasing that even with partial consistency, reasonable performance can be achieved with significant computational savings. The introduction of polytope embeddings also enables the construction of consistent surrogate losses through the use of multiple problem instances, enabling a parallelizable approach to sidestep limitations on d, thereby enhancing both efficiency and scalability.
Hallucination Analysis#
A hallucination analysis in the context of a machine learning model, specifically focusing on multiclass classification, would dissect the instances where the model outputs a prediction that is not supported by the underlying data distribution. This would involve examining the model’s decision boundaries and the factors that lead to such misclassifications. The analysis might identify specific regions in the input space where hallucinations are more prevalent, indicating potential weaknesses in the model’s training or architecture. Investigating the frequency and distribution of hallucinations across different classes or data subsets is key to gaining actionable insights. It could reveal biases in the model or data imbalances. By quantifying the severity of hallucinations (e.g., using a metric that measures the discrepancy between predicted probability and true probability), a more comprehensive understanding of the model’s reliability and areas for improvement can be obtained. Ultimately, the goal of a hallucination analysis is to guide improvements in model design, data preprocessing, or training techniques to reduce or mitigate the occurrence of these errors. The analysis might lead to better regularization strategies, improved feature engineering, or the development of more robust loss functions.
Low Noise Consistency#
The concept of ‘Low Noise Consistency’ in a classification setting centers on the reliability of a surrogate model’s predictions under conditions where the true data distribution is not excessively noisy. The core idea is to find a balance between computational tractability (achieved by using lower dimensional surrogates) and the theoretical guarantees of consistency (perfect correspondence between surrogate and true risk minimization). In a noisy environment, a low-dimensional surrogate might not perfectly capture the intricacies of the true classification problem, potentially leading to suboptimal predictions. However, under a ’low-noise’ assumption—meaning the true labels are predominantly clear and not heavily obscured by random fluctuations—the surrogate model’s simplified representation is more likely to yield accurate and consistent results. This approach is particularly valuable in high-dimensional problems, where fully consistent high-dimensional surrogates may be computationally prohibitive. The analysis of low-noise consistency involves studying calibration properties under the imposed noise constraints, examining the trade-offs between consistency, dimensionality, and the noise level, and ultimately, determining conditions under which the surrogate’s predictions align with the true classification task in a reliable manner. Investigating different embedding techniques into low dimensional spaces and analyzing their resulting behavior under varying noise conditions are essential aspects of this analysis. The practical implications focus on designing surrogates that are more computationally efficient while maintaining adequate performance under realistic, slightly noisy conditions frequently observed in real-world data.
Multi-Instance Elicitation#
Multi-instance elicitation presents a novel approach to overcome limitations in traditional elicitation methods, particularly concerning high dimensionality. By strategically employing multiple lower-dimensional surrogate loss functions and cleverly aggregating their predictions, it aims to sidestep computational challenges associated with high-dimensional problems. The framework hinges on the concept of partial consistency, acknowledging that perfect consistency may not be achievable with reduced dimensionality. This tradeoff between consistency and dimensionality is a core aspect of the approach, emphasizing its practicality. The method’s success depends on the selection of suitable embeddings and the development of effective aggregation techniques to ensure reliable inference of properties from the ensemble of partial responses. A key strength is the potential for parallelization, making the approach scalable for large-scale applications. The theoretical underpinnings emphasize the importance of carefully chosen polytope embeddings and the use of low-noise assumptions to achieve robust calibration. However, future research should investigate the optimal number of instances required and explore strategies for effective instance selection to optimize efficiency.
More visual insights#
More on figures

The figure shows two examples of polytope embeddings of probability distributions over outcomes. The left panel shows a 2D embedding of four outcomes into a unit square; the central region represents the hallucination region, where reports minimize surrogate loss even though the true distribution has zero weight on the prediction. The right panel shows a 3D embedding of six outcomes into a permutahedron, color-coded to illustrate different regions of consistency and inconsistency.

This figure shows two examples of polytope embeddings for multiclass classification. The left panel shows a 2D embedding of four outcomes into a unit cube, highlighting the hallucination region at the origin. The right panel shows a 3D embedding of six outcomes into a permutahedron, illustrating strict calibration regions, inconsistency regions, and hallucination regions.
More on tables

This table lists the notations used throughout the paper. It includes mathematical symbols representing prediction spaces, label spaces, probability distributions, index sets, convex sets, surrogate prediction spaces, projections, permutations, losses (discrete and surrogate), link functions, expected losses, properties, level sets of properties, and the zero-one loss and mode property.

This table lists notations related to polytopes and their embeddings, including the definitions of a polytope, its vertices, edges, and embeddings in various spaces (unit cube, permutahedron, cross polytope). It also includes notations for Bregman divergence, induced loss function, and the Maximum A Posteriori (MAP) link.

This table presents notations related to calibration regions. It includes notations for hallucination regions, strict calibrated regions, intersections and unions of link level sets and strict calibrated regions, low noise assumptions, scaled vertex sets, and scaled versions of polytopes anchored at vertices.
Full paper#



















