Simplified and Generalized Masked Diffusion for Discrete Data

↗ OpenReview ↗ NeurIPS Homepage ↗ Hugging Face ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers in generative modeling because it simplifies and generalizes masked diffusion models for discrete data, a challenging area with limited success compared to continuous models. The simplified framework and ELBO objective improve training stability and performance, while the generalization to state-dependent masking schedules opens new avenues for innovation. This work’s impact extends to various applications involving discrete data, such as text and image generation.

Visual Insights

#

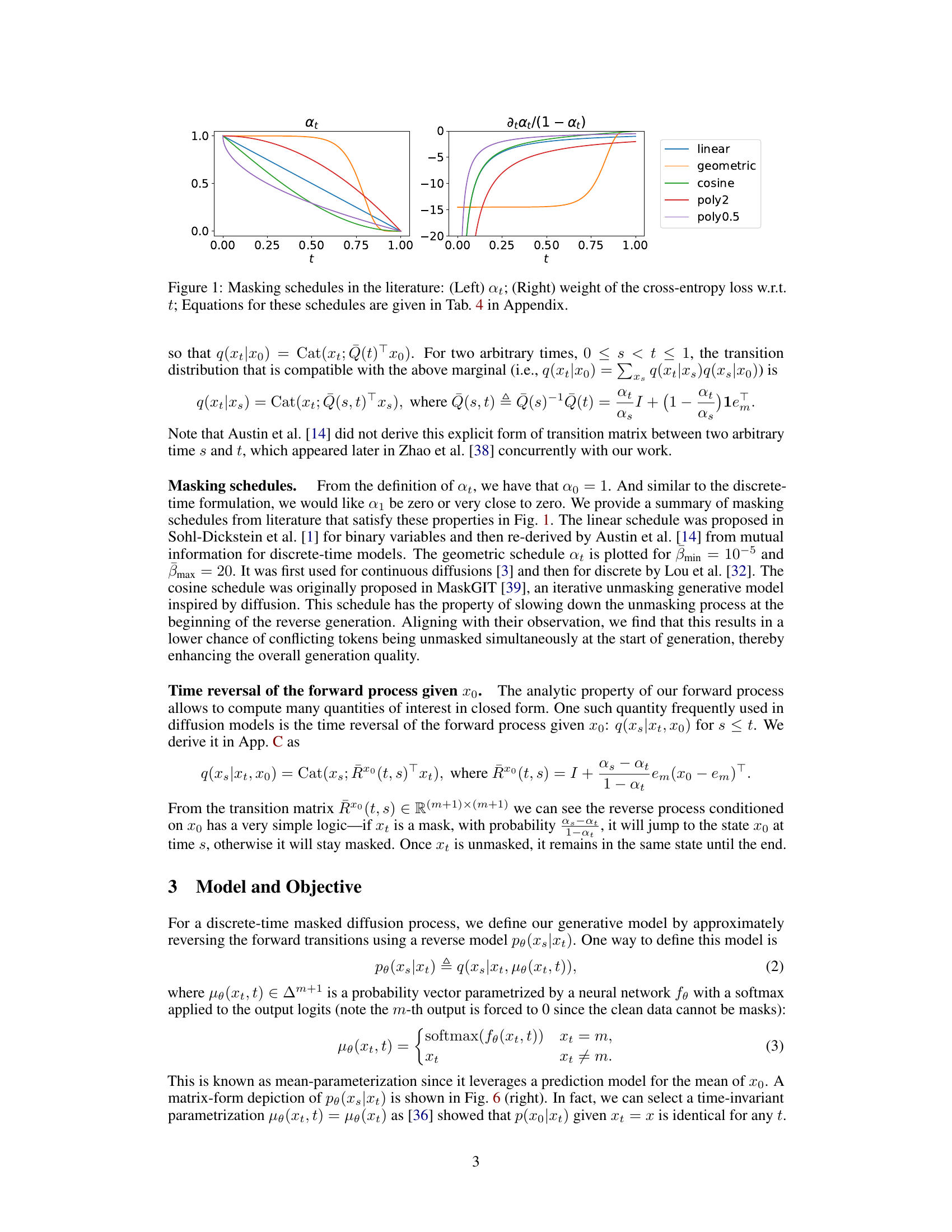
This figure shows different masking schedules used in the literature for masked diffusion models. The left panel displays the function a_t, which represents the probability of a token remaining unmasked at time t. The right panel shows the weight of the cross-entropy loss with respect to time t. Various schedules are presented, including linear, geometric, cosine, and polynomial functions, each having different properties and potentially influencing the training and sampling process.

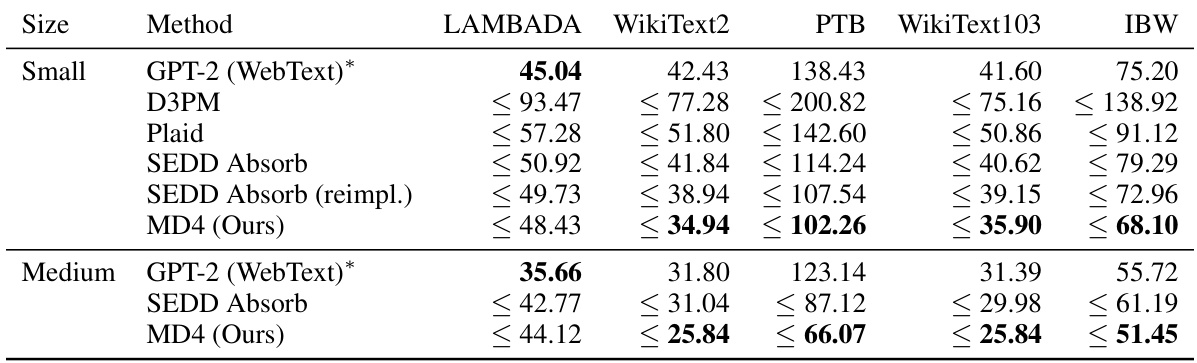
This table presents the zero-shot unconditional perplexity results on five benchmark datasets (LAMBADA, WikiText2, PTB, WikiText103, and IBW) for several methods, including GPT-2, D3PM, Plaid, SEDD Absorb, and the authors’ proposed MD4 model. The results are broken down by model size (small and medium). The table highlights that MD4 achieves superior performance compared to other methods on most datasets, showcasing its effectiveness in zero-shot text generation.

In-depth insights

#

Masked Diffusion

#

Masked diffusion, a generative modeling approach, offers a compelling alternative to autoregressive models, particularly for discrete data. Its core idea involves a forward process that gradually masks or absorbs the data, followed by a reverse process that reconstructs it. This framework presents several advantages: it avoids the sequential constraints of autoregressive models, enabling parallel processing and potentially faster generation. Furthermore, it offers a more flexible approach to modeling discrete data: unlike continuous diffusion, which requires embedding discrete data into a continuous space, masked diffusion directly handles discrete states. However, previous works suffered from complex formulations and unclear relationships between different perspectives, leading to suboptimal results. This paper addresses these limitations by providing a simplified and generalized framework. By showing the continuous-time variational objective is simply a weighted integral of cross-entropy losses, the paper significantly clarifies the underlying theory and enables the development of more efficient models. The use of state-dependent masking schedules further enhances the model’s flexibility and performance. The demonstrated superior results on text and image modeling tasks highlight the effectiveness of this refined approach and pave the way for future improvements in generative modeling.

ELBO Objective

#

The ELBO (Evidence Lower Bound) objective is central to training masked diffusion models. The paper’s key contribution lies in simplifying the ELBO expression, showing it’s a weighted integral of cross-entropy losses over time. This elegant formulation contrasts with previous, more complex approaches, offering improved training stability and efficiency. The simplified ELBO also reveals invariance properties related to the signal-to-noise ratio, similar to continuous diffusion models, which is insightful from a theoretical perspective. The simplified objective enables the training of generalized models with state-dependent masking schedules, offering further performance gains. This simplification and unification are crucial for broader adoption and improved understanding of masked diffusion models, and it highlights the power of a continuous-time perspective in simplifying the training objective for discrete diffusion processes.

State-dependent Masking

#

The concept of ‘state-dependent masking’ in the context of masked diffusion models introduces a significant advancement. Instead of a global masking schedule, where the probability of masking a token is solely determined by time, state-dependent masking allows this probability to depend on the token’s value and its context within the sequence. This flexibility offers the potential for improved performance, particularly in applications where some tokens are inherently more important than others, for example, in text generation, where certain words may carry greater semantic weight than others. The key advantage is that it enables more nuanced control over the generation process, potentially leading to higher-quality samples with improved coherence and less noise. This approach likely leads to a more efficient learning process, as the model can prioritize revealing crucial tokens, reducing conflicts during the unmasking process. While the implementation and training of state-dependent masking methods may pose complexities—such as the need for careful parameterization and efficient gradient estimation—the potential gains in terms of model performance and sample quality make it a promising area of future research.

Discrete Diffusion

#

Discrete diffusion models offer a compelling approach to generative modeling of discrete data, addressing limitations of continuous diffusion models in handling categorical variables. The core challenge lies in defining an appropriate forward diffusion process that maps discrete data to a masked state, while also ensuring reversibility for generation. This often involves intricate transition matrices and careful selection of masking schedules. The paper highlights a simplified and generalized framework that clarifies the relationships between different perspectives (continuous-time vs. discrete-time), leading to improved parameterizations and objectives. A crucial contribution is the derivation of a simple ELBO expression, revealing the objective as a weighted integral of cross-entropy losses, facilitating efficient training. The generalized model introduces state-dependent masking, further enhancing performance by allowing flexibility in how masking is applied to different data points. The results demonstrate significant improvements over prior discrete diffusion approaches, achieving competitive performance on both text and image modeling tasks. The key takeaway is the framework’s simplification and generalization, which remove prior complexities and open the way for more efficient and effective discrete diffusion models.

Future Work

#

Future research directions stemming from this work on simplified and generalized masked diffusion for discrete data could focus on several key areas. Improving the efficiency and scalability of state-dependent masking schedules is crucial, as the current approach can be computationally expensive and prone to overfitting. Further investigation into the underlying theoretical properties of state-dependent masking and its effect on model performance is needed. Exploring alternative architectures for discrete diffusion models, potentially inspired by recent advances in autoregressive models, could yield significant improvements in sample quality and computational efficiency. Extending the models to handle more complex data modalities, such as time series, graphs, and multimodal data, presents a significant challenge but offers considerable potential. Finally, developing more robust evaluation metrics for discrete generative models that better capture the nuances of generated samples is necessary to fairly compare different approaches. Addressing these future research directions will lead to more powerful and versatile discrete diffusion models with broad applications.

More visual insights

#

More on figures

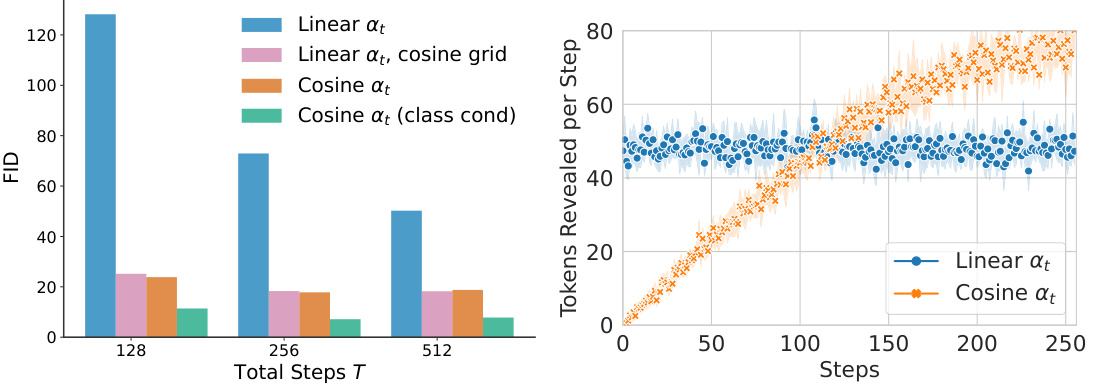
This figure presents two sub-figures. The left sub-figure is a bar chart that shows the Fréchet Inception Distance (FID) score for 50,000 image samples generated by the model on the ImageNet 64x64 dataset. The FID score is a metric for evaluating the quality of generated images, with lower scores indicating better image quality. Different sampling configurations are compared, including linear and cosine masking schedules with and without class conditioning. The right sub-figure is a line chart that shows the number of tokens revealed at each generation step for linear and cosine masking schedules. This illustrates how the unmasking process unfolds over time for the different schedules.

This figure shows an example of the iterative unmasking process during text generation using the MD4 model. The process starts with a sequence of masked tokens (represented by ‘?’). The model then progressively unmasks these tokens in steps, revealing them sequentially in the colors green, yellow, and red, until a complete sentence is generated. The figure highlights how the model gradually reconstructs the text from a masked state, showcasing the iterative nature of the generation process.

This figure shows the perplexity on the OpenWebText validation set during the training process for several models: Gaussian Diffusion-S, SEDD-S, MD4-S, GenMD4-S, and MD4-M. The x-axis represents the training steps (in units of 1000 steps), and the y-axis represents the perplexity. The plot illustrates the training progress of different models and their final perplexities on this dataset. The final perplexity values are also detailed in Table 5 of the Appendix.

This figure shows several unconditional image samples generated by the MD4 model trained on the ImageNet 64x64 dataset. The images demonstrate the model’s ability to generate diverse and visually coherent images at 64x64 resolution by treating each pixel as a discrete token.

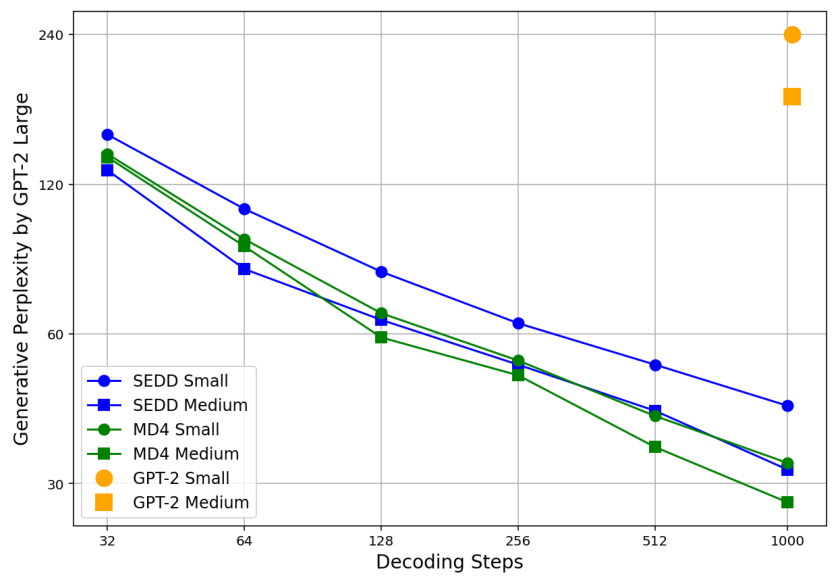
This figure compares the performance of MD4 and SEDD, two discrete diffusion models, against GPT-2, an autoregressive model, in generating 1024-token text sequences. The comparison is made using the generative perplexity metric, as evaluated by GPT-2 Large. The plot shows how perplexity changes with different decoding steps and model sizes (small vs. medium). This helps understand the impact of model size and decoding length on sample quality.

This figure displays several more unconditional samples generated by the MD4 model trained on the ImageNet 64x64 dataset. These samples demonstrate the model’s ability to generate a variety of images from the dataset without any specific conditional input. The quality of the samples varies, reflecting the challenges inherent in generating high-quality images from discrete data. The model is trained to maximize likelihood rather than visual quality.

This figure shows a comparison of different masking schedules used in the literature for masked diffusion models. The left panel displays the function at over time, where at represents the probability that a data point remains unmasked at time t. The right panel shows the corresponding weight of the cross-entropy loss with respect to time t in the ELBO (Evidence Lower Bound) objective function. Several different schedules are plotted, including linear, geometric, cosine and polynomial functions, highlighting their distinct behaviors in controlling the unmasking process over time.

More on tables

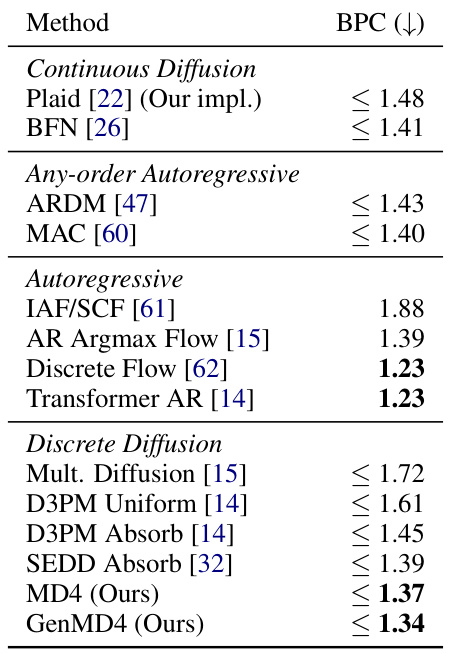
This table presents the Bits Per Character (BPC) results for various models on the Text8 test dataset. The models are categorized into Continuous Diffusion, Any-order Autoregressive, Autoregressive, and Discrete Diffusion. The table compares different approaches to text modeling in terms of their performance in terms of bits per character. Lower BPC indicates better performance.

This table compares the performance of various autoregressive and diffusion models on image generation tasks. The metrics used is bits per dimension (BPD), a measure of how well the model compresses the image data. Lower BPD values indicate better performance. The table is divided into autoregressive and discrete diffusion models, and further subdivided into CIFAR-10 and ImageNet 64x64 datasets, showcasing the model performance at different scales and complexities.

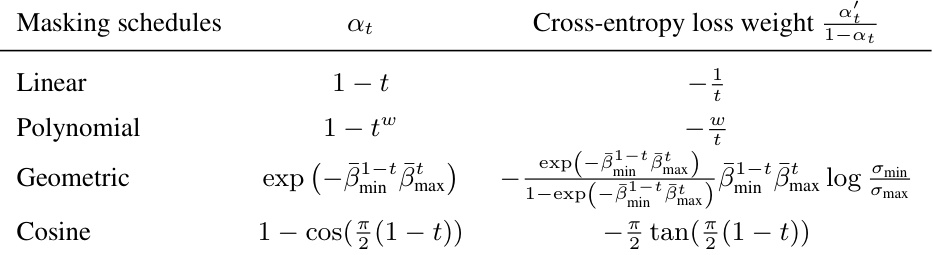
This table presents the zero-shot unconditional perplexity results on five benchmark datasets (LAMBADA, WikiText2, PTB, WikiText103, and IBW) for several language models. The models compared include GPT-2, D3PM, Plaid, SEDD Absorb (both the original and a re-implementation), and the authors’ MD4 model. The table highlights the superior performance of the MD4 model, achieving the best perplexity scores on four out of five datasets and second-best on the remaining one. The table also notes a difference in the GPT-2 results due to the use of different training datasets.

This table presents the perplexity scores achieved on the OpenWebText validation set for different models. The perplexity metric measures how well a language model predicts a sequence of words. Lower perplexity indicates better performance. The table shows the results for different model sizes (small and medium) and methods, including Gaussian diffusion models, SEDD Absorb (reimplementation), MD4 (the proposed model), and GenMD4 (a generalized version of MD4).

This table presents an ablation study on the impact of discretization on the zero-shot perplexity of the MD4 model. It compares the perplexity scores obtained using different numbers of timesteps (T) for the model’s reverse diffusion process on various text datasets. The continuous-time limit (T = ∞) is also included as a reference point. This helps to understand how the discretization level in the sampling process affects the model’s performance.

Full paper

#