↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many real-world problems involve finding the optimal solution among many possibilities, a field called combinatorial optimization. Current methods like diffusion models are powerful but slow. The core issue is the time-consuming iterative sampling process required for generating high-quality solutions.
This paper introduces Fast T2T, which employs an ‘optimization consistency’ training protocol. This clever method teaches the model to directly map noisy data to optimal solutions. Fast T2T achieves significantly faster solution generation while maintaining solution quality. Extensive experiments on well-known problems (Traveling Salesman Problem, Maximal Independent Set) demonstrate Fast T2T’s superior performance over existing techniques, achieving speedups of tens or even hundreds of times.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in combinatorial optimization and machine learning. It introduces a novel and efficient approach for solving complex optimization problems, surpassing state-of-the-art methods in both speed and accuracy. This opens new avenues for applying diffusion models to various optimization tasks and inspires further research on consistency-based training methods. Its focus on bridging the gap between training and testing is also highly relevant to the broader field of machine learning.
Visual Insights#
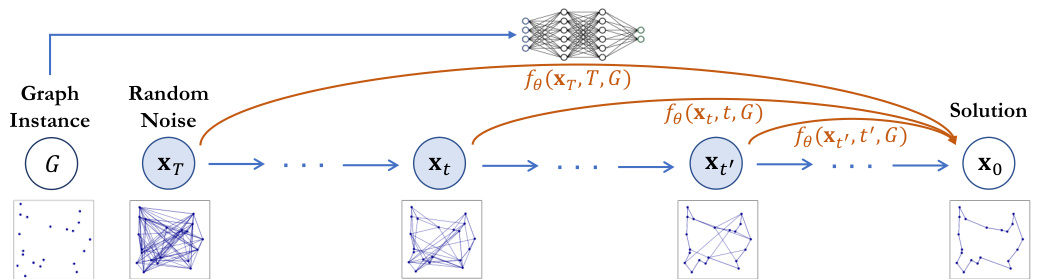
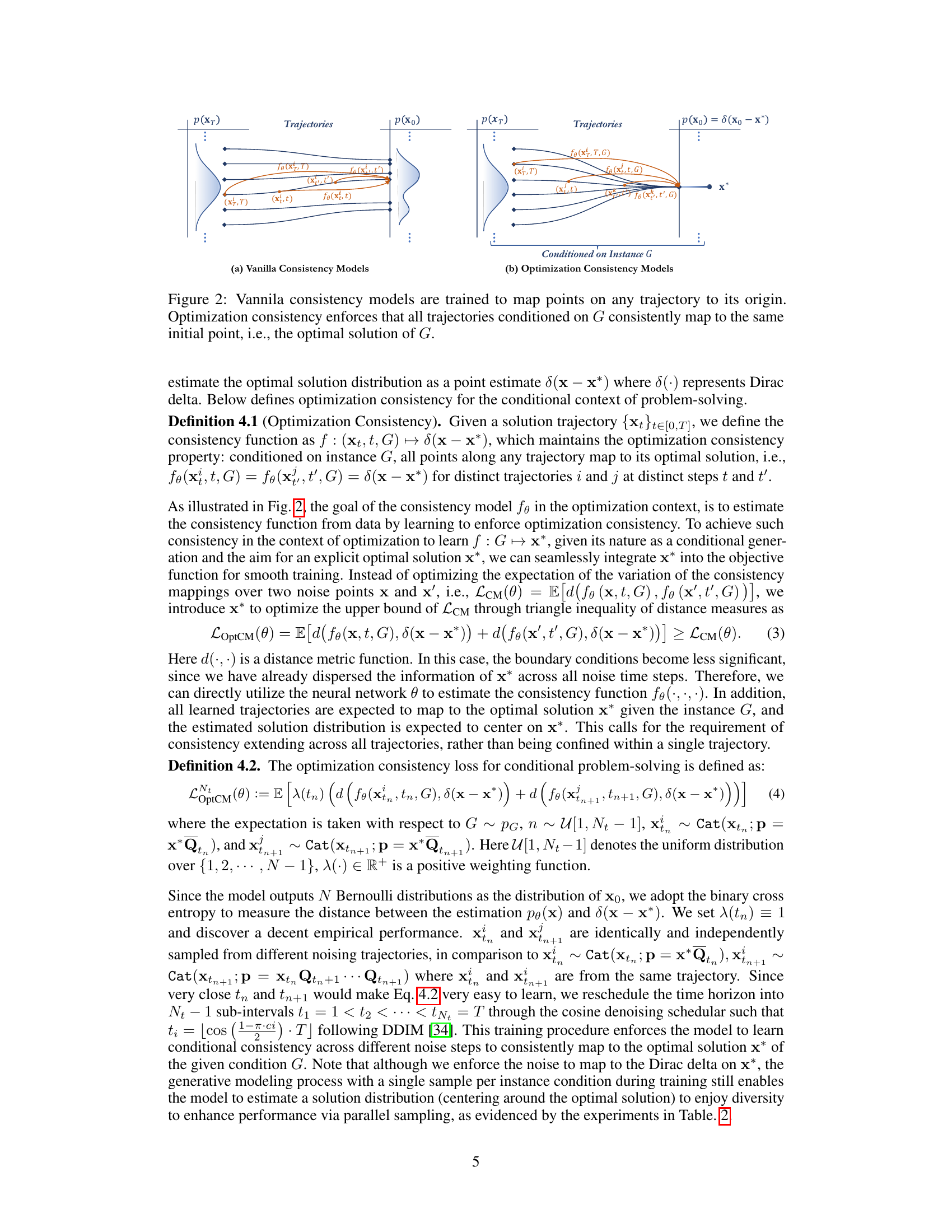
This figure illustrates the optimization consistency model for combinatorial optimization (CO) problems. It shows how the model learns to map from different noise levels (represented by the xT, Xt, Xt’ variables) to the solution distribution (x0), given a problem instance (G). The model learns a function fθ that connects these noise levels to the solution. The model is trained to minimize the difference among samples originating from varying generative trajectories and time steps relative to the optimal solution. This allows for high-quality solution generation with minimal steps, improving efficiency.

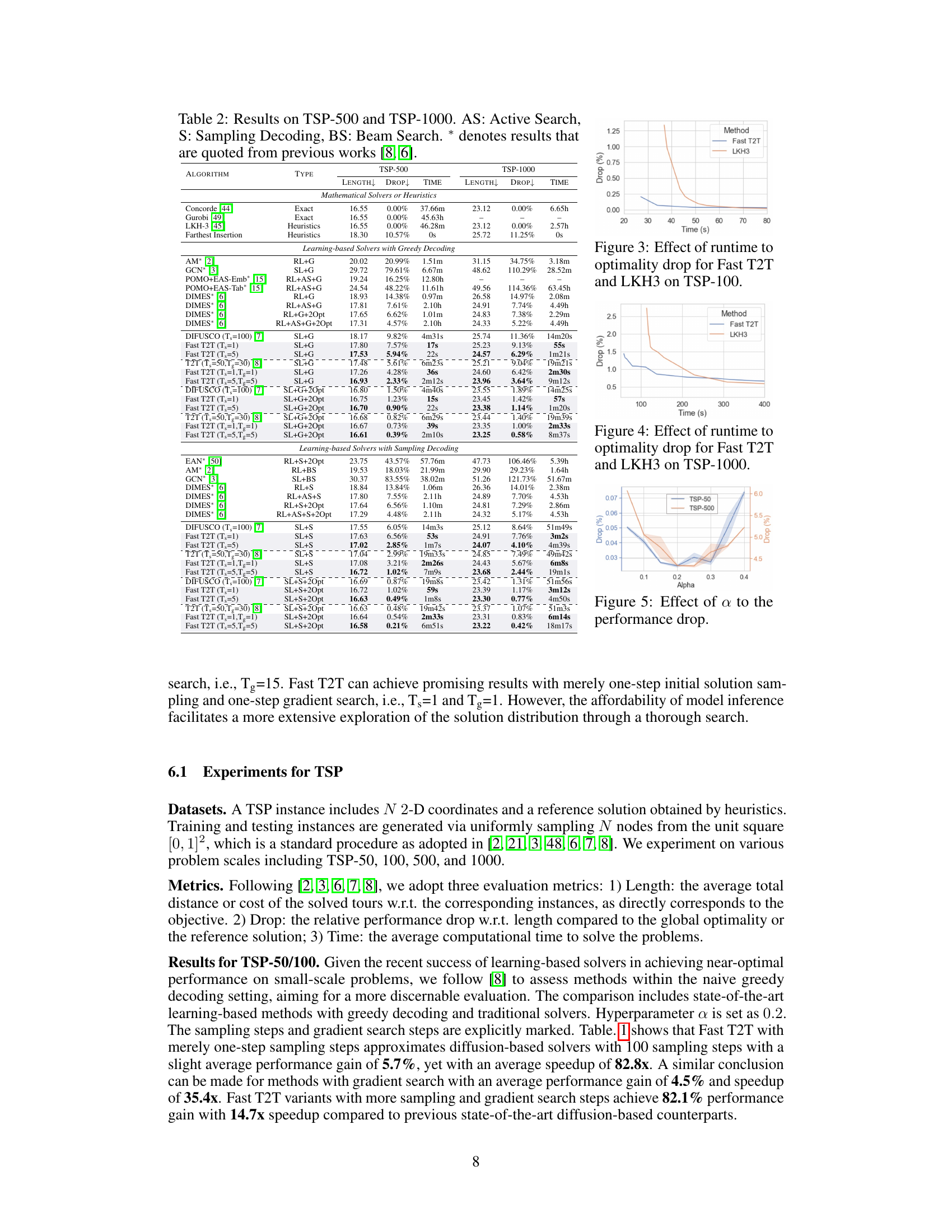
This table compares the performance of various algorithms on the Traveling Salesman Problem (TSP) with 50 and 100 cities. The algorithms are categorized into exact solvers (providing optimal solutions), heuristics (approximations), and learning-based solvers using greedy decoding. The metrics used are solution length (how long the tour is), the percentage drop in length compared to the optimal solution, and the computation time required. The learning-based methods are further distinguished by whether they use reinforcement learning (RL) or supervised learning (SL). Asterisks (*) indicate that the results were taken from prior published works. The table highlights the performance of Fast T2T in comparison to these other methods.
In-depth insights#
Optimization Consistency#
The core concept of “Optimization Consistency” revolves around enforcing agreement among solution trajectories generated from varying noise levels in diffusion models for combinatorial optimization. Instead of relying on iterative denoising, the model learns direct mappings from different noise levels to the optimal solution. This approach significantly accelerates the solution generation process, achieving comparable quality with substantially fewer steps. Consistency training minimizes differences between samples from diverse trajectories, improving solution robustness. By directly targeting the optimal solution, the method bypasses the computationally expensive iterative refinement inherent in traditional diffusion models. The single-step solution generation is further enhanced by a consistency-based gradient search that effectively explores the learned solution space during testing, leading to improved solution quality and efficiency.
Fast T2T Framework#
The Fast T2T framework presents a novel approach to combinatorial optimization by leveraging the strengths of diffusion models while mitigating their computational cost. Optimization consistency is key; the model directly learns mappings from noise levels to optimal solutions, enabling fast, single-step generation. This contrasts with traditional diffusion methods’ iterative sampling. The framework further incorporates a consistency-based gradient search during testing, allowing for refined exploration of the learned solution space. Bridging the training-to-testing gap, this gradient search effectively guides the model towards optimal solutions for unseen instances. Empirical results across TSP and MIS problems showcase Fast T2T’s superiority in both solution quality and efficiency, significantly outperforming state-of-the-art diffusion-based methods with a substantial speedup.
Gradient Search#
The paper introduces a novel gradient search method within a training-to-testing framework for combinatorial optimization. Instead of relying solely on the diffusion model’s iterative sampling, the gradient search refines the solution by leveraging the learned optimization consistency mappings. This approach updates the latent solution probabilities, guided by the objective function’s gradient, during the denoising process. It bridges the gap between training and testing, allowing the model to effectively explore the solution space learned during training when encountering unseen instances. The gradient search operates on the learned consistency mappings, directly incorporating objective feedback, which contrasts with the iterative denoising approach of traditional diffusion models. This is particularly advantageous for efficiency as it drastically reduces computation time by avoiding multiple denoising steps. The effectiveness of this consistency-based gradient search is empirically validated through experiments, demonstrating the method’s improved performance in solution quality and speed, even exceeding state-of-the-art approaches. The one-step gradient search is notably faster, achieving significant speedups compared to diffusion-based alternatives requiring many steps.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims and demonstrating the effectiveness of the proposed method. A strong empirical results section should present a comprehensive evaluation across various metrics, datasets and baselines. Rigorous experimental design, including appropriate controls and statistical testing, is essential for ensuring the reliability of the findings. Clear presentation of results with relevant figures and tables, along with a detailed discussion interpreting the results in the context of prior work, is paramount. The results should show the superiority of the proposed method compared to existing state-of-the-art techniques. A detailed analysis of both the strengths and limitations of the proposed methods should also be included. Addressing potential confounding factors and providing insightful explanations for any unexpected outcomes strengthens the analysis. Finally, a discussion on the generalizability and scalability of the approach further enhances the overall impact of the empirical evaluation.
Future Work#
Future research directions stemming from this work could explore extending the optimization consistency framework to other combinatorial optimization problems, beyond TSP and MIS, such as the Quadratic Assignment Problem or Graph Coloring. Investigating alternative architectures for the consistency function, perhaps leveraging more advanced neural network designs or incorporating inductive biases from the problem structure, could further enhance efficiency and solution quality. A key area for improvement is bridging the gap between training and testing data distributions to improve robustness. This could involve more sophisticated data augmentation or domain adaptation techniques. Finally, exploring the integration of optimization consistency with other solution methods, such as local search heuristics or metaheuristics, could create hybrid solvers capable of achieving superior performance and scalability.
More visual insights#
More on figures
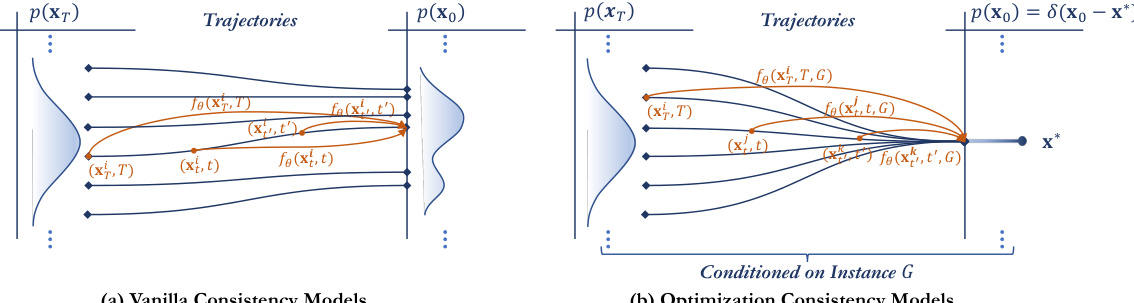
The figure illustrates the difference between vanilla consistency models and optimization consistency models. Vanilla consistency models map points on any trajectory to its origin, while optimization consistency models ensure that all trajectories, conditioned on the problem instance G, consistently map to the same optimal solution. This is achieved by minimizing the difference between the model’s predictions for different noise levels and the optimal solution. The optimization consistency condition ensures that the model generates consistent solutions even from varying noise levels and trajectories, thus improving solution quality and efficiency.
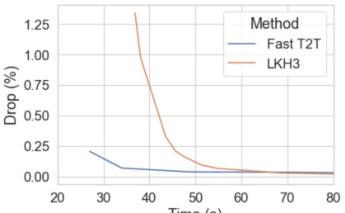
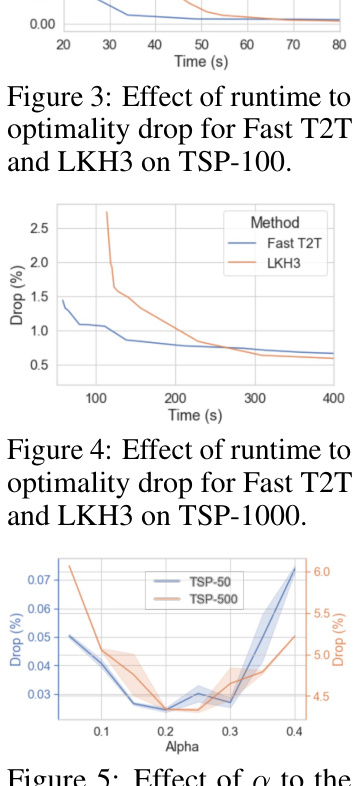
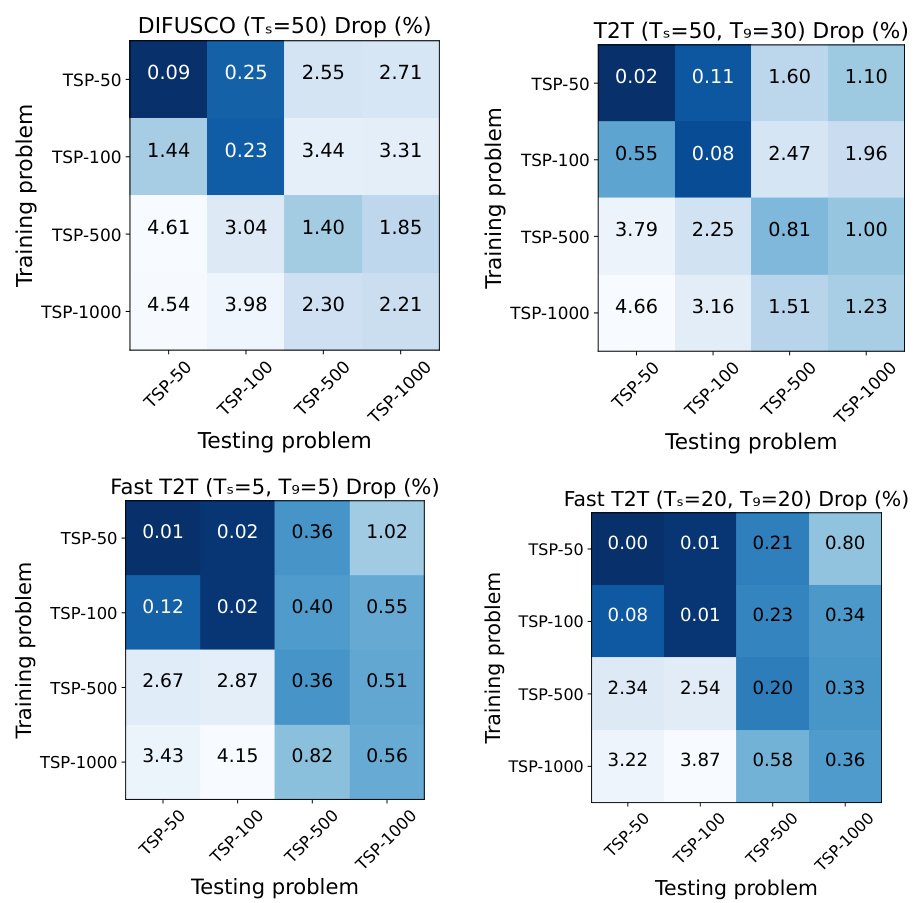
This figure shows the relationship between runtime and solution quality (optimality drop) for two algorithms: Fast T2T and LKH3, on the TSP-100 problem. It demonstrates how the optimality drop decreases as runtime increases for both algorithms but highlights Fast T2T’s faster convergence towards a near-optimal solution.
This figure compares two types of consistency models for combinatorial optimization. The vanilla consistency model trains the model to map any point on a trajectory to its origin. The optimization consistency model adds a constraint: conditioned on a given problem instance, all points along any trajectory must map to the optimal solution. This constraint ensures that the model focuses on finding the optimal solution and improves the efficiency and effectiveness of the model.
This figure compares two types of consistency models: Vanilla consistency models and Optimization consistency models. The Vanilla models simply map points from any trajectory to their origin. In contrast, the Optimization consistency models ensure that all trajectories conditioned on a given graph instance G converge to the same initial point, which represents the optimal solution for that instance. This optimization consistency property is crucial for efficiently solving combinatorial optimization problems.
More on tables
This table compares the performance of various algorithms, including the proposed Fast T2T, on two Traveling Salesman Problem (TSP) instances, TSP-50 and TSP-100. The algorithms are categorized by type (exact, heuristic, reinforcement learning with greedy decoding, or supervised learning with greedy decoding), and their performance is measured by tour length, percentage drop from the optimal solution, and runtime. The table highlights the superior performance of Fast T2T in terms of both solution quality and efficiency.
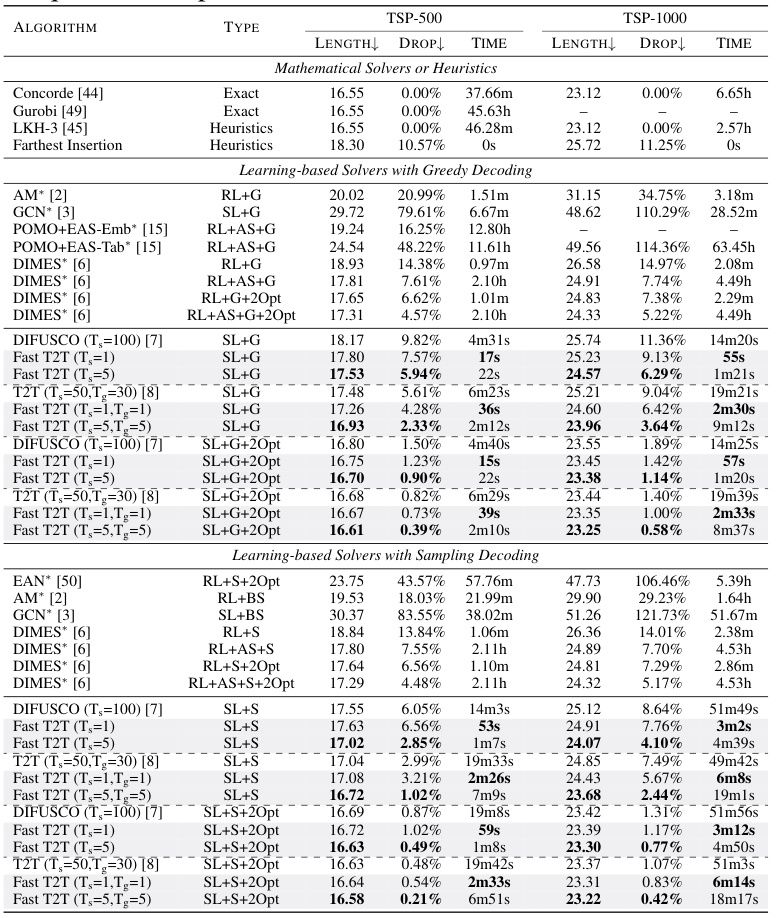
This table compares the performance of Fast T2T against other state-of-the-art methods for solving the Traveling Salesman Problem (TSP) with 50 and 100 cities. The metrics used are solution length, the percentage drop in length compared to the optimal solution, and the time taken to find the solution. The table includes results from exact solvers, heuristics, and various learning-based approaches using greedy decoding. It highlights the speed and accuracy advantages of Fast T2T, even when using a single step for both solution generation and gradient search.
This table compares the performance of various algorithms, including the proposed Fast T2T model, on two instances of the Traveling Salesman Problem (TSP): TSP-50 (50 cities) and TSP-100 (100 cities). The metrics used are solution length (how long the tour is), the percentage drop in length compared to the optimal solution (indicating the quality of the approximation), and the time taken to find the solution. Different algorithm types are included (reinforcement learning, supervised learning, and heuristic methods). The table helps showcase the speed and solution quality advantages of Fast T2T, particularly when compared to previous state-of-the-art diffusion-based methods.
This table compares the performance of Fast T2T with several other algorithms (including exact and heuristic methods) on two instances of the Traveling Salesman Problem (TSP), one with 50 cities and one with 100 cities. The comparison considers solution length, the percentage difference from the optimal solution length (drop), and the time taken to find a solution. The table highlights Fast T2T’s superior performance and efficiency, particularly when using only one step for generating solutions and one step for gradient search.

This table compares the performance of Fast T2T with other state-of-the-art methods on two instances of the Traveling Salesman Problem (TSP), one with 50 cities and the other with 100 cities. The metrics used are solution length, percentage drop in length compared to optimal, and inference time. Different algorithms are categorized by their type (exact, heuristic, reinforcement learning, and supervised learning) and whether they use greedy decoding or not. The table highlights Fast T2T’s superiority in terms of both solution quality and efficiency.

This table compares the performance of Fast T2T against other state-of-the-art methods for solving the Traveling Salesman Problem (TSP) with 50 and 100 cities. Metrics include solution length, the percentage difference from the optimal solution (drop), and the time taken to find the solution. The table shows Fast T2T’s competitive performance, especially when considering its speed. Different approaches are categorized as using Reinforcement Learning (RL) or Supervised Learning (SL) and whether they used greedy decoding.
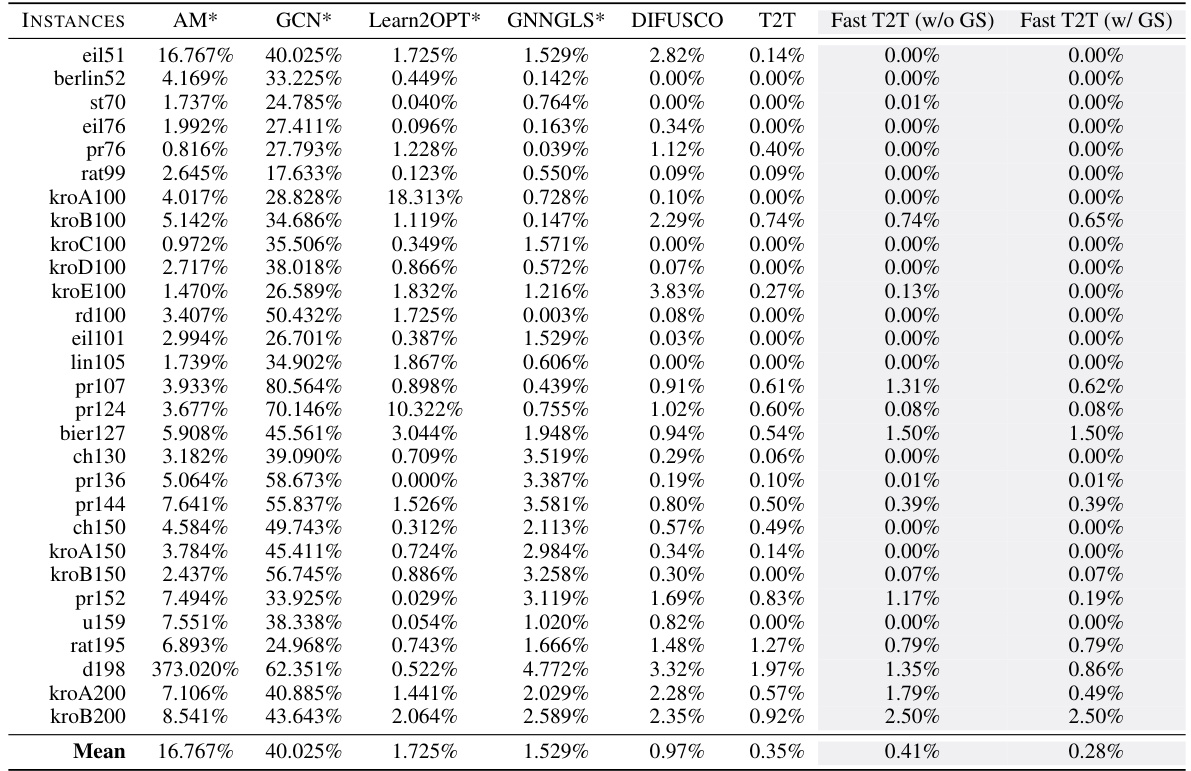
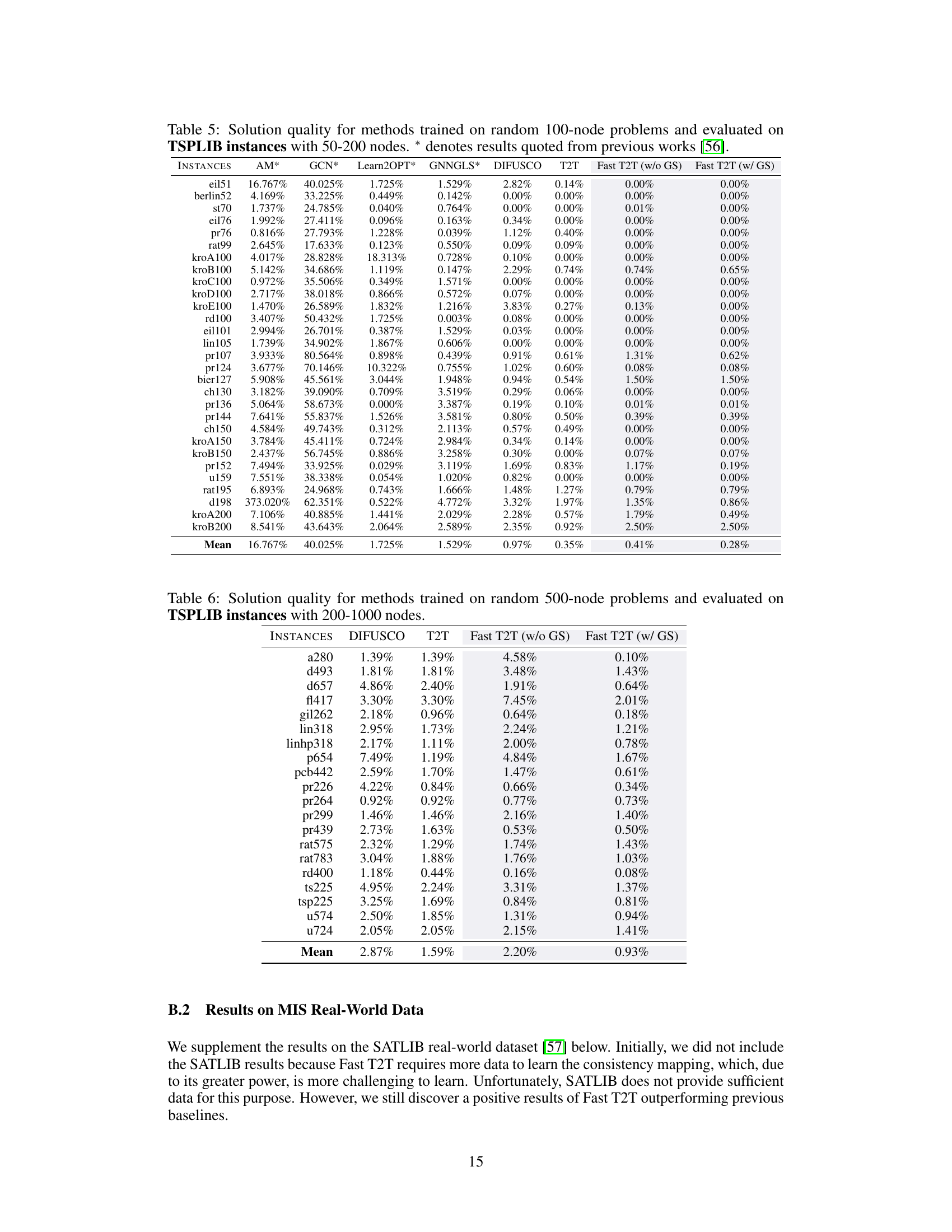
This table compares the performance of various methods (AM, GCN, Learn2OPT, GNNGLS, DIFUSCO, T2T, and Fast T2T with and without gradient search) on TSPLIB instances with 50-200 nodes. The methods were trained on random 100-node problems. The results are presented in terms of solution quality, measured as the percentage drop in tour length relative to the optimal solution. The table shows that Fast T2T consistently achieves superior performance.
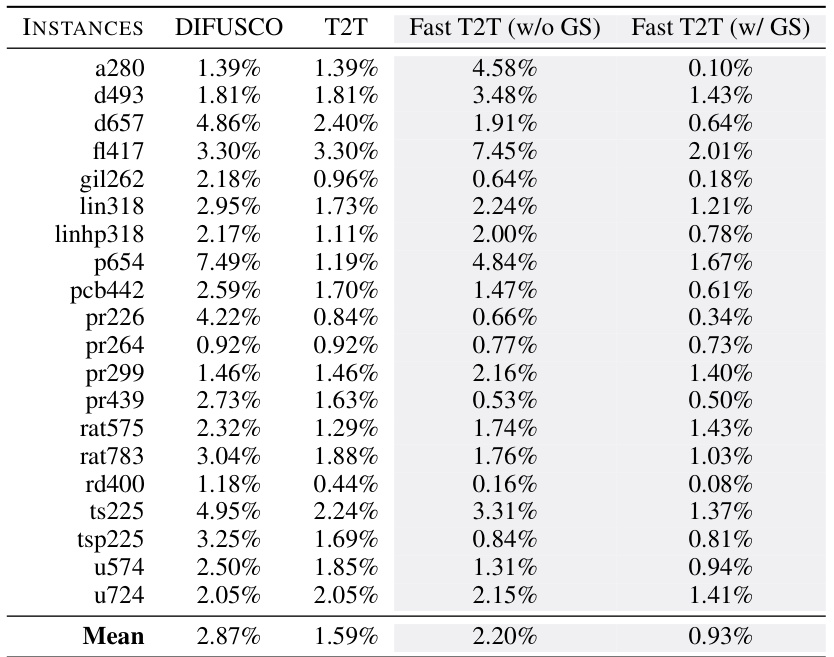
This table presents the performance of different methods on larger TSPLIB instances (200-1000 nodes). The methods were initially trained on randomly generated 500-node TSP problems. The table shows the average optimality gap (Drop) for each method across various test instances. Lower values indicate better performance.
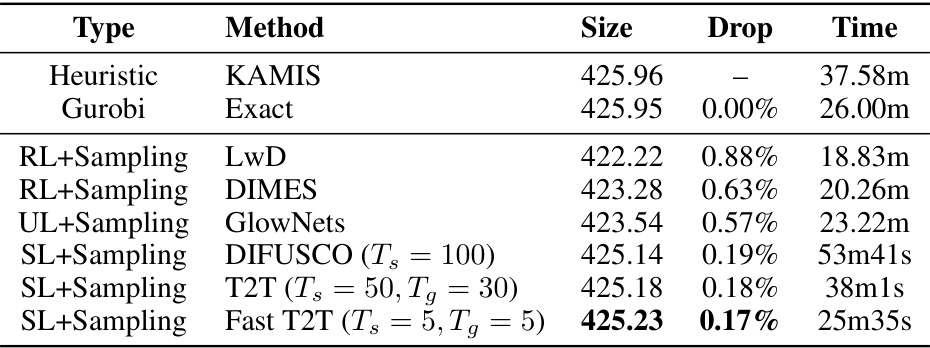
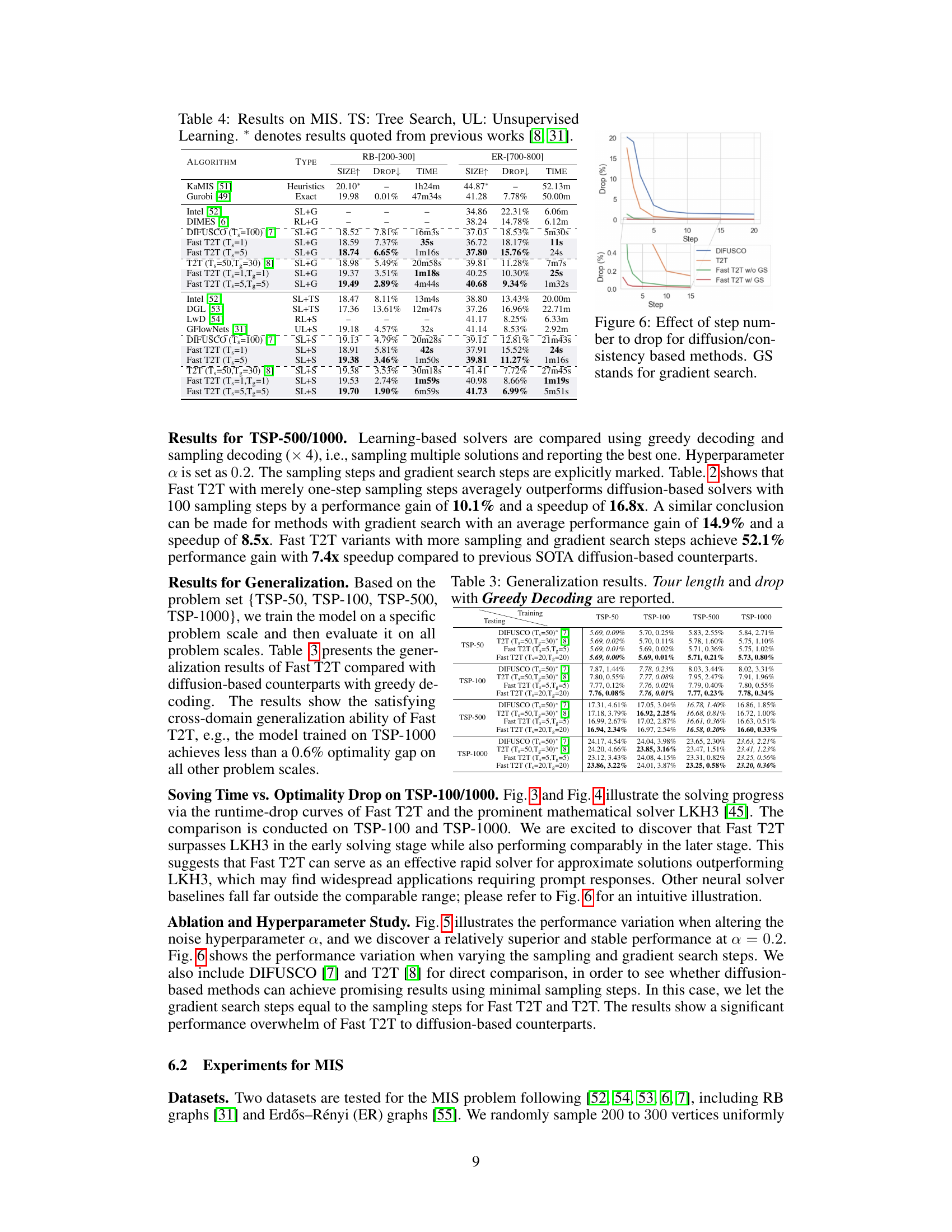
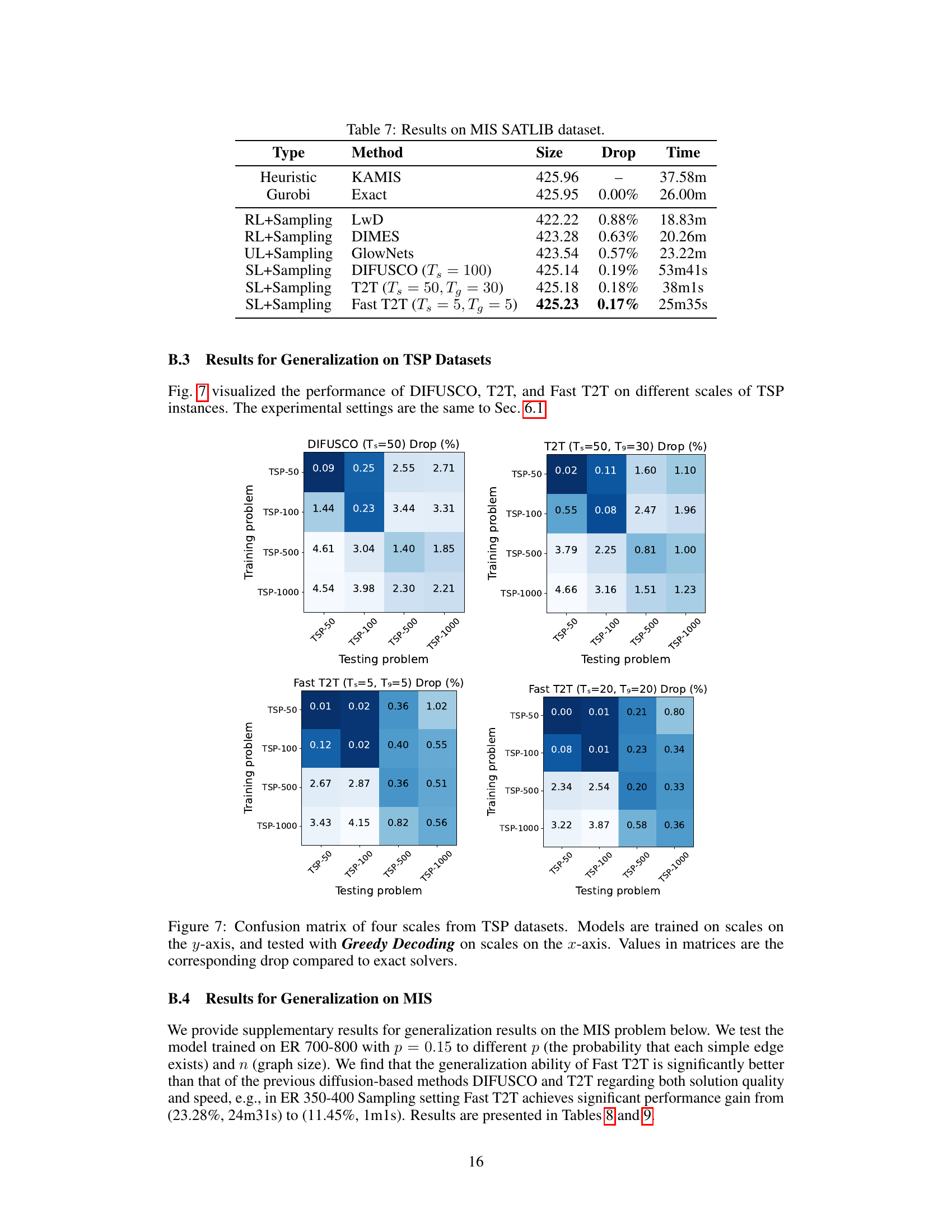
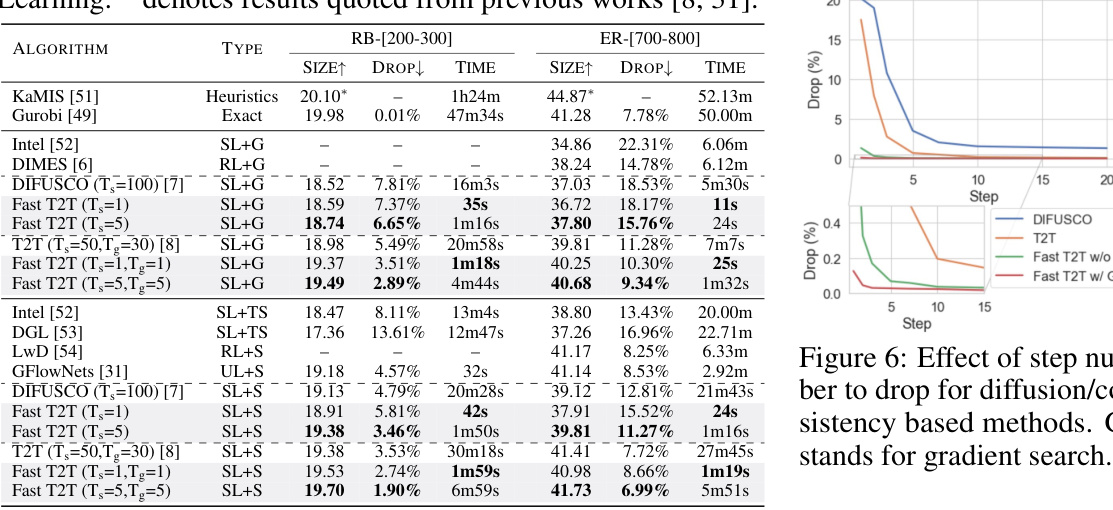
This table presents the results of different methods on the MIS SATLIB dataset. The methods include heuristic methods (KAMIS), an exact solver (Gurobi), and several learning-based methods (LwD, DIMES, GlowNets, DIFUSCO, T2T, Fast T2T). The table shows the size, drop (percentage difference from the optimal solution), and time taken by each method to solve the problem.

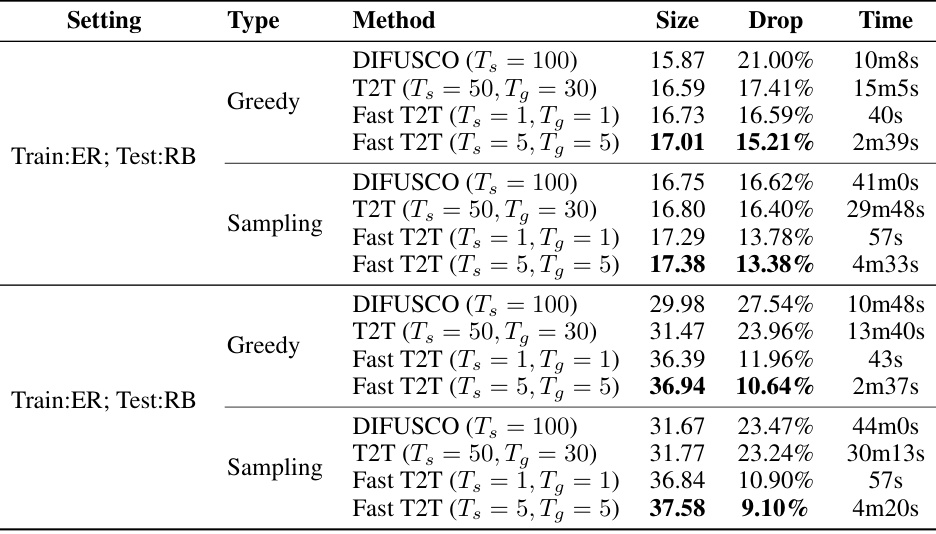
This table presents the generalization performance of different methods (DIFUSCO, T2T, and Fast T2T) on the MIS problem. It shows the size, drop, and time for different values of p (edge probability), which tests the robustness of each method to changes in the input data distribution.
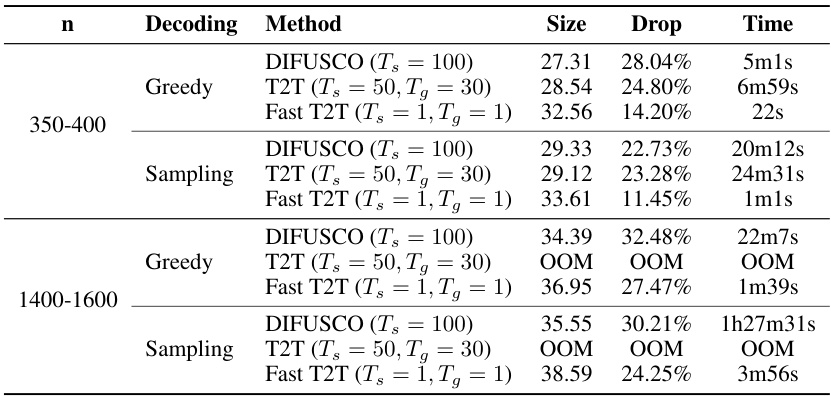
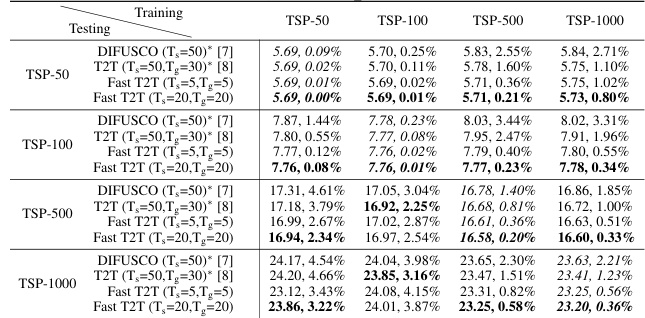
This table presents the experimental results on two larger Traveling Salesman Problem (TSP) instances: TSP-500 and TSP-1000. It compares the performance of Fast T2T against various state-of-the-art methods, including exact solvers (Concorde, Gurobi), heuristics (LKH-3, Farthest Insertion), and other learning-based solvers. The results are presented in terms of solution length (how long the tour is), the percentage drop in solution length from the optimal, and the time taken to find the solution. The table also breaks down the methods by their type (exact, heuristic, reinforcement learning, supervised learning) and decoding strategy (greedy, sampling, beam search) to help readers understand the relative strengths and weaknesses of the approaches. The ‘*’ symbol indicates that some results are taken from previous publications.
This table compares the performance of Fast T2T against various baselines on two larger TSP instances (TSP-500 and TSP-1000). The results show the solution length, optimality drop (percentage difference from the optimal solution), and the solving time. The baselines include exact solvers, heuristics, and other learning-based methods that utilize techniques such as greedy decoding, sampling decoding, beam search, and active search. The table highlights Fast T2T’s superior performance in both solution quality and speed.

This table compares the performance of Fast T2T against various state-of-the-art algorithms on two Traveling Salesperson Problems (TSP) of different sizes (50 and 100 cities). Metrics include solution length, optimality drop (percentage difference from the optimal solution), and solution time. The table shows that Fast T2T achieves competitive or superior results, often with a significantly faster solving time.

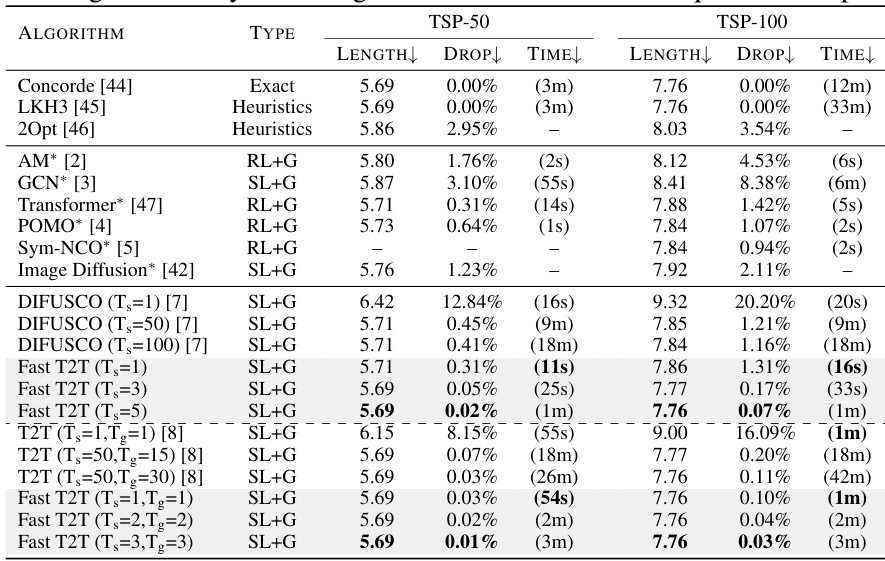
This table shows the hyperparameter ( \alpha ) used for each benchmark problem in the experiments. The ( \alpha ) value is the noise degree used in the training process.
Full paper#