Prospective Learning: Learning for a Dynamic Future

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers dealing with dynamic data and evolving goals, a common challenge in real-world machine learning applications. It provides a novel theoretical framework and algorithm, offering a significant advance over traditional methods that struggle in these scenarios. The framework provides new theoretical foundations and analysis, opening avenues for improving model robustness and predictive accuracy. The practical solutions offered are significant for researchers seeking to develop more robust AI systems.

Visual Insights

#

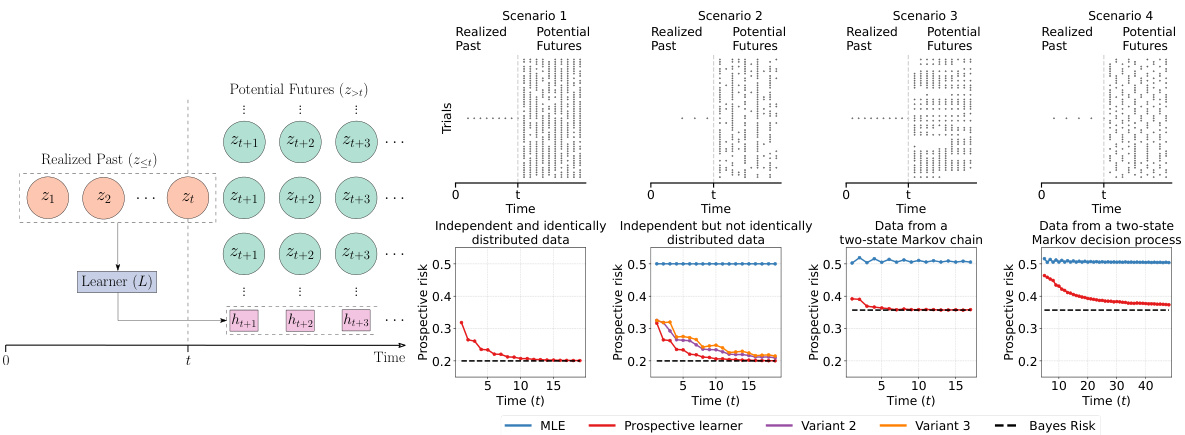
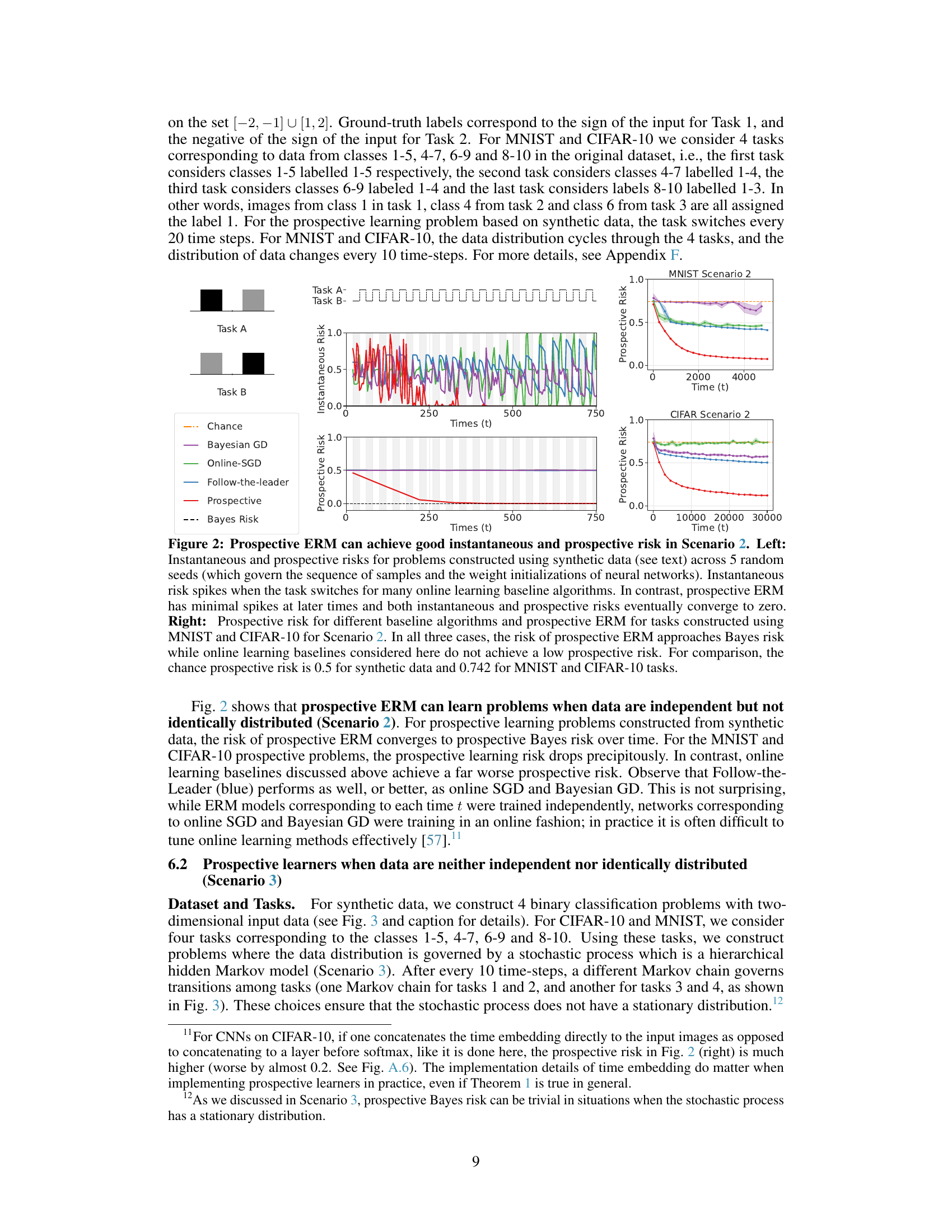
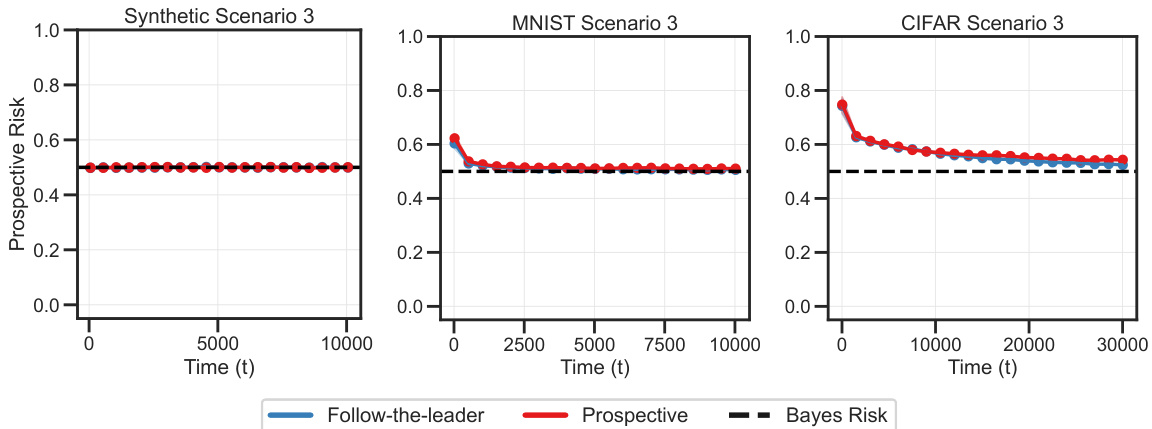
This figure illustrates four different prospective learning scenarios with examples. It visually represents data generation processes (independent and identically distributed, independent but not identically distributed, two-state Markov chain, and two-state Markov decision process), and compares the performance of several learners (MLE, various prospective learners) in terms of their prospective risk over time. The bottom panels show the prospective risk of different learners in each scenario. The goal is to show how prospective learning adapts to changes in the underlying data generating process and its advantage over standard methods.

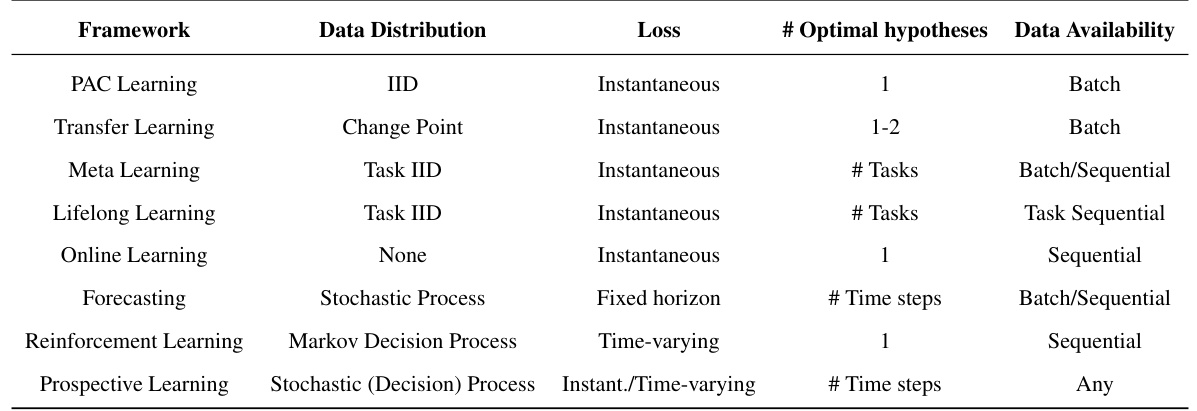
This table compares various machine learning frameworks based on their assumptions about data distribution (IID, change point, task-based, etc.), loss function type (instantaneous or time-varying), number of optimal hypotheses, and data availability (batch, sequential, or any). It highlights the key differences between these approaches, particularly in relation to the novel ‘prospective learning’ framework introduced in the paper. The table serves as a concise summary of existing methods’ characteristics, enabling a clearer understanding of how prospective learning distinguishes itself.

In-depth insights

#

Dynamic Data

#

The concept of ‘Dynamic Data’ in machine learning research is crucial because it acknowledges the ever-changing nature of real-world data. Data distributions shift over time, influenced by trends, user preferences, and external factors. This dynamism directly challenges the fundamental assumptions of traditional machine learning models that often rely on the assumption of independently and identically distributed (i.i.d.) data. A system trained on historical data may not perform well on future data if the underlying distribution has changed significantly. Prospective Learning addresses this challenge head-on by explicitly modeling the temporal dynamics and incorporating the concept of time in the learning process. This approach enables the system to learn from a sequence of hypotheses tailored to predict future data based on past experiences rather than simply attempting to minimize the error based on the current distribution. The core idea is to anticipate future changes in the data and design learning algorithms that continuously update their predictions to remain effective as the environment evolves. This shift in focus from just data to the dynamic process generating the data highlights a significant advancement in designing robust and adaptable machine learning systems.

Prospective ERM

#

Prospective ERM, a novel algorithm introduced in the context of prospective learning, aims to address the limitations of traditional Empirical Risk Minimization (ERM) in dynamic environments. Unlike standard ERM which focuses solely on minimizing past error, Prospective ERM incorporates temporal information to predict future outcomes, thus exhibiting better performance when data distributions or learning goals evolve over time. The core idea is that it learns a sequence of predictors that adapt to changing circumstances, rather than using a single, static predictor. This adaptation is crucial for scenarios where standard ERM would fail, such as those involving non-stationary data or time-dependent optimal hypotheses. The algorithm’s effectiveness is supported by theoretical guarantees of convergence to the Bayes risk under certain assumptions. Furthermore, experimental results demonstrate that Prospective ERM effectively learns various recognition tasks, outperforming other traditional algorithms. Its strength lies in its ability to anticipate future changes, reflecting the core principle of prospective learning that all learning is inherently for the future.

Learning Paradigms

#

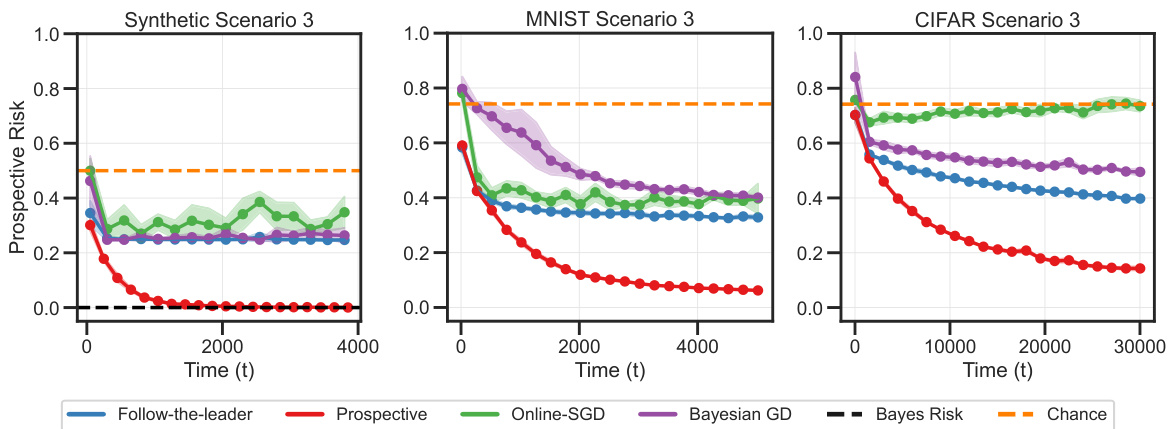
The research paper explores various learning paradigms, comparing and contrasting them with the novel concept of Prospective Learning (PL). PAC learning, with its assumption of independent and identically distributed (IID) data, serves as a baseline, highlighting its limitations in dynamic real-world scenarios. The paper contrasts PL with methods designed to handle distribution shifts, such as domain adaptation, emphasizing that PL tackles evolving distributions and goals far more directly. Multi-task, meta-, continual, and lifelong learning approaches are discussed, with PL differentiated by its focus on prospection – making predictions about an infinite future, rather than simply adapting to the current task or distribution. Online and sequential learning paradigms are considered; while similar in their treatment of sequential data, they differ from PL in their objectives and theoretical underpinnings. Reinforcement learning is examined, noting the key difference that PL emphasizes making predictions rather than taking actions that impact the future. By comparing and contrasting these established methods with PL, the paper establishes the unique theoretical and practical contributions of its prospective learning framework.

Theoretical Limits

#

A theoretical limits analysis for prospective learning would explore the fundamental boundaries of what can be learned about dynamic systems. This would involve investigating the impact of the stochastic process generating the data, including its complexity, stationarity, and ergodicity, on the ability to accurately predict future outcomes. Key questions would include: What are the minimal assumptions needed for consistent learning? How does the complexity of the hypothesis class interact with the stochastic process to determine learnability? Furthermore, it’s critical to analyze the trade-off between computational cost and accuracy in various scenarios. Proving strong or weak learnability under various assumptions, possibly involving discounted future loss or different loss functions, would be pivotal. Ultimately, the goal is to establish rigorous mathematical frameworks for understanding the inherent limits of prediction in dynamic settings and to inform the design of more robust and efficient algorithms.

Future of PL

#

The future of Prospective Learning (PL) is bright, promising significant advancements in machine learning’s ability to handle dynamic real-world scenarios. Addressing the limitations of traditional PAC learning, which assumes static data distributions, PL offers a more robust framework. Future research should focus on developing more efficient algorithms for PL, particularly for complex stochastic processes. Exploring the connections between PL and other learning paradigms, like reinforcement learning and continual learning, is crucial to leverage their strengths. Developing theoretical guarantees for different types of stochastic processes and loss functions will strengthen the foundations of PL. Furthermore, applying PL to diverse real-world problems, such as robotics, healthcare, and climate modeling, will showcase its practical utility and drive further innovation. Addressing challenges in scalability and computational cost associated with handling complex processes is also critical. Finally, exploring the synergy between PL and large language models could yield novel approaches to adaptive and robust AI systems. The integration of temporal dependencies inherent in PL will make AI systems less brittle and more adaptable to real-world changes.

More visual insights

#

More on figures

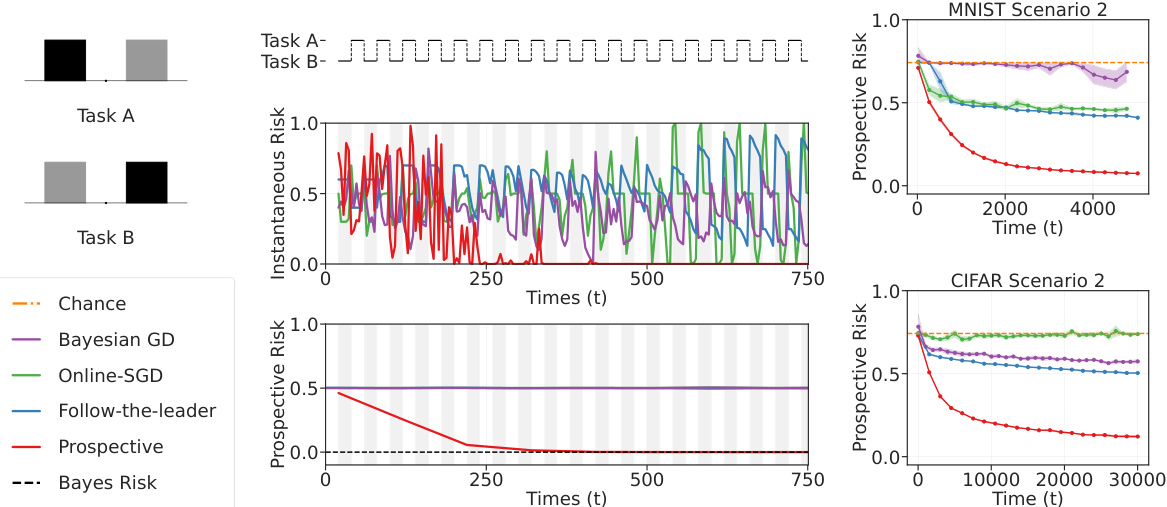
This figure compares the performance of prospective ERM against several online learning baselines on tasks with independently but not identically distributed data (Scenario 2). The left panel shows that prospective ERM achieves consistently low instantaneous and prospective risk, even when the task switches, while online learning baselines exhibit spikes. The right panel further demonstrates the superiority of prospective ERM over baselines on MNIST and CIFAR-10 tasks, showing its convergence towards the Bayes risk.

This figure illustrates four different scenarios of prospective learning, showing how the optimal hypothesis changes over time in each case and comparing the performance of different learning methods. It shows examples of data generation processes, the performance of MLE and prospective learners, and the convergence of their risk towards the Bayes risk.

This figure compares the performance of prospective ERM against several online learning baselines on tasks with independently but non-identically distributed data (Scenario 2). The left panel shows instantaneous and prospective risk curves for a synthetic dataset, highlighting how prospective ERM maintains low risk even during task switches, unlike the baselines. The right panel extends this comparison to MNIST and CIFAR-10 datasets, demonstrating that prospective ERM consistently achieves lower prospective risk, approaching the Bayes risk in all three cases.

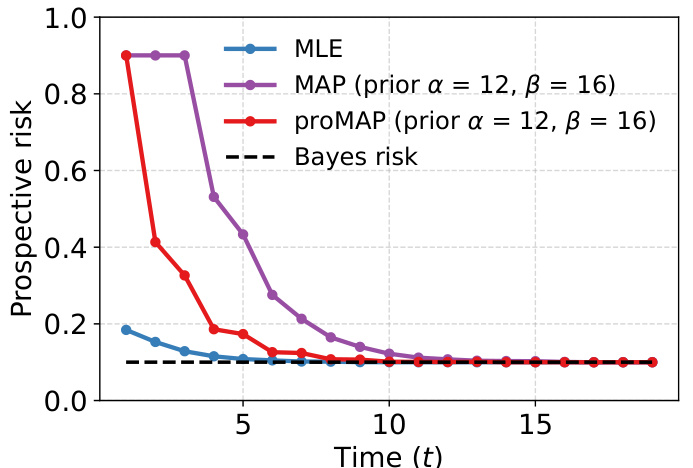
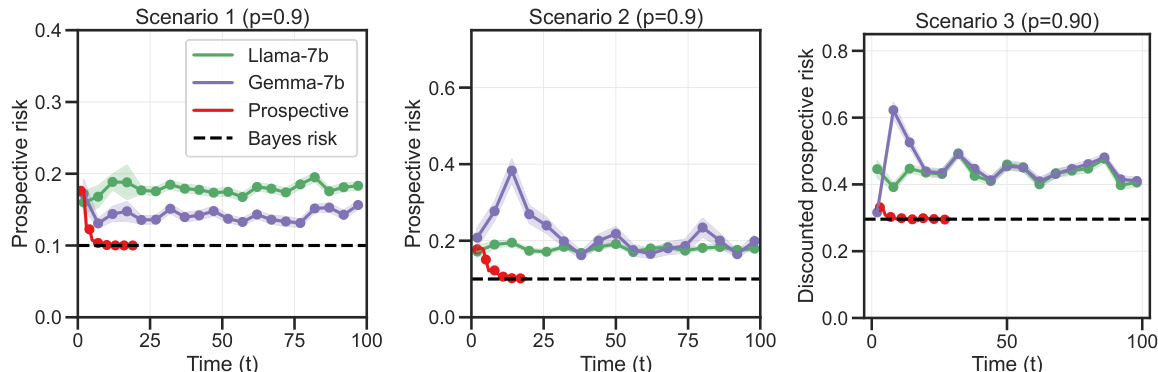
This figure compares the prospective risks of three different learning methods (MLE, MAP, and prospective MAP) under an IID scenario (Scenario 1) with a Bernoulli distribution. The prospective MAP method, which incorporates future predictions into its learning, demonstrates faster convergence to the Bayes risk compared to the traditional MLE and MAP approaches. This highlights the benefit of prospective learning even when data are IID.

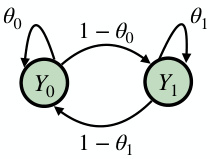
This figure presents a schematic of prospective learning, illustrating its key components: data, hypothesis class, learner, and risk. It also shows example realizations of data for four different scenarios, each with varying degrees of data dependency and distribution shifts, and illustrates the performance of different learners (MLE, prospective learner variants) in each scenario. The figure highlights how prospective learning handles dynamic data distributions and evolving optimal hypotheses.

This figure presents a schematic of prospective learning and examples illustrating four different scenarios. The scenarios highlight how different data distributions and learning approaches affect the learner’s ability to minimize risk, particularly considering the time-dependent nature of optimal hypothesis in prospective learning.

This figure presents a schematic of prospective learning and four different scenarios to illustrate the concept. The scenarios highlight how different data distributions affect the performance of various learning methods, including prospective learning. Each scenario shows example data, and the bottom panels graph the prospective risk of different learning approaches over time. The figure demonstrates how prospective learning can successfully minimize cumulative future risk in dynamic scenarios where standard methods might fail.

This figure illustrates four different prospective learning scenarios. The left panel shows a schematic of the prospective learning process. The top right panel shows example data for each scenario. The bottom panels show the prospective risk of different learners for each scenario. These illustrate that prospective learning can outperform standard methods when dealing with dynamic data.

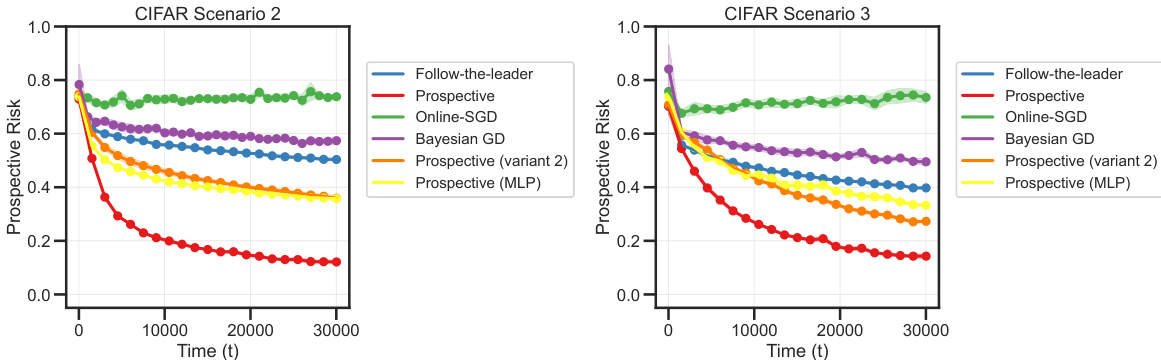
This figure compares the performance of prospective ERM with other online learning algorithms in Scenario 2 (data is independent but not identically distributed). The left panel shows that prospective ERM maintains low risk even when the task switches, unlike other algorithms which experience spikes. The right panel demonstrates that prospective ERM consistently achieves lower prospective risk than other methods across synthetic, MNIST, and CIFAR-10 datasets, approaching the Bayes risk.

This figure illustrates four scenarios of prospective learning with examples. The left panel shows a schematic of prospective learning, while the top-right shows sample data for each scenario. The bottom panels display the performance of different learning methods (MLE, prospective learners) for each scenario, demonstrating how prospective learning can outperform standard methods when the optimal hypothesis changes over time.

This figure illustrates four different prospective learning scenarios with examples. It shows how the optimal hypothesis changes over time in each scenario, and how different learners (including a prospective learner) perform in terms of minimizing the prospective risk. The scenarios range from simple IID data to more complex Markov decision processes.

This figure compares the performance of prospective ERM against other online learning algorithms (Follow-the-leader, Online SGD, Bayesian Gradient Descent) in Scenario 2 (data is independent but not identically distributed). The left panel shows instantaneous and prospective risks for synthetic data, demonstrating that prospective ERM maintains low risk even during task switches, unlike other methods. The right panel shows prospective risk for MNIST and CIFAR-10 datasets, illustrating that prospective ERM consistently achieves lower risk than other algorithms and approaches the Bayes risk.

The figure shows the comparison of prospective ERM and other online learning algorithms like Follow-the-Leader, online SGD, and Bayesian gradient descent in Scenario 2. The left panel shows that prospective ERM achieves better instantaneous and prospective risk than other algorithms when data distribution changes over time. The right panel shows that prospective ERM achieves significantly lower prospective risk compared to other algorithms on MNIST and CIFAR-10 datasets.

This figure illustrates four different scenarios of prospective learning with their corresponding data examples and learner performances. It visually demonstrates how prospective learning handles different levels of data dependency and distribution shifts, contrasting it with standard MLE approaches which perform poorly in dynamic settings. The bottom panels show how the prospective risk of different learners (including variations on prospective ERM) change over time for each scenario.

This figure presents four different scenarios of prospective learning: IID, independent but not identically distributed (INID), Markov Chain, and Markov Decision Process. It visually demonstrates the data distribution for each scenario and shows how different learners (MLE and prospective learners) perform in terms of risk convergence to the Bayes risk over time.

Full paper

#