↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Deep learning models, despite improvements in robustness, remain vulnerable to adversarial attacks. Detecting these vulnerabilities at the individual instance level is crucial for high-stakes applications but computationally expensive using traditional adversarial attack methods. Existing methods to evaluate a model’s robustness are computationally expensive and hinder real-time deployment; evaluating the model’s vulnerability at a per-instance level is therefore intractable and unsuitable for real-time deployment scenarios. This poses significant challenges for deploying these models in safety-critical applications where even small errors can have severe consequences.
This paper introduces the concept of ““margin consistency”” as a solution. Margin consistency connects input space margins and logit margins in robust models, allowing the use of logit margin as an efficient proxy for identifying vulnerable instances. The researchers validate this approach through extensive empirical analysis on CIFAR-10 and CIFAR-100 datasets, demonstrating its effectiveness and reliability. Furthermore, they address cases where margin consistency is not sufficient by learning a pseudo-margin from the feature representation.
Key Takeaways#
Why does it matter?#
This paper is crucial because it offers a novel, efficient way to identify vulnerable model instances without computationally expensive adversarial attacks. This significantly advances the practical deployment of robust models in high-stakes applications, such as autonomous driving and healthcare, where real-time reliability is paramount. It opens up new avenues for research into developing more reliable and safer AI systems.
Visual Insights#
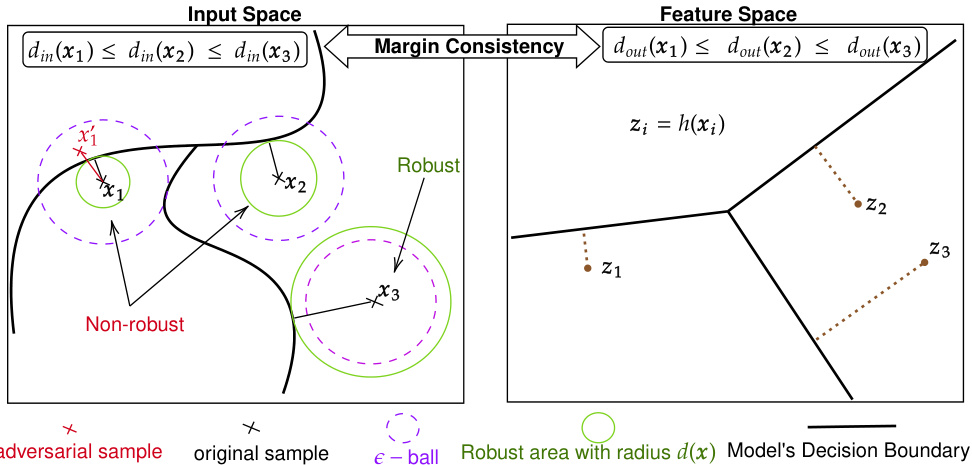
This figure visually represents the concept of margin consistency. The left side shows the input space, where data points (x1, x2, x3) are plotted relative to a decision boundary. Circles around points illustrate the robustness, or distance to the boundary; smaller circles indicate less robustness. The right side shows the corresponding feature space (after the feature extractor). The points (z1, z2, z3) maintain their relative order and distance to the decision boundary, demonstrating margin consistency. If the model were not margin-consistent, the relative positions of the points in feature space would not accurately reflect their robustness in the input space.

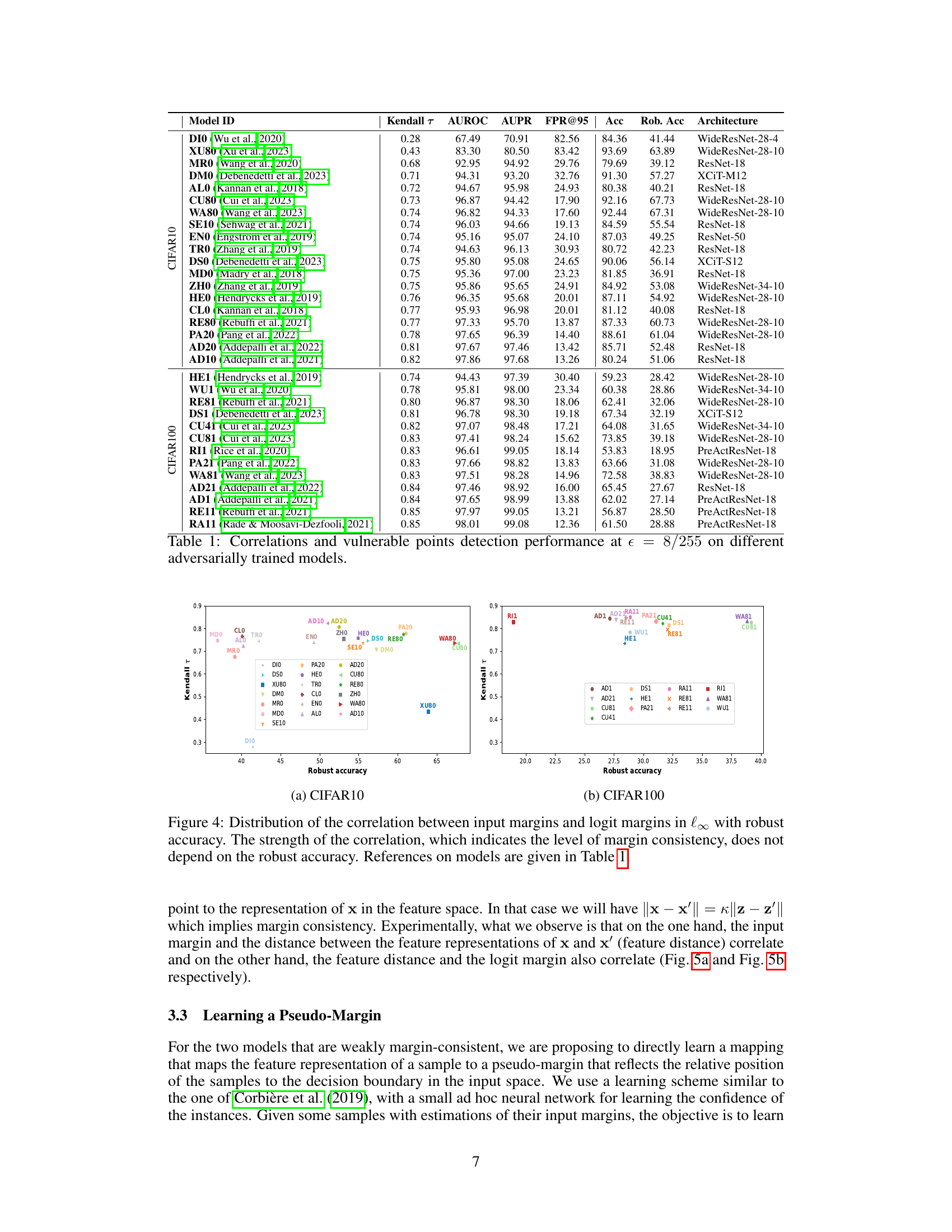
This table presents the results of evaluating various robustly trained models on CIFAR10 and CIFAR100 datasets. The Kendall rank correlation (τ) between the input margin and the logit margin is shown, indicating the level of margin consistency for each model. AUROC, AUPR, and FPR@95 are also provided as metrics for non-robust sample detection, along with the model’s accuracy and robust accuracy. The architecture of each model is also specified. A higher Kendall τ indicates stronger margin consistency, and better performance on the detection task is expected from models with high margin consistency. The table shows that most models exhibit a strong correlation, with the exception of a few.
In-depth insights#
Margin Consistency#
The concept of ‘Margin Consistency’ proposed in the research paper offers a novel approach to efficiently assess the robustness of deep learning models. It posits a strong correlation between a model’s input space margin and its logit margin in robustly trained models. This correlation, termed ‘margin consistency’, implies that the easily computable logit margin can serve as a reliable proxy for the computationally expensive input margin, effectively enabling the identification of vulnerable samples without the need for computationally expensive adversarial attacks. The paper theoretically establishes the necessary and sufficient conditions for this proxy to hold, and empirically demonstrates this correlation across a variety of robust models on CIFAR-10 and CIFAR-100 datasets. This opens the door for efficient, real-time vulnerability detection, crucial for high-stakes applications where directly evaluating the input margin is prohibitive. The study also addresses scenarios where margin consistency is weaker, proposing a method to learn a pseudo-margin from the feature representation to enhance the reliability of the logit margin as an indicator of vulnerability.
Robustness Detection#
Robustness detection in deep learning models is crucial for reliable real-world deployment, especially in high-stakes applications. Current methods often rely on computationally expensive adversarial attacks to evaluate instance-level vulnerability, hindering real-time applications. This research proposes a novel approach by leveraging margin consistency, a relationship between input and logit margins in robust models. The core idea is that a model’s logit margin can effectively approximate its input margin, providing a computationally efficient proxy for identifying non-robust samples. This is supported by empirical analysis showcasing a strong correlation between these margins across various robustly trained models. For models lacking sufficient margin consistency, the study suggests learning a pseudo-margin from feature representations to enhance the accuracy of vulnerability detection. The significance lies in the efficiency and scalability of this approach, enabling real-time assessment of model robustness without the heavy computational demands of conventional adversarial attacks.
Pseudo-margin Learning#
The concept of ‘pseudo-margin learning’ in the context of robust deep learning addresses the challenge of efficiently detecting vulnerable data points by learning a surrogate margin from the model’s feature representation. When a model lacks sufficient ‘margin consistency’, meaning the relationship between the input space margin and logit margin is weak, directly using the logit margin to detect non-robust samples becomes unreliable. Therefore, pseudo-margin learning aims to create a new margin metric that strongly correlates with the actual input space margin. This is achieved through training a simple mapping network that takes the model’s high-level features as input and outputs a pseudo-margin score that accurately reflects how far a sample is from the decision boundary in the input space. This approach essentially simulates margin consistency, enabling reliable vulnerability detection even in models that originally lack this property. The effectiveness of pseudo-margin learning is demonstrated by improved correlation between the learned pseudo-margin and the true input margin, and ultimately enhances the performance of non-robust sample detection.
Limitations and Scope#
The research primarily focuses on local robustness evaluated through the lens of the input space margin, a limitation that prevents a full understanding of the model’s robustness to adversarial attacks. The reliance on attack-based estimation for input margin verification introduces uncertainty, especially if a model proves difficult to attack. The study’s scope is limited by its focus on l∞ robustness, neglecting other p-norms which could reveal different vulnerabilities. The assumption of margin consistency is crucial to the approach, but its validity might not hold universally. Neural collapse, a phenomenon occurring in deep learning models, could affect margin consistency, making conclusions potentially less generalizable. Finally, the detection method’s effectiveness is not fully explored with respect to adaptive attacks and different data distributions beyond the training set. Addressing these limitations will offer a more robust and comprehensive perspective on model robustness.
Future Directions#
Future research could explore extending the margin consistency concept to other robustness metrics beyond the l∞ norm, potentially encompassing l1 and l2 norms. Investigating the relationship between margin consistency and different adversarial training techniques would be valuable, potentially revealing optimal training strategies for enhancing both accuracy and robustness. Furthermore, research on the impact of neural collapse on margin consistency is crucial. As models approach neural collapse, the relationship between input and logit margins may change, affecting the efficacy of the proposed method. Finally, developing more sophisticated methods to approximate input margins and address cases of low margin consistency is warranted. This could involve exploring alternative methods or integrating additional information, such as uncertainty estimates. By combining these insights, researchers can significantly improve the reliability and efficiency of non-robust sample detection for real-world applications.
More visual insights#
More on figures
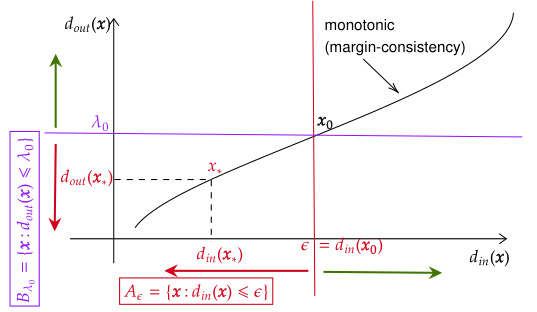
This figure visually explains the concept of margin consistency. It shows two spaces: the input space and the feature space. In the input space, the distance from a sample to the decision boundary is called the input margin. Samples closer to the boundary are less robust and more likely to be misclassified by adversarial attacks. The feature space represents the output of a feature extractor (e.g., penultimate layer of a deep neural network) applied to the input samples. The distance from a sample’s feature representation to the decision boundary in this space is the feature margin. Margin consistency means that the relative order of samples based on input margins is preserved in the feature space. If a sample has a smaller input margin than another, it will also have a smaller feature margin. This property is crucial because it allows the use of the easily computable feature margin (logit margin) as a proxy for the computationally expensive input margin in order to efficiently detect vulnerable samples.

This figure illustrates the proof of Theorem 1, which establishes the relationship between margin consistency and the ability to use the logit margin to separate robust and non-robust samples. Panel (a) shows that with margin consistency (a monotonic relationship between input margin and logit margin), a threshold on the logit margin can perfectly separate robust and non-robust samples. Panel (b) demonstrates that without margin consistency, such a separation is not possible, highlighting the necessity of margin consistency for reliable non-robust sample detection using the logit margin.
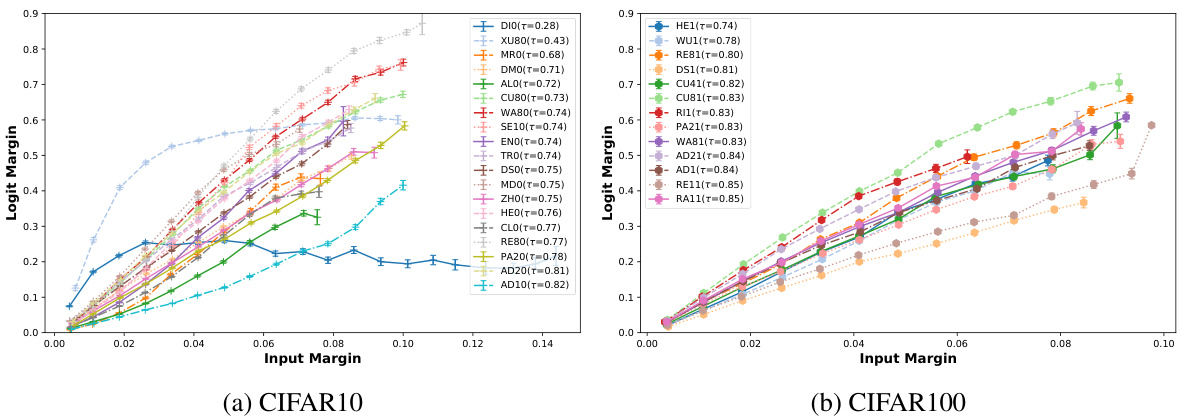
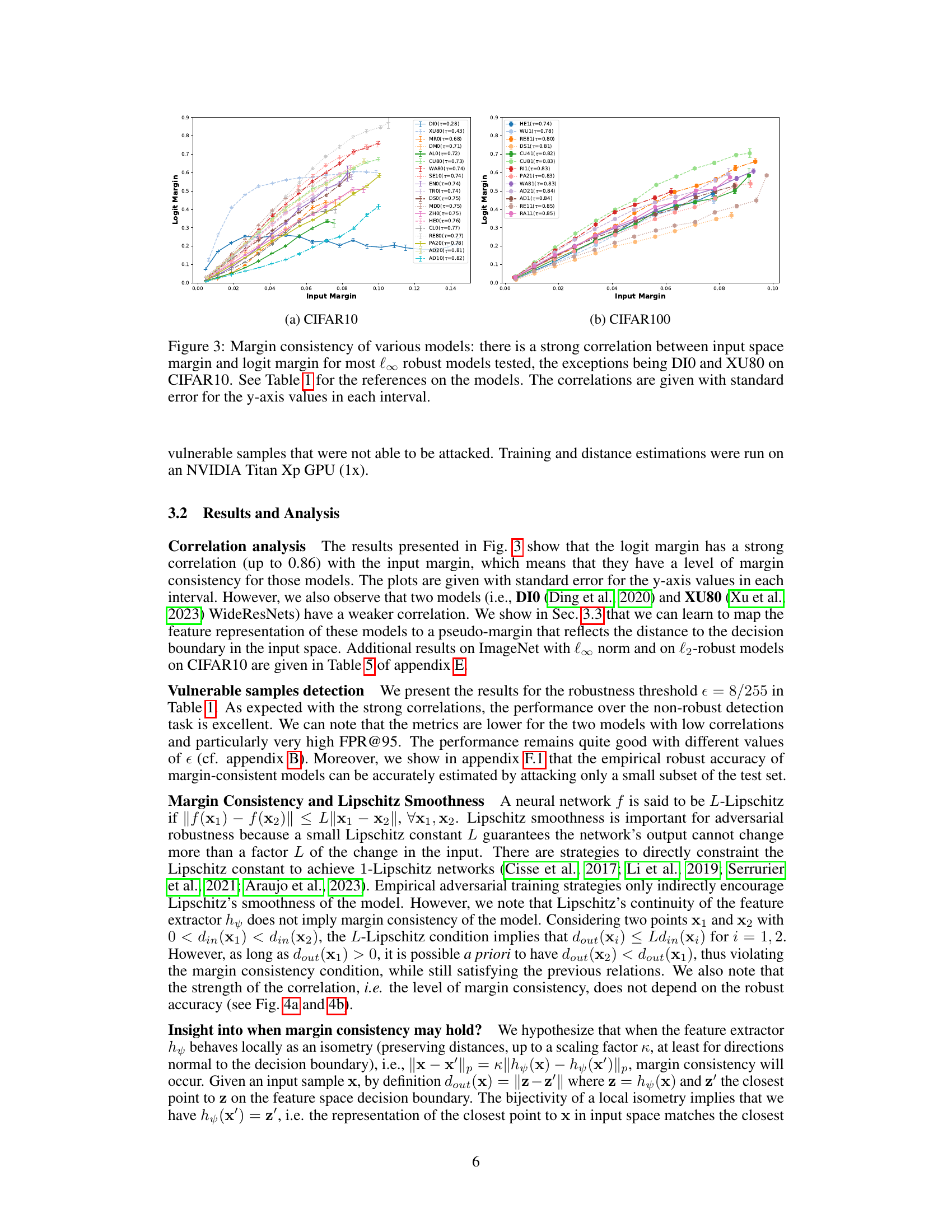
This figure shows the strong correlation between input space margin and logit margin for various robust models tested on CIFAR10 and CIFAR100 datasets. The x-axis represents the input margin and the y-axis represents the logit margin. Each line corresponds to a different model, and the Kendall rank correlation coefficient (τ) is provided for each model. Most models show a strong positive correlation, indicating margin consistency, with the exceptions of DIO and XU80 on CIFAR10, which have weaker correlations. This suggests that the logit margin can be used effectively as a proxy for the input margin in most robust models for identifying vulnerable samples.

This figure displays the margin consistency of various robust models by plotting the logit margin against the input margin for each model on the CIFAR10 and CIFAR100 datasets. The strong correlation (except for DIO and XU80 on CIFAR10) between input and logit margins demonstrates that the models preserve the relative positions of samples to the decision boundary between the input and feature spaces. This is a key finding of the paper, supporting the use of logit margin as a proxy for input margin in non-robust sample detection.
This figure shows the relationship between input space margin and logit margin for various robust models on CIFAR10 and CIFAR100 datasets. The x-axis represents the input space margin, and the y-axis represents the logit margin. Each line represents a different model, and the Kendall rank correlation (τ) is shown for each model. Most models show a strong positive correlation (high margin consistency), indicating that the logit margin is a good proxy for the input margin. However, some models (DIO and XU80 on CIFAR10) show weak correlations (low margin consistency), suggesting that the logit margin may not be a reliable estimate of the input margin for these models.
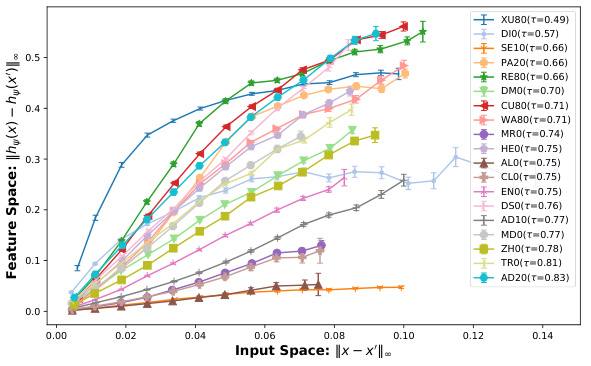
This figure shows the correlations between three different metrics: input margin, feature distance, and logit margin. It visually represents the relationships between these metrics across various models, suggesting that the local isometry (preservation of distances) of the feature extractor plays a significant role in margin consistency. The correlations (with standard errors) are displayed for each model, providing insight into how well the feature space reflects the input space regarding the distance to the decision boundary. Table 1 is referenced to identify the specific models involved.

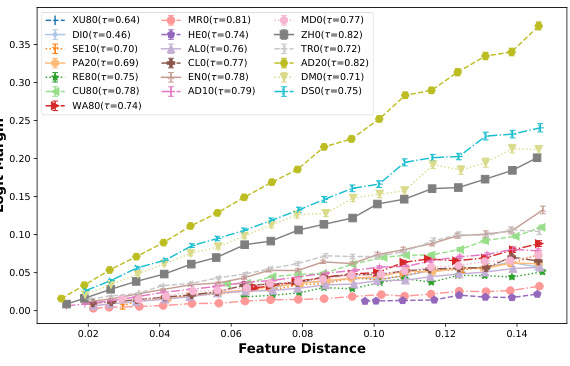
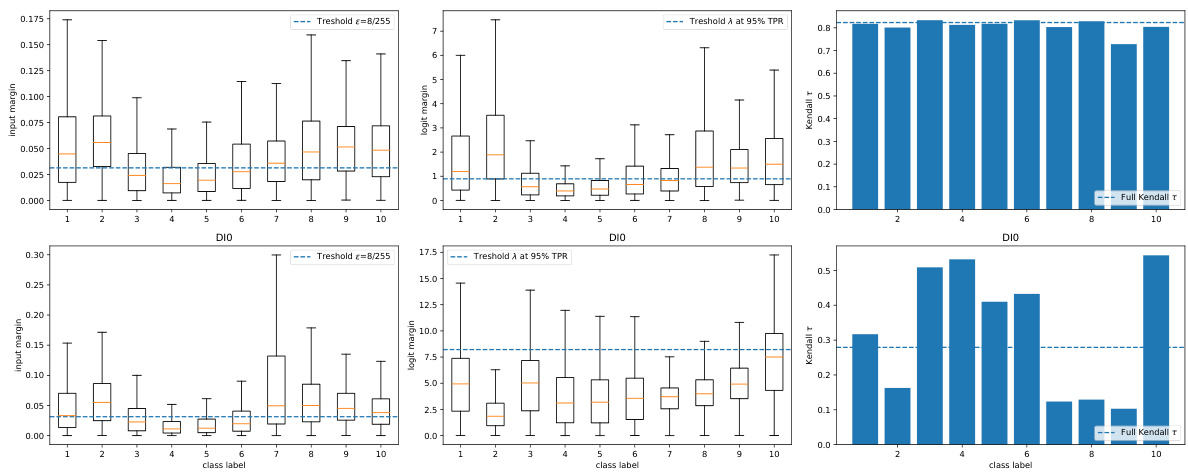
This figure displays the correlation improvement achieved by learning a pseudo-margin over using only the logit margin for two models, DI0 and XU80, that exhibit weak margin consistency. The x-axis represents the input margin, and the y-axis shows the margin (either logit margin or learned pseudo-margin). The plots demonstrate that learning a pseudo-margin significantly improves the correlation between the input and feature space margins for these models. Kendall’s tau and the false positive rate at 95% true positive rate (FPR@95) are provided for both the logit margin and the learned pseudo-margin to quantify the improvement.

This figure shows the performance of the non-robust sample detection for various values of robustness threshold (epsilon). The plots show AUROC and AUPR curves for different epsilon values. The results demonstrate that even with varying thresholds, the high margin consistency of the models allows the logit margin to serve as a good proxy for the detection task.
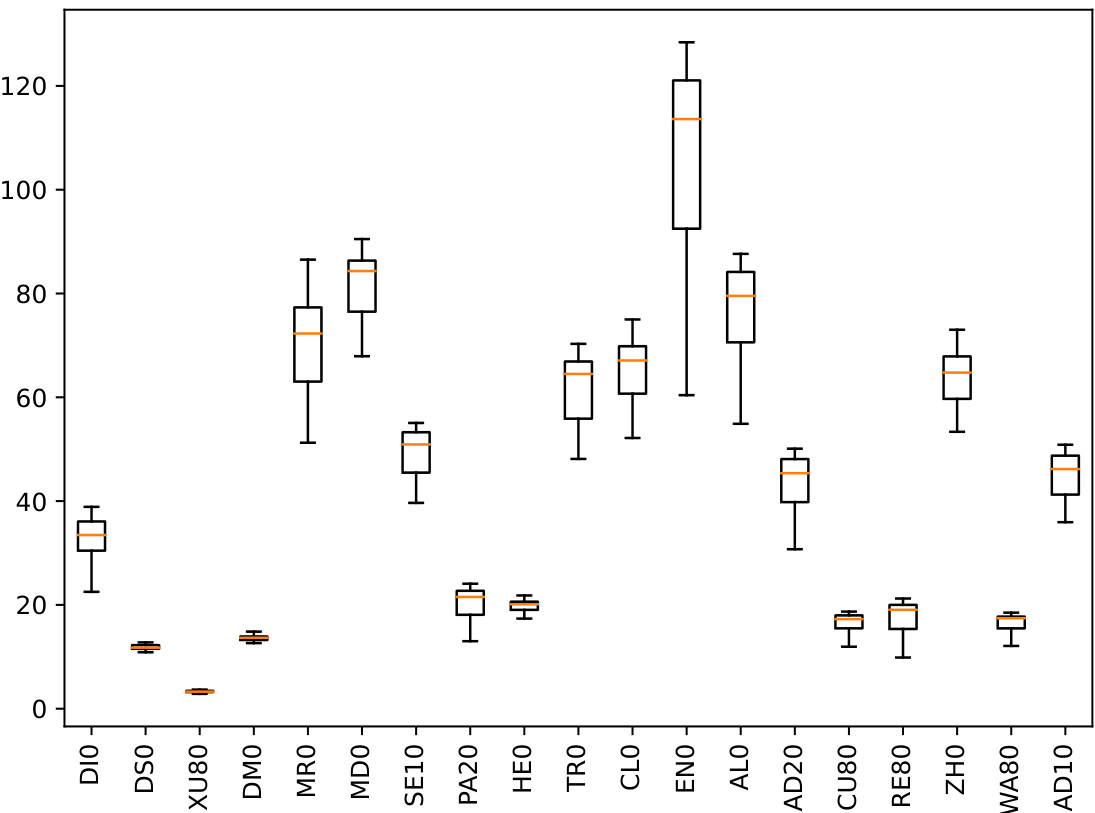
This boxplot shows the distribution of distances between pairs of linear classifiers for CIFAR10 models. The distances are calculated as the norm of the weight difference between each pair of classifiers. The plot displays the minimum, first quartile (Q1), median, third quartile (Q3), and maximum values for the distribution of distances across all model pairs. It helps visualize the level of equidistance among the classifiers, which is a factor related to margin consistency.
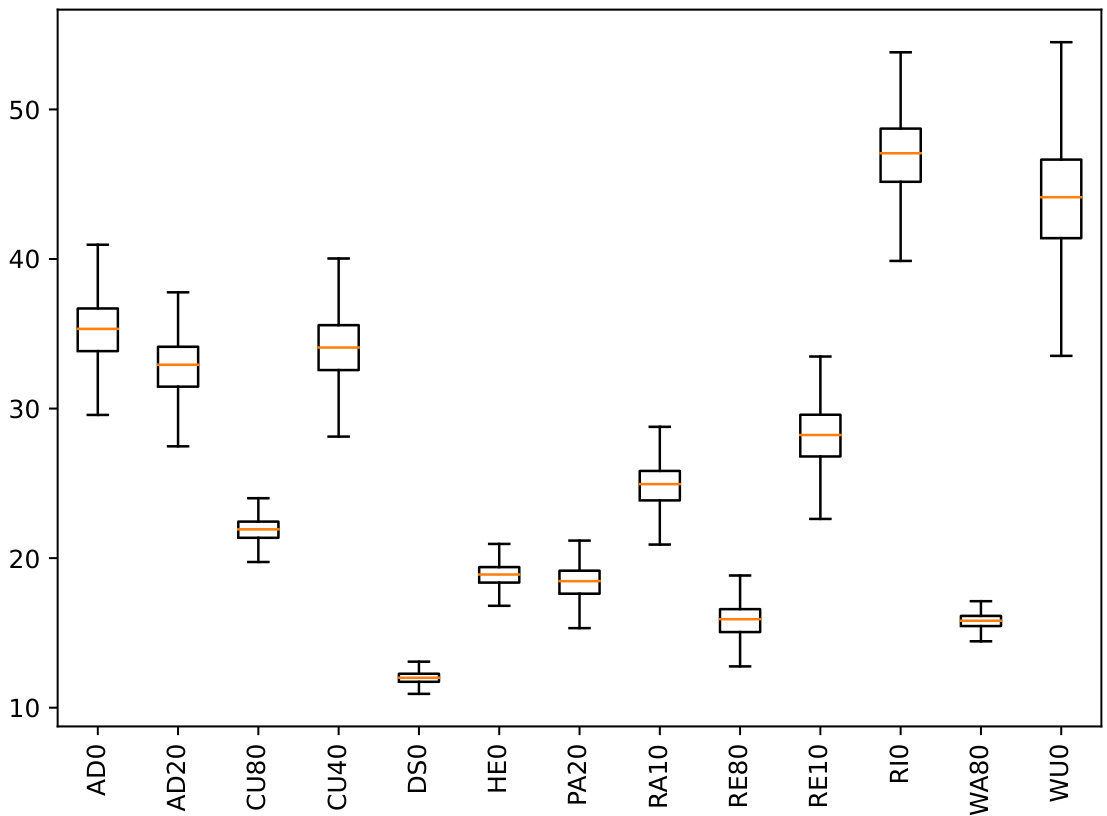
This figure shows boxplots visualizing the distribution of distances between pairs of linear classifiers for various CIFAR10 models. The boxplot for each model displays the minimum, first quartile (Q1), median, third quartile (Q3), and maximum distances. This visualization helps assess the assumption of equidistance between linear classifiers, which is relevant for the logit margin approximation of input space margin in margin-consistent models.

This figure displays the results of estimating robust accuracy using only a subset of 500 samples instead of the full test set. It compares the robust accuracy estimated using the logit margin against the robust accuracy obtained with the full AutoAttack. The results show that for strongly margin-consistent models, the estimations are highly accurate, demonstrating the efficiency of using logit margins as a proxy for robust accuracy.
This figure shows the variation of the AUROC (Area Under the Receiver Operating Characteristic curve) and AUPR (Area Under the Precision-Recall curve) scores with different values of the robustness threshold (epsilon). It demonstrates how well the model can discriminate between robust and non-robust samples for various robustness thresholds. The AUROC and AUPR scores are metrics that evaluate the performance of the model in distinguishing between these two classes of samples. A higher value indicates better performance.
More on tables

This table compares the performance of using the logit margin versus the learned pseudo-margin for non-robust sample detection. It shows that the learned pseudo-margin significantly improves the correlation between the margin in the input space and the margin in the feature space, resulting in better performance for non-robust sample detection as measured by AUROC, AUPR, and FPR@95.

This table presents the Kendall rank correlation (τ), AUROC, AUPR, FPR@95, accuracy (Acc), and robust accuracy (Rob. Acc) for various adversarially trained models on CIFAR10 and CIFAR100 datasets. The models used represent diverse adversarial training strategies. The table also indicates the architecture of each model. This data is used to evaluate the performance of the logit margin as a proxy for input margin in identifying vulnerable samples, highlighting model margin consistency.
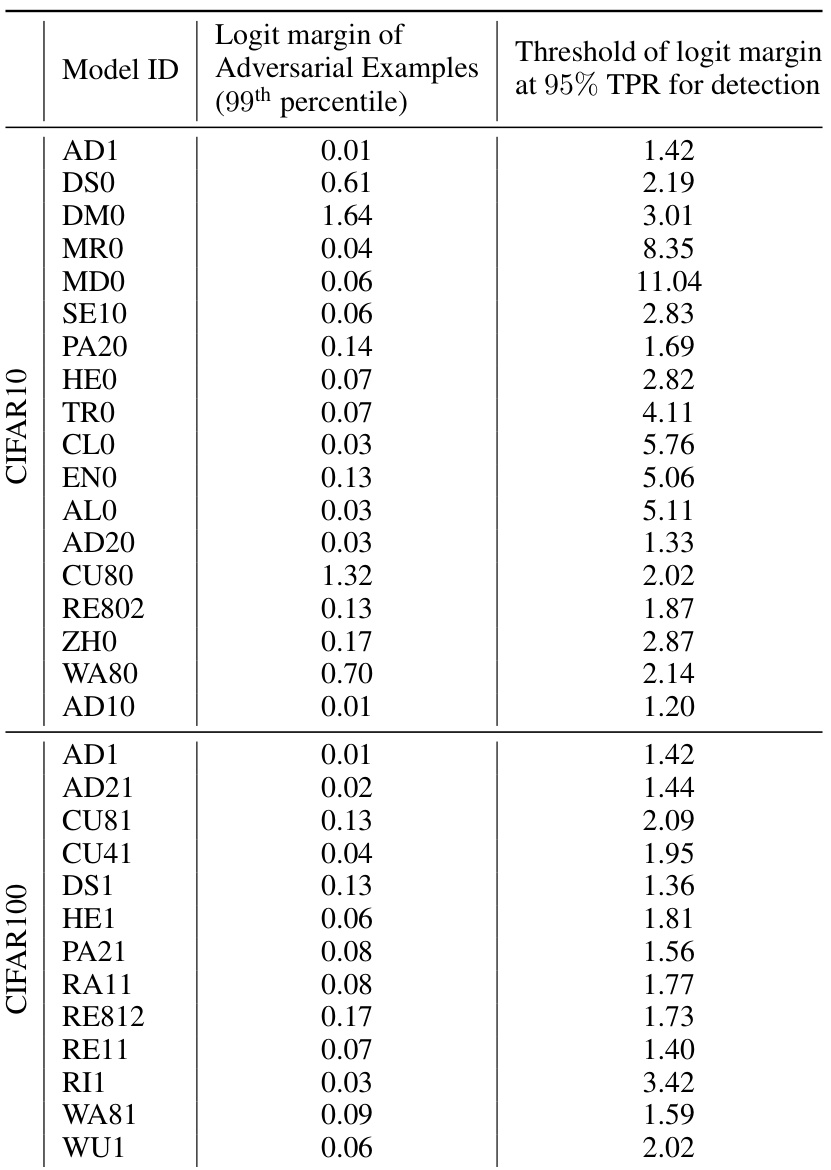
This table presents the Kendall rank correlation (τ), AUROC, AUPR, FPR@95, accuracy, and robust accuracy for various adversarially trained models on the CIFAR10 and CIFAR100 datasets. The models represent different adversarial training strategies. The robust accuracy is evaluated using AutoAttack. The Kendall tau correlation is a measure of the monotonic relationship between the input space margin and the logit margin, which is central to the paper’s proposed method for detecting vulnerable samples.

This table presents the results of evaluating various adversarially trained models’ performance on two tasks: Kendall’s tau correlation between input and logit margins and non-robust sample detection. The table includes model IDs, Kendall tau correlation values, AUROC, AUPR, FPR@95 (False Positive Rate at 95% True Positive Rate), accuracy, and robust accuracy. It also specifies the architecture used for each model. The results are calculated using a robustness threshold of (\epsilon = 8/255). The table allows for comparing the margin consistency (correlation) and the non-robust sample detection capability of the different models.
Full paper#