↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Generating high-fidelity samples from diffusion models is computationally expensive, often requiring hundreds of sequential model evaluations, which limits their use in real-time applications. Current methods either reduce steps, sacrificing quality, or use parallel-in-time methods with memory limitations. This creates a need for faster and more efficient sampling techniques.
This paper introduces Self-Refining Diffusion Samplers (SRDS), a novel method inspired by the Parareal algorithm that leverages parallelization to speed up sample generation. SRDS generates a quick, rough sample estimate, then iteratively refines it in parallel, maintaining high-quality outputs. The technique is approximation-free, broadly compatible with solvers, and showcases significant speed improvements, reaching up to 4.3x faster generation on certain benchmarks. This opens avenues for real-time applications previously hindered by computational costs.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in AI and related fields due to its significant advancements in diffusion model sampling. By enabling parallelization without sacrificing sample quality, it accelerates the generation process substantially. This is particularly relevant given the increasing computational demands of high-fidelity generative models. The approximation-free nature of the proposed algorithm and its broad compatibility with existing solvers expand its potential impact, opening doors for extensive further research and optimization.
Visual Insights#

This figure shows how the Self-Refining Diffusion Sampler (SRDS) algorithm iteratively refines a sample generated by Stable Diffusion. Starting from a rough estimate (leftmost image) produced with fewer steps, the algorithm progressively improves the quality of the sample through parallel iterations, with the third iteration showing almost perfect convergence to the final, high-quality image.

This table presents the FID scores achieved by the Self-Refining Diffusion Samplers (SRDS) algorithm on four different image datasets: LSUN Church, LSUN Bedroom, Imagenet, and CIFAR. For each dataset, the table shows the FID score obtained using a standard sequential DDIM solver, and the FID score and various computational metrics obtained using the SRDS algorithm. The computational metrics include the number of SRDS iterations, the effective number of serial model evaluations (considering parallel evaluations as one), and the total number of model evaluations performed by SRDS. Lower FID scores indicate better image quality.
In-depth insights#
Parareal’s Diffusion#
The concept of “Parareal’s Diffusion” blends the Parareal algorithm, known for its parallel-in-time integration capabilities, with the iterative refinement process inherent in diffusion models. Parareal’s strength lies in decomposing a temporal problem into smaller, independent subproblems, solved concurrently. In the context of diffusion sampling, this could mean parallelizing the multiple denoising steps required to generate a sample. This approach, if effective, would drastically reduce the latency of diffusion models, making them more suitable for real-time applications. The core idea is to perform a quick, coarse estimation of the sample first, then iteratively refine this estimate in parallel. A key challenge would be ensuring the accuracy of the parallel approach, guaranteeing convergence to the same result as a sequential, high-fidelity computation. The success of “Parareal’s Diffusion” depends heavily on the nature of the diffusion model’s ODE, solver choice, and the efficiency of the parallel computation. It offers a potentially powerful path towards faster diffusion sampling, but careful analysis and design are needed to avoid trade-offs in sample quality and to manage computational resource usage.
SRDS: Parallel ODE#
The heading ‘SRDS: Parallel ODE’ suggests a novel approach to solving ordinary differential equations (ODEs) within the framework of Self-Refining Diffusion Samplers (SRDS). SRDS likely leverages the inherent iterative nature of ODE solvers to enable parallelization, potentially achieving significant speedups in generating samples from diffusion models. This could involve techniques like the Parareal algorithm, which partitions the time domain and solves subproblems concurrently. A key challenge would be balancing the computational overhead of parallelization with the accuracy of the ODE solution. The approach likely focuses on achieving a balance, refining a coarser initial estimate through parallel iterations to converge to a high-fidelity solution, making it computationally efficient while maintaining high sample quality. The parallelisation could lead to improved inference speed for applications like image generation, allowing for real-time or near real-time processing. However, scalability across different hardware architectures and the memory requirements of parallel processing are critical factors that would need careful consideration in the design of SRDS.
SRDS Convergence#
The SRDS (Self-Refining Diffusion Samplers) convergence behavior is a crucial aspect of its efficiency and accuracy. SRDS leverages the Parareal algorithm, iteratively refining a coarse initial sample in parallel to reach a high-fidelity solution. This iterative refinement process is shown to converge quickly, significantly reducing the number of steps needed compared to traditional methods. The paper demonstrates this with experiments, showing fast convergence on various benchmarks and pre-trained diffusion models such as Stable Diffusion. A theoretical convergence guarantee is provided, assuring that SRDS will always converge to the correct solution within a bounded number of iterations. This guarantee, along with empirical observations of even faster convergence in practice, highlights the method’s robustness and reliability. The speed of convergence is influenced by factors such as the choice of coarse and fine solvers, the tolerance threshold, and the length of the diffusion trajectory. Understanding and optimizing these factors are vital for maximizing SRDS’s performance in real-world applications. Early convergence is particularly beneficial for reducing latency, making SRDS suitable for time-sensitive tasks and real-time applications that were previously impractical with slower diffusion samplers. The approximation-free nature of SRDS ensures that this speed comes without sacrificing the quality of the generated samples.
SRDS: Tradeoffs#
SRDS, while offering significant speedups in diffusion sampling, involves inherent trade-offs. The primary trade-off is between computational cost and speed. Achieving faster sampling times requires more parallel computation, increasing the total number of model evaluations compared to sequential methods. This means SRDS might not be the most efficient choice for applications severely constrained by computational budgets. However, the approximation-free nature of SRDS ensures high-quality samples are maintained, unlike methods that sacrifice sample fidelity for speed. The algorithm’s flexibility allows practitioners to balance speed and quality by adjusting parameters and the number of iterations. The degree of parallelism is another aspect: more GPUs facilitate faster convergence, but this introduces additional hardware costs. Ultimately, the optimal use of SRDS depends on careful consideration of available resources, desired sample quality, and the specific application needs. The balance between parallel computation, quality preservation, and application requirements forms the core trade-off in SRDS.
Future of SRDS#
The future of Self-Refining Diffusion Samplers (SRDS) is promising, building upon its current strengths and addressing limitations. Convergence guarantees, currently limited, need further theoretical exploration to broaden applicability. While SRDS demonstrates impressive speedups, optimizing the balance between parallel compute and sample quality remains an important area for development. This could involve exploring adaptive methods that adjust the number of iterations based on the desired fidelity. Extending SRDS to other diffusion models and solvers beyond those tested warrants investigation, enhancing its versatility and utility across various generation tasks. Furthermore, research should examine ways to mitigate the increased computational cost of SRDS, perhaps by developing more efficient coarse solvers or leveraging specialized hardware. Finally, exploring the potential of integrating SRDS with other acceleration techniques like quantization or distillation could unlock even faster and higher-quality sampling, opening exciting possibilities for real-time applications and interactive experiences with diffusion models.
More visual insights#
More on figures
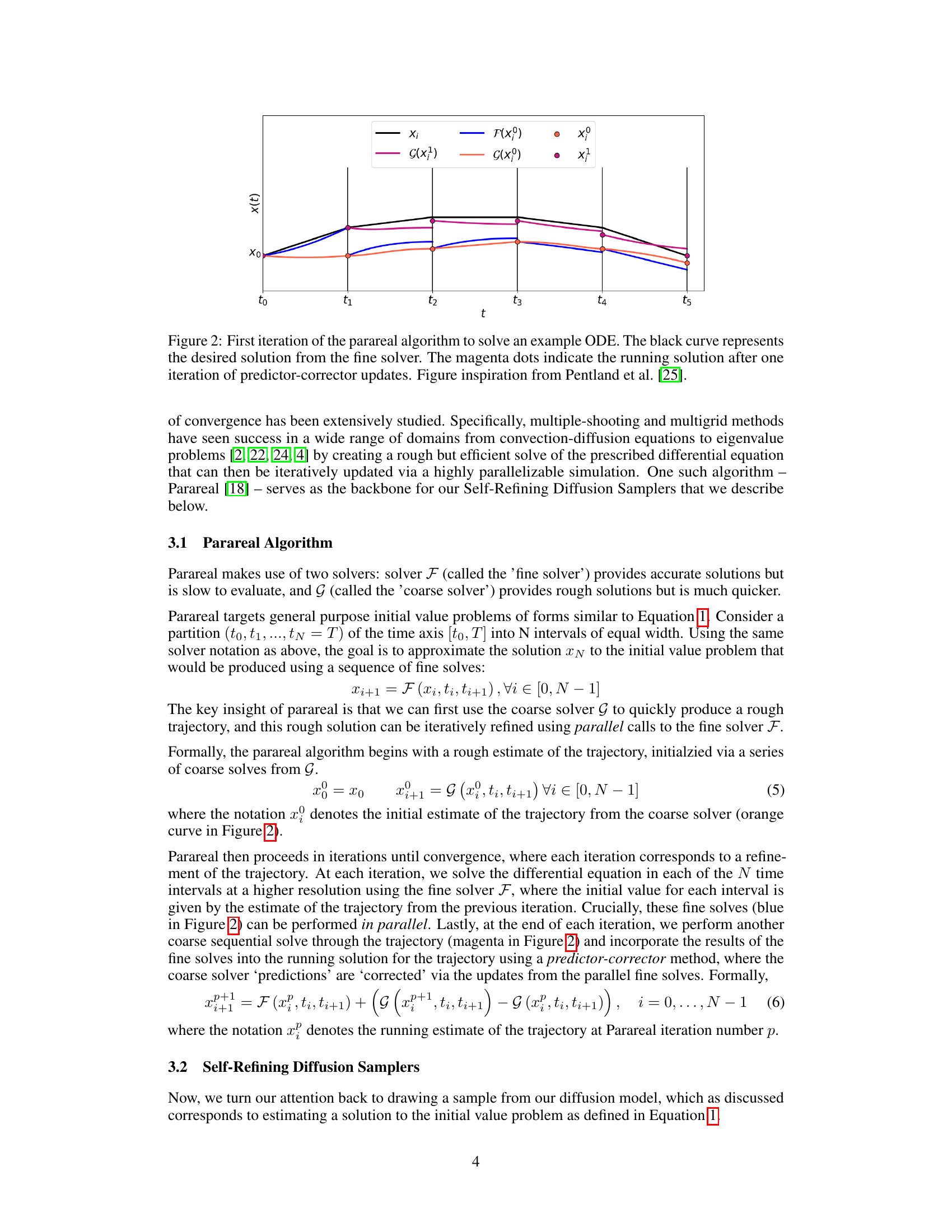
This figure illustrates the first iteration of the Parareal algorithm, a parallel-in-time integration method. The black curve shows the exact solution obtained using a computationally expensive ‘fine’ solver. The orange curve is a rough initial estimate of the solution from a fast ‘coarse’ solver. The algorithm then refines this estimate in parallel using the fine solver on subintervals and updates using a predictor-corrector mechanism. The magenta dots show the improved solution after the first iteration. The process is repeated until convergence to the exact solution.
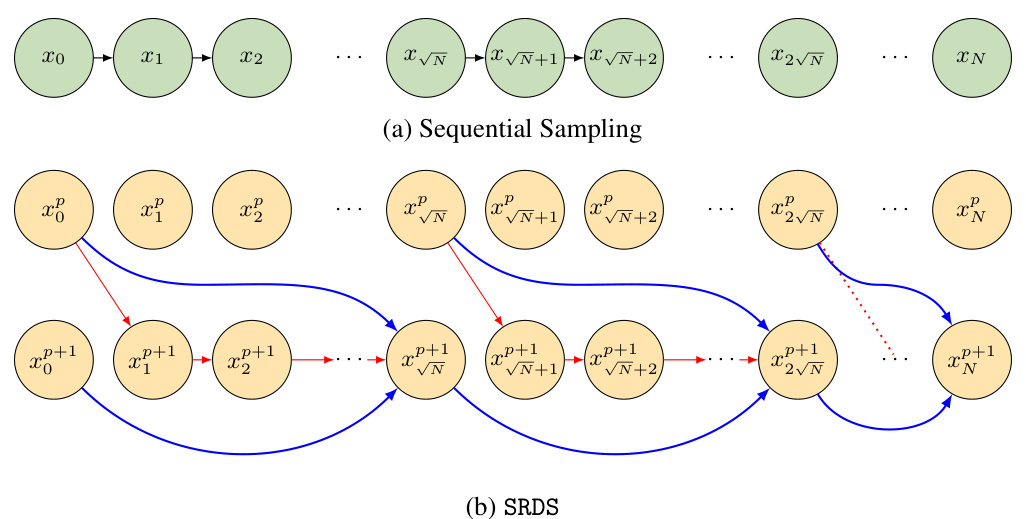
This figure illustrates the computational difference between sequential sampling and the proposed SRDS algorithm. Sequential sampling (a) shows a linear chain of computations, where each step depends on the previous one. In contrast, SRDS (b) employs a parallel-in-time approach. It starts with a coarse estimation of the entire trajectory (yellow nodes), which is then refined iteratively using parallel fine solves (red arrows) in blocks. The fine solves within a block are independent of each other, thus allowing parallelization. Blue arrows represent coarse solves, which update the overall trajectory after each parallel fine solve iteration. The dotted red line in (b) indicates convergence where additional iterations would not significantly change the result.

This figure illustrates how pipelining in SRDS leads to a 2x speedup. The top shows the non-pipelined version, where each iteration of the algorithm completes before the next begins. The bottom shows the pipelined version. The fine solves (red arrows) in each time interval can start as soon as the previous interval’s results are available, enabling parallel computation of the fine solvers which drastically reduces latency. The blue arrows represent the 1-step coarse solves. This pipelining results in a significant speedup over the non-pipelined version.
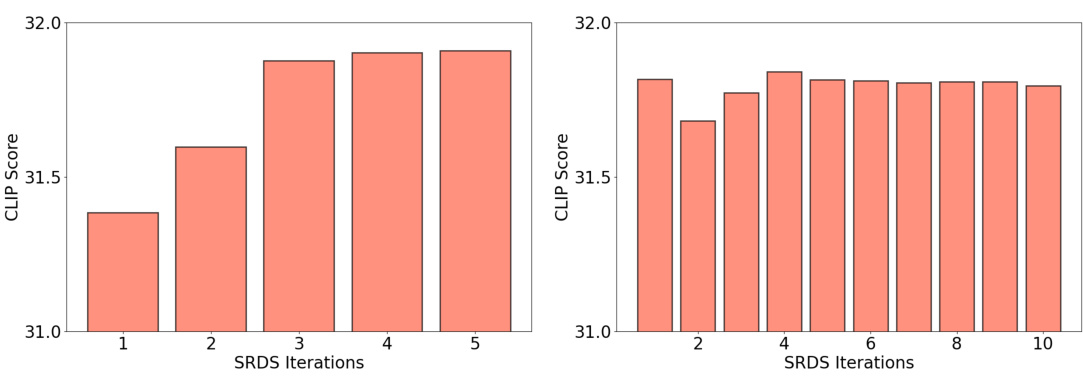
This figure shows the convergence of the Self-Refining Diffusion Sampler (SRDS) algorithm for different trajectory lengths (25 and 100). The y-axis represents the CLIP score, a metric for image quality, and the x-axis shows the number of SRDS iterations. The figure demonstrates that even with a limited number of iterations, SRDS can achieve similar image quality to a full sequential sampling process. Notably, longer trajectories seem to converge faster, highlighting the benefit of parallelism in SRDS.

This figure demonstrates the results of using the Self-Refining Diffusion Sampler (SRDS) algorithm on Stable Diffusion v2. The top row shows images generated by SRDS after only a few iterations, while the bottom row shows the corresponding images generated by a standard, sequential approach. The near-identical quality of the images in both rows highlights that SRDS achieves the same level of accuracy as the sequential method, but much faster, due to its parallelization capabilities.

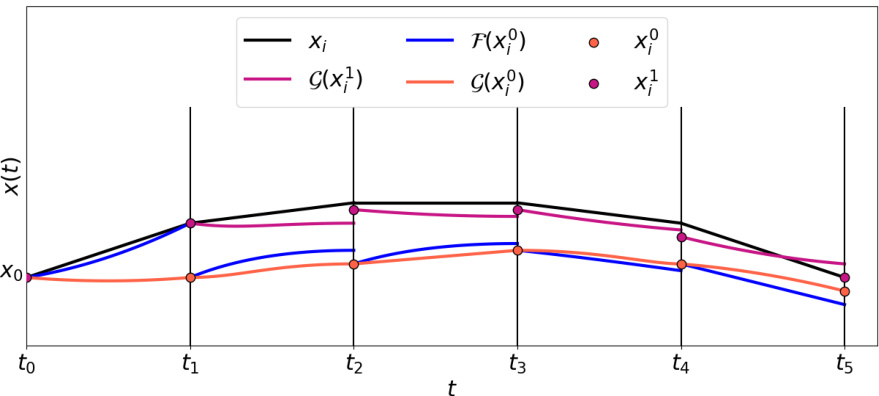
The figure shows how the FID score of generated samples changes as the number of SRDS iterations increases. It demonstrates the rapid convergence of the FID score towards the value obtained by a sequential sampling method within a small number of SRDS iterations. This illustrates the algorithm’s efficiency in achieving high-quality sample generation with fewer steps.

This figure shows sample generations from Stable Diffusion v2 using both the standard method and the SRDS method. The top row displays images generated by SRDS, showing how a relatively quick, rough estimate is iteratively refined to match the quality of the bottom row, which shows images generated using the standard, slower method. The close similarity highlights SRDS’s ability to achieve high-quality results efficiently.

This figure shows the iterative refinement process of the Self-Refining Diffusion Samplers (SRDS) algorithm. Starting from a coarse estimate of the sample (leftmost image), the algorithm iteratively refines the sample through parallel iterations, quickly converging to a high-fidelity sample (rightmost image) that is nearly identical to the final output after just three iterations. This demonstrates the efficiency and effectiveness of the SRDS algorithm in accelerating the sampling process.

This figure shows sample generations from Stable Diffusion v2 using different prompts from the Drawbench dataset. The top row shows the results obtained using the Self-Refining Diffusion Sampler (SRDS) algorithm, and the bottom row displays the results of the serial trajectory (traditional method). The image pairs demonstrate that SRDS produces samples of comparable quality to the traditional approach, but using a significantly faster method. This highlights the algorithm’s efficiency and approximation-free nature.
More on tables

This table presents the results of experiments comparing the performance of the Self-Refining Diffusion Samplers (SRDS) algorithm against a standard Stable Diffusion model (DDIM) using the CLIP score as the evaluation metric. The experiments were performed on the COCO2017 captions dataset with classifier guidance (w=7.5) and evaluated using ViT-g-14. The table shows the number of model evaluations, the CLIP score, and the time per sample for both the standard DDIM approach and SRDS with varying numbers of iterations. Importantly, it highlights the speedup achieved by SRDS due to its early convergence, even without pipeline parallelism.
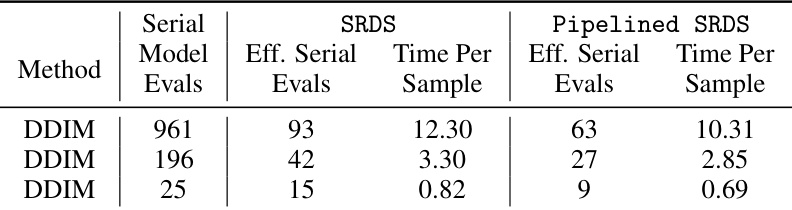
This table compares the performance of three different sampling methods: a sequential DDIM solver, the proposed SRDS method, and a pipelined version of SRDS. The table shows the number of model evaluations performed for each method across three different numbers of denoising steps (25, 196, and 961). The ‘Eff. Serial Evals’ column indicates the effective number of serial model evaluations required for each method, taking into account the parallelization offered by SRDS. The ‘Time Per Sample’ column shows the time (in seconds) taken to generate a single sample using each method. The table highlights that the pipelined version of SRDS offers further improvements in speed over the standard SRDS method, particularly for longer sequences (961 denoising steps).

This table compares the wall-clock speedups achieved by the pipelined version of the Self-Refining Diffusion Sampler (SRDS) and ParaDiGMs, relative to serial Stable Diffusion image generation. The comparison is done across three different numbers of denoising steps (961, 196, and 25) and three different convergence thresholds for ParaDiGMs (1e-3, 1e-2, and 1e-1). The results show that SRDS consistently outperforms ParaDiGMs in terms of speedup, especially when fewer denoising steps are used.

This table compares the performance of SRDS using different sampling algorithms (DDPM, DPM Solver, DDIM) with different numbers of denoising steps (196 and 25). It shows the effective serial evaluations, time per sample, and speedup achieved by SRDS compared to sequential sampling for each combination of solver and number of steps. The results demonstrate SRDS’s ability to significantly accelerate sampling across various methods while maintaining sample quality.

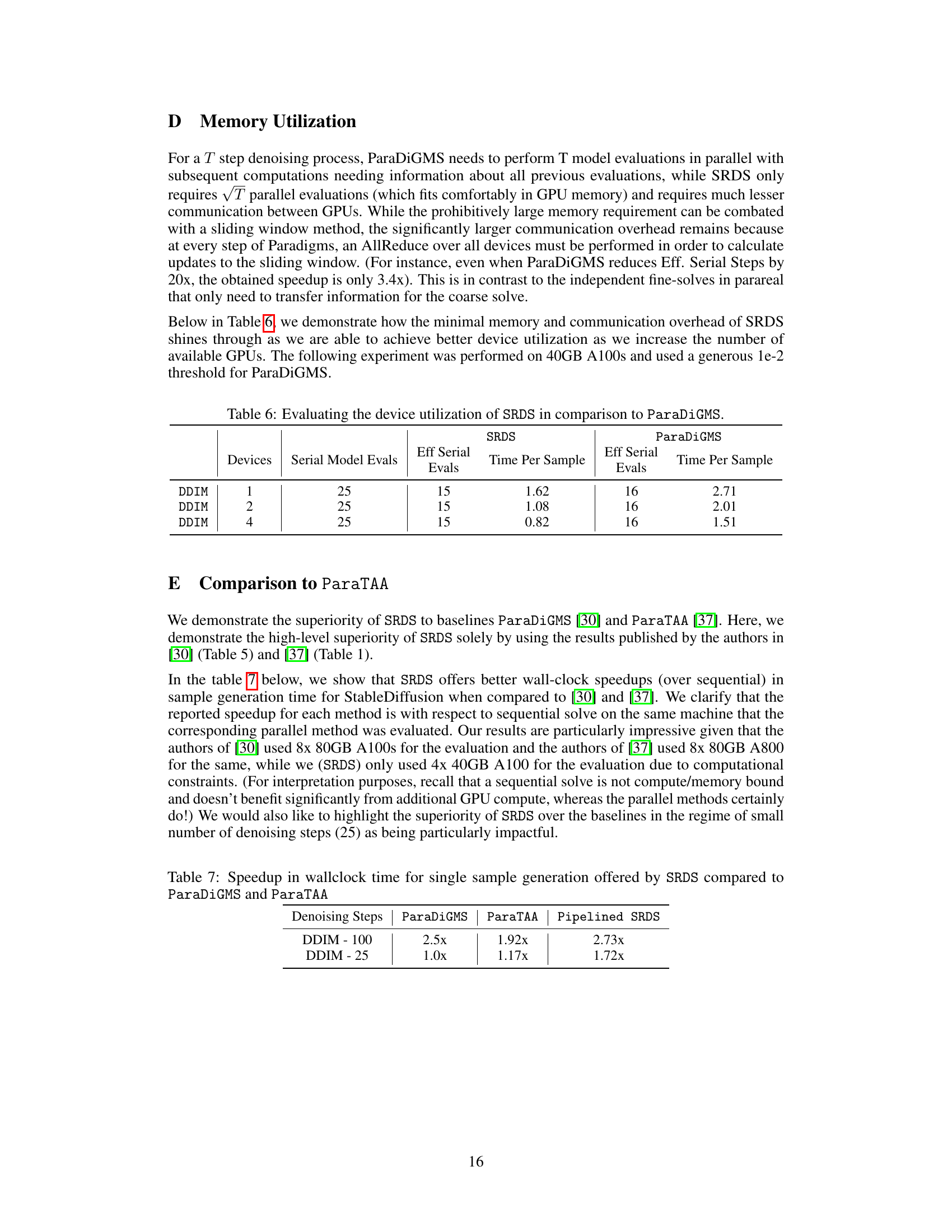
This table compares the device utilization of SRDS and ParaDiGMs for different numbers of GPUs. It shows the effective serial model evaluations and time per sample for both methods, demonstrating that SRDS achieves better device utilization as the number of GPUs increases.

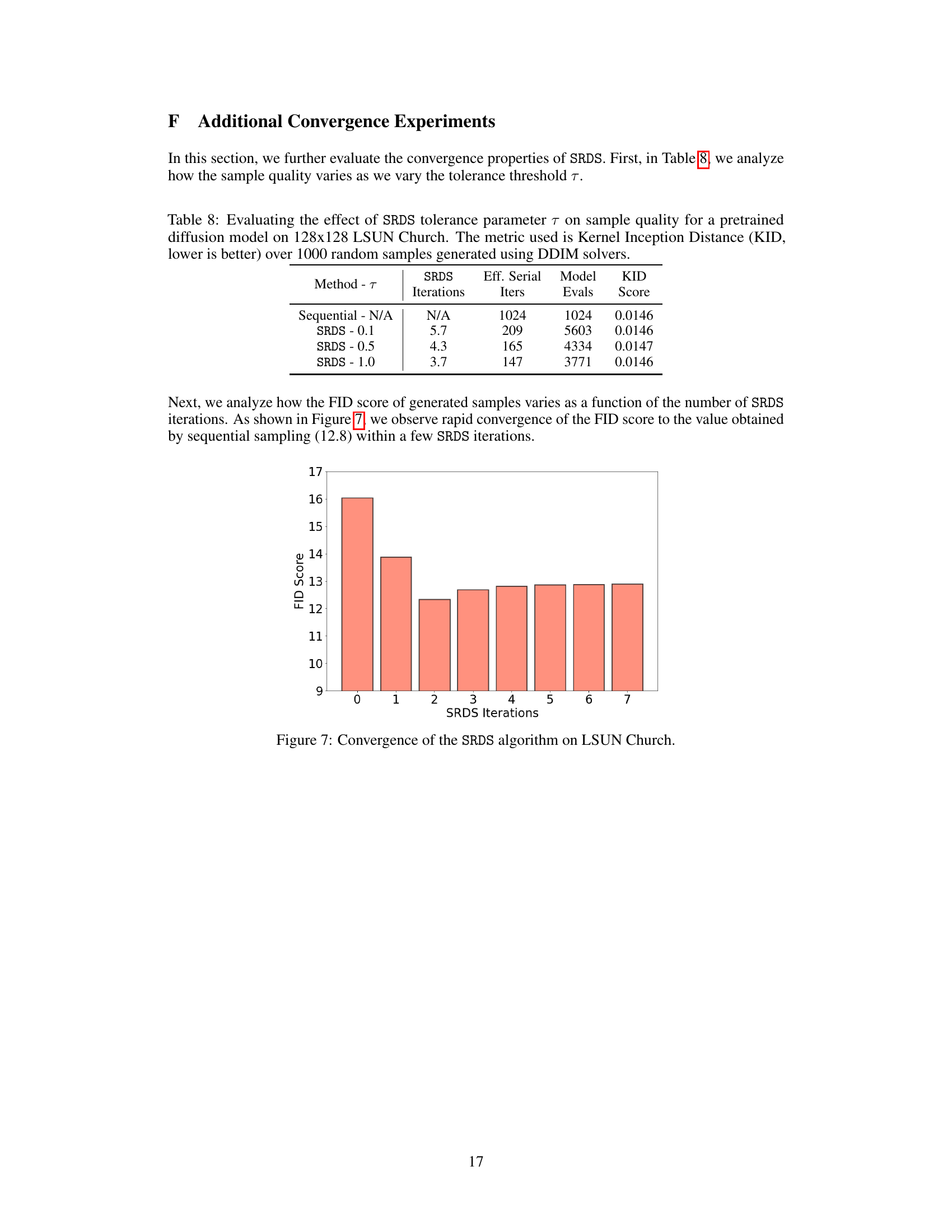
This table compares the wall-clock speedup achieved by Pipelined SRDS, ParaDiGMS, and ParaTAA for generating a single Stable Diffusion sample. The speedup is relative to a sequential sampling method and is shown for both 100 and 25 denoising steps using DDIM. It highlights SRDS’s superior performance, especially with a higher number of denoising steps.
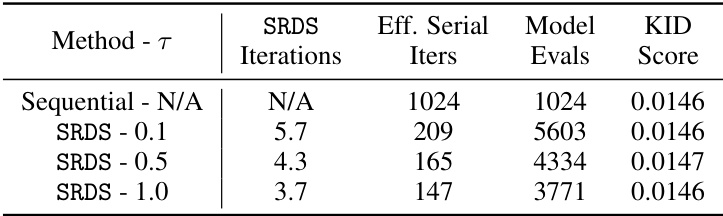
This table presents the FID (Fréchet Inception Distance) scores for the SRDS model and a sequential model as a baseline on four datasets: LSUN Church, LSUN Bedroom, Imagenet, and CIFAR. Lower FID scores indicate better image quality. The table also shows the number of SRDS iterations, effective serial model evaluations (considering parallel evaluations as one), and total model evaluations needed to achieve the reported FID score for each dataset.
Full paper#