↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Sampling from high-dimensional log-concave distributions within complex convex bodies is a fundamental challenge in various fields. Existing Dikin walk algorithms often struggle with high computational costs, especially when dealing with intricate geometries or a large number of constraints. This problem limits their scalability and applicability in large-scale applications.
This research proposes a novel sampling framework using a unified Dikin walk and spectral approximations to address the computational challenges. The approach involves spectral approximations of barrier function Hessians, significantly speeding up each iteration. The researchers proved that their method achieves faster mixing times for both polytopes and spectrahedra compared to existing state-of-the-art algorithms, while maintaining accuracy. This improvement extends the applicability of Dikin walk methods to broader real-world scenarios.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers working on log-concave sampling and optimization. It presents faster algorithms with reduced computational costs, opening avenues for advancements in various applications, including differentially private learning and online convex optimization.
Visual Insights#
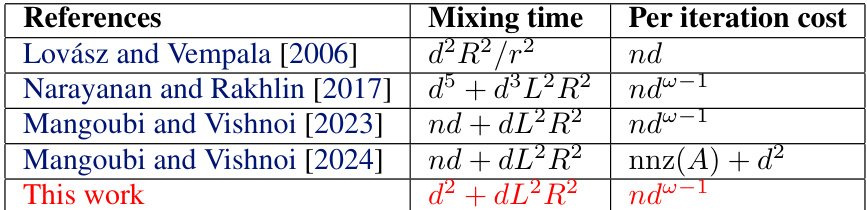
The table compares different algorithms for sampling from a log-concave density over a d-dimensional polytope with n constraints, focusing on the mixing time and per-iteration cost. It highlights the improvement achieved by the authors’ proposed algorithm (This work) compared to existing methods, particularly in terms of faster mixing time, especially when the Lipschitz constant L and the inscribed ball radius r are small. The table assumes that evaluating the function f takes unit time.
In-depth insights#
Logconcave Sampling#
Logconcave sampling is a crucial problem in computational statistics and machine learning, focusing on efficiently generating random samples from a probability distribution that has a log-concave density function. This is a challenging task because log-concave distributions can be complex and high-dimensional. The efficiency of sampling algorithms is often measured by their mixing time, which represents the number of steps required to reach a distribution close to the target distribution. Existing methods often rely on Markov Chain Monte Carlo (MCMC) techniques, but these can be slow, particularly in high dimensions. The paper explores the use of Dikin walks, a type of MCMC method that uses second-order information (Hessian) of a barrier function to propose more informed steps and accelerate convergence. The development of robust and unified Dikin walks is highlighted, capable of handling various convex bodies and log-concave distributions. The paper also focuses on reducing computational costs by using techniques like spectral approximations of Hessians, improving efficiency in high-dimensional settings. The theoretical results presented in the paper analyze the mixing time and computational complexity of the proposed algorithms. Improvements in mixing time and per-iteration costs are compared to existing state-of-the-art methods.
Dikin Walk Variants#
The concept of “Dikin Walk Variants” in the context of a research paper likely explores modifications and extensions of the standard Dikin walk algorithm, a method used for sampling from high-dimensional convex bodies. A core aspect would be examining different strategies for choosing the step size and direction within the walk, potentially using techniques like soft-thresholding or adaptive step size control to improve convergence rates and robustness. The paper might investigate variations in the choice of the underlying barrier function, such as considering universal barriers, or specialized ones for particular problem structures, and comparing their effectiveness. Hessian approximation is another key area of potential variation: different approximation methods (e.g., sketching techniques) may impact computational efficiency versus accuracy. Finally, the analysis of these variants would likely include discussions of their convergence rates and computational complexity, comparing their performance to the original Dikin walk and other sampling methods. The ultimate goal of exploring these variants is likely to achieve faster mixing times and improved sampling efficiency for log-concave distributions within high-dimensional convex bodies.
Hessian Approximation#
Approximating the Hessian matrix is crucial for efficient optimization and sampling algorithms, especially when dealing with high-dimensional data where exact computation is computationally prohibitive. The paper likely explores various approximation techniques, possibly leveraging randomized sketching methods or low-rank approximations to reduce computational costs while maintaining sufficient accuracy. The choice of approximation method would be heavily influenced by the specific structure of the Hessian (e.g., sparsity, low-rank properties). The accuracy of the approximation is a critical factor; insufficient accuracy may lead to slow convergence or incorrect results, while excessive accuracy may negate the computational gains of the approximation. A key part of the analysis likely involves demonstrating bounds on the error introduced by the approximation and how this error affects the overall performance of the algorithm. The authors likely discuss the trade-off between computational efficiency and accuracy, presenting theoretical guarantees for the chosen approximation strategy. This might include bounding the approximation error in terms of spectral norm or Frobenius norm. Ultimately, the success of Hessian approximation hinges on finding a balance between accuracy sufficient for the algorithm’s convergence and speed-ups substantial enough to justify the use of approximation.
Mixing Time Analysis#
A rigorous mixing time analysis is crucial for Markov Chain Monte Carlo (MCMC) methods, as it provides a theoretical guarantee on the number of steps required to obtain samples from the target distribution. The analysis often involves bounding the spectral gap of the transition kernel, which is related to the second largest eigenvalue. Techniques used might include coupling arguments, conductance bounds, or comparison with known chains. The complexity of the analysis depends heavily on the characteristics of the target distribution (e.g., log-concavity, smoothness) and the geometry of the state space (e.g., convexity, dimension). For high-dimensional spaces, obtaining tight bounds can be challenging, often requiring sophisticated mathematical tools and careful analysis. The resulting mixing time bounds frequently depend on parameters of the problem, such as Lipschitz constants, and the warm-start distribution, providing valuable insights into the algorithm’s efficiency and scalability. Analyzing the cost per iteration is also important, as it complements the mixing time to provide a complete picture of the overall computational cost.
Future Research#
Future research directions stemming from this log-concave sampling work could explore several avenues. Improving the dependence on the radius R of the bounding ball for the convex body is a significant area for improvement. The current mixing times have a dependence on R, and eliminating or reducing this dependence would enhance the algorithm’s applicability to a wider range of problems. Investigating alternative barrier functions beyond log-barriers and Lee-Sidford barriers is another promising direction. The paper’s results are largely dependent on the properties of these barriers, and exploring others might unlock better performance or wider applicability. Developing more efficient Hessian approximation techniques is crucial given the computational costs of dealing with high-dimensional problems. The paper employs sketching, but there’s potential to explore alternative, potentially faster, approximation methods. Lastly, extending the approach to non-log-concave distributions while maintaining efficient mixing and per-iteration complexity would be a significant contribution. This would broaden the applicability of the methods and address a much wider class of problems.
More visual insights#
More on tables
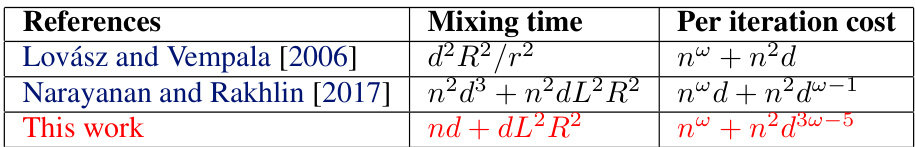
This table compares different algorithms for sampling from a log-concave density over a d-dimensional polytope with n constraints. The algorithms are compared based on their mixing time and per-iteration cost. The table highlights that the proposed algorithm in this paper achieves the fastest mixing time among the Dikin walk algorithms, outperforming even the hit-and-run method under certain conditions.

This table compares different algorithms for sampling from log-concave distributions over polytopes. It shows the mixing time and per-iteration cost for each algorithm. The algorithms compared are Lovász and Vempala (2006), Narayanan and Rakhlin (2017), Mangoubi and Vishnoi (2023), Mangoubi and Vishnoi (2024), and the proposed algorithm in this paper. The table highlights that the proposed algorithm achieves the fastest mixing time among all Dikin walk algorithms, and outperforms hit-and-run in certain scenarios.
Full paper#



















