↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Managing and storing cluster assignments for massive datasets, like those in vector similarity search databases, is computationally expensive and consumes significant storage. Existing methods often use artificial labels or rely on lossy compression, leading to suboptimal performance. This creates a critical need for efficient, lossless techniques that can handle the scale and complexity of modern datasets without compromising accuracy.
This research introduces Random Cycle Coding (RCC), a novel, theoretically optimal method that addresses these issues. RCC cleverly encodes cluster assignments using cycles within a permutation of the data elements, thereby implicitly representing the clusters. The method requires no training data, has quasi-linear time complexity, and consistently outperforms existing methods in terms of storage efficiency and computational cost. This approach is demonstrated to yield substantial space savings (up to 70%) in vector databases for similarity search applications.
Key Takeaways#
Why does it matter?#
This paper is highly important for researchers working with large-scale datasets, particularly in areas like vector databases and similarity search. Its optimal compression method offers significant storage and bandwidth savings, directly addressing the challenges of handling ever-growing datasets. The quasi-linear time complexity makes it scalable for practical applications, and the theoretical optimality provides a strong foundation for future work in lossless data compression. Moreover, the elimination of artificial labels simplifies data management and opens new avenues for improving the efficiency of existing systems.
Visual Insights#
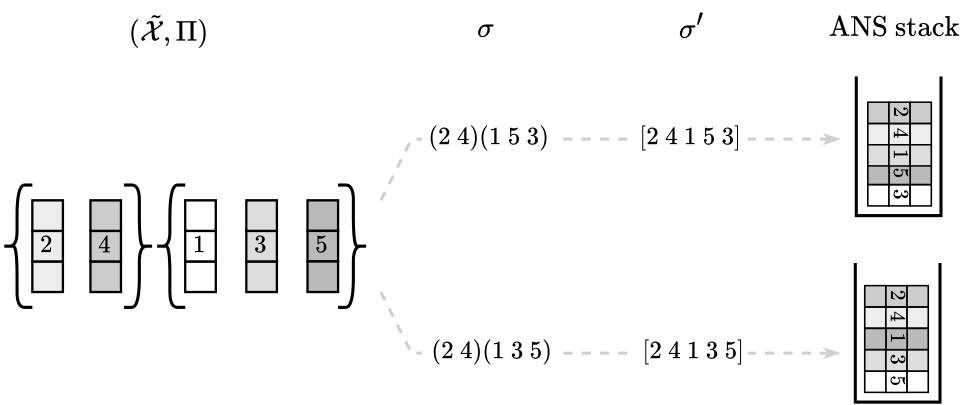
This figure illustrates the Random Cycle Coding (RCC) method. It shows how cluster assignments are encoded as cycles within a permutation. The left side shows the initial data and cluster assignments. The middle shows how a permutation is created from the relative order of the elements and then transformed using Foata’s Bijection. This permutation represents the cluster assignments. The right shows how the final permutation is encoded in an ANS (Asymmetric Numeral Systems) stack for efficient storage.
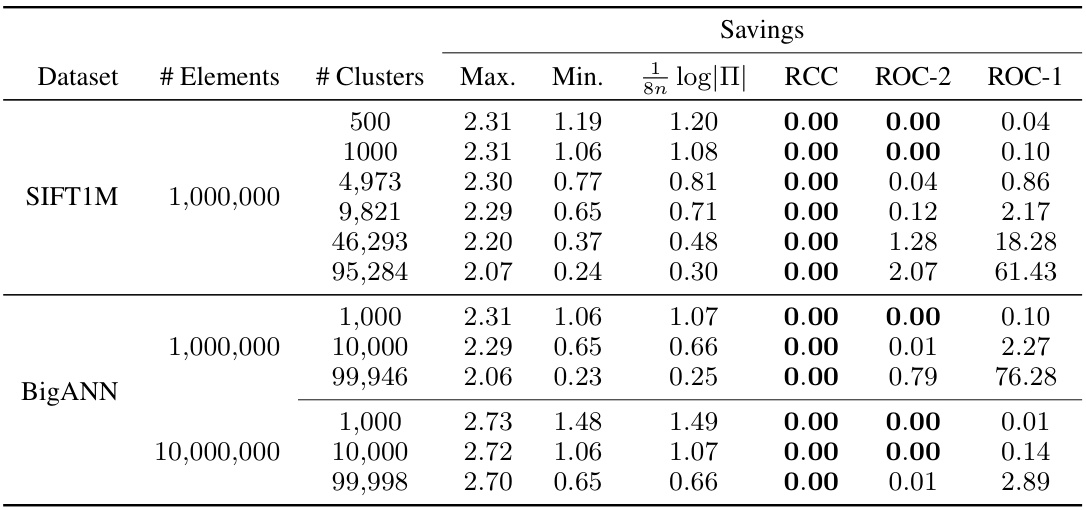
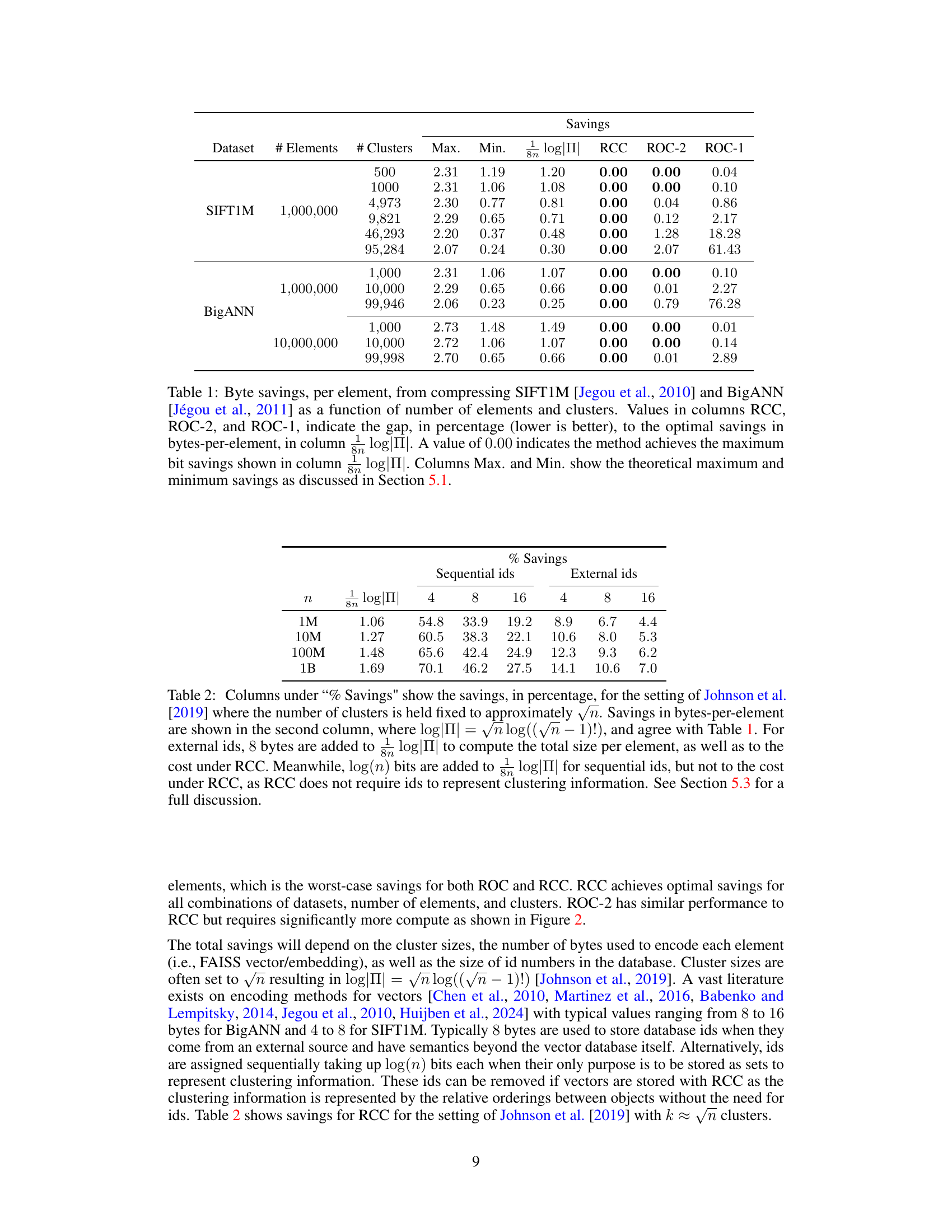
This table presents the byte savings achieved by three different methods (RCC, ROC-2, and ROC-1) when compressing two large-scale datasets, SIFT1M and BigANN, with varying numbers of elements and clusters. The savings are compared to the theoretical optimal savings (log|Π|). Lower values indicate better performance, with 0.00 representing optimal compression.
In-depth insights#
RCC: Optimal Coding#
The heading ‘RCC: Optimal Coding’ suggests a focus on the optimality of a Random Cycle Coding (RCC) method. This likely involves demonstrating that RCC achieves the theoretical Shannon limit for lossless compression of cluster assignments. The optimality claim would need to be rigorously proven, potentially by showing that RCC’s compression rate matches the entropy of the cluster assignment information. A key aspect would be showing how RCC achieves this optimality without relying on any training data or machine learning, making it a truly universal and efficient solution. The discussion should delve into the algorithm’s core mechanics and complexities, analyzing its efficiency relative to other encoding schemes, and exploring its scalability for large datasets. A crucial point of interest would be the relationship between cluster size, data size, and RCC’s performance. A successful demonstration of optimality would likely involve mathematical proofs, detailed algorithmic descriptions, and empirical validation using large-scale datasets. The section should conclude by highlighting the practical significance of RCC’s optimality, illustrating its effectiveness in scenarios like vector database management, where efficient cluster representation is vital.
Bits-Back Encoding#
Bits-back coding is a powerful entropy coding method particularly well-suited for latent variable models. Its key advantage lies in its ability to achieve a bit rate equal to the cross-entropy, even without direct access to the marginal distribution of the observed variable. This is accomplished by cleverly using an invertible sampling process with Asymmetric Numeral Systems (ANS), ensuring perfect fidelity upon decoding. The method elegantly interleaves sampling and encoding steps, efficiently leveraging the posterior distribution to reduce the overall bitrate. Crucially, the efficacy of bits-back coding is not contingent on possessing the true data distribution; instead, it relies on the conditional likelihood and the prior distribution of the latent variables. This makes it particularly attractive in scenarios where obtaining the true distribution is computationally expensive or otherwise infeasible. The technique’s ability to bypass the need for the exact marginal distribution is a significant practical advantage, enhancing its applicability across various machine learning tasks and data compression problems.
Vector DB Savings#
The section on ‘Vector DB Savings’ would likely detail the practical application of the proposed Random Cycle Coding (RCC) method within the context of vector databases. It would likely present empirical evidence demonstrating significant storage reductions compared to existing techniques. Key aspects would include quantifiable savings in bytes per element, perhaps showcasing different datasets and varying cluster sizes for a comprehensive analysis. A comparison to other lossless compression methods would be essential, highlighting RCC’s superior performance, potentially in terms of both compression ratio and computational efficiency. The results would likely demonstrate how RCC eliminates the need for explicit vector IDs, further boosting storage savings and improving the overall efficiency of similarity search operations in vector databases. Finally, the discussion might also touch upon the scalability and robustness of RCC across a range of vector database scenarios.
ROC Comparison#
A thoughtful analysis of a hypothetical ‘ROC Comparison’ section in a research paper would necessitate a deep dive into the specifics of the compared methods. It’s crucial to understand what type of ROC curves are being compared, precision-recall curves versus receiver operating characteristic curves, as this dictates the metrics used. A robust comparison requires more than just visual inspection; it should quantify differences using statistical measures. Are the p-values for comparing AUCs reported? Are confidence intervals presented to illustrate uncertainty in the estimations? The comparison must also account for the experimental setup. Were the datasets and parameters consistent across all methods? Any discrepancies could skew the results, making conclusions unreliable. Furthermore, the discussion should go beyond simple numerical comparisons to interpret the results in the context of the broader application domain. What do the differences mean for practical usage? A truly comprehensive analysis would also address computational aspects. How does the runtime and memory usage compare across methods? This could be crucial for choosing the most practical approach. Finally, a compelling comparison would discuss limitations of each method. What are the strengths and weaknesses, and how do these relate to the application at hand?
Future Extensions#
Future research directions stemming from this work on Random Cycle Coding (RCC) for lossless cluster assignment compression could explore several avenues. Extending RCC to handle non-uniform cluster sizes more effectively is crucial, as real-world data often deviates from uniform distributions. Investigating the impact of different data types and embedding methods on RCC’s performance is essential for broader applicability. Developing faster encoding and decoding algorithms while maintaining optimality is another key area, particularly for extremely large datasets. Finally, adapting RCC to dynamic scenarios where clusters evolve over time would enhance its practical value in applications like evolving vector databases or online clustering systems. These extensions would significantly increase the practical utility of RCC.
More visual insights#
More on figures
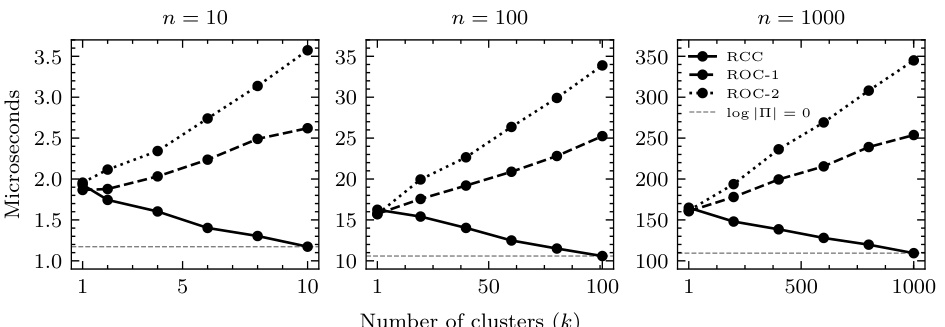
The figure shows the median encoding and decoding times for three different methods: RCC, ROC-1, and ROC-2. The x-axis represents the number of clusters (k), while the y-axis represents the time in microseconds. There are three separate graphs, one each for 10, 100, and 1000 elements (n). The dashed line represents the theoretical minimum time, where log|Π| = 0. The figure demonstrates the computational efficiency of RCC, especially as the number of elements increases.
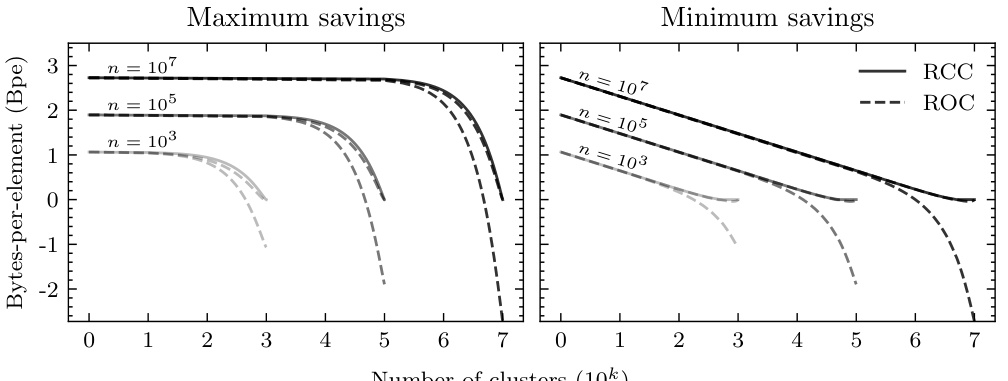
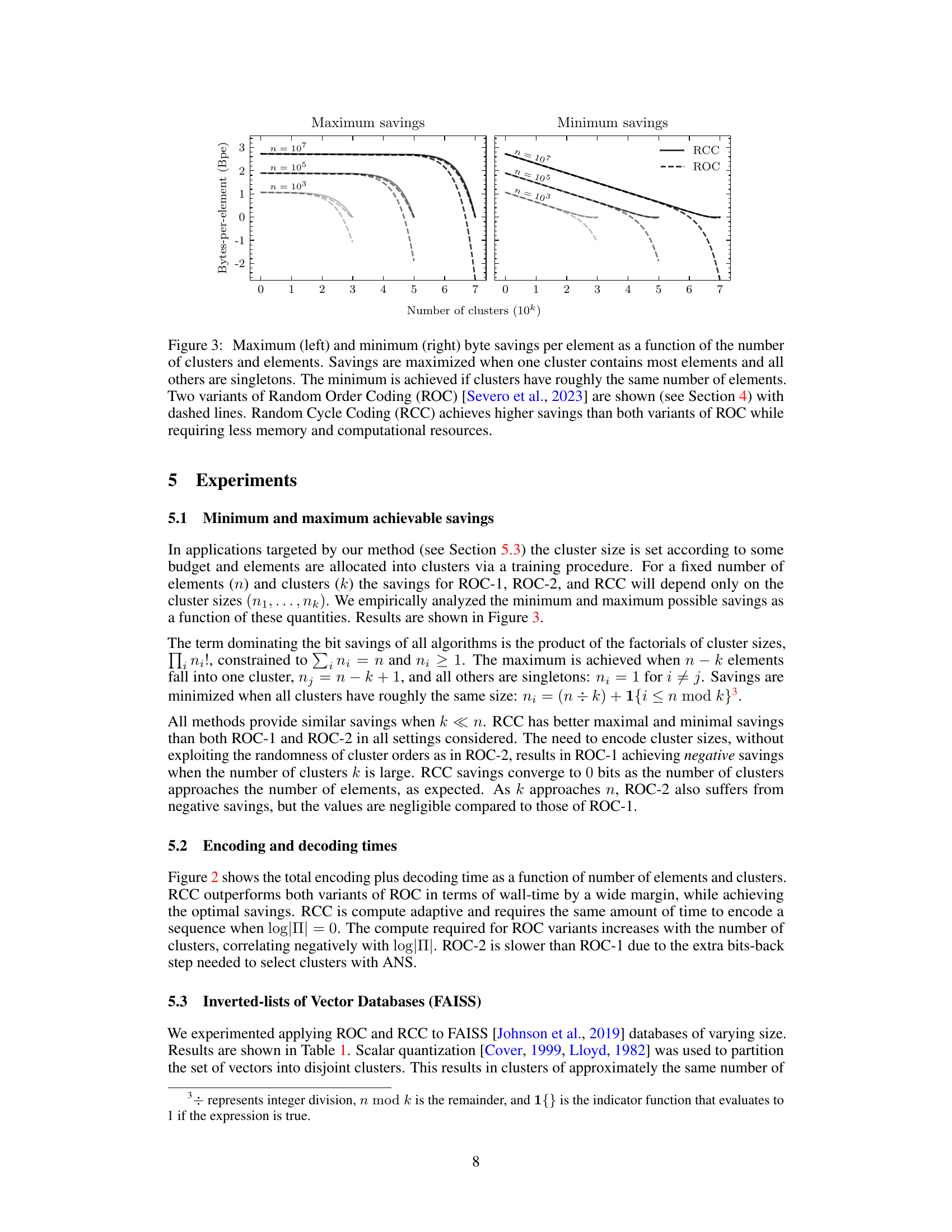
This figure shows the maximum and minimum byte savings per element achieved by Random Cycle Coding (RCC) and two variants of Random Order Coding (ROC) as a function of the number of clusters and the number of elements. The x-axis represents the number of clusters (in thousands), and the y-axis shows the bytes-per-element savings. Different curves represent different numbers of total elements (10³, 10⁵, and 10⁷). The maximum savings occur when one cluster is significantly larger than the others, and the minimum savings occur when clusters are of similar size. The figure demonstrates that RCC consistently outperforms ROC in terms of savings.

The figure displays the median time taken for encoding and decoding across 100 runs using two different methods: Random Cycle Coding (RCC) and Random Order Coding (ROC). The number of elements (n) and clusters (k) are varied across three subplots, showing the median time increases quasi-linearly with the number of clusters and scales with the number of elements. The graph highlights RCC’s superior performance in terms of speed compared to ROC.
Full paper#