↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Training massive neural networks efficiently while maintaining desirable structures (e.g., sparsity) is a major challenge in deep learning. Existing methods struggle to guarantee both convergence and the desired structure simultaneously. Adaptive methods, while empirically successful, lack theoretical guarantees on structure.
This paper introduces RAMDA, a Regularized Adaptive Momentum Dual Averaging algorithm that overcomes these limitations. RAMDA incorporates a novel inexactness condition and an efficient subproblem solver, ensuring convergence while attaining the ideal structure induced by the regularizer. Experiments show RAMDA’s superiority over existing adaptive methods in computer vision, language modeling, and speech recognition tasks, demonstrating its effectiveness in large-scale modern applications.
Key Takeaways#
Why does it matter?#
This paper is crucial because it addresses the challenge of training large structured neural networks efficiently and effectively. Its introduction of RAMDA, a novel algorithm with structure guarantees, offers a significant advancement over existing methods. This is particularly important given the increasing trend towards larger and more complex models in various fields. The research opens new avenues for developing more efficient and effective training algorithms for structured neural networks, improving the performance and scalability of deep learning models.
Visual Insights#

This figure visualizes the training process of various models, illustrating the relationship between the weighted structured sparsity and validation performance (accuracy or perplexity, depending on the specific model) over epochs. Each subplot represents a different experiment, such as ResNet50 on ImageNet, Transformer-XL on WikiText-103, and others. The plots demonstrate how the weighted structured sparsity evolves during the training process and how it relates to the validation performance, helping to evaluate the effectiveness of the RAMDA algorithm compared to other methods. The figure also shows the number of batches processed in each step for the Transformer-XL model.
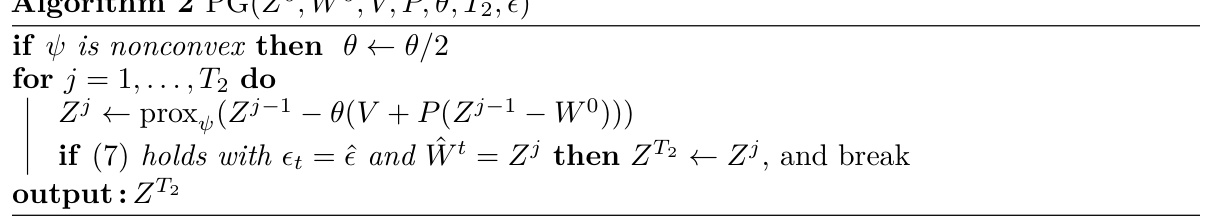
This table presents the weighted group sparsity and validation accuracy achieved by different algorithms (ProxGen and RAMDA) using two different subproblem stopping criteria: no early stopping and early stopping. The results are shown for two different models (VGG19 and ResNet50) and two different datasets (CIFAR10 and CIFAR100). The table demonstrates the impact of the subproblem solver’s stopping criterion on the final model’s performance in terms of accuracy and sparsity.
In-depth insights#
RAMDA Algorithm#
The RAMDA algorithm, a novel approach for training structured neural networks, stands out with its regularized adaptive momentum dual averaging mechanism. Unlike previous methods, RAMDA provides guarantees for both convergence and structure identification, addressing a key limitation in existing regularized adaptive methods. This is achieved through a carefully designed inexactness condition for the subproblem solver, ensuring computational efficiency without sacrificing theoretical guarantees. The algorithm cleverly leverages manifold identification theory to show that iterates attain the ideal structure induced by the regularizer at the stationary point, ensuring locally optimal structure. The use of a diagonal preconditioner provides adaptiveness, making it suitable for modern large-scale architectures like transformers. Empirical results demonstrate RAMDA’s consistent outperformance in various tasks, showcasing its efficiency and effectiveness in obtaining models that are both predictive and structurally optimal.
Inexact Subproblem#
The core challenge addressed in the research paper revolves around efficiently solving complex subproblems encountered during the training of structured neural networks. These subproblems, arising from the inclusion of nonsmooth regularizers and diagonal preconditioners, lack closed-form solutions, demanding iterative approximation methods. The paper’s significant contribution lies in the careful design of an inexactness condition, ensuring convergence guarantees despite the approximate solutions. This condition, combined with a companion efficient solver (a proximal gradient method), allows the algorithm to make progress even when an exact solution to the subproblem is computationally infeasible. This focus on inexact subproblem solving is crucial for scaling the methodology to handle the large-scale problems common in modern deep learning, particularly those involving structured sparsity. The innovative inexactness condition and efficient solver are key factors enabling the proposed RAMDA algorithm to achieve both outstanding predictive performance and the desired optimal structural properties in the final neural network model.
Structure Guarantees#
The core of this research lies in achieving structure guarantees during the training of structured neural networks. Existing methods often converge to a point possessing the desired structure, but the iterates themselves may not reflect this structure until asymptotically. This work uniquely addresses this by establishing that, after a finite number of iterations, the algorithm’s iterates attain the ideal structure induced by the regularizer at the asymptotic convergence point. This is a significant leap, guaranteeing that the learned model not only converges to a desired structure but explicitly exhibits it during the training process. Manifold identification theory is leveraged to formally prove this property. The resulting advantage is the creation of models that are not only effective but possess the locally optimal structure defined by the regularizer, a major advancement over existing adaptive methods which lack such precise structural control. This is further enhanced by an efficient inexact subproblem solver, making the approach practical for real-world large-scale neural networks.
Empirical Results#
The empirical results section of a research paper is crucial for validating the claims and hypotheses presented earlier. A strong empirical results section will present findings clearly and concisely, using appropriate visualizations such as tables and graphs. It should also include a discussion of the limitations of the experiments and potential sources of error. Statistical significance is paramount, and the methods used to assess it (e.g., p-values, confidence intervals) should be explicitly stated. A comprehensive empirical results section might also include ablation studies, showcasing the effect of removing individual components, and comparison against prior state-of-the-art methods, demonstrating improvement. Robustness checks, such as varying hyperparameters, and analyses exploring the impact of different datasets, are vital to confirm the generalizability of findings. Ultimately, a well-written empirical results section provides strong evidence supporting the study’s central arguments while acknowledging limitations, fostering trust and credibility in the research.
Future Work#
Future research directions stemming from this RAMDA algorithm could explore several promising avenues. Extending RAMDA’s theoretical guarantees to non-convex settings is crucial, given the prevalence of non-convex objective functions in deep learning. A deeper investigation into optimal choices for the step size and momentum parameters across various architectures and datasets would further enhance RAMDA’s practical applicability. Incorporating more sophisticated preconditioners beyond the diagonal approximation used here could potentially yield even faster convergence and improved structure identification. Exploring different regularization techniques, such as those promoting other desired structural properties beyond sparsity, would broaden RAMDA’s usefulness for different types of neural networks. Finally, a comprehensive empirical evaluation across a wider array of tasks and datasets is warranted to fully assess RAMDA’s robustness and comparative advantages.
More visual insights#
More on figures
This figure displays the trends of weighted structured sparsity and validation metrics (accuracy, perplexity, or loss) across various epochs for multiple algorithms and datasets. The algorithms are compared on different neural network architectures for image classification (ResNet50 on ImageNet, VGG19 on CIFAR10, ResNet50 on CIFAR10), language modeling (Transformer-XL on WikiText-103), and speech synthesis (Tacotron2 on LJSpeech). The plot for Transformer-XL shows a different scale because one step in this model processes 10 batches of data, resulting in 8401 batches per epoch.

This figure shows the training performance of different algorithms over epochs for various tasks. The plots show the weighted structured sparsity and validation metrics (accuracy, perplexity, or loss) for each algorithm. The x-axis represents the training epochs, while the y-axis represents the weighted structured sparsity and validation metrics. The figure highlights how RAMDA maintains a high level of structured sparsity while achieving competitive validation performance. Note that the scale of the x-axis differs for each subplot, and for Transformer-XL, one step represents processing 10 batches (each with batch size of 64), so one epoch contains 8401 steps.

This figure shows the group sparsity level and validation performance (accuracy or perplexity or loss) over epochs for various models and datasets. It compares the performance of RAMDA with other methods, highlighting the stability of RAMDA’s sparsity level and its competitive performance. The different subplots represent results from various experimental settings, including different network architectures (ResNet50, Transformer-XL, Tacotron2), datasets (ImageNet, WikiText-103, LJSpeech, MNIST, CIFAR10, CIFAR100), and regularization techniques.

This figure displays the weighted group sparsity and validation accuracy/perplexity/loss for several methods (ProxSGD, ProxSSI, ProxGen, RMDA, RAMDA) across different datasets and model architectures. Each plot shows how these metrics evolve over the training epochs. The Transformer-XL plot uses a different step size than the other plots. The plots show how the performance and sparsity of various methods converge over time and indicate the relative effectiveness of each algorithm.

This figure shows the change in weighted group sparsity and validation performance (accuracy or perplexity) for various algorithms (ProxSGD, ProxSSI, ProxGen, RMDA, and RAMDA) across different datasets and model architectures over the training epochs. The plot highlights the stability of RAMDA’s sparsity level in comparison to other methods, particularly towards the end of training. The difference in x-axis scales across subplots is because of varying batch sizes and epoch lengths used for training different models.

The figure shows the weighted group sparsity level at the last epochs for different algorithms (ProxSGD, ProxSSI, ProxGen, RMDA, and RAMDA) across various experiments: ResNet50 on ImageNet, Transformer-XL on WikiText-103, Tacotron2 on LJSpeech, Logistic Regression on MNIST, VGG19 on CIFAR10, VGG19 on CIFAR100, ResNet50 on CIFAR10, and ResNet50 on CIFAR100. It illustrates the stability of RAMDA’s sparsity level compared to the fluctuations observed in other methods.

This figure shows the change of group sparsity and validation accuracy over epochs for different algorithms on various datasets. The datasets include ImageNet, WikiText-103, LJSpeech, MNIST, and CIFAR10/100. The algorithms compared are MSGD, ProxSGD, ProxSSI, ProxGen, RMDA, and RAMDA. The plots illustrate the performance of each algorithm in terms of achieving structured sparsity and maintaining prediction accuracy. The Transformer-XL plot has a different x-axis scale due to the larger batch size.

The figure shows the weighted structured sparsity for different algorithms (ProxSGD, ProxSSI, ProxGen, RMDA, and RAMDA) over epochs for various experiments: ResNet50 on ImageNet, Transformer-XL on WikiText-103, Tacotron2 on LJSpeech, Logistic Regression on MNIST, VGG19 on CIFAR10, VGG19 on CIFAR100, ResNet50 on CIFAR10, and ResNet50 on CIFAR100. It demonstrates the stability of RAMDA’s sparsity level compared to the fluctuating behavior of other algorithms.
More on tables

This table presents the weighted group sparsity and validation accuracy achieved by ProxGen and RAMDA on CIFAR10 and CIFAR100 datasets under two different subproblem stopping criteria: no early stopping and early stopping. The results show the impact of the early stopping criterion on both the model’s performance and sparsity level.
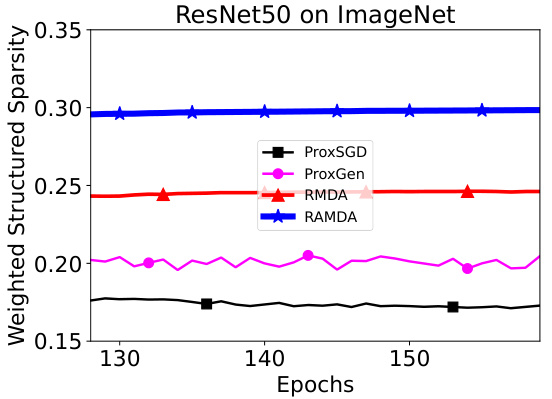
This table compares the performance of ProxSSI and ProxGen on CIFAR10 and CIFAR100 datasets in terms of weighted group sparsity, validation accuracy, and training time per epoch. It highlights the significant difference in training time between the two algorithms, with ProxGen being substantially faster.

This table presents the results of experiments conducted on the ImageNet dataset using the ResNet50 model. It compares the performance of several algorithms, including MSGD, ProxSGD, ProxGen, RMDA, and RAMDA, in terms of both weighted group sparsity (a measure of the model’s structure) and validation accuracy. RAMDA achieves the highest validation accuracy and the highest weighted group sparsity among all algorithms compared.

This table presents the results of training a Transformer-XL language model on the WikiText-103 dataset using different optimization algorithms. The algorithms are compared based on their validation perplexity (a measure of how well the model predicts the next word in a sequence), the level of weighted group sparsity achieved (a measure of the model’s structure), and the training time per epoch. The table shows that RAMDA achieves the lowest perplexity and highest sparsity, suggesting that it is a more efficient and effective method for training structured neural networks for language modeling.
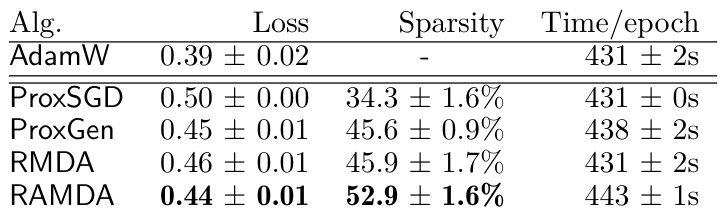
This table presents the results of training the Tacotron2 model for speech synthesis on the LJSpeech dataset using different optimization algorithms. The algorithms compared include AdamW (a baseline without structured sparsity), ProxSGD, ProxGen, RMDA, and RAMDA. The table shows the validation loss achieved by each algorithm, along with the weighted group sparsity level and the training time per epoch. The key metric is validation loss, with lower values indicating better performance. The sparsity metric indicates the degree of structured sparsity achieved in the trained model.

This table summarizes the algorithms used in the paper’s experiments, comparing them based on their unregularized counterpart and the method used to solve their subproblems. It shows that RAMDA leverages MADGRAD for its unregularized counterpart and uses a proximal gradient (PG) method for its subproblem. Other methods such as RMDA, ProxSGD, ProxGen, and ProxSSI are also presented with their respective unregularized counterparts and subproblem solvers.

This table presents the results of comparing various algorithms (ProxSGD, ProxSSI, ProxGen, RMDA, and RAMDA) on image classification tasks using smaller datasets (MNIST, CIFAR10, CIFAR100). The algorithms are evaluated based on their validation accuracy and the level of group sparsity achieved. This allows for a comparison of the algorithms’ performance on both prediction accuracy and the ability to induce a desired structure in the model.

This table presents the results of an experiment comparing several algorithms on a six-layer fully connected neural network trained on the FashionMNIST dataset. The algorithms compared are MSGD, ProxSGD, ProxGen, RMDA, and RAMDA. The table shows the validation accuracy and low-rank level achieved by each algorithm. The low-rank level is a measure of the extent to which each algorithm produces a low-rank model, which is a type of structured sparsity.

This table presents the results of experiments comparing different optimization algorithms on a masked image modeling task using a modified vision transformer and the CIFAR10 dataset. The algorithms compared include AdamW (a baseline without regularization), ProxSGD, ProxGen, RMDA, and the proposed RAMDA. The table shows the validation loss and the achieved low-rank level for each algorithm, demonstrating the effectiveness of RAMDA in achieving a low-rank structure while maintaining competitive prediction performance.
Full paper#



















