↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Causal representation learning (CRL) aims to recover latent causal variables and their relationships from high-dimensional data. While previous studies focused on infinite-sample regimes, this work tackles the more realistic finite-sample setting. Existing CRL methods lack probabilistic guarantees for finite samples, making their reliability questionable in real-world applications where data is limited. This creates a critical need for sample complexity analysis.
This paper addresses this challenge by providing the first sample complexity analysis for interventional CRL. The authors focus on general latent causal models, soft interventions, and linear transformations from latent to observed variables. They develop novel algorithms and establish sample complexity guarantees for both latent graph and variable recovery. The results show that a surprisingly small number of samples is sufficient to achieve high accuracy, offering improved theoretical guarantees and practical guidelines for CRL research.
Key Takeaways#
Why does it matter?#
This paper is crucial because it bridges the gap between theoretical identifiability and practical applications in causal representation learning. By providing the first sample complexity analysis for finite-sample regimes, it offers much-needed practical guidance for researchers, enabling more reliable and efficient CRL algorithms. The explicit dependence on the dimensions of the latent and observable spaces provides valuable insights for designing more scalable and robust CRL methods. Furthermore, the work opens new avenues for further research focusing on non-parametric latent models, different intervention types, and sample-efficient algorithms. This will lead to more practical and reliable causal inference and representation learning systems.
Visual Insights#
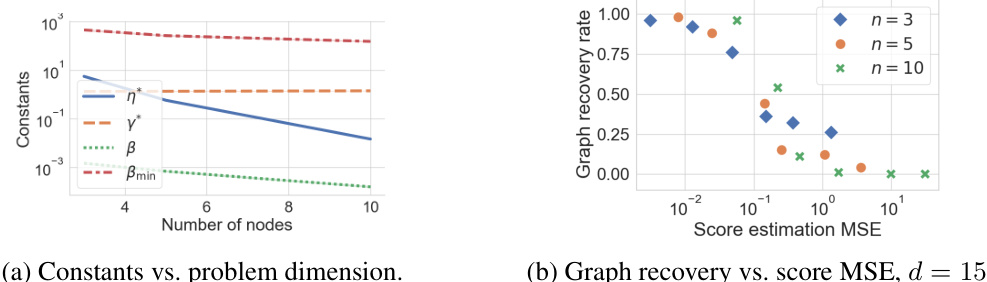
Figure 1 presents numerical evaluations of the theoretical analyses provided in Section 5. (a) shows the variation of model constants (η*, γ*, β, βmin) with respect to the latent dimension n. These constants determine the sample complexity bounds. (b) shows the variation of graph recovery rates with respect to the mean squared error of score estimations. Each data point corresponds to a different sample size N and different latent dimensions n. The graph recovery rate decays linearly with respect to log(MSE) in low MSE regime and it plateaus as the MSE increases. This behavior is due to the sensitivity of the proposed algorithms to the errors in estimating the approximate matrix ranks.

This table presents the sample complexity results for achieving δ-PAC graph recovery using the RKHS-based score estimator. It shows that the error in graph recovery, δG(N), decreases exponentially with the number of samples, N. The expression for δG(N) involves model dependent constants (β, βmin, η*, γ*) and the latent dimension (n).
Full paper#