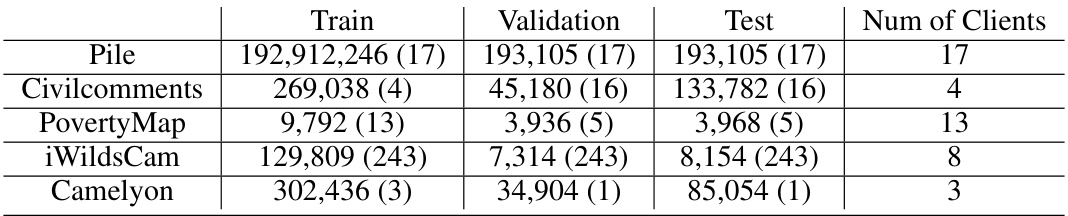
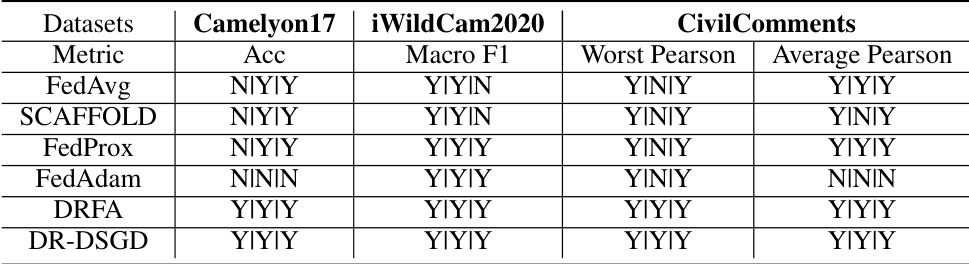
↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Federated learning faces a significant hurdle: the inconsistent data distribution and volume across participating devices. This inconsistency negatively impacts model generalization and creates a need for advanced optimization techniques to maintain performance across diverse data sources. Existing solutions often suffer from high communication overhead and sample complexity, limiting their practical applicability.
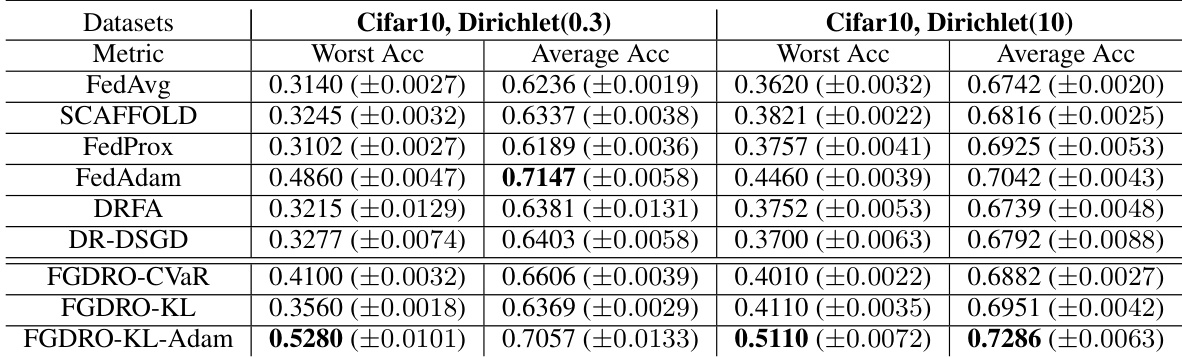
This paper proposes novel, communication-efficient algorithms to optimize Federated Group Distributionally Robust Optimization (FGDRO). The algorithms introduced, FGDRO-CVaR and FGDRO-KL, are tailored for specific regularization techniques (CVaR and KL, respectively), achieving substantial reductions in communication costs compared to existing methods. Furthermore, a new algorithm, FGDRO-KL-Adam, integrates adaptive Adam-type local updates within the FGDRO-KL framework, potentially surpassing the performance of standard SGD-type local steps, all while maintaining a low communication overhead.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in federated learning as it tackles the heterogeneity in data volumes and distributions at different clients, a major challenge affecting model generalization. The proposed communication-efficient algorithms offer significant improvements over existing methods and provide new avenues for research in distributionally robust optimization. It also presents novel techniques for handling non-smooth optimization problems, opening doors for similar advancements in other machine learning domains.
Visual Insights#

This figure shows the ablation studies performed to analyze the impact of communication interval and local Adam steps on the algorithm performance. (a) shows how varying the communication interval affects the training loss for FGDRO-CVaR and FGDRO-KL-Adam on the Camelyon dataset. (b) compares the training loss and testing average log-perplexity for FedAdam and LocalAdam algorithms on the Pile dataset, demonstrating the effectiveness of using Adam-type updates in local steps.

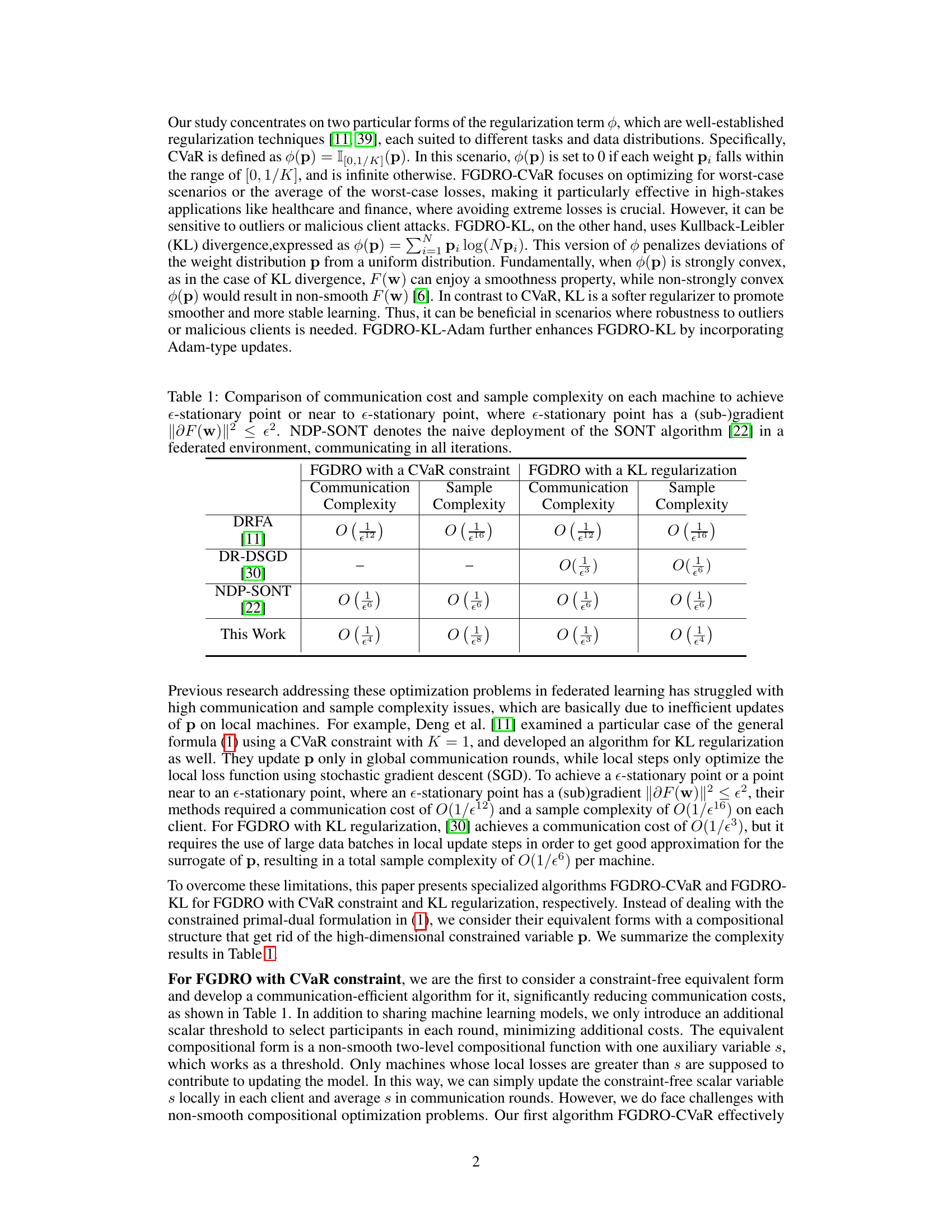
This table compares the communication and sample complexities of several algorithms for solving distributionally robust optimization problems in federated learning. The algorithms are categorized by the type of constraint used (CVaR or KL) and whether they are proposed in prior work or in this paper. The complexities are expressed in terms of the desired precision level (e). The table highlights the improvements in communication and sample complexity achieved by the proposed algorithms in this work.
In-depth insights#
FGDRO-CVaR Algorithm#
The FGDRO-CVaR algorithm tackles the challenge of federated group distributionally robust optimization with a CVaR constraint. Its key innovation lies in reformulating the constrained problem into an equivalent unconstrained two-level compositional optimization problem. This clever reformulation replaces the high-dimensional weight vector with a single scalar threshold variable, significantly reducing complexity. The algorithm leverages moving averages to accurately estimate gradients, enhancing efficiency. Furthermore, it achieves a communication cost of O(1/ε⁴) and a sample complexity of O(1/ε⁸) on each machine. This represents a substantial improvement over existing methods that struggle with high communication and sample complexity. The algorithm’s effectiveness is demonstrated through real-world applications, highlighting its practical value in federated learning scenarios where data heterogeneity poses a significant challenge. A key theoretical contribution is the rigorous analysis demonstrating the algorithm’s convergence properties, including careful management of moving average estimators and non-smoothness of the objective function.
FGDRO-KL Algorithm#
The FGDRO-KL algorithm tackles the challenge of federated group distributionally robust optimization (FGDRO) using a Kullback-Leibler (KL) divergence regularizer. Unlike CVaR-based approaches focusing on worst-case scenarios, FGDRO-KL considers all clients, assigning weights based on their contribution. This is achieved via a clever reformulation that eliminates the constrained primal-dual problem using the KKT conditions, resulting in a three-level compositional structure. The algorithm uses moving averages to estimate gradients efficiently, mitigating the bias inherent in straightforward three-level compositional gradient estimations. This results in reduced communication complexity and sample complexity compared to previous methods. The key innovation lies in the use of moving averages on local machines to approximate global quantities and communicate the summarized parameters. The efficacy is further enhanced through algorithmic strategies. This approach strikes a balance between robustness to distributional shifts across clients and communication efficiency, making it practically suitable for federated learning settings.
Adaptive FGDRO-KL#
An adaptive FGDRO-KL algorithm would likely enhance the standard FGDRO-KL approach by incorporating adaptive learning rates. This would involve adjusting the learning rate for each client or parameter based on its past performance, potentially accelerating convergence and improving performance in non-convex settings. The key challenge would be to design an adaptive mechanism that balances the need for robustness (inherent in the distributional robustness of FGDRO) with responsiveness to individual client data. This could involve carefully weighting updates to avoid overfitting to noisy or atypical client data. A well-designed adaptive method might also address potential issues related to communication efficiency, which is a primary concern of FGDRO. Careful consideration of gradient estimation and communication rounds would be essential to maintain low communication overhead while leveraging the benefits of adaptive optimization. In addition to convergence speed, it’s crucial to analyze whether adaptivity impacts the generalization capability and robustness of the model across various data distributions. Finally, a rigorous theoretical analysis and empirical evaluation would be necessary to fully justify the benefits of this adaptive approach over its non-adaptive counterpart.
Communication Efficiency#
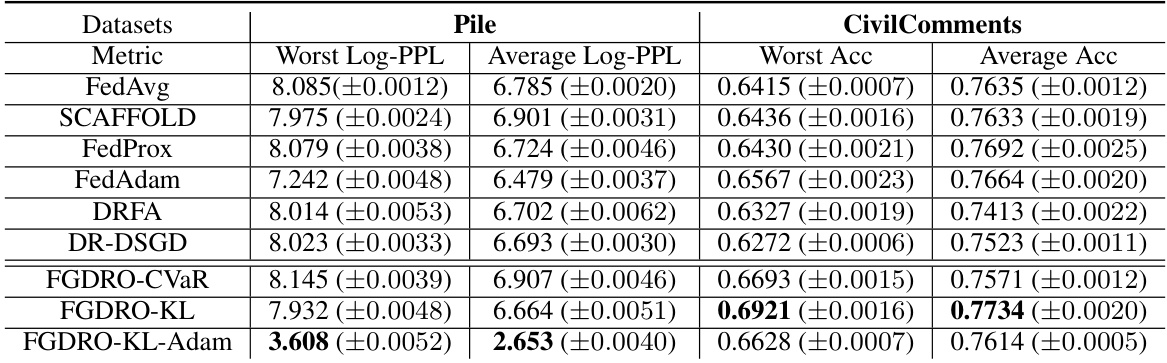
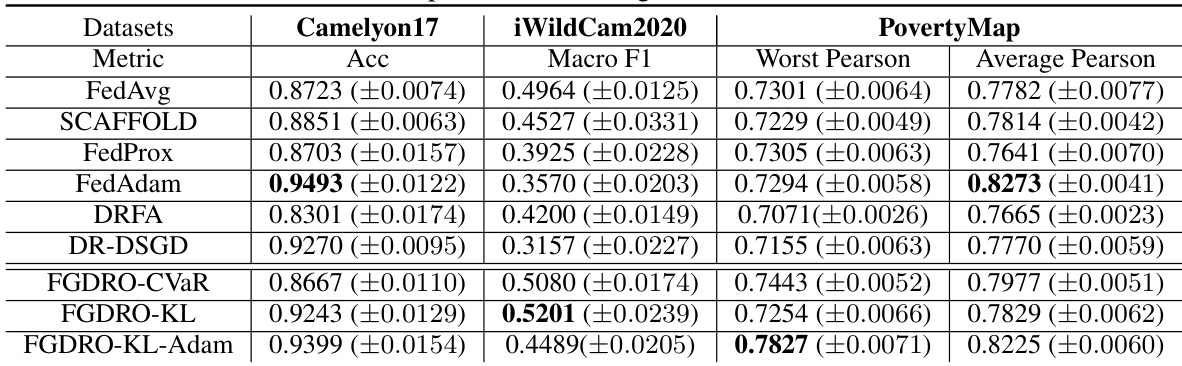
The research paper emphasizes communication efficiency in federated learning, acknowledging the significant communication overhead in traditional approaches. The core issue addressed is the high cost of transmitting model updates between clients and a central server in distributed settings. To improve efficiency, the authors propose algorithms that reduce the amount of data exchanged during each round of communication. This is achieved through techniques such as optimizing the average top-K losses (FGDRO-CVaR), employing KL-regularized FGDRO with moving averages to reduce batch size requirements (FGDRO-KL), and leveraging Adam-type local updates for adaptive learning and potentially surpassing SGD’s performance (FGDRO-KL-Adam). The analysis demonstrates substantial reduction in communication complexity compared to prior methods, achieving costs that scale favorably with the desired precision level (e.g., O(1/ε⁴) for FGDRO-CVaR and O(1/ε³) for FGDRO-KL and FGDRO-KL-Adam). The efficacy of these strategies is validated through experiments on real-world tasks involving natural language processing and computer vision.
Future Work#
Future research directions stemming from this work could explore several promising avenues. Extending the proposed FGDRO algorithms to handle more complex scenarios such as those with non-convex loss functions or time-varying data distributions is crucial. Investigating the theoretical properties of the adaptive algorithms (e.g., convergence rates, stability) under more relaxed assumptions would provide stronger guarantees. Developing efficient methods for handling high-dimensional data within the FGDRO framework is essential for practical applications, especially in settings with resource-constrained devices. Finally, empirical evaluations on a broader range of real-world applications and datasets is warranted to demonstrate the versatility and robustness of the proposed algorithms. These future directions would contribute significantly to advancing the state-of-the-art in communication-efficient federated learning.
More visual insights#
More on figures
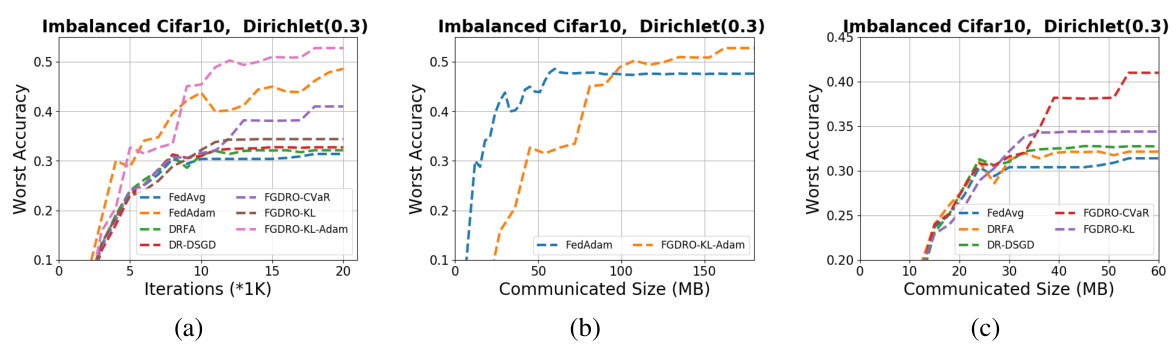
This figure consists of two subfigures. Subfigure (a) shows the impact of varying the communication interval (I) on the performance of FGDRO-CVaR and FGDRO-KL-Adam algorithms on the Camelyon dataset. It demonstrates the robustness of both algorithms to less frequent communication. Subfigure (b) compares the performance of LocalAdam (using Adam-type updates in local steps) against FedAdam (using Adam updates in global steps and SGD in local steps) on the Pile dataset. This highlights the improvement gained by using adaptive steps locally.

This figure consists of two subfigures. Subfigure (a) shows the effect of varying the communication interval (I) on the performance of FGDRO-CVaR and FGDRO-KL-Adam algorithms on the Camelyon dataset. It demonstrates that both algorithms are robust to infrequent communication. Subfigure (b) compares the performance of LocalAdam (an algorithm using Adam updates in local steps) and FedAdam (using Adam updates only in global steps) on the Pile dataset. It shows that LocalAdam outperforms FedAdam, highlighting the benefit of incorporating local Adam updates.
More on tables
This table compares the communication cost and sample complexity of different algorithms for achieving an e-stationary point in federated learning. It contrasts the performance of existing methods (DRFA, DR-DSGD, NDP-SONT) with the proposed algorithms (FGDRO with CVaR constraint and FGDRO with KL regularization). The table shows that the proposed algorithms achieve significantly lower communication and sample complexity compared to the existing ones.
This table compares the communication cost and sample complexity of different algorithms in achieving an e-stationary point (a point where the magnitude of the gradient is less than epsilon). It shows that the proposed algorithms (FGDRO-CVaR and FGDRO-KL) significantly reduce both communication and sample complexity compared to existing methods like DRFA and DR-DSGD. The table also includes the naive deployment of the SONT algorithm as a benchmark for comparison.
This table compares the communication cost and sample complexity of different algorithms in achieving an e-stationary point in federated learning. It contrasts the complexity of existing methods (DRFA, DR-DSGD, NDP-SONT) with the proposed algorithms (FGDRO with CVaR constraint and FGDRO with KL regularization). The table highlights the significant reduction in communication and sample complexity achieved by the proposed algorithms.

This table compares the communication cost and sample complexity of different algorithms for achieving an e-stationary point in federated learning. It shows that the proposed algorithms (This Work) significantly reduce both communication and sample complexity compared to existing methods (DRFA [11], DR-DSGD [30], NDP-SONT [22]). The table highlights the differences based on whether a CVaR constraint or a KL regularization is used. The sample complexity measures the amount of data needed by each machine, while communication complexity refers to the number of communications needed to converge to a solution.

This table compares the communication cost and sample complexity of different algorithms for solving the Federated Group Distributionally Robust Optimization (FGDRO) problem. It shows the complexity of achieving an e-stationary point or near e-stationary point for various algorithms, including the proposed algorithms (FGDRO-CVaR and FGDRO-KL) and existing methods such as DRFA, DR-DSGD, and NDP-SONT. The complexity is measured in terms of the order of communication rounds and number of samples required on each machine to reach the desired precision level (e).
This table compares the communication cost and sample complexity of different algorithms for achieving an e-stationary point in federated learning. It contrasts the performance of existing methods (DRFA, DR-DSGD, NDP-SONT) with the proposed algorithms (FGDRO with CVaR and KL regularizers). The table highlights the significant reduction in communication and sample complexity achieved by the proposed algorithms, showcasing their efficiency in federated group distributionally robust optimization.

This table compares the communication cost and sample complexity of different algorithms for achieving an e-stationary point in federated learning. It contrasts the proposed methods (FGDRO-CVaR and FGDRO-KL) with existing state-of-the-art techniques, highlighting the significant reduction in communication and sample complexity achieved by the proposed algorithms. The table also shows the sample complexity on each machine, which is the number of samples required to achieve the desired precision level.

This table compares the communication cost and sample complexity of various algorithms for solving the Federated Group Distributionally Robust Optimization (FGDRO) problem. It shows the complexity for achieving an e-stationary point (or near e-stationary point) under different regularization methods (CVaR and KL) and existing methods (DRFA, DR-DSGD, NDP-SONT). The table highlights the communication and sample complexity improvements of the proposed algorithms (FGDRO-CVaR and FGDRO-KL).
This table compares the communication cost and sample complexity of different algorithms for achieving an e-stationary point or near e-stationary point in federated learning. It shows the complexity for each machine to achieve a (sub)gradient norm less than epsilon squared. The algorithms compared include DRFA [11], DR-DSGD [30], NDP-SONT [22], and the proposed algorithms FGDRO-CVaR and FGDRO-KL. The table highlights the significant reduction in communication and sample complexity achieved by the proposed algorithms.
Full paper#