Infinite-Dimensional Feature Interaction

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers because it introduces a novel approach to neural network design by leveraging infinite-dimensional feature interactions. This addresses the limitations of existing methods that primarily capture low-order interactions, opening new avenues for improving model performance and deepening our understanding of feature representation learning. Its findings are relevant to current research trends in deep learning, especially those focusing on attention mechanisms and high-order interactions.

Visual Insights

#

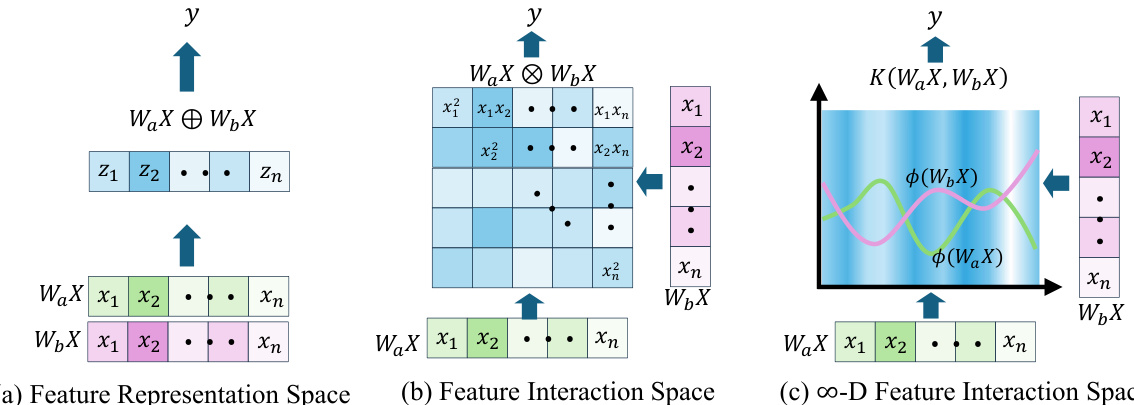
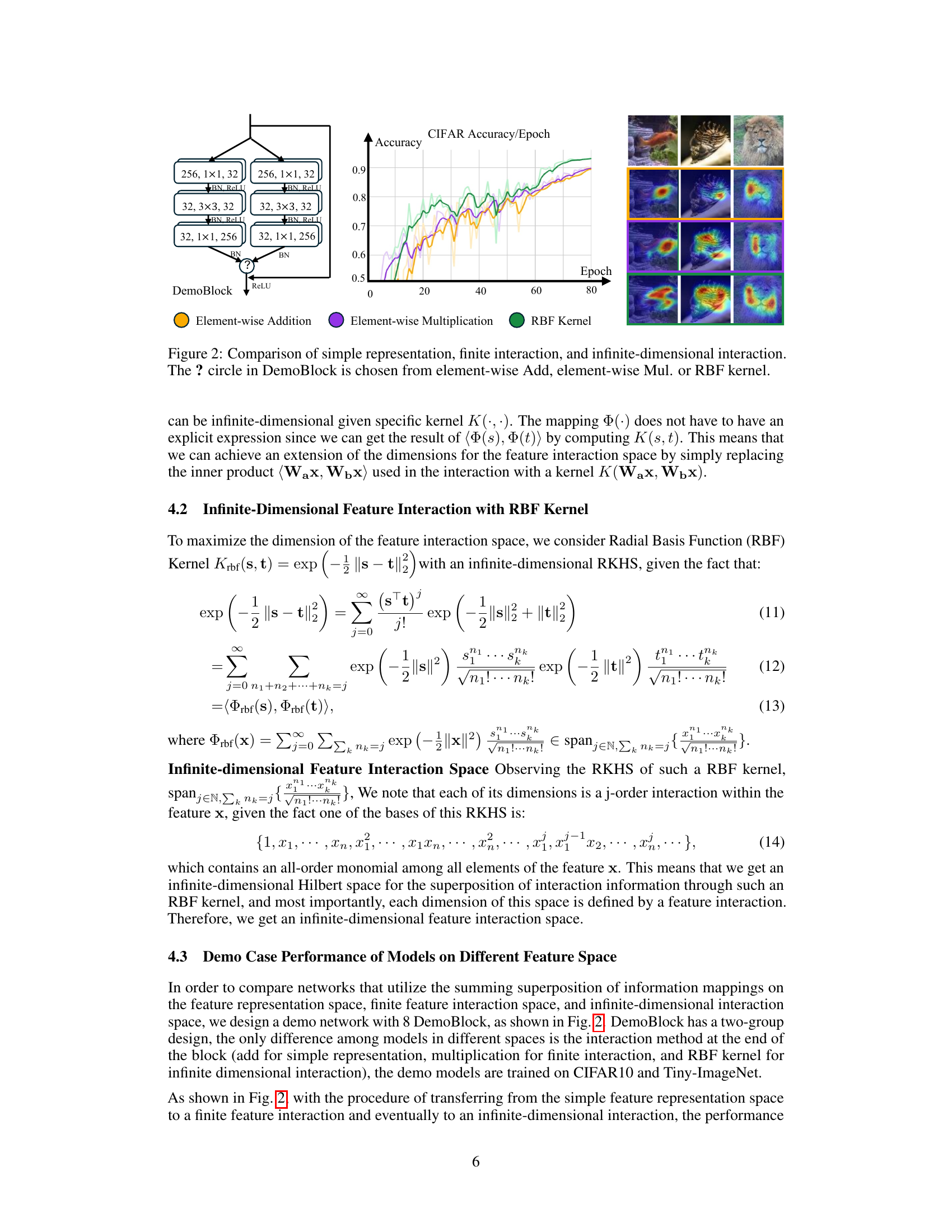
This figure illustrates three different approaches to feature interaction in neural networks. (a) shows the traditional approach, where features are simply linearly combined. (b) shows a more modern approach, where element-wise multiplication is used to create higher-order feature interactions. (c) shows the proposed approach, which uses a kernel function to implicitly map features to an infinite-dimensional space, allowing for much richer interactions.

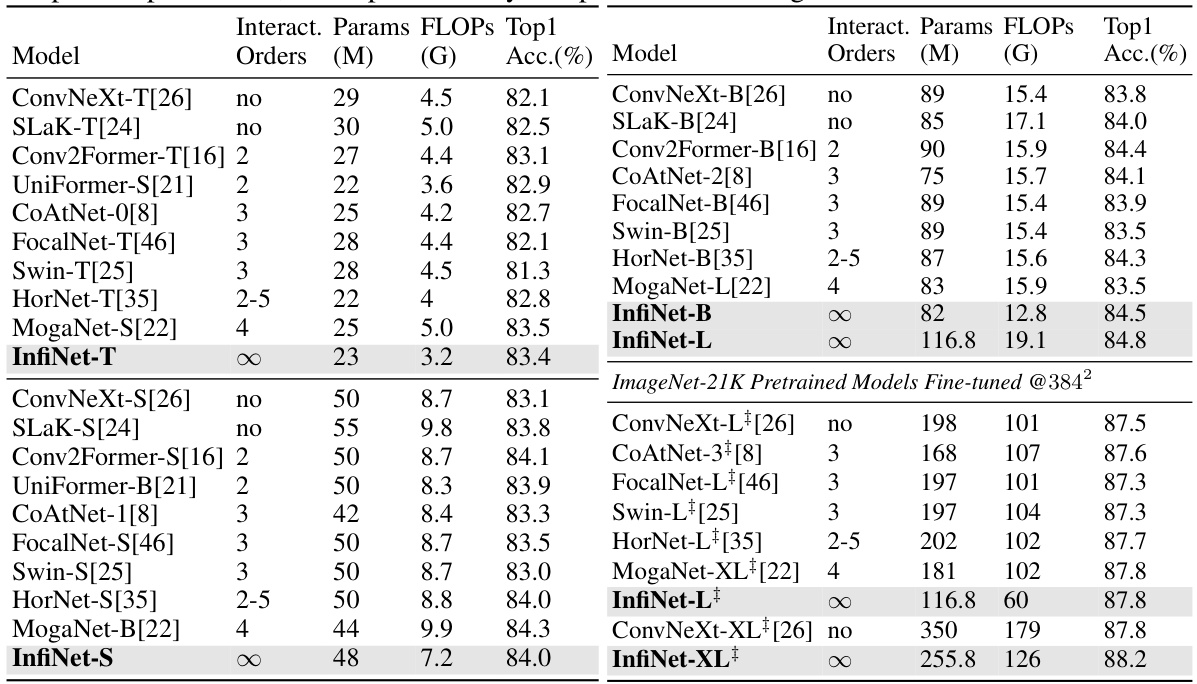
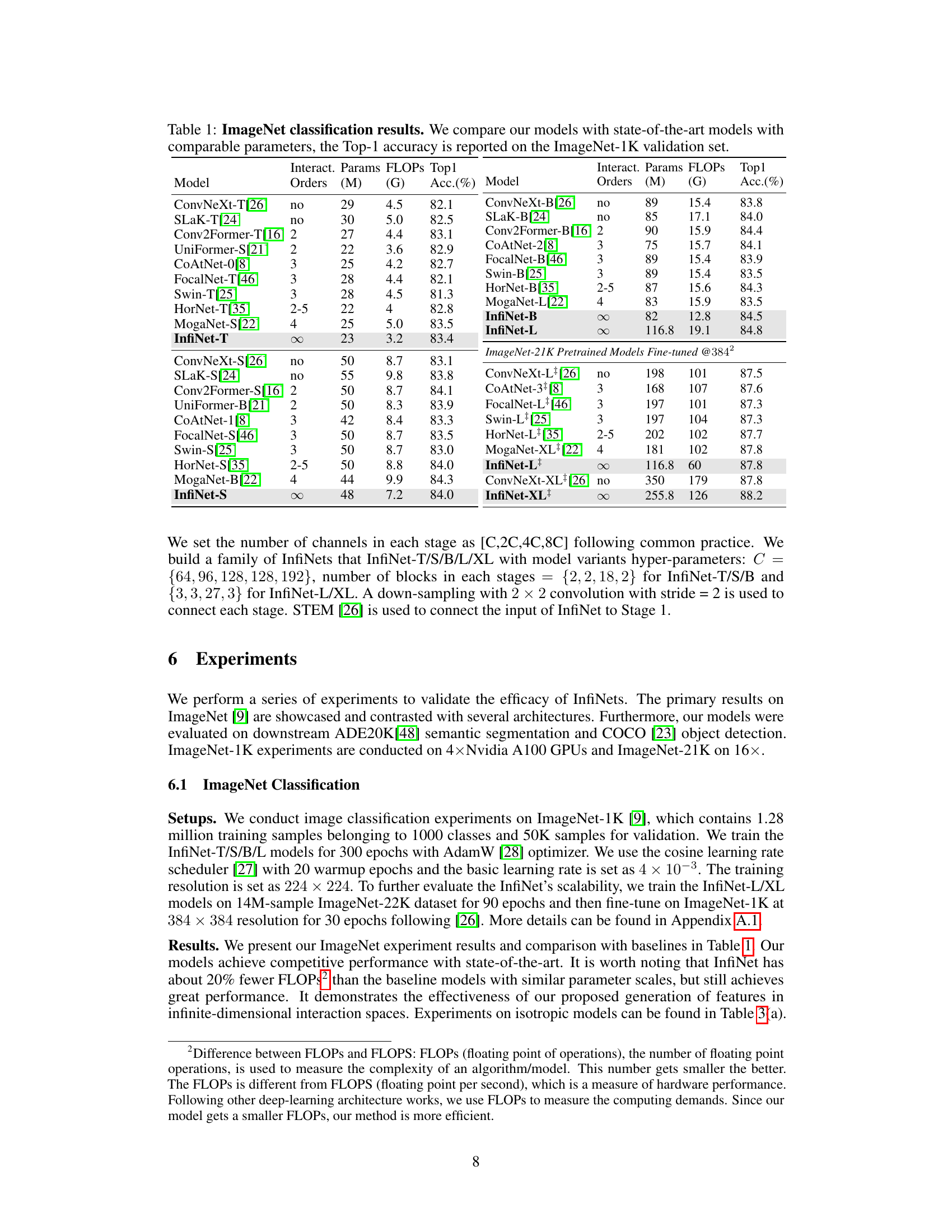
This table presents the ImageNet-1K validation results for various state-of-the-art models and the proposed InfiNet models. It compares the Top-1 accuracy, number of parameters (in millions), and FLOPs (in billions) for each model. The models are categorized by the type of feature interaction they utilize (no interaction, finite-order interaction, and infinite-dimensional interaction using the InfiNet approach). This comparison helps to demonstrate the performance gains achieved by InfiNet’s infinite-dimensional feature interaction.

In-depth insights

#

InfiNet Architecture

#

The InfiNet architecture is a novel approach to neural network design that leverages infinite-dimensional feature interaction to significantly enhance model performance. It departs from traditional architectures that primarily focus on scaling the feature representation space (width and depth) by instead concentrating on the feature interaction space. InfiNet achieves this through the innovative use of radial basis function (RBF) kernels, replacing element-wise multiplication common in attention mechanisms and other interaction-based techniques. This kernel-based approach implicitly maps features into an infinite-dimensional space, facilitating significantly richer and more nuanced interactions between features than is possible with finite-dimensional methods. The core building block of InfiNet is the InfiBlock, which efficiently incorporates RBF kernels, balancing complexity with performance gains. The hierarchical architecture of InfiNet, with InfiBlocks stacked across multiple stages, allows for the effective capture of intricate high-order feature relationships across the entire model. This design choice demonstrates a sophisticated understanding of the limitations of traditional approaches and proposes a powerful alternative for tackling complex tasks in computer vision.

Kernel Feature Map

#

A ‘Kernel Feature Map’ in the context of deep learning suggests a transformation of the feature space using kernel methods. Instead of relying on explicit weight matrices for feature interactions (like in convolutional layers), it leverages kernel functions to implicitly map the features into a potentially high-dimensional space, where interactions are computed via inner products in this new space. This approach offers several advantages: it allows for modeling complex, non-linear relationships between features efficiently, which is often computationally expensive with explicit methods; it can capture higher-order interactions more naturally, going beyond pairwise interactions; and it provides flexibility in choosing appropriate kernels depending on the specific task and data properties. However, the computational cost of kernel computations can be high, especially for large datasets, therefore efficient approximations are crucial for practical implementations. The choice of kernel itself is also critical, as it determines the properties of the resulting feature space, affecting model performance and generalization. Furthermore, understanding the interpretability of the learned feature map in the kernel space remains a significant challenge. Therefore, a careful selection of the kernel function, consideration of computational cost, and investigation of the resulting feature representation’s properties are key factors in designing and applying a successful kernel feature map approach.

Interaction Scaling

#

The concept of ‘Interaction Scaling’ in deep learning architectures focuses on how the capacity for feature interactions grows with model size. Traditional designs, relying on linear combinations, have limited interaction space. Element-wise multiplication, while enhancing interactions, remains constrained to low-order interactions within a finite-dimensional space. The paper argues for moving beyond this limitation by leveraging techniques from kernel methods to create infinite-dimensional interaction spaces. This approach allows the model to implicitly capture high-order feature dependencies and complex relationships, enabling more expressive representation learning. The use of RBF kernels is particularly highlighted for its ability to achieve this infinite-dimensional scaling. The key benefit lies in its capability to generate theoretically infinite-dimensional feature interactions, offering an improvement over element-wise multiplication’s limited representation and leading to enhanced model performance. However, efficient computation within such high-dimensional spaces remains a challenge, and further research into optimization techniques is needed.

Ablation Studies

#

Ablation studies systematically remove or alter components of a model to assess their individual contributions. In the context of a research paper focusing on infinite-dimensional feature interactions, ablation studies would be crucial for demonstrating the efficacy of the proposed approach. One key aspect would involve comparing models trained with finite-order feature interactions against those using the infinite-dimensional interaction method. This would reveal whether the improvement in performance is primarily due to the infinite-dimensional space or other design choices. Another important ablation would test the impact of different kernel functions (e.g., RBF, polynomial). This helps determine if the benefits are specific to the chosen kernel or if the infinite-dimensional paradigm generally offers advantages. Furthermore, studies examining variations in the network architecture (e.g., number of layers, filter sizes) while holding the infinite-dimensional interaction component constant will evaluate the robustness and generalizability of the approach. Finally, analysis of the computational cost of different components will demonstrate the efficiency gains (or trade-offs) of utilizing infinite-dimensional interactions. Overall, well-designed ablation studies are critical for confirming that the observed performance improvements are directly attributable to the infinite-dimensional feature interaction space and not other factors, ultimately strengthening the paper’s claims.

Future Works

#

Future work directions stemming from this infinite-dimensional feature interaction research could explore several promising avenues. Extending the kernel methods beyond RBF to encompass a broader range of kernels (e.g., polynomial, Laplacian) could reveal performance improvements or adaptability to various data types. Investigating alternative architectures for infinite-dimensional interaction besides the proposed InfiNet is crucial to establish the generality of the findings. Furthermore, the impact of different hyperparameters within the RBF kernel (such as the gamma parameter) requires a more thorough investigation. Exploring the effectiveness of InfiNet on more complex vision tasks, such as video understanding, and adapting it to other modalities like natural language processing would demonstrate its wider applicability and robustness. Finally, examining the potential of combining infinite-dimensional interactions with other advanced techniques, like self-supervised learning or model compression, could unlock further performance gains or address scalability concerns.

More visual insights

#

More on figures

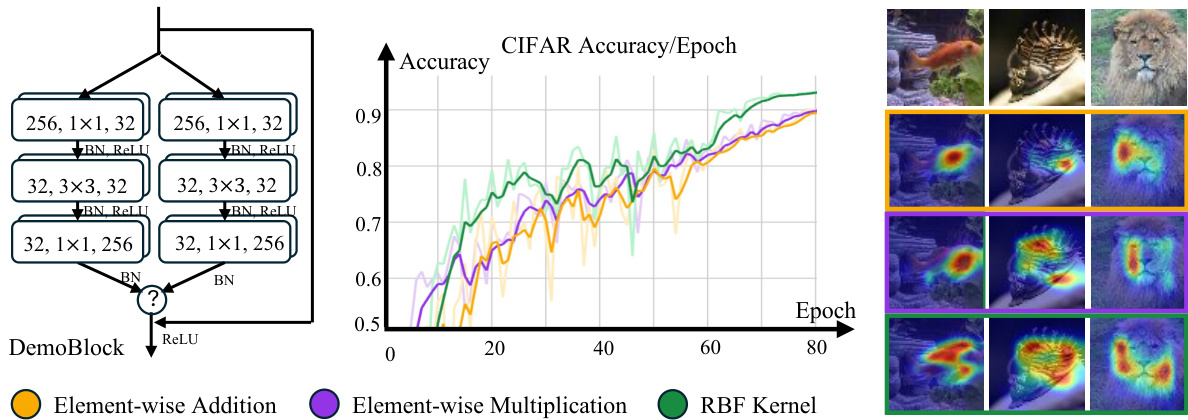
This figure compares three different approaches to feature interaction in a neural network: simple representation (element-wise addition), finite interaction (element-wise multiplication), and infinite-dimensional interaction (RBF kernel). The left panel shows the architecture of a ‘DemoBlock,’ which is a building block within a larger network. The block comprises several convolutional layers and batch normalization, culminating in a choice of one of the three interaction methods represented by the question mark. The right panel shows the accuracy curves obtained when training these different architectures on the CIFAR dataset. The graph shows a steady increase in performance when moving from simple representation to finite and then to infinite-dimensional interactions. The bottom panel shows example visualizations of the class activation maps generated by each method, highlighting the differences in how the models interpret the features. The RBF kernel is shown to produce the most comprehensive class activation map.

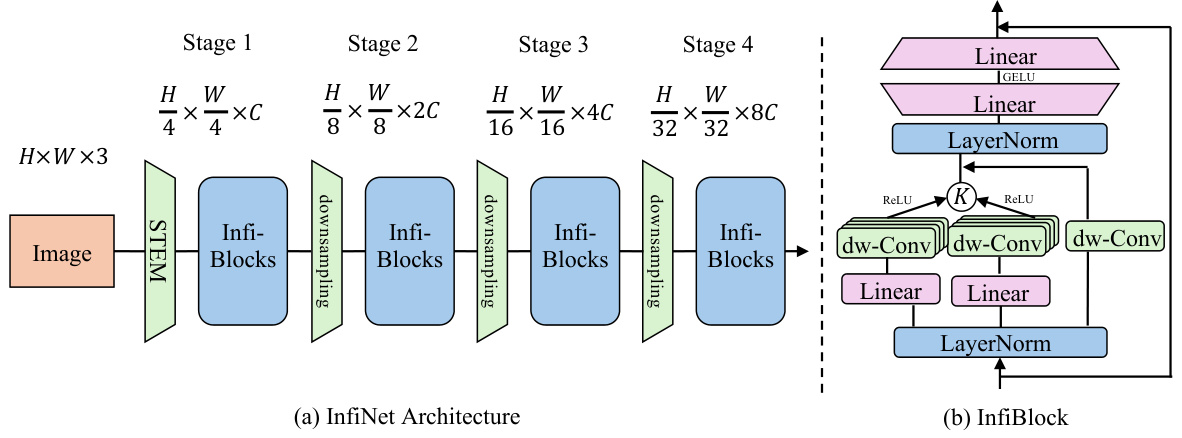
This figure provides a detailed overview of the InfiNet architecture. (a) shows the overall hierarchical structure of InfiNet, consisting of four stages with increasing feature map resolutions and channel counts. Each stage comprises multiple InfiBlocks, which are the building blocks of the network. (b) illustrates the design of a single InfiBlock, showcasing the key components involved in its infinite-dimensional feature interaction mechanism, such as LayerNorm, depth-wise convolutions (dw-Conv), ReLU activations, RBF kernel for feature interaction, and MLP layers. This detailed visualization helps clarify how InfiNet leverages infinite-dimensional feature interactions within a hierarchical framework to achieve state-of-the-art performance.

This figure presents a visual comparison of three different models’ class activation maps (CAMs). CAMs are heatmaps that highlight the regions of an image that are most influential in a model’s prediction. The three models compared are: (1) A traditional model focusing solely on feature representation space, showing limited attention across the image; (2) A model utilizing finite feature interaction, indicating some improvement in focusing on relevant parts of the image; and (3) InfiNet, the proposed infinite-dimensional feature interaction model, demonstrating a much more focused and precise activation map, correctly emphasizing the key object features in each image. The comparison visually highlights the effectiveness of the InfiNet’s approach in capturing more complete and accurate spatial relationships in an image for classification.

More on tables

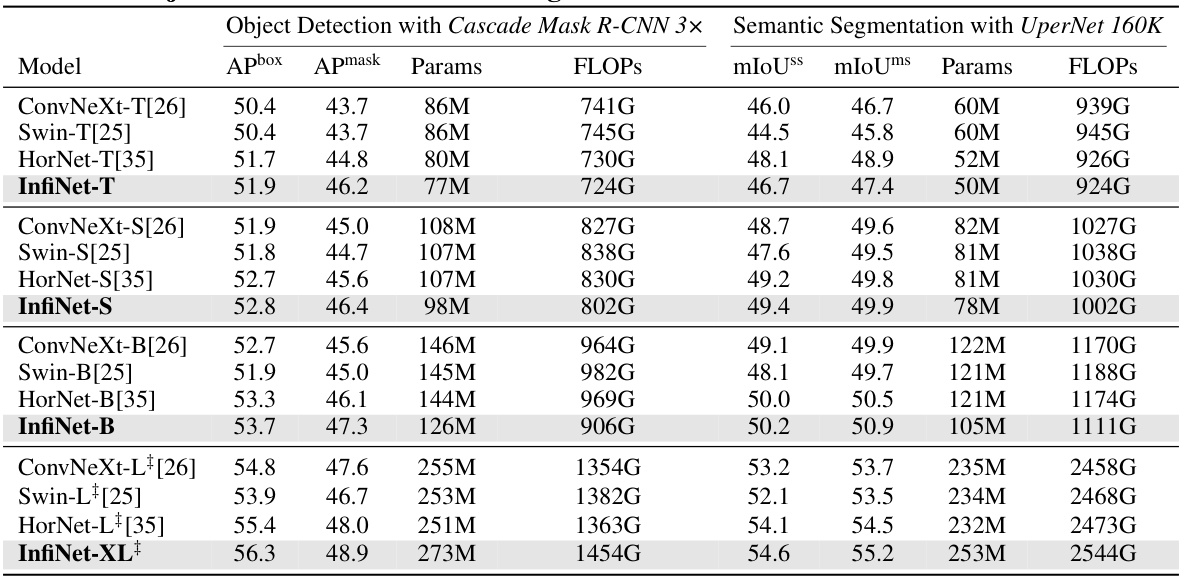
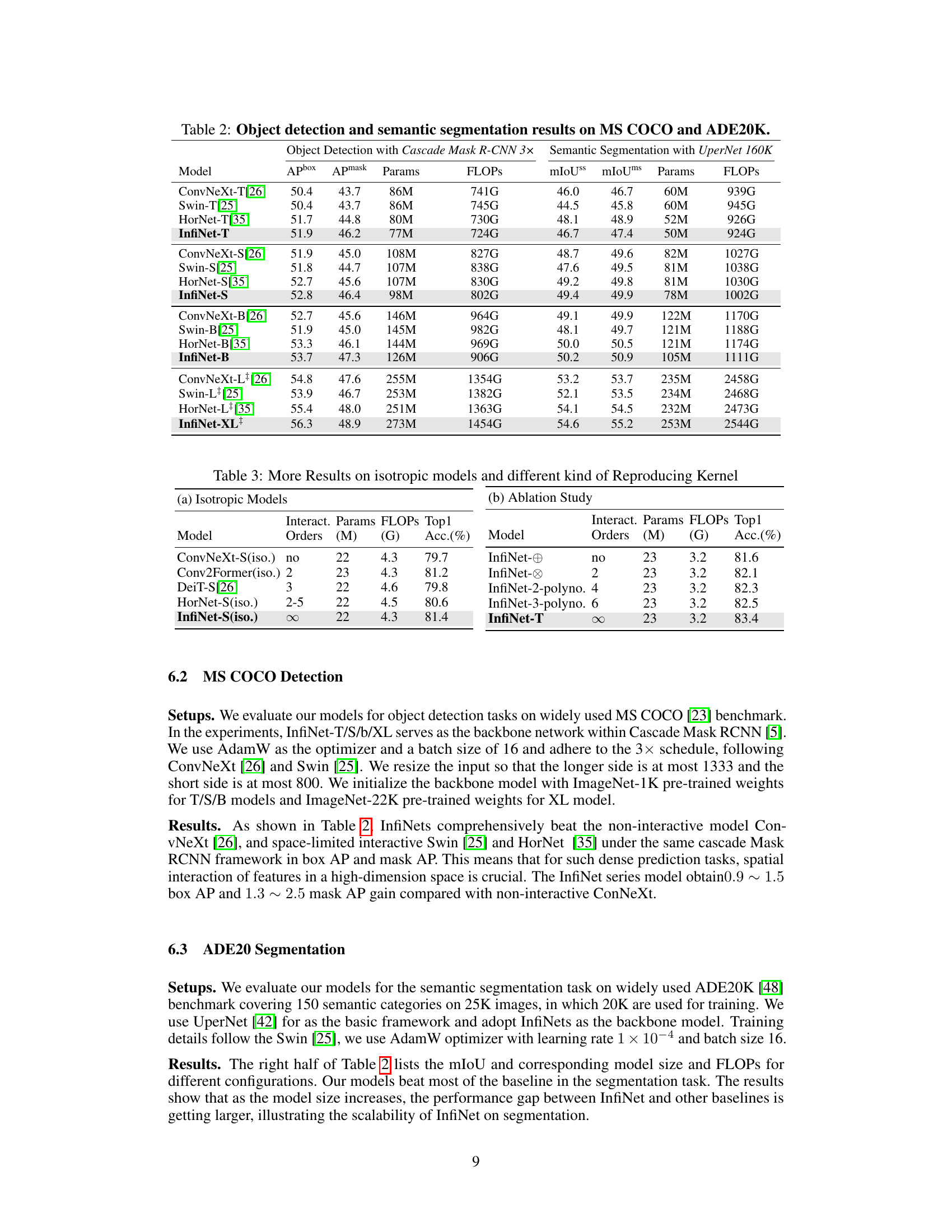
This table presents a comparison of the performance of different models on object detection and semantic segmentation tasks using the MS COCO and ADE20K datasets. The models compared include various versions of ConvNeXt, Swin, and HorNet, along with the InfiNet model proposed in the paper. For each model, the table shows the results in terms of box AP, mask AP, mIoU (mean Intersection over Union), and the number of parameters (Params) and FLOPS (floating-point operations). The results demonstrate the superior performance of InfiNet compared to the baseline models, particularly for the larger models.

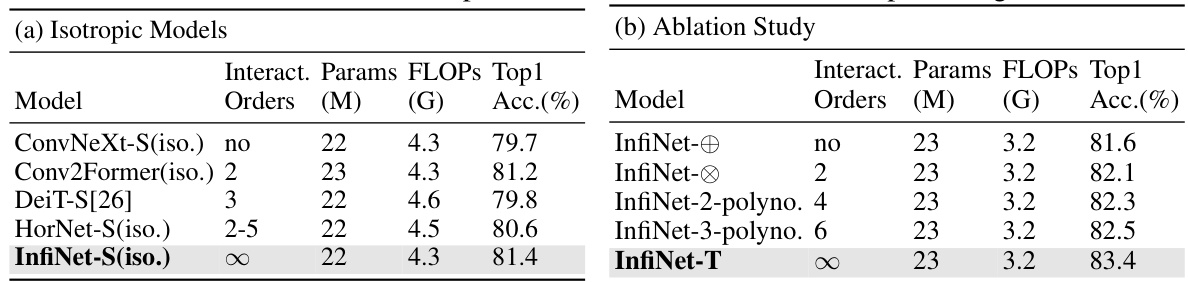
This table presents the results of experiments conducted using isotropic models and different reproducing kernels. It compares the performance of various models (ConvNeXt-S, Conv2Former, DeiT-S, HorNet-S, and InfiNet-S) with different interaction orders (none, 2, 3, 2-5, and infinity). The ablation study section focuses on the InfiNet architecture, testing the impact of changing the kernel’s order (none, 2, 4, and 6) on performance, and comparing it against the original InfiNet-T model. Both sections report the parameters (M), FLOPs (G), and Top-1 accuracy (%).

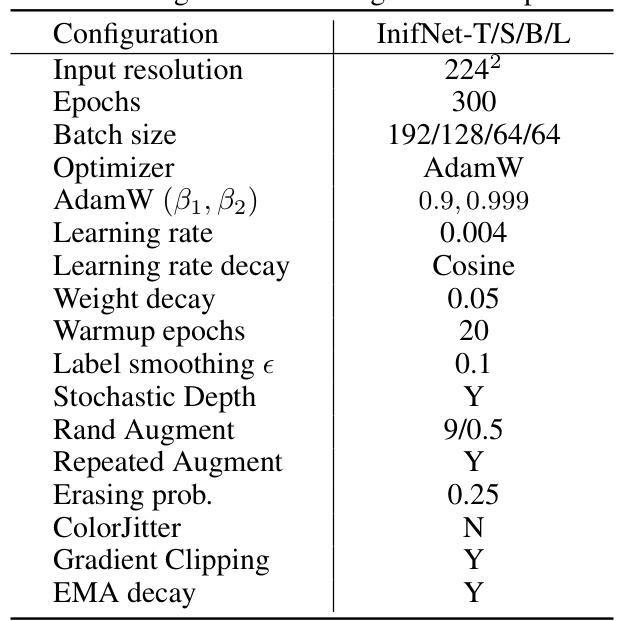
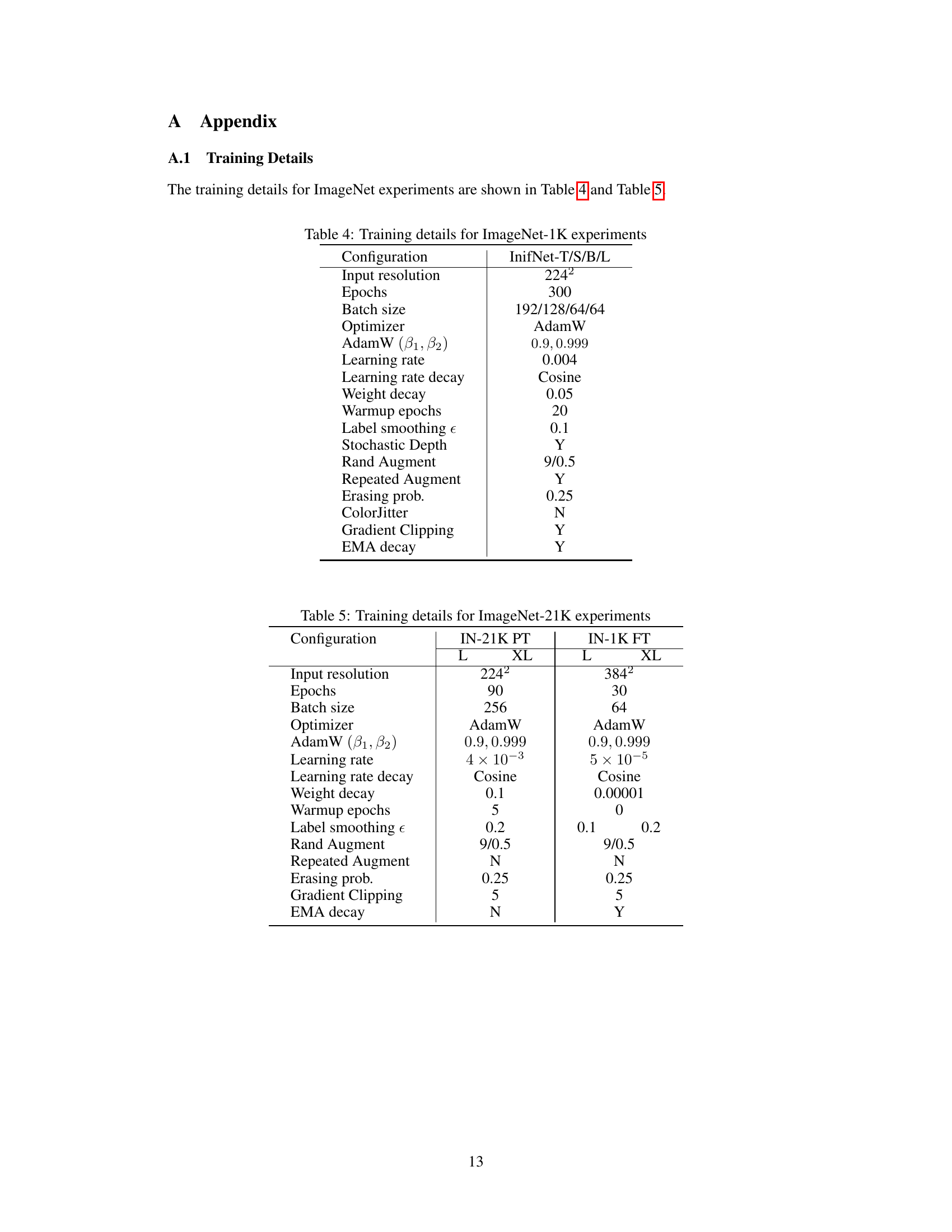
This table details the training configurations used for the ImageNet-1K experiments in the paper. It lists various hyperparameters, optimization techniques, data augmentation strategies, and regularization methods employed during training.

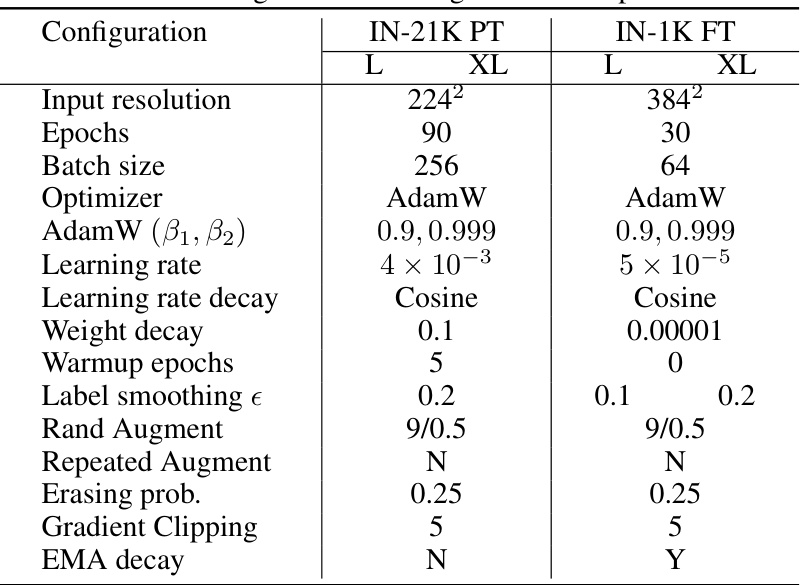
This table compares the performance of the proposed InfiNet models with several state-of-the-art models on the ImageNet-1K dataset. It shows the Top-1 accuracy, the number of model parameters (in millions), and the number of floating point operations (in billions). The table is divided into two sections: models trained only on ImageNet-1K and models pre-trained on ImageNet-21K and then fine-tuned on ImageNet-1K. For each model, the table indicates whether it uses interaction of orders 0, 2, 3, 2-5, 4, or infinite, highlighting the impact of different interaction mechanisms on performance.

Full paper

#