↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Uncertainty quantification (UQ) in graphical models is crucial for reliable decision-making, but existing sampling-based methods are slow and existing fast methods underestimate uncertainty. This paper tackles these issues.
The proposed method, LinUProp, uses linear uncertainty propagation to model uncertainty additively. This provides linear scalability, guaranteed convergence, and closed-form solutions. LinUProp’s accuracy is validated through theoretical analysis and experiments, showcasing its superiority over existing methods in uncertainty-based active learning.
Key Takeaways#
Why does it matter?#
This paper is important because it introduces LinUProp, a novel method for uncertainty quantification in graphical models that offers linear scalability, guaranteed convergence, and closed-form solutions without underestimating uncertainty. This addresses a critical limitation of existing methods, paving the way for more reliable and efficient decision-making in various applications involving complex data dependencies. The theoretical analysis and experimental results demonstrate LinUProp’s superiority, opening new avenues for uncertainty-based active learning and improving the trustworthiness of graphical model inferences.
Visual Insights#

This figure illustrates how existing methods (NETCONF and SocNL) underestimate uncertainty when dealing with nodes having uncertain neighbors. It compares their approach to the proposed LinUProp method. LinUProp uses interval widths to represent uncertainty, showing how uncertainty increases additively with more neighbors, unlike the multiplicative approach of existing methods. The figure also highlights the interpretability of LinUProp by visually showing the contribution of each neighbor’s uncertainty to the overall uncertainty.
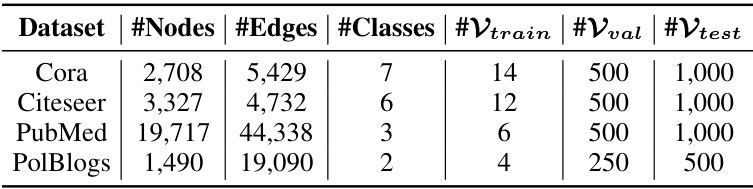
This table presents the statistical information and partitioning of four datasets used in the paper’s experiments. It shows the number of nodes, edges, and classes for each dataset, along with the sizes of the training, validation, and test sets used in the effectiveness experiments. The remaining nodes are in Vulp, which are unlabeled nodes and used in the active learning experiments.
In-depth insights#
Linear UQ Method#
The proposed “Linear UQ Method” offers a novel approach to uncertainty quantification (UQ) in graphical models, addressing limitations of existing sampling-based and closed-form methods. Linearity is achieved by propagating uncertainty additively rather than multiplicatively, leading to improved accuracy and avoidance of underestimation, particularly in scenarios with high uncertainty or noisy data. This linear propagation simplifies calculations and guarantees convergence, resulting in greater scalability compared to sampling techniques, suitable for large-scale graph datasets. The method also provides interpretability by tracking uncertainty contributions from individual nodes and edges, offering insights for decision-makers and enhancing trust in the UQ process. A significant theoretical contribution is the demonstration that the method’s computed uncertainty represents the generalized variance component of the model’s prediction error, providing a strong foundation for its reliability and accuracy. Closed-form solution further adds to its efficiency.
Scalable Uncertainty#
Scalable uncertainty quantification in machine learning models, especially for complex graphical models, is crucial for building trustworthy AI systems. Existing methods often struggle with scalability, particularly when dealing with large datasets and complex relationships. Sampling-based approaches are accurate but computationally expensive, while closed-form methods might be faster but often underestimate uncertainty. Therefore, developing techniques that balance accuracy and efficiency is a critical challenge. A promising direction involves leveraging the structure of the data, such as the sparsity in graphical models or the hierarchical relationships in datasets, to design more efficient algorithms. Linear approximations or iterative methods can be employed to significantly reduce computational costs without sacrificing too much accuracy. Another important aspect is interpretability: understanding the sources and magnitudes of uncertainties is vital for decision-making. Developing methods that not only quantify uncertainty scalably but also offer insights into the factors driving uncertainty is a critical area of ongoing research. This will allow practitioners to better trust and utilize the uncertainty estimates for more effective decision-making in high-stakes applications.
Interpretable UQ#
Interpretable Uncertainty Quantification (UQ) is crucial for building trust and facilitating effective decision-making in complex systems. Many UQ methods exist, but interpretability often lags behind. A user needs to understand not just the magnitude of uncertainty, but also its source and contributing factors. This is especially important for applications like medical diagnosis or financial modeling, where consequences of errors can be significant. The goal of interpretable UQ is to make uncertainty results transparent and understandable, perhaps by visualizing uncertainty in a way that aligns with human cognitive processes or by explicitly connecting uncertainty measures to the model’s input features and underlying assumptions. This requires developing novel methods or adapting existing techniques to provide explainable outputs and visualizations that are easy for users to grasp and validate. Achieving interpretable UQ is a key step towards bridging the gap between sophisticated data analysis and human comprehension, enabling more informed and responsible use of complex models.
Active Learning#
Active learning, a crucial aspect of machine learning, is thoughtfully explored in this research paper. The core idea revolves around strategically selecting the most informative data points for labeling, thus maximizing the learning efficiency. This contrasts with passive learning, which relies on randomly selected data. The paper likely demonstrates how uncertainty quantification (UQ) plays a vital role in this process, enabling the algorithm to prioritize data points with high uncertainty. This approach not only reduces labeling costs but also potentially enhances the model’s overall accuracy and robustness. LinUProp, the proposed UQ method, likely serves as the foundation for active learning, providing a computationally efficient way to estimate the uncertainty associated with predictions, thereby guiding the selection of the next data points to label. The experimental results section likely showcases the effectiveness of this approach, comparing LinUProp’s performance against other existing methods on various real-world graph datasets. Superior performance in terms of accuracy with a reduced labeling budget would strongly support the effectiveness of LinUProp-guided active learning. The authors likely discuss the implications of their findings for practical applications, highlighting the potential of LinUProp to optimize resource allocation and improve the overall performance of machine learning models in data-scarce environments.
Future Research#
Future research directions stemming from this work could explore extending LinUProp’s applicability to more complex graphical model structures, such as those with higher-order interactions or non-symmetric compatibility matrices. Investigating the impact of different linearization techniques on accuracy and efficiency would also be valuable. A crucial next step is a comprehensive empirical comparison with a wider range of state-of-the-art UQ methods across diverse datasets, including those with different noise characteristics. Additionally, exploring the potential of integrating LinUProp with explainable AI (XAI) techniques is promising, allowing users to better understand the sources of uncertainty and their impact on decisions. Finally, theoretical work on proving tighter bounds on the convergence rate of LinUProp and analyzing its performance under various graph properties is needed.
More visual insights#
More on figures

This figure illustrates how LinUProp calculates uncertainty in a simple 3-node graph. It shows how the uncertainty in the prior beliefs (interval widths e1, e2, e3) and the edge potentials (matrices H12 and H23) are used to compute the uncertainty in the posterior beliefs (interval widths in vec(B)). The key highlight is LinUProp’s ability to handle different compatibility matrices for each edge, a feature not present in previous methods.

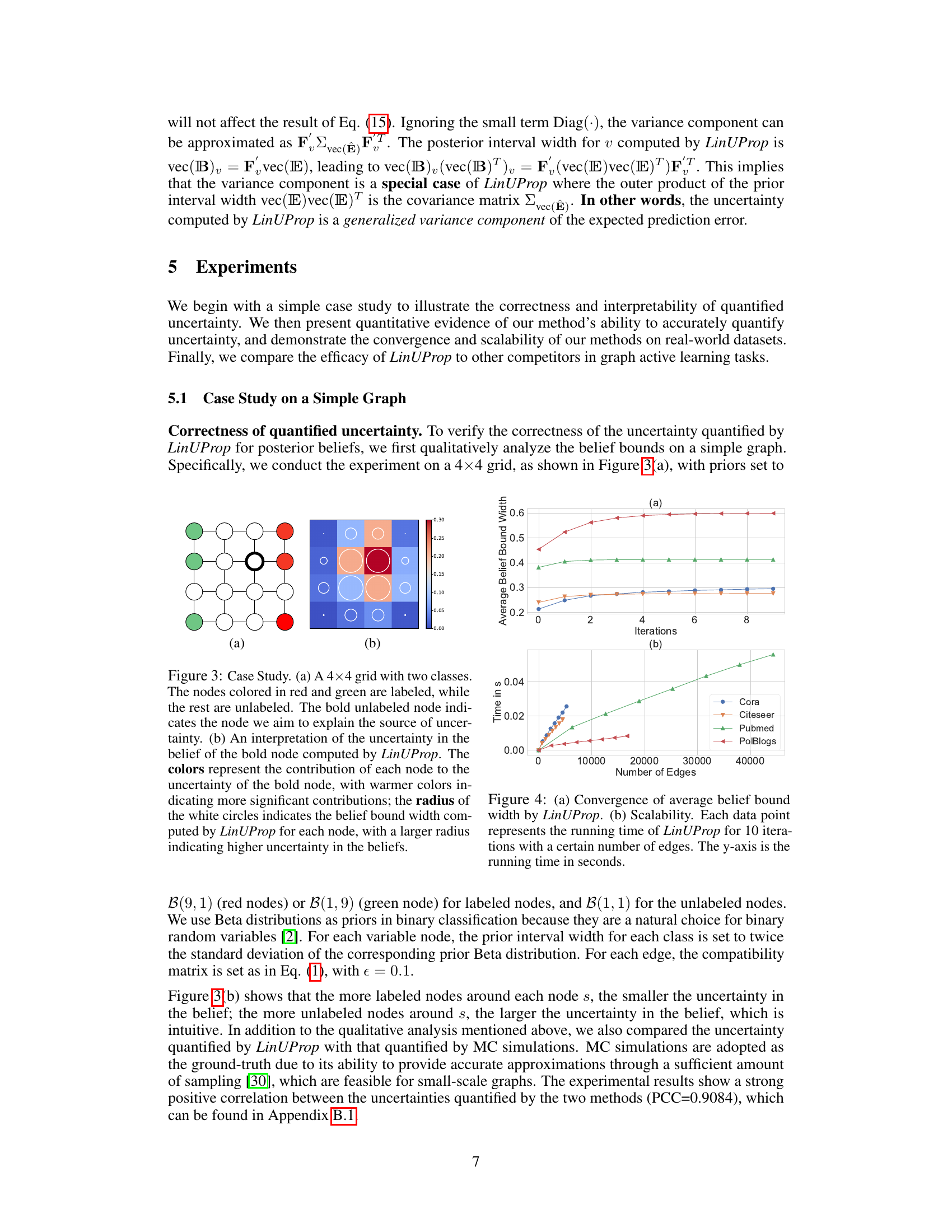
This figure shows a case study on a 4x4 grid graph with two classes. Part (a) illustrates the graph structure, with labeled nodes (red and green) and unlabeled nodes (white), highlighting a specific unlabeled node for analysis. Part (b) visually represents the uncertainty in the belief of that highlighted node as computed by LinUProp. The color intensity shows the contribution of each neighboring node to the overall uncertainty, while the circle size corresponds to the magnitude of the uncertainty associated with each node.

This figure presents the convergence and scalability results of the LinUProp algorithm. The top panel (a) shows the convergence of the average belief bound width across different datasets (Cora, Citeseer, Pubmed, Polblogs), demonstrating that the algorithm reaches convergence within approximately 10 iterations for all datasets. The bottom panel (b) demonstrates the linear scalability of LinUProp by plotting the running time (in seconds) against the number of edges in the graph for each dataset. The linear relationship between running time and the number of edges confirms that the LinUProp algorithm exhibits linear scalability.

This figure compares the performance of different node selection strategies in active learning, using belief propagation for inference. The strategies are compared across four datasets (Cora, Citeseer, Pubmed, PolBlogs) at various labeling budgets. LinUProp and its variant (LC+BB) consistently show higher test accuracy than random selection, least confidence, and entropy-based selection.

This figure shows the test accuracy for different labeling budgets on four datasets (Cora, Citeseer, PubMed, Polblogs) using Belief Propagation (BP) for posterior belief inference. Different node selection strategies are compared: Random, Least Confidence (LC), Entropy, Belief Bound (BB) from LinUProp, LC+BB (combination of LC and BB), Certainty Score (CS) from NETCONF, and LC+CS (combination of LC and CS). The results demonstrate that LinUProp-based strategies generally achieve higher test accuracy with the same labeling budget, showcasing its effectiveness in active learning.
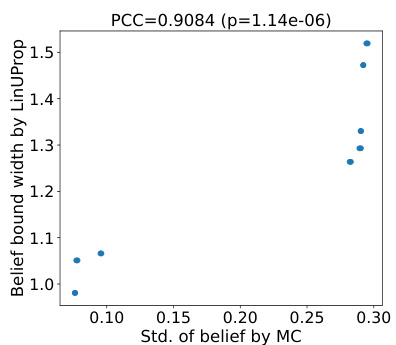
This figure shows a strong positive correlation between the uncertainties computed by Monte Carlo (MC) simulation and LinUProp. The x-axis represents the empirical standard deviation from MC simulation, approximating the ground truth uncertainty, and the y-axis represents the uncertainty from LinUProp. The high correlation (PCC = 0.9084) validates the accuracy of LinUProp in quantifying uncertainty.

The figure shows the test accuracy for various labeling budgets when using belief propagation (BP) to infer posterior beliefs. It compares different node selection strategies, highlighting the performance of LinUProp and its variant against random selection, least confidence, and entropy-based selection methods. The results are shown for different datasets and labeling accuracies. Higher test accuracy indicates better performance.

This figure shows the test accuracy for different labeling budgets when using belief propagation (BP) to infer posterior beliefs. The x-axis represents the size of the labeling budget, and the y-axis shows the test accuracy. Different colors represent different node selection strategies (Random, Least Confidence, Entropy, Belief Bound (LinUProp), and a combination of Least Confidence and Belief Bound). The shaded areas indicate the standard deviation across multiple trials. The figure demonstrates that LinUProp-based strategies consistently achieve higher test accuracy with smaller labeling budgets, particularly when the labeling accuracy is high.
More on tables
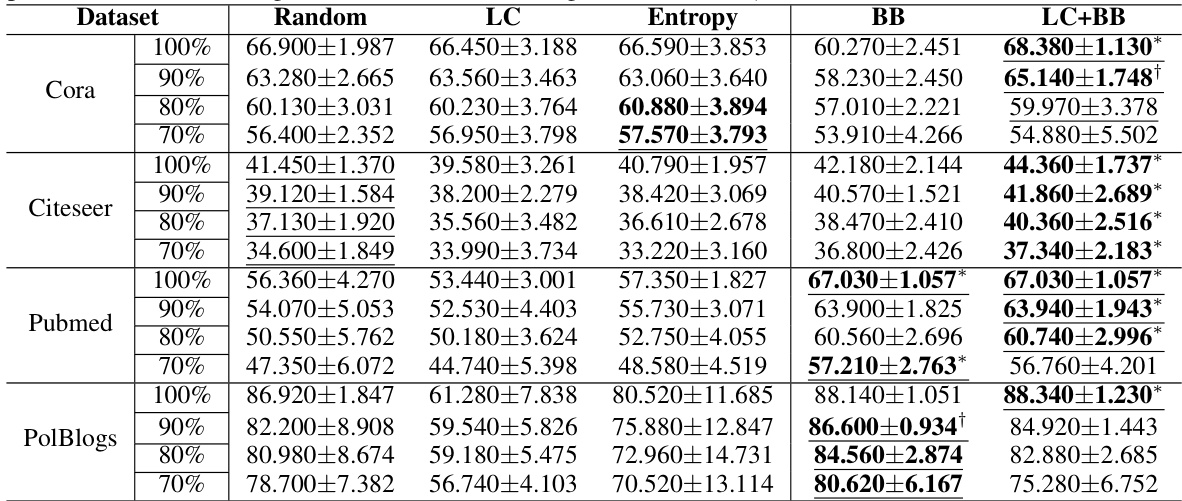
This table presents the mean test accuracy and standard deviation for a fixed labeling budget of 20b, using noisy labels and BP for inference. It compares different node selection strategies, highlighting the superior performance of LinUProp-based methods (BB and LC+BB) across various datasets and labeling accuracies.
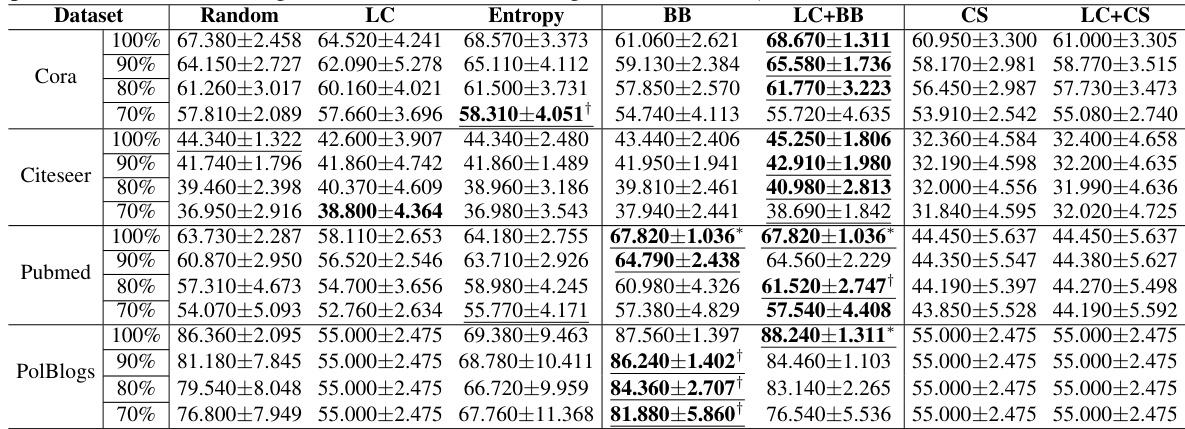
This table presents the mean test accuracy and standard deviation for different node selection strategies (Random, LC, Entropy, BB, LC+BB) using a fixed labeling budget of 20b. The results are shown for four datasets (Cora, Citeseer, Pubmed, Polblogs) and four labeling accuracies (70%, 80%, 90%, 100%). Statistical significance is indicated using * and † symbols.
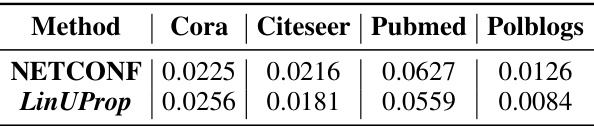
This table compares the runtime performance of NETCONF and LinUProp on four different datasets. The runtime is measured in seconds and includes the computation time for all edges in the graph. The results show that the runtime of both methods is quite similar, though LinUProp shows a minor performance advantage in this specific experimental condition.
Full paper#