A Combinatorial Algorithm for the Semi-Discrete Optimal Transport Problem

↗ OpenReview ↗ NeurIPS Homepage ↗ Chat

TL;DR

#

Key Takeaways

#

Why does it matter?

#

This paper is crucial for researchers working on optimal transport problems because it significantly improves the efficiency of computing optimal transport plans, especially in semi-discrete settings. This opens doors for applying OT to larger datasets and higher dimensions, which are currently computationally expensive. Its combinatorial approach offers an alternative to numerical methods, addressing limitations like smoothness assumptions and slow convergence. The resulting data structure enables faster query responses for large datasets, boosting applications in machine learning and other fields.

Visual Insights

#

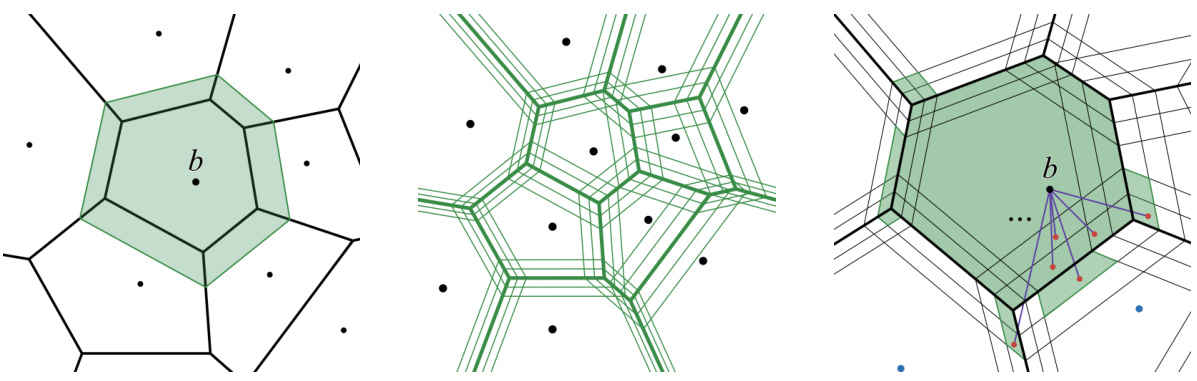
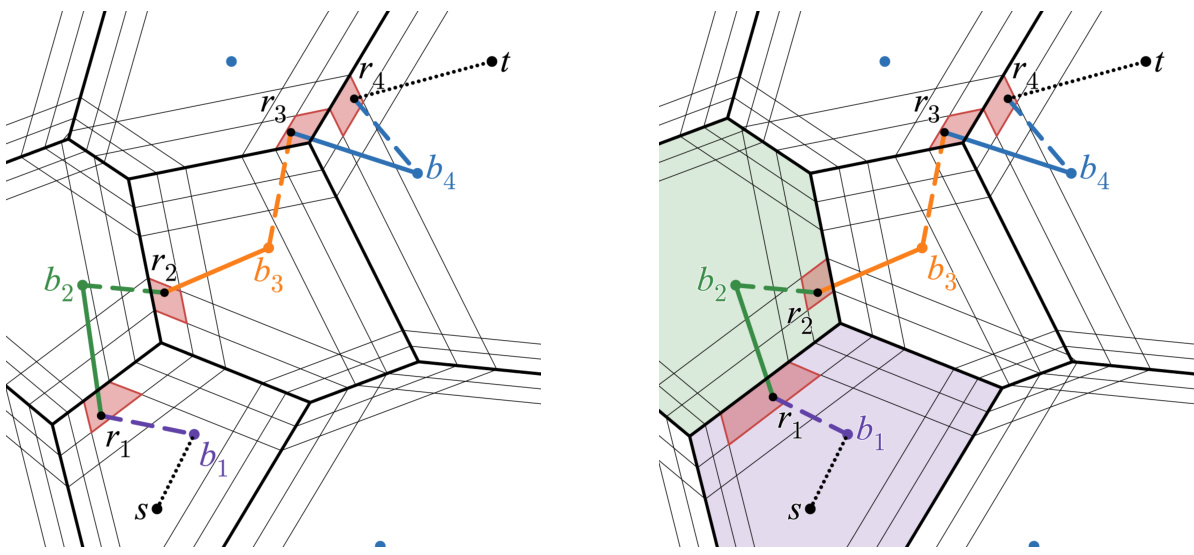
This figure shows three different aspects of the algorithm’s process of transporting mass from a continuous distribution μ to a discrete distribution v. The left panel illustrates the δ-expanded Voronoi cell around a point b, which is a key concept in the optimal transport problem. The middle panel depicts the partitioning of the continuous space into regions based on distances from points in the discrete distribution. The right panel visualizes the compression of the transport plan, showing how mass is moved from a point b to representative points within its Voronoi cell. The color-coding helps in distinguishing the different elements and their relationships in the overall transport plan.

In-depth insights

#

Semi-Discrete OT

#

Semi-discrete optimal transport (OT) presents a compelling blend of continuous and discrete probability distributions. It addresses the challenge of efficiently transporting mass from a continuous source distribution (like an image or a probability density function) to a discrete target distribution (e.g., a set of points representing landmarks or data clusters). This setting is particularly relevant in machine learning applications where data might be represented compactly using continuous models but needs to be compared or aligned with discrete data points. The core difficulty lies in the computational cost: while discrete OT has efficient combinatorial algorithms, directly extending them to the continuous case is computationally intractable. The semi-discrete approach provides a powerful compromise, leveraging both the expressiveness of continuous models and the computational efficiency achievable via discrete methods. The existing methods for tackling semi-discrete OT often involve numerical approximations or rely on assumptions about the smoothness of the source distribution, limiting their generality and efficiency. The combinatorial algorithm described in this paper aims to resolve these limitations by extending the combinatorial framework of discrete OT to the semi-discrete setting. This offers the potential for significantly faster and more robust solutions compared to the existing numerical methods.

Combinatorial Algo

#

A combinatorial algorithm for optimal transport, particularly focusing on the semi-discrete case, presents a novel approach to a computationally challenging problem. The core idea leverages the efficiency of combinatorial methods traditionally applied to discrete optimal transport and extends them to handle continuous distributions. This extension is non-trivial, requiring new techniques to manage the complexities introduced by continuous probability measures. The algorithm’s efficiency stems from cleverly structuring the problem to maintain a tractable size of the computational graph, which would otherwise explode in size. The use of a cost-scaling approach is crucial, breaking down the problem into smaller, manageable subproblems. Furthermore, the algorithm appears to be significantly faster than existing numerical methods, particularly for non-smooth distributions, a known weakness of competing approaches. The algorithm’s design, built upon a primal-dual framework, exhibits elegance and efficiency through careful management of data structures and the introduction of novel concepts like ‘admissible paths’ to streamline the computation. Its scalability, evidenced by the extension to higher dimensions and the development of data structures for efficient querying, further emphasizes its practical significance.

Cost-Scaling Approach

#

A cost-scaling approach is a powerful algorithmic technique for solving optimization problems, particularly those involving combinatorial structures or large-scale datasets. The core idea is to iteratively solve a sequence of progressively refined subproblems, where the cost function is scaled at each iteration. This scaling typically involves multiplying the cost function by a constant factor. Starting with a coarse approximation, the algorithm gradually refines the solution by incorporating more detailed cost information. This iterative refinement process offers several advantages. First, it can dramatically reduce the computational complexity compared to directly solving the original problem. Second, it facilitates the design of efficient approximation algorithms, which are crucial for large-scale instances or problems with intricate structures. Third, it allows for parallelization and distributed computing, as the subproblems can often be solved independently. However, cost-scaling approaches require careful design of the scaling factor and efficient solution methods for the subproblems. The choice of scaling factor can impact both the convergence speed and the quality of the approximation. Inadequate scaling might lead to slow convergence or inaccurate results. Furthermore, efficient subproblem solution methods are crucial, especially for large-scale problems.

Data Structure Design

#

Effective data structure design is crucial for efficient Optimal Transport (OT) computations, especially when dealing with large datasets. A well-designed structure can significantly reduce query times for computing transport plans. For large discrete distributions, a hierarchical or tree-based structure like a k-d tree or a range tree could be advantageous for quickly identifying nearby points, thus accelerating the OT algorithm, especially for low-dimensional data. In higher dimensions, more sophisticated structures such as simplex range searching data structures might be necessary to efficiently query the mass within specific regions. The choice of data structure depends on the specific characteristics of the data, including dimensionality and the desired balance between space and time efficiency. Preprocessing the data into a suitable structure can yield substantial computational savings during the OT query phase. However, the design must carefully consider the trade-offs between storage requirements and query time, and it is important to ensure that the chosen structure aligns with the algorithm’s computational needs for optimal performance.

Future Work

#

The ‘Future Work’ section of this research paper presents exciting avenues for extending the combinatorial algorithm for semi-discrete optimal transport. A primary focus should be on extending the algorithm’s efficiency to higher dimensions, as the current approach is computationally expensive for d > 2. Investigating alternative data structures or approximation techniques to improve scalability in higher dimensions is crucial. Another area deserving further research is exploring the algorithm’s performance with different cost functions, moving beyond the squared Euclidean distance to analyze its applicability in diverse scenarios. Investigating theoretical bounds on the algorithm’s approximation error and convergence rates would be valuable. Furthermore, exploring applications in various machine learning tasks, such as generative modeling, domain adaptation, and reinforcement learning, would demonstrate the practical significance of the approach. Finally, empirical evaluation of the algorithm’s performance against existing methods with a focus on runtime and accuracy would provide valuable insights and support its practical usage.

More visual insights

#

More on figures

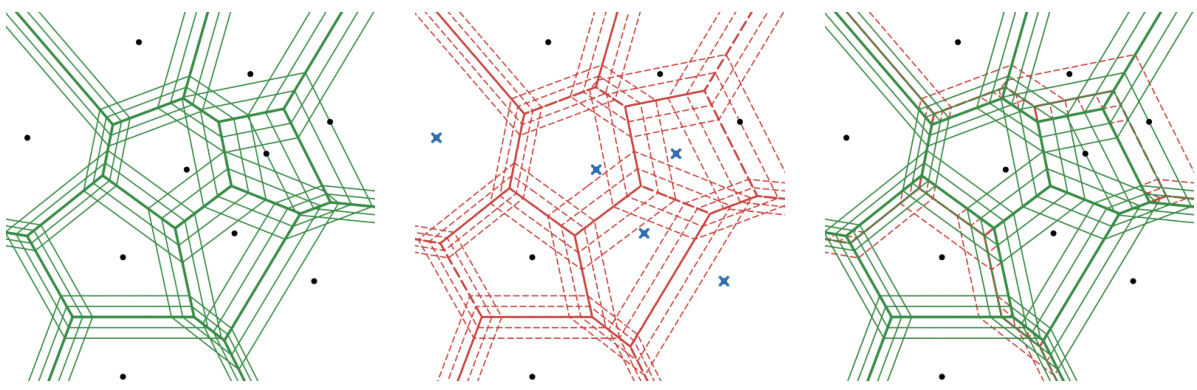
The figure shows three different aspects of the 8-expanded Voronoi cell of point b. (left) shows the 8-expanded Voronoi cell itself. (middle) shows a partitioning of the support set A of the continuous distribution μ into regions, denoted by Xs. (right) shows how mass is transported from point b to regions in Xs. The green region in the right panel represents the mass of μ transported to b, and the red points show the representative points of the regions in Xs. The purple segments represent the compressed transport plan ↑.

The figure illustrates the concept of 8-expanded Voronoi cells in the context of semi-discrete optimal transport. The left panel shows a single 8-expanded Voronoi cell, highlighting its relation to the original Voronoi cell. The middle panel demonstrates the partitioning of the continuous space (A) into regions (Xs) based on the weighted Voronoi diagram. Finally, the right panel showcases how the mass of µ is transported to the discrete points (B) through a compressed transport plan (↑), representing the relationship between the continuous and discrete distributions.

This figure illustrates three key concepts related to the semi-discrete optimal transport problem. The left panel shows an expanded Voronoi cell, highlighting the area from which mass will be transported to point b. The middle panel depicts the partitioning of the continuous distribution’s support into regions (Xs). Finally, the right panel summarizes the compressed transport plan by showing mass transport from point b to the representative points of the relevant regions.

The figure demonstrates the concept of an 8-expanded Voronoi cell and its application in the semi-discrete optimal transport problem. The left panel shows the 8-expanded Voronoi cell of a point ‘b’ from a discrete distribution, highlighting the region where mass from a continuous distribution will be transported to ‘b’. The middle panel shows the partitioning (Xs) of the continuous distribution’s support into regions based on these expanded Voronoi cells. The right panel illustrates a compressed transport plan, where the mass of each region is transported to the point ‘b’ in a simplified representation. This compressed plan makes the algorithm efficient.

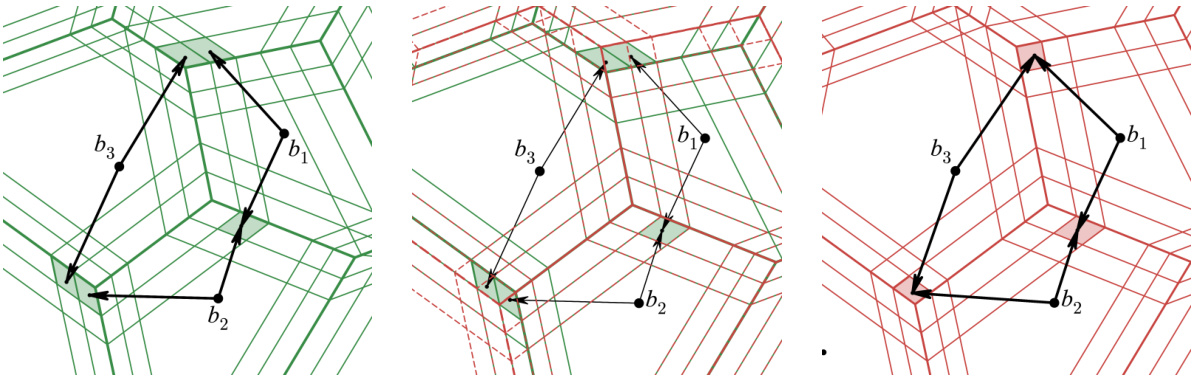
The figure shows three parts. The left part shows an 8-expanded Voronoi cell of point b. The middle part shows the partitioning of the support of the continuous distribution μ into regions. The right part shows the mass of μ that is transported to b, represented by the green region, and the compressed transport plan is represented by purple segments.

The figure shows three different stages of the algorithm. In (a), the 8-expanded Voronoi cell of a point b is highlighted. The middle image (b) shows the partitioning of the continuous support A of the distribution µ into regions. Finally, in (c), the mass transportation plan is represented, where the green regions show the mass of µ transported to b, red points are the representative points for each region, and purple lines represent the transport plan.

This figure shows the process of compressing the semi-discrete transport plan. (Left) shows the 8-expanded Voronoi cell, which is the Voronoi cell considering the weights with an additional parameter. (Middle) shows the partitioning of the continuous distribution’s support based on the 8-expanded Voronoi cells of the discrete distribution’s points. (Right) shows a compressed transport plan where the mass of the discrete distribution is transported to representative points within each partition of the continuous distribution.

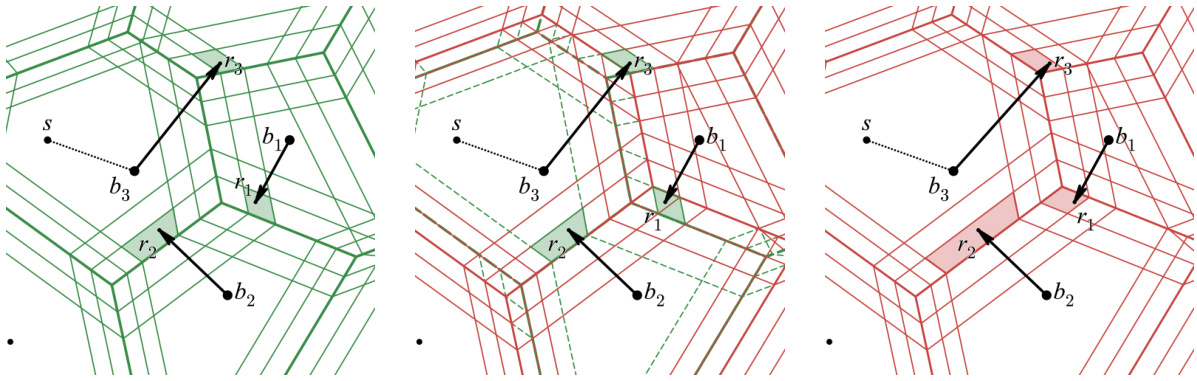
This figure shows three different aspects of the 8-expanded Voronoi cell, which is a core concept used in the combinatorial framework for solving the semi-discrete optimal transport problem. (Left) shows the 8-expanded Voronoi cell of point b, which is the region around b that contains all points closer to b than to any other point in B after adjusting weights by 8. (Middle) illustrates the partitioning of the continuous distribution’s support A created by the arrangement of Voronoi cells and their 8- and 28-expansions. (Right) displays how the continuous mass of the distribution µ inside each region of this partitioning is transported to the corresponding point b in the discrete distribution, represented by the compressed transport plan.

Full paper

#