↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many computational imaging tasks involve solving inverse problems, where the goal is to reconstruct an image from noisy and incomplete measurements. Traditional methods often rely on simple image priors, limiting their ability to reconstruct complex images accurately. Recent advancements in diffusion models have shown their potential in generating realistic images, suggesting that they could improve image reconstruction in inverse problems. However, previous attempts to use diffusion models in this context have relied on approximations that can lead to inaccuracies.
This research introduces a novel method, Plug-and-Play Diffusion Models (PnP-DM), that uses diffusion models as image priors within a Bayesian framework. The key innovation is an algorithm that reduces the problem to a simpler Gaussian denoising problem which is then solved using a general formulation that encompasses a variety of state-of-the-art diffusion models. The results show that PnP-DM significantly improves the accuracy and fidelity of image reconstructions compared to existing methods, especially in challenging problems like black hole imaging.
Key Takeaways#
Why does it matter?#
This paper is crucial for researchers in computational imaging and related fields. It presents a novel, principled Bayesian framework for integrating powerful diffusion models (DMs) as priors in posterior sampling, addressing limitations of existing DM-based methods. This work opens new avenues for solving ill-posed inverse problems accurately, particularly relevant to areas like black hole imaging, and offers insights into non-asymptotic behavior of DM-based MCMC methods.
Visual Insights#

This figure demonstrates the effectiveness of the proposed PnP-DM method on a real-world black hole imaging problem. It shows how the method integrates real-world interferometry measurements with a diffusion model prior to generate accurate posterior samples of the M87 black hole image. The results highlight the method’s ability to capture key features of the black hole, such as its bright spot and ring diameter, despite the challenging nature of the inverse problem.
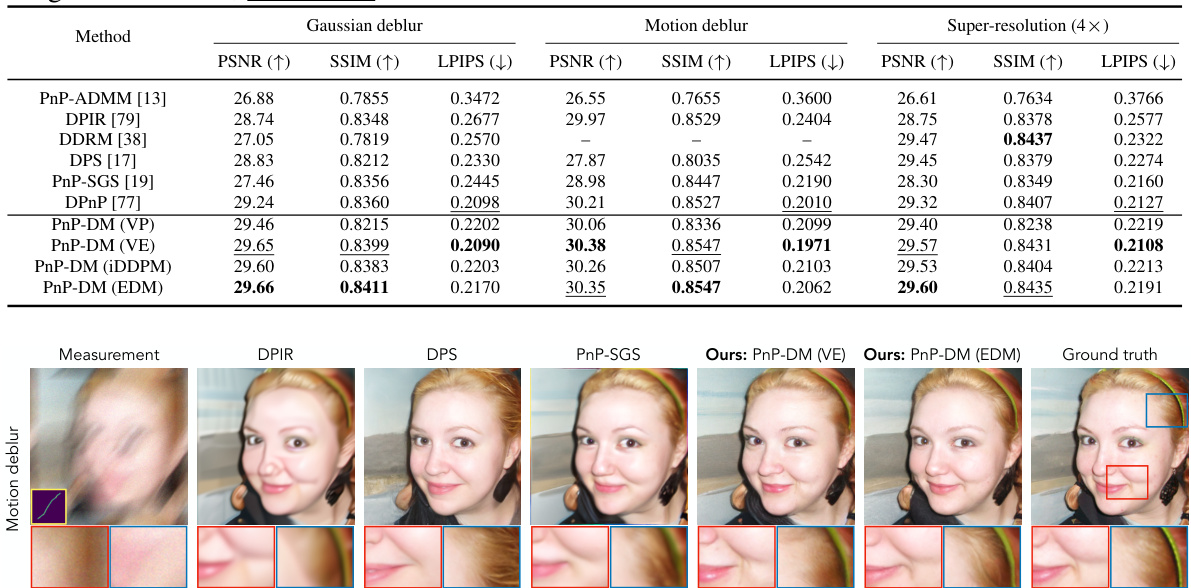
This table presents a quantitative comparison of different methods on three common linear inverse problems: Gaussian deblurring, motion deblurring, and super-resolution. The methods compared include several state-of-the-art approaches and the proposed PnP-DM method using different diffusion models. The performance is evaluated using three metrics: PSNR, SSIM, and LPIPS. The table highlights the superior performance of PnP-DM across all three tasks.
In-depth insights#
PnP-DM: A New MCMC#
PnP-DM, introduced as a novel Markov Chain Monte Carlo (MCMC) method, presents a principled approach to posterior sampling in Bayesian inverse problems. Leveraging diffusion models (DMs) as priors, it avoids the common approximations found in existing DM-based methods, leading to more accurate posterior estimations. The core innovation lies in its rigorous integration of DMs, using the EDM framework as a unified interface, thereby avoiding approximations in the generative process. This allows PnP-DM to handle a wide array of DMs, making it adaptable to various inverse problems. The method’s effectiveness is demonstrated across diverse linear and non-linear problems, including a real-world black hole imaging application, showcasing its superior performance and robustness compared to existing techniques. While it presents a significant step forward, future work could explore handling large-scale inverse problems efficiently, possibly through parallelization or stochastic approximations, and further refine theoretical analysis to account for score function approximation errors.
EDM Prior Integration#
The proposed method’s core innovation lies in its principled integration of diffusion models (DMs) as image priors within a Bayesian framework. Instead of relying on approximations that compromise accuracy, the authors introduce an elegant solution using the Energy-based Diffusion Model (EDM) formulation. EDM provides a unified interface to leverage various state-of-the-art DMs, avoiding the approximations seen in existing methods. This rigorous approach allows for accurate posterior sampling by reducing the inverse problem to a Gaussian denoising problem, where the EDM’s generative power is harnessed. The EDM’s ability to unify diverse DM architectures is crucial, as it offers flexibility and scalability across various imaging tasks. This innovative method contributes significantly to accurate posterior estimation compared to existing techniques, showcasing its potential in tackling complex inverse problems.
Nonlinear Problem Solving#
The paper tackles nonlinear inverse problems by leveraging the power of diffusion models (DMs) within a principled Bayesian framework. A key innovation is the proposed Plug-and-Play Diffusion Model (PnP-DM), a novel Markov Chain Monte Carlo algorithm that avoids common approximations in existing DM-based methods. This approach rigorously integrates DMs as priors, enabling accurate posterior sampling for complex, nonlinear imaging tasks. The method’s effectiveness is demonstrated on challenging real-world problems including black hole imaging, showing superior performance over existing methods in terms of reconstruction accuracy and posterior estimation. While the method demonstrates strong empirical results, limitations include the computational cost for large-scale problems and the reliance on accurate score function estimation. Future work will focus on addressing these limitations to further enhance scalability and robustness. The theoretical analysis partially addresses the non-asymptotic behavior, but a more comprehensive theoretical understanding of the algorithm’s convergence properties is needed.
Non-Asymptotic Analysis#
A non-asymptotic analysis focuses on the finite-time behavior of an algorithm or process, unlike asymptotic analysis which examines the behavior as time goes to infinity. In the context of probabilistic imaging using diffusion models, a non-asymptotic analysis would provide concrete bounds on the error or distance between the algorithm’s output and the true posterior distribution for a fixed number of iterations. This would be crucial for practical applications because it would allow us to determine how many iterations are required to achieve a desired level of accuracy. Key quantities in such analysis might include the Kullback-Leibler (KL) divergence and the Fisher information between the estimated posterior and the true posterior. The analysis might involve establishing a rate of convergence, showing how quickly the error decreases as the number of iterations increases. It would need to account for any approximations or empirical estimations done in the algorithm’s steps, especially those involving score functions approximated via neural networks. Establishing a stationary guarantee would be a significant finding, showing that the algorithm eventually settles to a stable solution, which is especially important for sampling-based approaches.
Black Hole Imaging#
The research demonstrates a novel approach to black hole imaging using diffusion models. It overcomes limitations of existing methods by rigorously integrating diffusion models as priors within a Bayesian framework, avoiding approximations in the generative process. This is achieved through a Markov chain Monte Carlo algorithm that reduces the problem to posterior sampling of a Gaussian denoising problem, efficiently solvable using the proposed method. The approach is validated on real-world data from the Event Horizon Telescope (EHT) observations of the M87 black hole, achieving high-quality reconstructions and demonstrating the method’s robustness and accuracy in posterior estimation compared to existing DM-based methods. A key strength is the use of a unified DM interface, allowing seamless integration of various state-of-the-art diffusion models. The results highlight the power of principled probabilistic methods for tackling complex inverse problems like black hole imaging, showcasing superior accuracy and robustness.
More visual insights#
More on figures
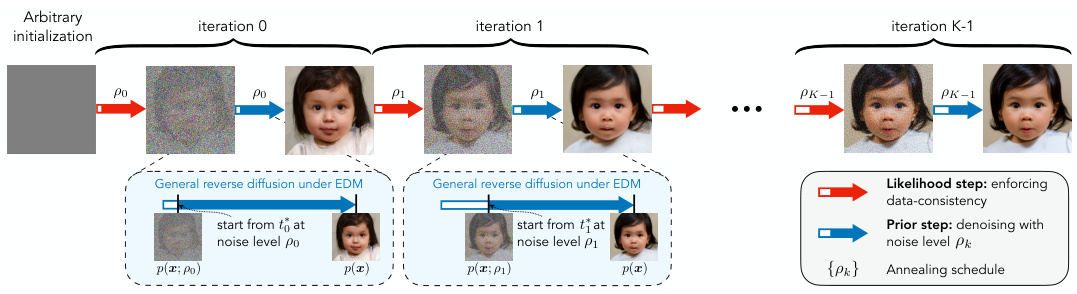
This figure illustrates the workflow of the proposed Plug-and-Play Diffusion Models (PnP-DM) method. It shows how the algorithm alternates between a likelihood step (red) that enforces data consistency and a prior step (blue) that solves a Bayesian denoising problem using diffusion models. The key innovation is the connection to the EDM framework, which enables the use of various state-of-the-art diffusion models as priors for posterior sampling. An annealing schedule (pk) gradually reduces the coupling between likelihood and prior steps to improve efficiency and accuracy.

This figure conceptually illustrates the non-stationary and stationary processes as interpolations of K discrete iterations of the Plug-and-Play Diffusion Models (PnP-DM) algorithm. The non-stationary process starts from an arbitrary initialization (v0) and transitions through K iterations, alternating between likelihood and prior steps. The likelihood step enforces data consistency, while the prior step involves a denoising problem solved using a diffusion model. The prior step incorporates an approximation error. The stationary process starts from a stationary distribution (πΧ) and alternates between stationary distributions (πΧ) and (πZ) during the prior and likelihood steps, respectively. The figure visually shows how the continuous-time processes connect the discrete iterations of PnP-DM. It is a simplified visualization, and the actual processes involve more sophisticated mathematics.

This figure compares the proposed method (PnP-DM) with DPS [17] on a synthetic compressed sensing problem where the ground truth posterior is available. The top row shows the ground truth image, the mean of the ground truth posterior distribution, the mean of the posterior distribution estimated by DPS [17], and the mean of the posterior distribution estimated by PnP-DM. The bottom row shows the standard deviation of the ground truth posterior distribution, the standard deviation estimated by DPS [17], and the standard deviation estimated by PnP-DM. The results demonstrate that PnP-DM more accurately estimates both the mean and standard deviation of the posterior distribution compared to DPS [17].

This figure compares the uncertainty quantification results of different methods for motion deblurring. The left three columns visually represent the absolute error, standard deviation, and z-score of the reconstructions. Outlier pixels are highlighted in red. The rightmost column shows a scatter plot of the absolute error against the standard deviation, clearly illustrating that PnP-DM offers a more accurate uncertainty quantification with fewer outliers and less overestimation of standard deviations, compared to other methods.
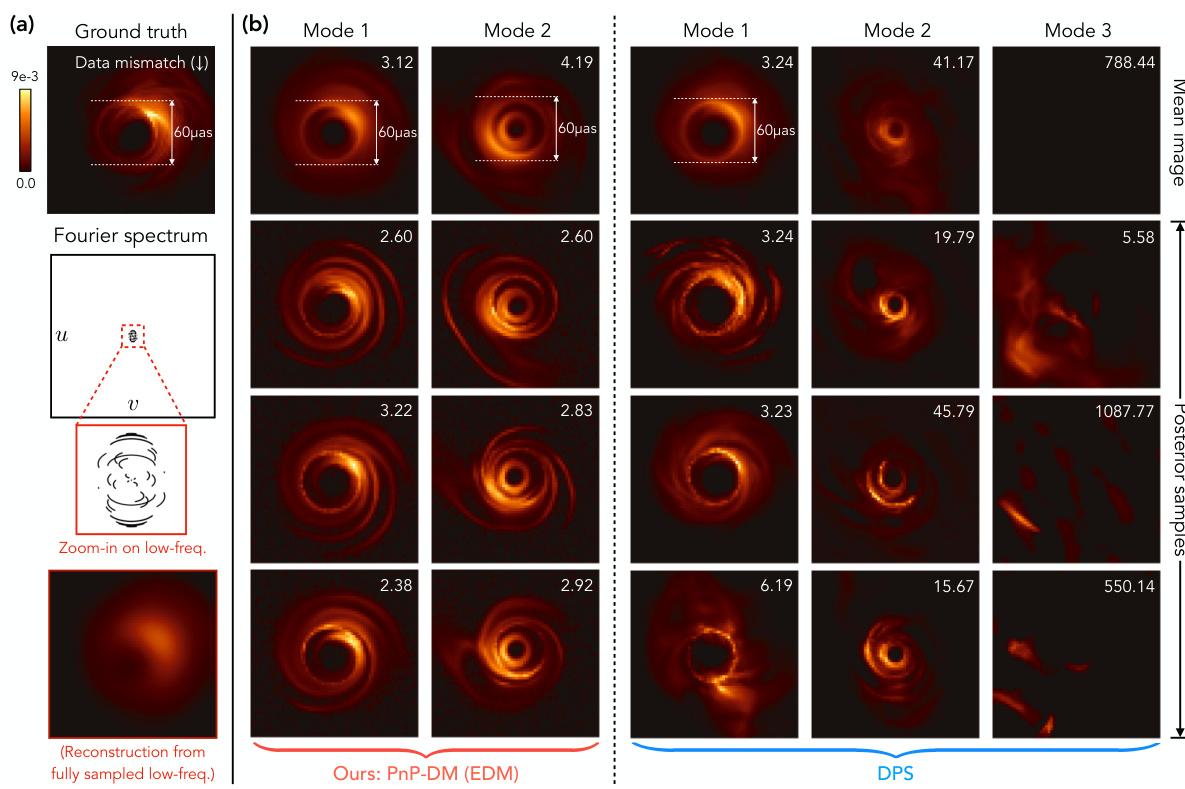
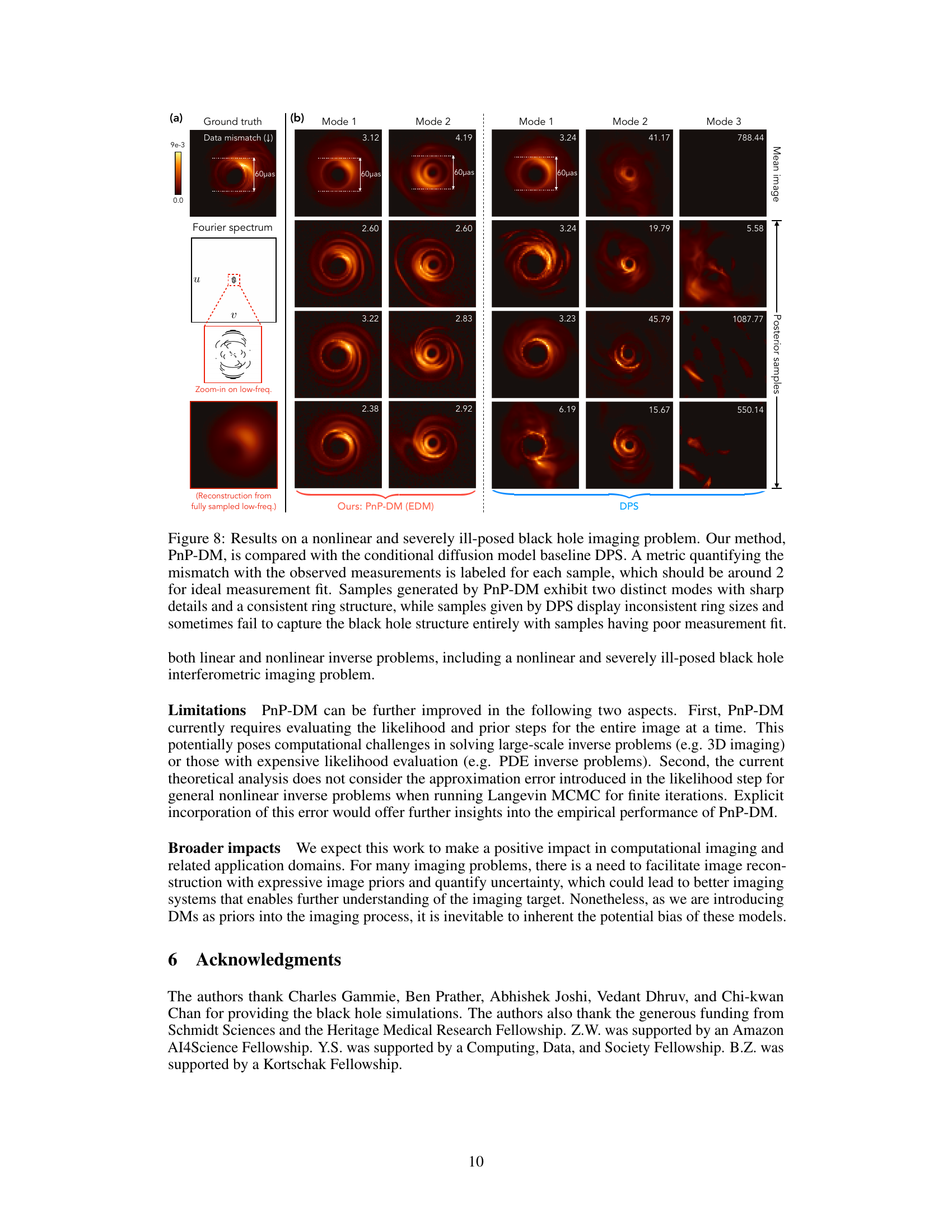
This figure compares the results of PnP-DM and DPS on a black hole imaging problem using simulated data. The left side shows the ground truth image, alongside two modes of posterior samples generated by PnP-DM, with data mismatch values indicating how well each sample fits the observations. The right side displays the results for DPS, showing three modes of posterior samples. The results show PnP-DM’s superior ability to accurately capture the black hole’s key features, such as the ring structure, even in this challenging, ill-posed setting. DPS results exhibit inconsistent ring sizes and often fail to represent the image structure.

This figure demonstrates the application of the proposed PnP-DM method to real-world black hole imaging data. It showcases how the method integrates real-world measurements with a diffusion model prior to generate posterior samples of the black hole image. The results highlight the accuracy and high visual quality of the generated samples, emphasizing their ability to capture important features such as the bright spot and ring diameter.

This figure compares the performance of PnP-DM and DPS [17] methods on a synthetic compressed sensing problem where the ground truth posterior distribution is available. The top row shows the ground truth image, ground truth posterior mean, and posterior samples generated by DPS and PnP-DM. The bottom row shows the ground truth prior mean, ground truth prior standard deviation and the standard deviation of samples generated by DPS and PnP-DM. This visualization demonstrates that PnP-DM more accurately estimates the posterior distribution compared to the DPS method, particularly in terms of standard deviation.

This figure shows a visual comparison of different sampling algorithms on the motion deblurring problem with added Gaussian noise of standard deviation 0.05. The algorithms compared include PnP-ADMM, DPIR, DDRM, DPS, PnP-SGS, DPnP and the proposed PnP-DM using VP and EDM models. Each column displays one sample reconstruction generated by a given algorithm, illustrating the visual differences in reconstruction quality achieved by each method. The results visually demonstrate that the PnP-DM method produces reconstructions of higher quality compared to the baselines.

This figure compares visual results of different algorithms on a motion deblurring task. The input is a blurry image (Measurement), and the outputs are reconstructions by PnP-ADMM, DPIR, DDRM, DPS, PnP-SGS, DPnP, and PnP-DM (with two variants). The ground truth is also shown for comparison. Each algorithm produces a single sample, showcasing their ability to reconstruct a sharp and clear image from blurry input.

This figure shows visual results for motion deblurring with different sampling algorithms. It compares the results of PnP-ADMM, DPIR, DDRM, DPS, PnP-SGS, DPnP, and PnP-DM (with VP and EDM variants). The input blurry images are shown in the first column. Subsequent columns show the reconstructions obtained from each sampling method. The ground truth images are in the final column. This visual comparison highlights the differences in reconstruction quality among the different methods.

This figure demonstrates the effectiveness of PnP-DM on a real-world black hole imaging problem. It shows how the method integrates real-world interferometry measurements with a diffusion model prior to produce posterior samples of the M87 black hole image. The results highlight the accuracy and visual quality of the method, capturing key features such as the bright spot and ring diameter, in comparison to the official image by the Event Horizon Telescope (EHT).

This figure displays visual results for motion deblurring with different algorithms. The input is a blurred image, and each column shows the reconstruction obtained with different methods (PnP-ADMM, DPIR, DDRM, DPS, PnP-SGS, DPnP, and the three variants of PnP-DM using VP, VE, and iDDPM). It allows for a visual comparison of the quality and detail of the reconstructions produced by each algorithm.

This figure shows the results of a simulated compressed sensing problem using a Gaussian prior. The accuracy of posterior sampling is compared between PnP-DM and DPS methods. The ground truth posterior is available for evaluation. The image shows that PnP-DM can accurately estimate both the mean and standard deviation of the posterior distribution, while DPS deviates significantly from the ground truth.
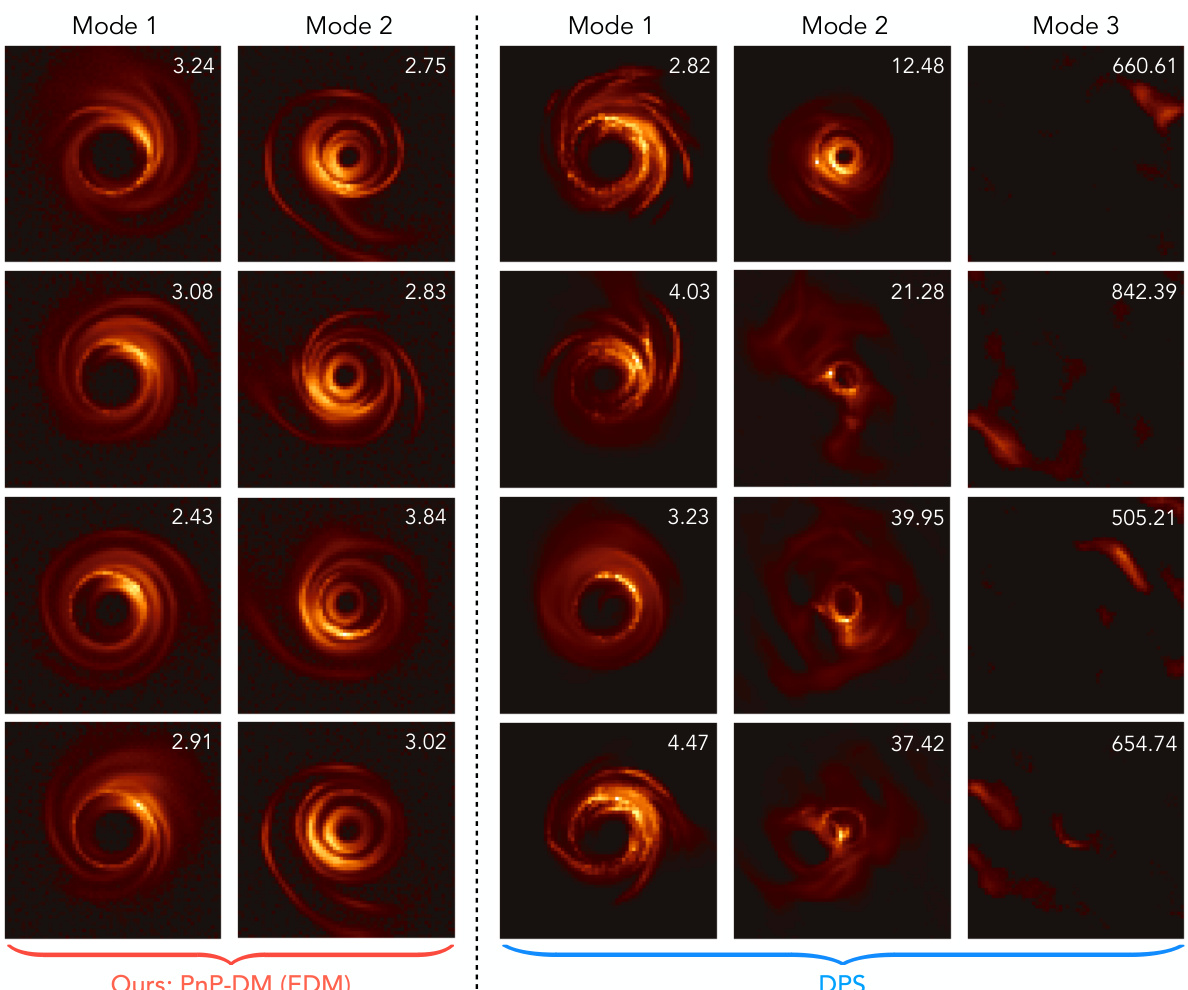
This figure compares the performance of PnP-DM and DPS on a black hole imaging problem. PnP-DM shows two distinct modes with high-quality, detailed reconstructions and consistent ring structure; DPS reconstructions show inconsistent ring sizes and poor fit to measurements in some modes.

This figure demonstrates the proposed method, PnP-DM, applied to real-world black hole imaging data. It highlights the method’s ability to generate high-quality posterior samples that accurately reflect key features of the black hole, such as the bright spot and ring diameter, despite the challenging, ill-posed nature of the inverse problem.
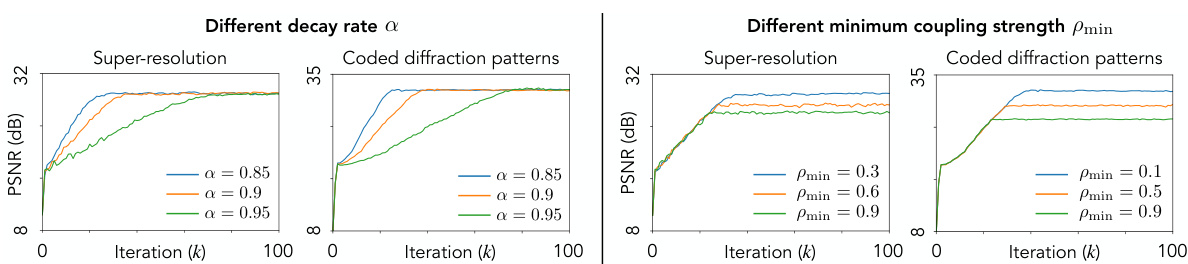
This figure shows a schematic of the Plug-and-Play Diffusion Models (PnP-DM) method. The method iterates between two steps: a likelihood step that enforces data consistency and a prior step that performs posterior sampling for a denoising problem. The prior step leverages the EDM framework and state-of-the-art diffusion models for efficient and accurate sampling. An annealing schedule helps to control the balance between the likelihood and prior steps, improving efficiency and accuracy. The figure highlights the key connection between the Bayesian denoising problem and the unconditional image generation problem of the EDM framework.

This figure shows the intermediate results of the super-resolution experiment. The left panel shows a sequence of intermediate images produced during the iterative process of the proposed algorithm, namely, the xk and zk. The right panel shows the convergence curves of PSNR, SSIM, and LPIPS metrics, demonstrating the algorithm’s ability to approach the ground truth as iterations progress.
More on tables
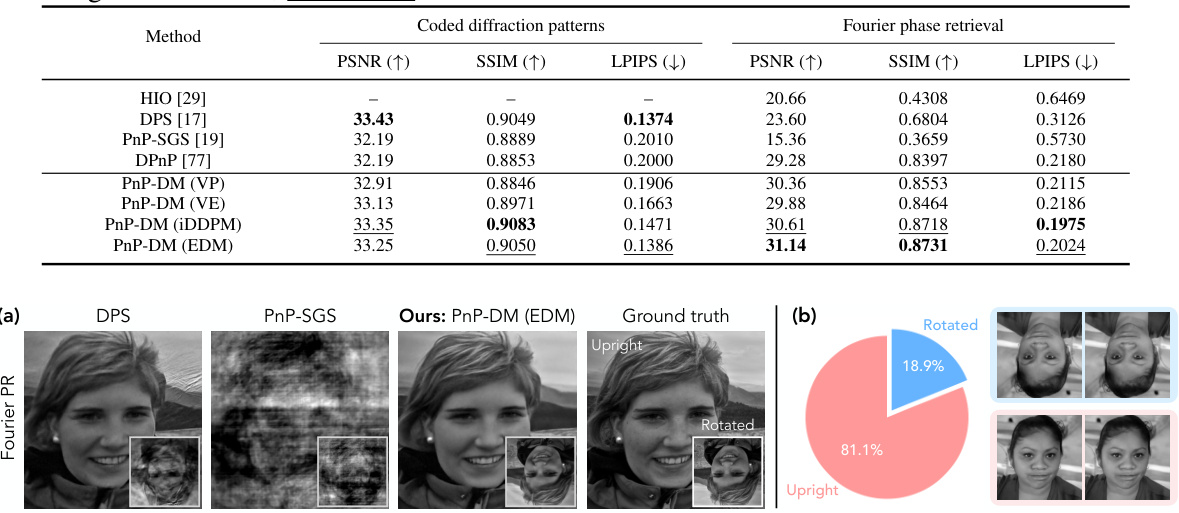
This table presents a quantitative comparison of different methods on two nonlinear inverse problems: coded diffraction patterns and Fourier phase retrieval. The performance is evaluated using PSNR, SSIM, and LPIPS metrics for 100 grayscale images from the FFHQ dataset. The best and second-best results are highlighted in bold and underlined, respectively. This allows for a direct comparison of the proposed PnP-DM method against several baselines.

This table compares the performance of the proposed PnP-DM method against several state-of-the-art baselines on three standard linear inverse problems: Gaussian deblurring, motion deblurring, and super-resolution. The evaluation metrics used are PSNR, SSIM, and LPIPS. The results show that PnP-DM consistently achieves higher PSNR and SSIM scores and lower LPIPS scores, indicating superior image reconstruction quality compared to the baselines.

This table presents a quantitative comparison of different methods on three noisy linear inverse problems using 100 FFHQ color test images. The metrics used for comparison are PSNR, SSIM, and LPIPS. The best performing method for each metric is shown in bold, and the second-best is underlined. The table allows for a comparison of the proposed method (PnP-DM) with several existing state-of-the-art methods.

This table presents a quantitative comparison of the proposed PnP-DM method against several state-of-the-art baselines on three different noisy linear inverse problems. The performance is measured using three metrics: PSNR, SSIM, and LPIPS, for 100 color images from the FFHQ dataset. The best and second-best results for each metric are highlighted in bold and underlined, respectively. The table allows for a detailed comparison of the methods across various aspects of image reconstruction quality.

This table presents a quantitative comparison of the proposed PnP-DM method against several state-of-the-art baselines on three different linear inverse problems: Gaussian deblurring, motion deblurring, and super-resolution. The performance is measured using three metrics: PSNR, SSIM, and LPIPS. The table shows that PnP-DM consistently achieves better or comparable results compared to other methods, highlighting its effectiveness in solving linear inverse problems.
Full paper#