↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Imitation learning (IL) in multi-agent systems faces challenges like high-dimensional spaces and complex inter-agent dependencies. Existing methods often struggle with instability due to adversarial training. Cooperative settings require learning both local value functions for individual actions and a joint value function to exploit centralized learning. This creates a difficult optimization problem.
This paper introduces Multi-agent Inverse Factorized Q-learning (MIFQ), addressing these issues. MIFQ leverages inverse soft Q-learning, avoiding adversarial training. It uses mixing networks for centralized learning, theoretically establishing convexity conditions in the Q-function space. Experiments on challenging benchmarks, including a challenging version of StarCraft, demonstrate MIFQ’s effectiveness and state-of-the-art performance.
Key Takeaways#
Why does it matter?#
This paper is important because it offers a novel solution to a challenging problem in multi-agent imitation learning. It introduces a new algorithm (MIFQ) that overcomes the limitations of existing methods by using factorization and inverse soft Q-learning. This approach leads to more stable and efficient training, opening new avenues for research in cooperative multi-agent systems and other complex domains.
Visual Insights#
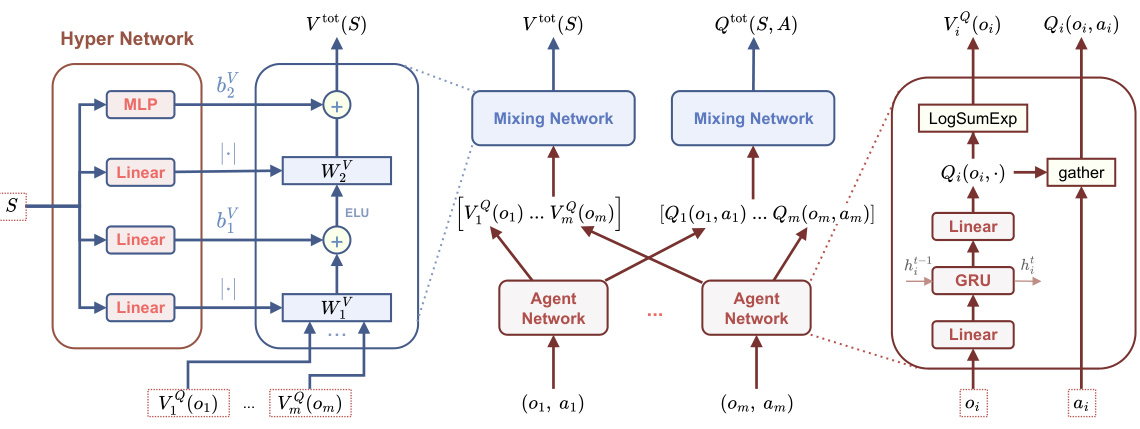
This figure presents a detailed illustration of the multi-agent inverse factorized Q-learning (MIFQ) network architecture. It shows the interplay between three main network components: agent local networks, value mixing networks, and hyper-networks. The agent local networks process individual agent observations and actions to produce local Q-values and V-values. These local values are then aggregated by the mixing networks, which use hyper-network outputs (weights and biases) modulated by the global state. The hyper-networks themselves take the global state as input, providing a dynamic weighting scheme for the mixing networks. The final output represents the joint Q-value and V-value, which contribute to the model’s training objective. The GRU components represent the recurrent neural network used to handle sequential data. The figure visually demonstrates the centralized training with decentralized execution (CTDE) paradigm employed by MIFQ, where global information (from the hyper-network) is used to learn decentralized policies.
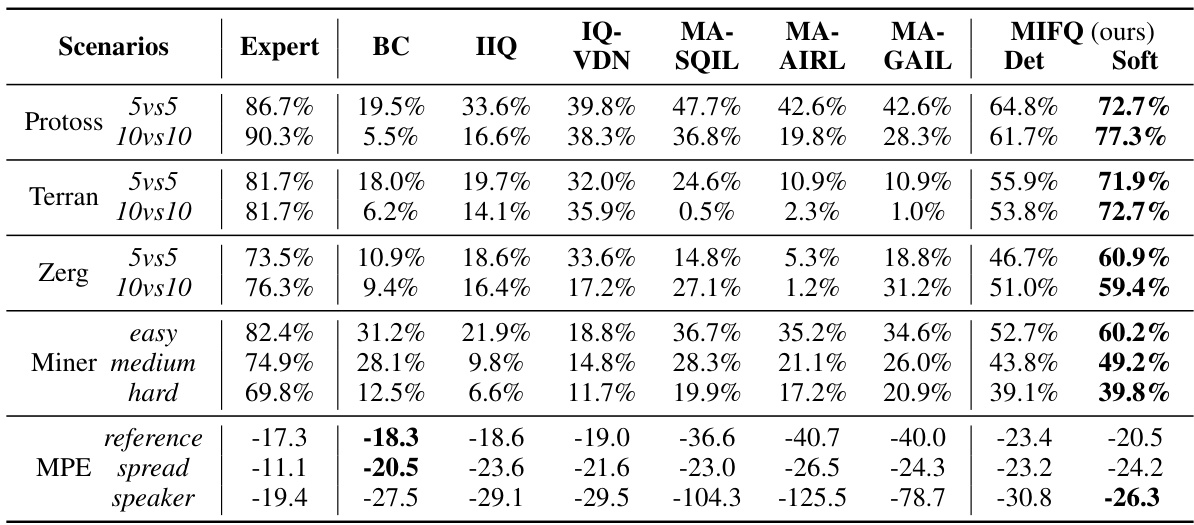
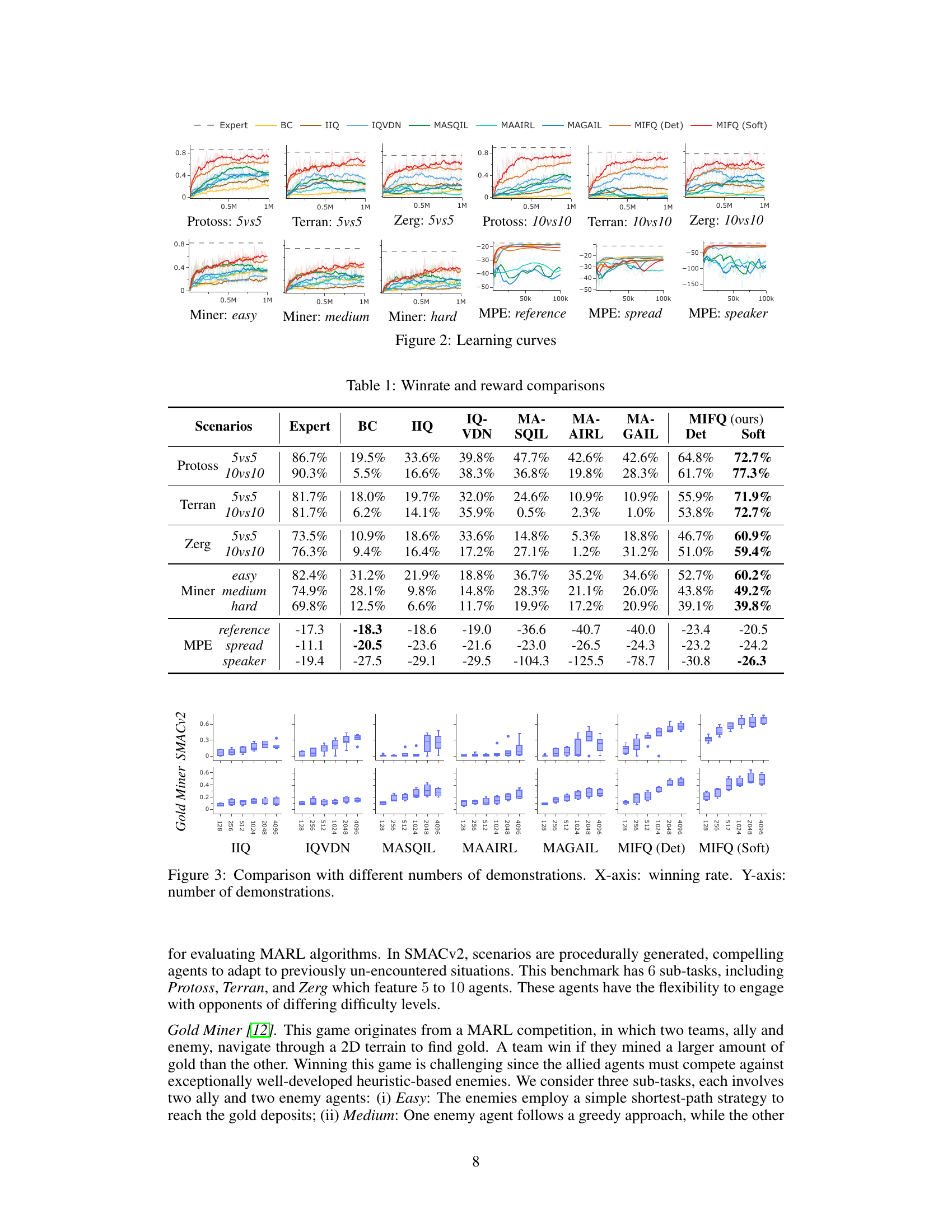
This table presents a comparison of the win rates and rewards achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different game maps and agent numbers in the StarCraft Multi-Agent Challenge (SMACv2), Gold Miner tasks with varying difficulties, and Multi-Particle Environments (MPE) with different configurations. The algorithms compared include Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-learning with Inverse Reinforcement Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm with both deterministic and soft policies. The results demonstrate the superior performance of MIFQ in most scenarios.
In-depth insights#
Inverse Soft Q-Learning#
Inverse Soft Q-Learning offers a compelling approach to imitation learning by framing the problem as a concave maximization rather than a challenging max-min optimization. This reformulation, based on the soft Q-function, elegantly avoids the instability often associated with adversarial methods. The key advantage lies in its ability to learn a single Q-function that implicitly defines both the reward and policy, streamlining the learning process. However, extending this single-agent framework to multi-agent scenarios presents significant challenges, primarily due to the need to handle intricate inter-agent dependencies and high-dimensional state and action spaces. The paper proposes a solution that leverages centralized training with decentralized execution (CTDE) and mixing networks, enabling efficient aggregation of decentralized Q-functions to achieve a centralized learning objective while preserving the advantages of the inverse soft Q-learning framework. This approach further incorporates a generalized version of the Individual-Global-Max (IGM) principle, ensuring consistency between global and local policies. The theoretical analysis demonstrates that under specified conditions (non-negative weights, convex activation functions), the multi-agent objective function remains concave, enhancing training stability. The effectiveness of this approach is validated through experiments on various multi-agent environments, showcasing its superior performance compared to other existing baselines.
Multi-Agent Factorization#
Multi-agent factorization methods address the challenge of scaling multi-agent reinforcement learning (MARL) to large numbers of agents. Traditional MARL approaches often struggle with the exponential growth in state and action space complexity as the number of agents increases. Factorization techniques aim to decompose the joint value function or policy into smaller, more manageable components associated with individual agents or groups of agents. This decomposition significantly reduces the computational burden, allowing for efficient learning and scaling to larger problems. Centralized training with decentralized execution (CTDE) is often employed, where a centralized network learns a global value function based on factorized components, and then decentralized policies are derived from this global estimate. However, different factorization approaches exhibit varying levels of success depending on the specific MARL problem and the nature of the inter-agent dependencies. While some methods, like QMIX, show promise in cooperative settings, others struggle with issues of monotonicity or non-convexity, hindering stable training. Furthermore, the choice of factorization impacts not just the scalability but also the expressiveness of the model. Successfully finding a balance between computational efficiency and the ability to capture complex multi-agent interactions remains an active area of research in MARL.
IGC Principle#
The paper introduces the Individual-Global-Consistency (IGC) principle as a crucial element in its multi-agent inverse soft Q-learning framework. IGC generalizes the existing Individual-Global-Max (IGM) principle, addressing limitations of IGM in the context of soft policy optimization. Unlike IGM, which focuses on the equivalence of optimal joint and individual actions, IGC ensures consistency between the distribution of joint actions from the global optimal policy and the combined distributions of local actions from individual optimal policies. This nuanced approach is critical because the method employs soft policies derived from maximizing entropy, which fundamentally differs from the hard-max actions assumed in IGM. The paper demonstrates that under specific conditions (convex activation functions, non-negative weights in mixing networks), the proposed factorization approach satisfies IGC, resulting in a well-behaved, non-adversarial training objective. This contributes to the stability and effectiveness of the overall multi-agent imitation learning algorithm, showcasing IGC’s importance in tackling the challenges of cooperative multi-agent settings.
Non-Adversarial Training#
The concept of “Non-Adversarial Training” in the context of imitation learning is a significant departure from traditional adversarial methods. Adversarial approaches, like GANs, often suffer from instability and difficulty in training, stemming from the inherent min-max optimization problem. In contrast, non-adversarial training aims to directly optimize a single objective function, typically involving a reward or Q-function, thereby sidestepping the issues of instability and high variance gradient estimates. This approach often involves transforming the original max-min problem, perhaps using a technique like inverse soft Q-learning, into a concave maximization problem that is more amenable to standard optimization techniques. The key benefit lies in the improved stability and efficiency of the learning process, enabling faster convergence and potentially better generalization. However, the effectiveness of non-adversarial methods relies heavily on the appropriate problem formulation and the choice of objective function, and it may not always be possible to transform adversarial objectives into their non-adversarial equivalents.
SMACv2 Experiments#
The SMACv2 experiments section would likely detail the application of the proposed multi-agent inverse factorized Q-learning (MIFQ) algorithm to the challenging StarCraft Multi-Agent Challenge (SMAC) version 2 environment. The authors would present results demonstrating the algorithm’s performance against established baselines. Key aspects to look for include a description of the specific SMACv2 maps used, a comparison of MIFQ’s win rates and reward scores against other methods, and an analysis of the algorithm’s training stability and efficiency. Given the complexity of SMACv2, a detailed discussion of the hyperparameter settings and the experimental setup is expected. The authors might also showcase the algorithm’s ability to generalize across different maps or scenarios, and an examination of the algorithm’s scalability with respect to the number of agents is crucial. Further insights into how the factorization of Q-functions and the utilization of mixing networks contribute to performance in this complex, high-dimensional environment would be particularly valuable. Ultimately, this section serves to validate the effectiveness of MIFQ in a challenging real-world setting and contribute significantly to the field of multi-agent imitation learning.
More visual insights#
More on figures
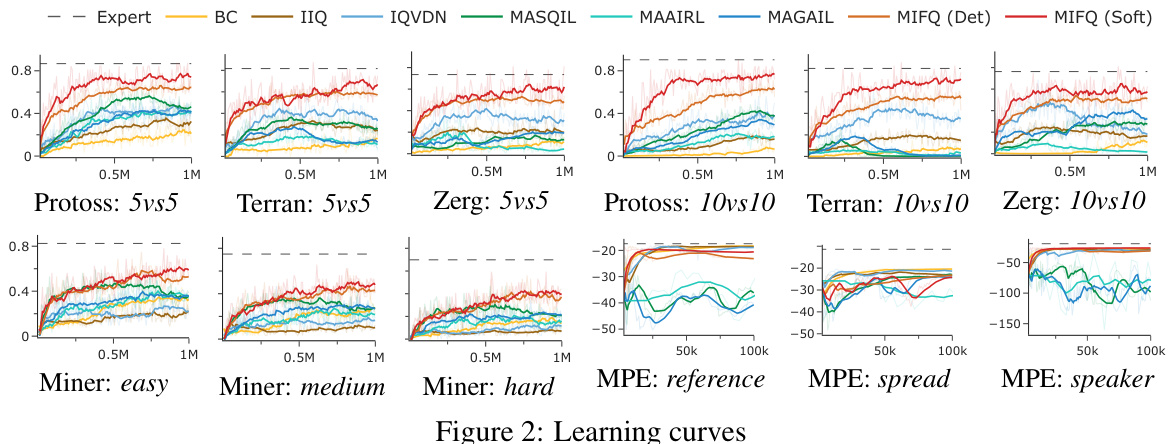
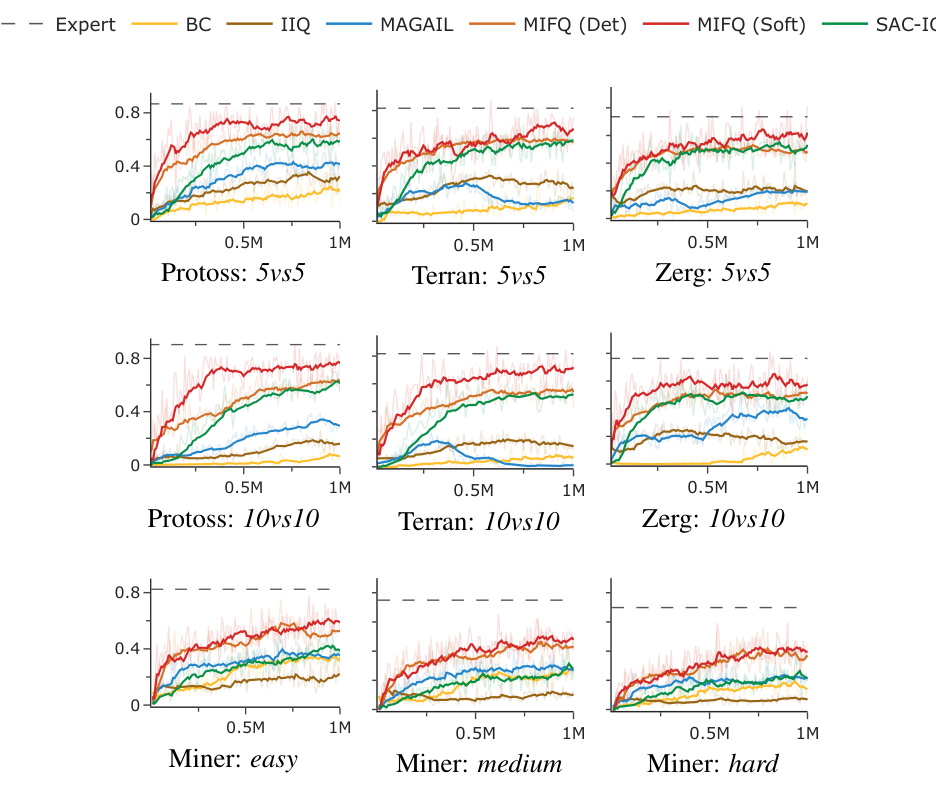
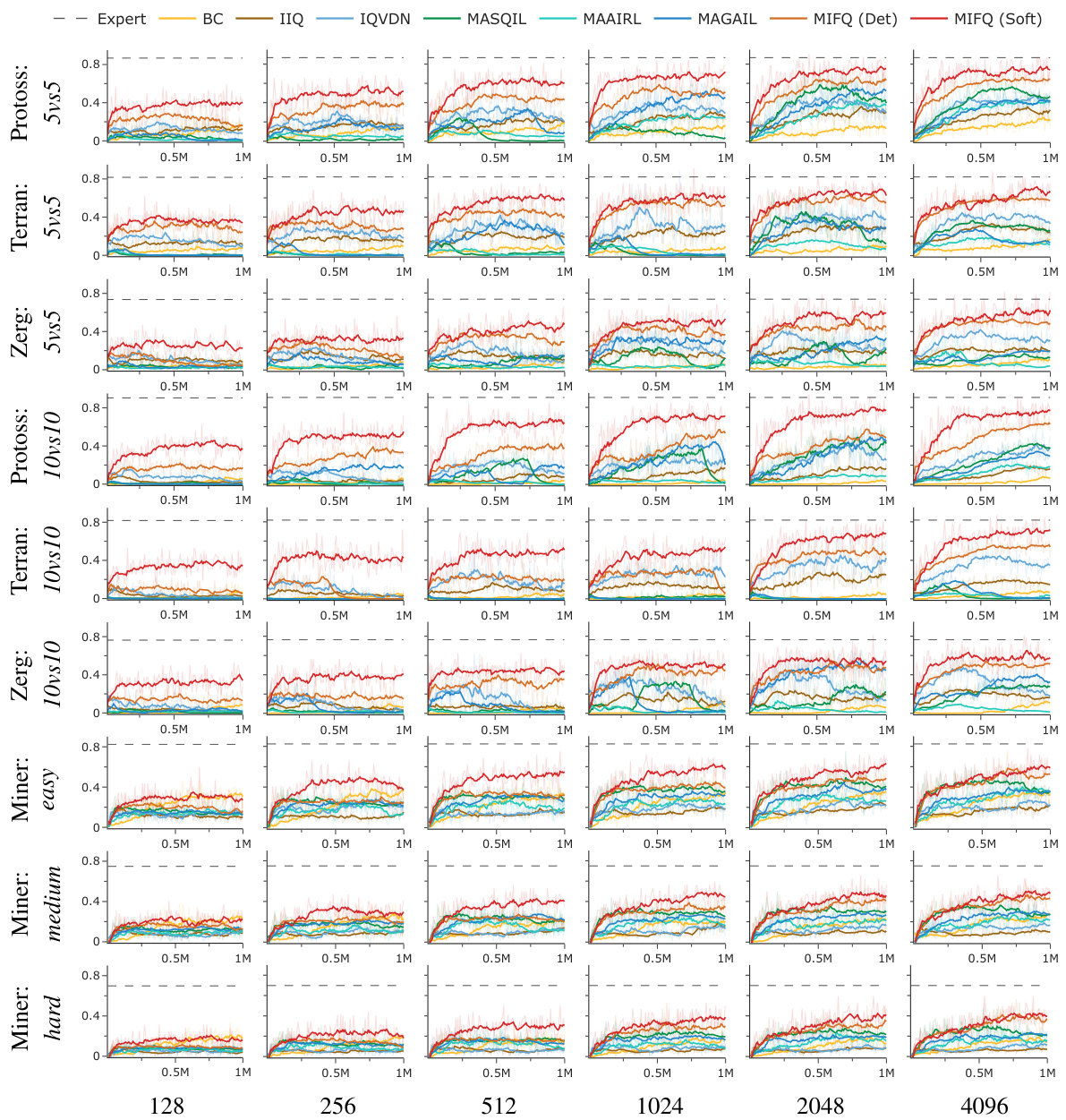
The figure shows learning curves for different multi-agent reinforcement learning algorithms across various tasks. The x-axis represents the training steps, and the y-axis represents the performance metric (winrate or reward), depending on the specific task. The plot visualizes the training progress of each algorithm, allowing for a comparison of their learning efficiency and convergence. Different colored lines indicate different algorithms, and the legend specifies them. Each subplot represents a distinct task, encompassing several scenarios from StarCraft II (SMACv2), Gold Miner, and Multi-Particle Environments (MPE). The figure illustrates the effectiveness of the proposed algorithm (MIFQ) in comparison to other state-of-the-art methods across diverse environments.
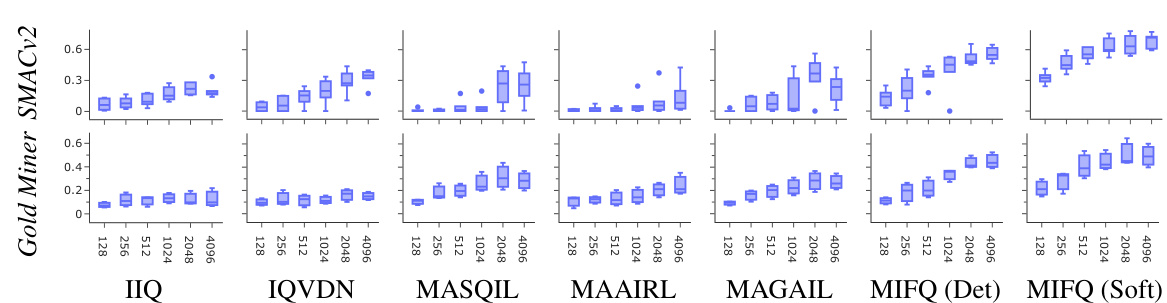
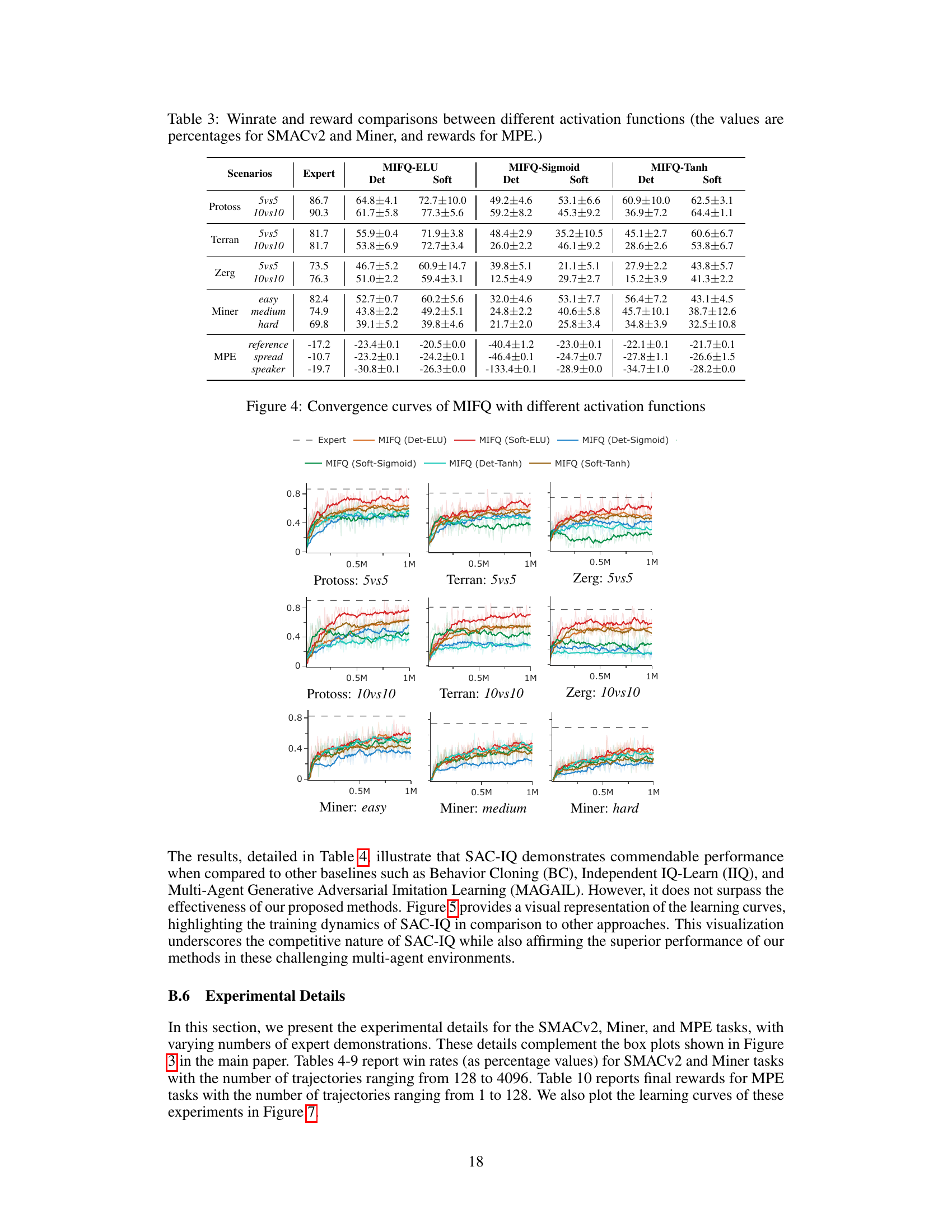
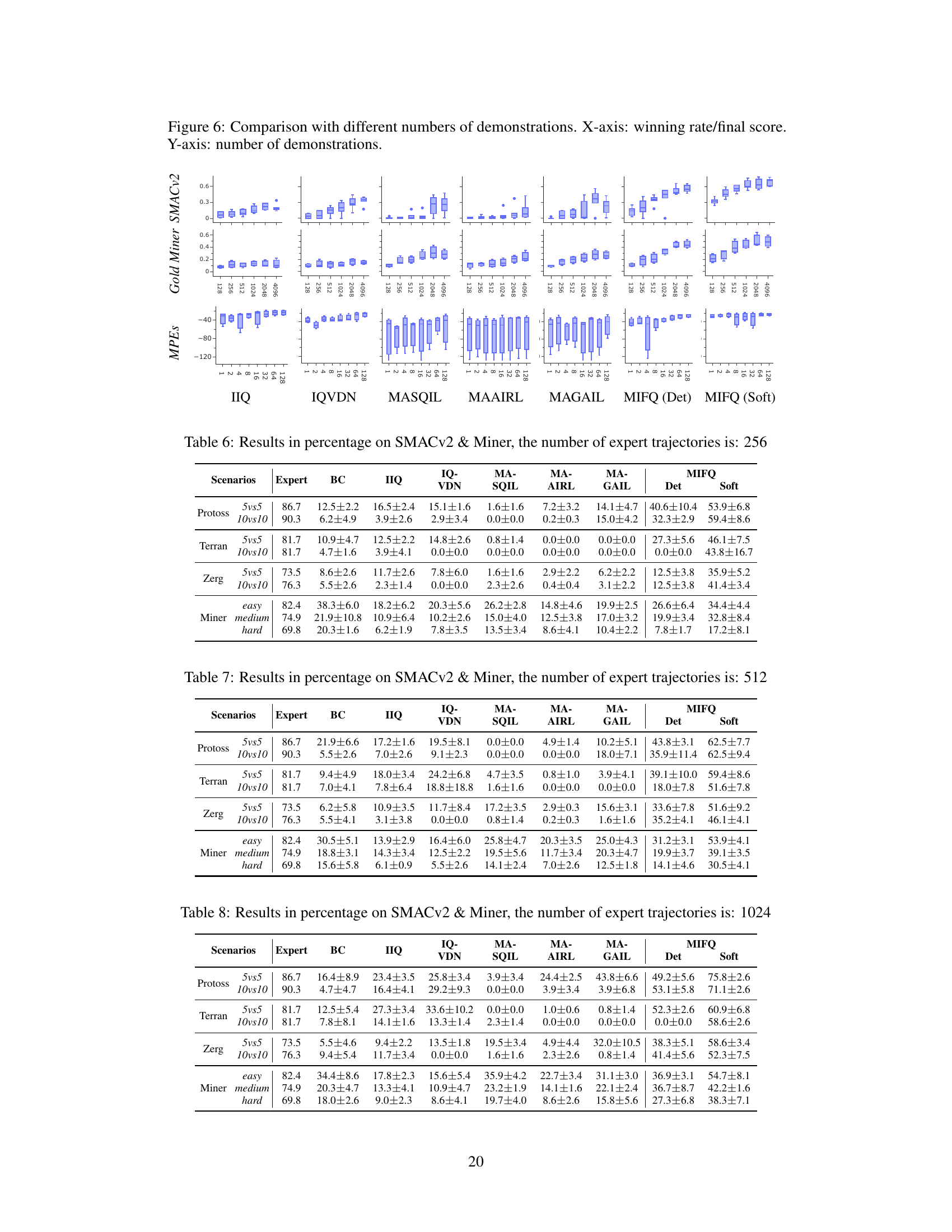
This figure compares the performance of various multi-agent imitation learning algorithms across different numbers of expert demonstrations. The x-axis represents the winning rate achieved by each algorithm, and the y-axis indicates the number of expert demonstrations used for training. The box plots summarize the distribution of winning rates across multiple trials for each algorithm and demonstration count. This visualization helps to assess how the algorithms’ performance scales with the amount of training data available.
This figure presents a detailed illustration of the multi-agent inverse factorized Q-learning (MIFQ) network architecture. It comprises three main components: agent local networks, value mixing networks, and hyper-networks. The agent local networks generate local Q-values and V-values for individual agents based on their observations and actions. These local values are then aggregated into global Q-values and V-values by the value mixing networks. Finally, the hyper-networks determine the weights of the mixing networks dynamically based on the global state. This centralized training with decentralized execution approach allows for the effective integration of individual agents’ learning to solve the multi-agent imitation learning problem.
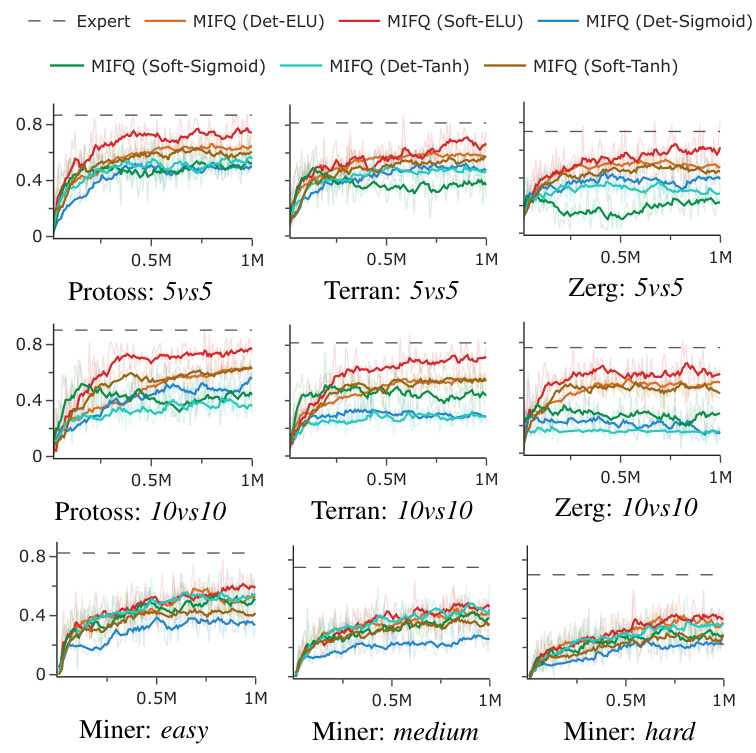
This figure shows the network architecture used in the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm. It details the components, including agent local networks which process local observations and actions, mixing networks combining these to compute global Q and V values, and hyper-networks providing weights to the mixing networks based on the global state. The figure illustrates the flow of information and the interaction between the different network components, emphasizing the centralized training with decentralized execution (CTDE) approach.
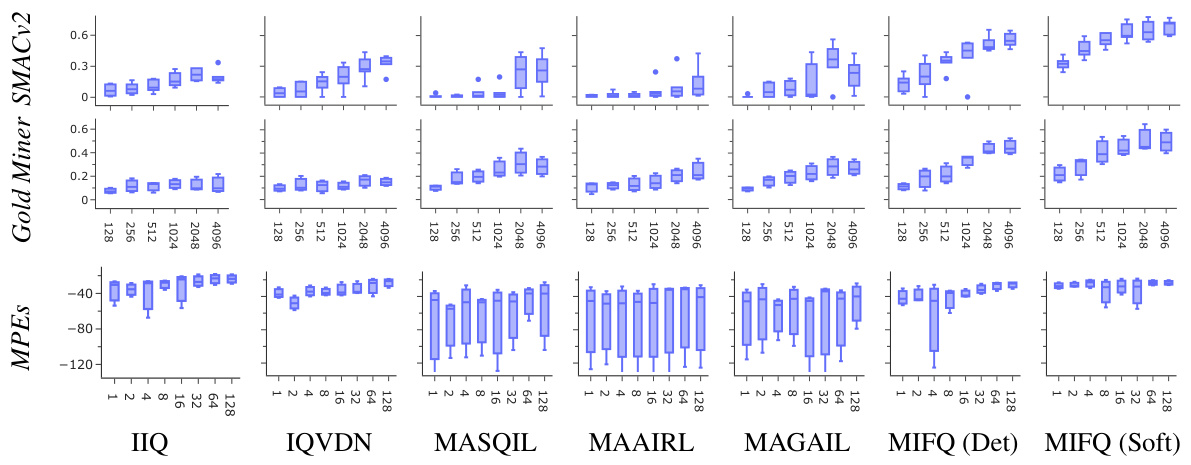
This figure compares the performance of different multi-agent imitation learning algorithms across various tasks (Protoss, Terran, Zerg in SMACv2; easy, medium, hard in Gold Miner) with varying numbers of expert demonstrations (128, 256, 512, 1024, 2048, 4096). The x-axis represents the winning rate achieved by each algorithm, and the y-axis indicates the number of expert demonstrations used for training. The box plots show the distribution of winning rates across multiple runs for each algorithm and number of demonstrations, providing insights into the performance consistency and sensitivity to the amount of expert data.
This figure shows the network architecture used in the Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm. It details the three main components: agent local networks (producing local Q-values), value mixing networks (combining local values into joint values), and hyper-networks (generating weights for the mixing networks based on global state information). The figure illustrates how local Q-values are processed and aggregated to produce global Q-values and the global value function, facilitating centralized training with decentralized execution (CTDE).
More on tables

This table presents a comparison of the win rates and rewards achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different settings of the StarCraft multi-agent challenge (SMACv2) and the Gold Miner game, categorized by the game type (Protoss, Terran, Zerg) and the number of agents (5vs5, 10vs10). The algorithms being compared are Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-Learning with Adversarial Imitation Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm (both deterministic and soft versions). The results show that the proposed MIFQ algorithm generally outperforms the baseline methods.

This table presents the hyperparameters used in the experiments for different environments (MPES, Miner, SMACv2). The hyperparameters include the maximum number of training steps, the evaluation frequency, the buffer size, learning rate, batch size, hidden dimension size, the gamma value, the target update frequency, and the number of random seeds used.

This table presents a comparison of the win rates and rewards achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different settings from StarCraft (Protoss, Terran, Zerg), Gold Miner (easy, medium, hard), and Multi-Particle Environments (reference, spread, speaker). The algorithms compared include Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), Inverse Q-Learning with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-learning with Inverse Reinforcement Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) with deterministic (Det) and soft (Soft) policies.
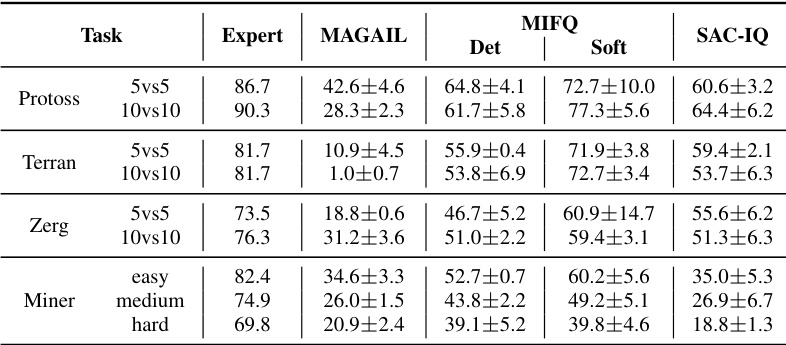
This table presents a comparison of the win rates and reward values achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios are categorized by game (Protoss, Terran, Zerg, and Miner) and difficulty level (5vs5, 10vs10, easy, medium, hard). The algorithms compared are Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), Inverse Q-Learning with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-Learning with Adversarial Inverse Reinforcement Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm (both deterministic and soft versions). The table shows that MIFQ outperforms the baselines in most cases.
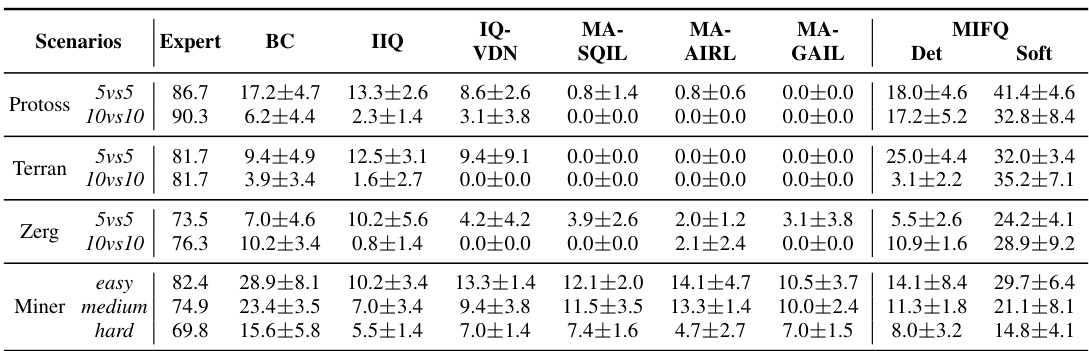
This table presents a comparison of win rates and rewards achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different game settings (Protoss, Terran, Zerg) and difficulty levels (easy, medium, hard) in the StarCraft and Gold Miner games, as well as different MPE scenarios. The algorithms compared are Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-Learning with Implicit Rewards (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm with both deterministic (Det) and soft (Soft) policies. The table highlights the superior performance of the proposed MIFQ algorithm.
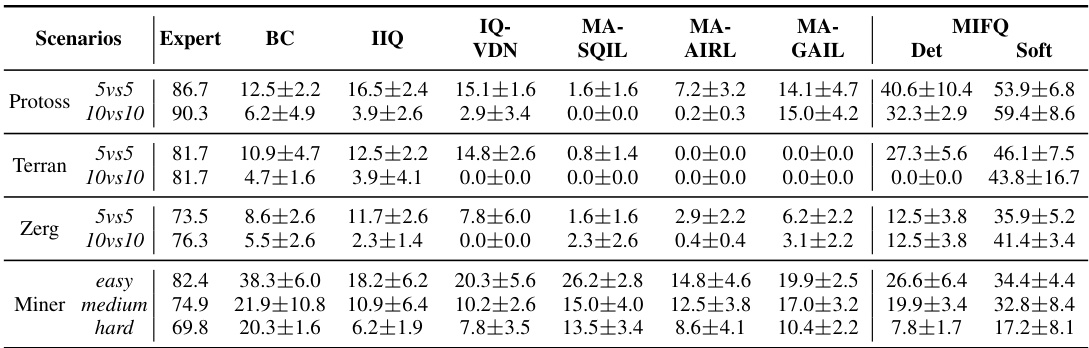
This table presents a comparison of the win rates and rewards achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different game settings (Protoss, Terran, Zerg) with varying numbers of agents (5vs5 and 10vs10), as well as different difficulty levels in the Gold Miner game (easy, medium, hard) and several Multi-Particle Environment (MPE) scenarios (reference, spread, speaker). The algorithms compared are Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-Learning with Adversarial Inverse Reinforcement Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) with both deterministic and soft policy versions.

This table presents a comparison of the win rates and reward values achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different game maps and sizes (5vs5 or 10vs10) for the StarCraft Multi-Agent Challenge (SMACv2), different difficulty levels of the Gold Miner game, and different variations of the Multi-Particle Environment (MPE) game. The algorithms compared include Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-Imitation Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) with deterministic and soft policies. The results show that MIFQ generally outperforms other baselines across various scenarios.
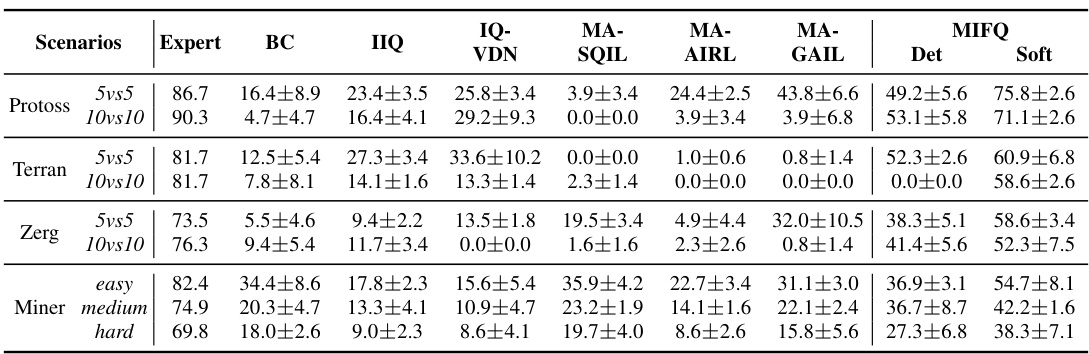
This table presents a comparison of the win rates and rewards achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different combinations of the Protoss, Terran, and Zerg races in the StarCraft multi-agent challenge (SMACv2) environment, as well as different difficulty levels in the Gold Miner game and various configurations of multi-particle environments (MPE). The algorithms compared include Behavior Cloning (BC), Independent IQ-Learn (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), Multi-agent Soft Q-learning with Implicit Reward Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm (both deterministic and soft versions). The expert results are also presented as a benchmark.

This table presents a comparison of the win rates and reward values achieved by different multi-agent imitation learning algorithms across various scenarios. The scenarios include different game maps and team sizes in StarCraft multi-agent challenge (SMACv2) and Gold Miner, as well as different configurations of the Multi-Particle Environments (MPE). The algorithms compared include behavior cloning (BC), independent inverse Q-learning (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), multi-agent soft Q-Imitation Learning (MASQIL), multi-agent adversarial inverse reinforcement learning (MAAIRL), multi-agent generative adversarial imitation learning (MAGAIL), and the proposed Multi-agent Inverse Factorized Q-learning (MIFQ) algorithm with both deterministic and soft policy versions. The results showcase the performance of each algorithm in terms of win rates and average rewards, providing insights into their relative effectiveness in cooperative multi-agent imitation learning.
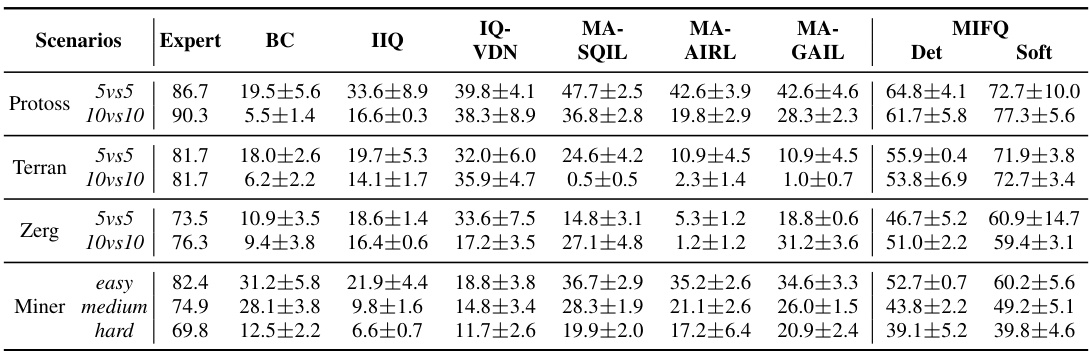
This table presents a comparison of the win rates and rewards achieved by different multi-agent imitation learning algorithms across various scenarios (Protoss, Terran, Zerg) and difficulty levels (easy, medium, hard) in the Gold Miner game, and in the Multi-Particle Environments (MPE). The algorithms are compared against an expert agent’s performance. The results highlight the relative performance of each algorithm in different scenarios.

This table presents a comparison of win rates and rewards achieved by different multi-agent imitation learning (IL) algorithms across various scenarios. The scenarios include different configurations of the StarCraft Multi-Agent Challenge (SMACv2) with varying numbers of agents (5vs5 and 10vs10) and factions (Protoss, Terran, Zerg). In addition, there are three scenarios based on the Gold Miner game (easy, medium, hard) and three Multi-Particle Environments (MPE) (reference, spread, speaker). The algorithms compared include Behavior Cloning (BC), Independent Inverse Q-Learning (IIQ), IQ-Learn with Value Decomposition Network (IQVDN), Multi-Agent Soft Q-Learning (MASQIL), Multi-Agent Adversarial Inverse Reinforcement Learning (MAAIRL), Multi-Agent Generative Adversarial Imitation Learning (MAGAIL), and the proposed method, Multi-agent Inverse Factorized Q-learning (MIFQ). Both deterministic and soft versions of MIFQ are included. The table shows the win rate (percentage) for SMACv2 and Gold Miner games, and reward scores (averaged over runs) for MPE.
Full paper#