↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Many deep learning tasks rely on semi-supervised learning (SSL) to reduce reliance on extensive labeled data. However, a major challenge in SSL is effectively utilizing both labeled and unlabeled data, particularly when annotation budgets are extremely limited. Existing sample selection methods often suffer from shortcomings like imbalanced class distributions or inadequate data coverage, resulting in poor performance. This necessitates more effective sample selection strategies for optimal performance.
To address these limitations, this paper presents RDSS, a novel Representative and Diverse Sample Selection approach. RDSS uses a modified Frank-Wolfe algorithm to minimize a newly proposed criterion, called a-MMD, which balances representativeness and diversity in sample selection. Experimental results demonstrate that RDSS consistently improves the performance of popular SSL frameworks, outperforming existing methods, even under low-budget conditions. This is achieved by selecting a subset of unlabeled data that is both representative of the entire dataset and diverse in its features.
Key Takeaways#
Why does it matter?#
This paper is vital for researchers in semi-supervised learning (SSL) as it tackles the crucial problem of sample selection, particularly under low-budget scenarios. It introduces a novel approach, RDSS, that significantly enhances model performance by strategically selecting representative and diverse samples for annotation. This addresses a major limitation of existing SSL methods and opens exciting avenues for further research into efficient and effective SSL techniques.
Visual Insights#

This figure visualizes the effects of different sample selection strategies on a dataset of dog images. (a) shows a selection focused on representativeness, resulting in redundancy as many similar images are chosen. (b) shows a selection prioritizing diversity, leading to selection of outliers and poor representation of the dataset. (c) illustrates the proposed method (a-MMD), which balances representativeness and diversity resulting in a more comprehensive and accurate sample selection.
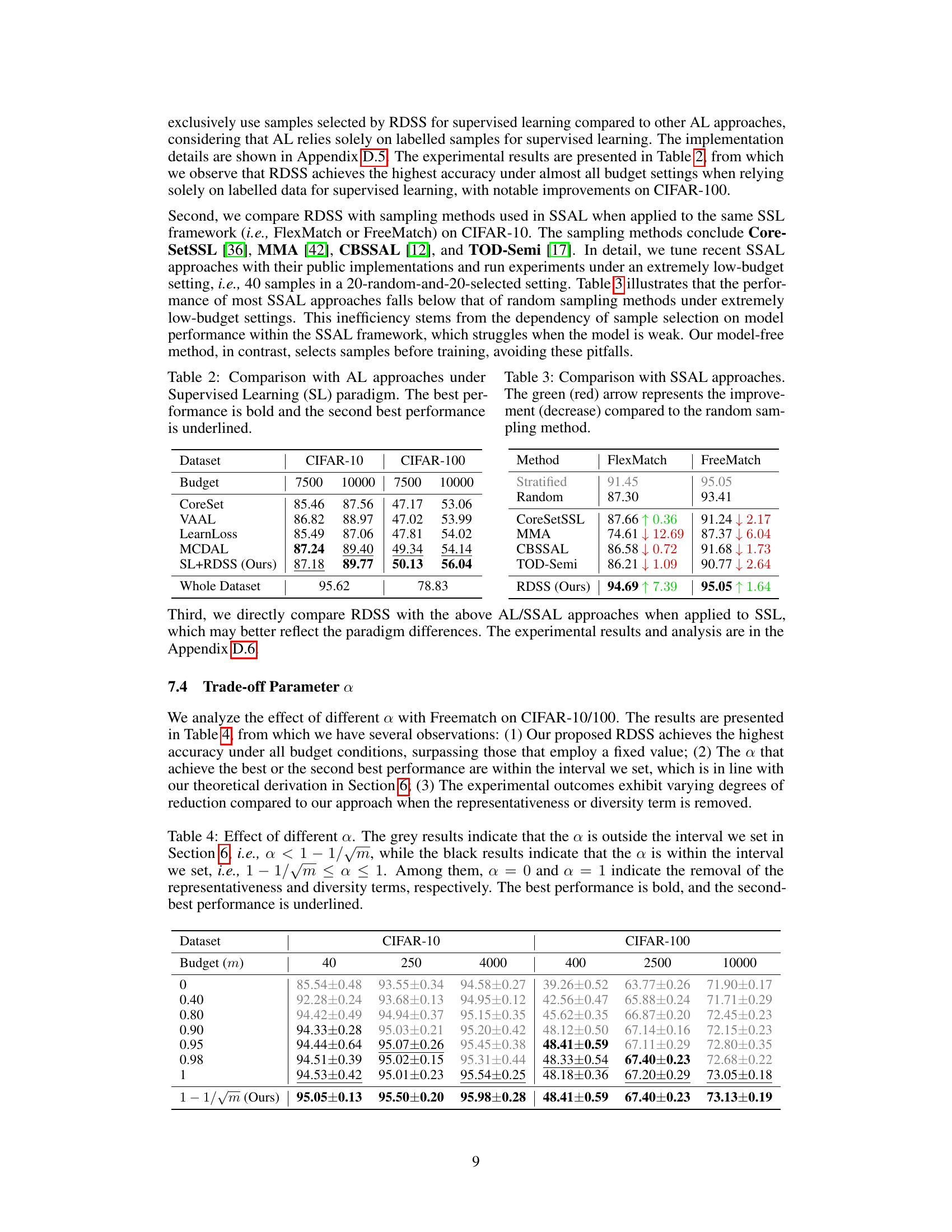
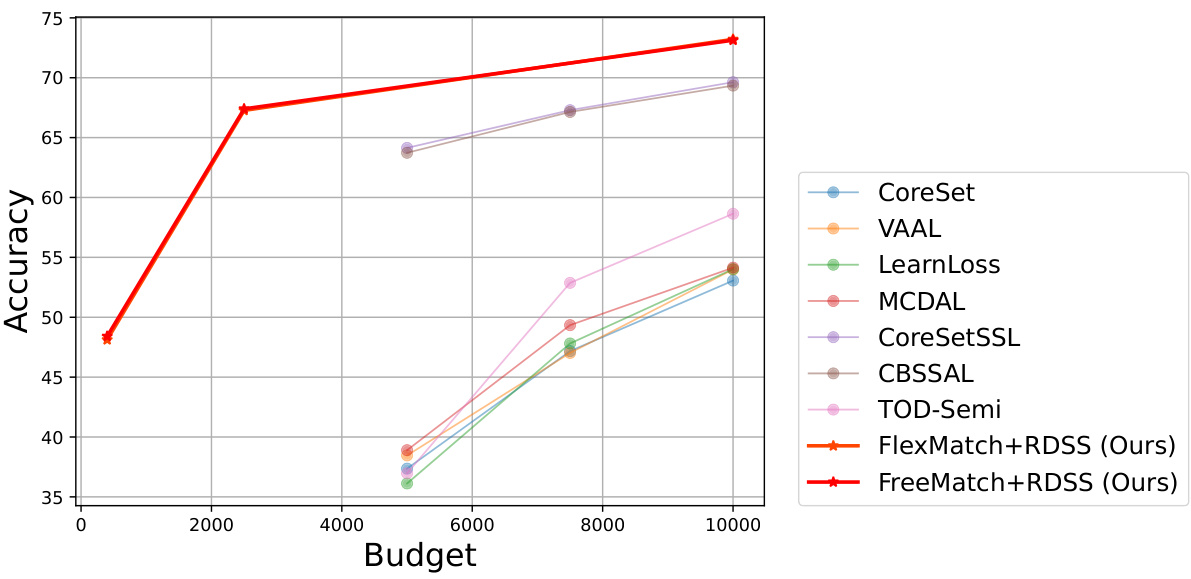
This table compares the performance of RDSS with other sampling methods (Stratified, Random, k-Means, USL, ActiveFT) on multiple datasets (CIFAR-10, CIFAR-100, SVHN, STL-10) and under various annotation budget settings. Results are presented for two different semi-supervised learning frameworks (FlexMatch and FreeMatch). The table highlights RDSS’s superior accuracy and shows that stratified sampling, while theoretically appealing, is impractical in real-world scenarios.
In-depth insights#
RDSS Framework#
The RDSS framework, designed for enhancing semi-supervised learning, centers on a novel sample selection strategy. It cleverly balances representativeness and diversity in selecting a subset of unlabeled data for annotation. The framework leverages a modified Frank-Wolfe algorithm to optimize a new criterion, "a-MMD", which effectively measures the combined aspects of representativeness and diversity. By minimizing a-MMD, RDSS ensures that the selected samples capture the overall data distribution comprehensively while minimizing redundancy. The use of GKHR (Generalized Kernel Herding without Replacement) for optimization makes the approach efficient, especially useful in low-budget scenarios where annotation is expensive. Theoretical guarantees on generalization ability further support the framework’s robustness and efficiency. This is a significant advancement over existing methods that solely focus on one of these characteristics, providing a stronger theoretical foundation and empirically improved performance in the context of semi-supervised learning.
a-MMD Criterion#
The proposed a-MMD criterion is a novel approach to sample selection in semi-supervised learning (SSL), designed to balance representativeness and diversity in the selected subset of unlabeled data. It cleverly modifies the Maximum Mean Discrepancy (MMD) by introducing a trade-off parameter ‘a’. This parameter allows for a controlled adjustment between the emphasis on representativeness and diversity, which is crucial for effective SSL. By minimizing a-MMD, the algorithm aims to select samples that are both representative of the overall data distribution and diverse enough to capture the essential variations within the data. This offers a significant improvement over existing methods which often focus on only one of these aspects. The effectiveness of a-MMD is theoretically supported and empirically demonstrated through experiments, showcasing its ability to improve the generalization ability of SSL models, especially in low-budget settings.
GKHR Algorithm#
The Generalized Kernel Herding without Replacement (GKHR) algorithm is a crucial component of the Representative and Diverse Sample Selection (RDSS) framework. GKHR efficiently solves the optimization problem posed by RDSS, aiming to select a representative and diverse subset of unlabeled data for annotation. It’s a modified version of the Frank-Wolfe algorithm, specifically designed to handle the unique constraints of the a-MMD objective function. The algorithm’s key innovation lies in its ability to avoid selecting repeated samples, which is particularly important under low-budget settings where selecting a diverse representative set is essential. GKHR’s computational complexity is linear with respect to both the number of samples and the size of the selected subset, making it efficient for large datasets. The theoretical analysis of GKHR provides bounds on its optimization error, suggesting that the algorithm converges effectively even with a limited number of iterations. Overall, GKHR’s efficiency and theoretical guarantees make it a vital component of RDSS, enhancing its practical applicability for semi-supervised learning tasks with limited annotation budgets.
Generalization Bounds#
The concept of ‘Generalization Bounds’ in machine learning is crucial for understanding how well a model trained on a finite dataset will perform on unseen data. It establishes a theoretical limit on the difference between a model’s training error and its generalization error (i.e., its performance on new, unseen data). Tight generalization bounds are highly sought after as they provide strong guarantees on a model’s performance, implying that a model’s performance on the training data is a reliable predictor of its performance in the real world. However, deriving such bounds is often challenging and may require strong assumptions about the data distribution and model capacity, making them less practical for many real-world applications. The focus is often on finding bounds that are both informative and achievable, balancing theoretical rigor with practical applicability. Research often involves finding ways to relax assumptions or introduce new techniques that lead to improved bounds, impacting the choice of model architecture, training algorithm, and ultimately the design of machine learning systems.
Future of RDSS#
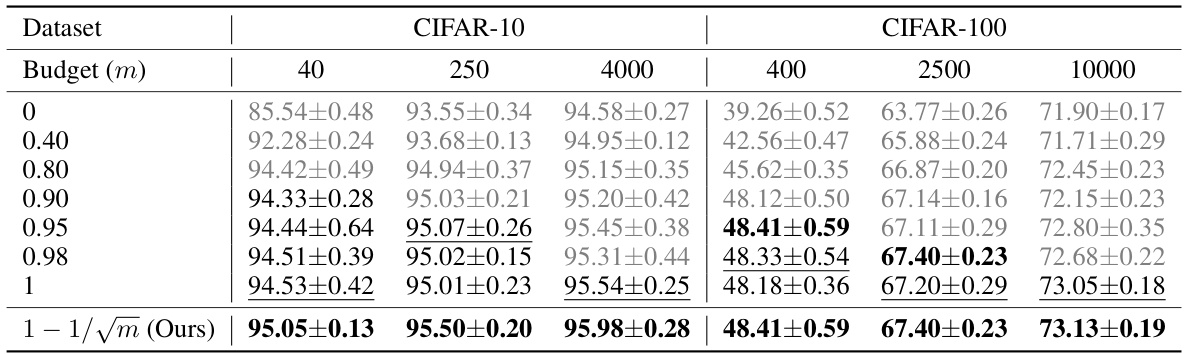
The future of RDSS (Representative and Diverse Sample Selection) looks promising, particularly in addressing the challenges of low-budget semi-supervised learning. Further research could explore adaptive strategies for the trade-off parameter (α) to dynamically balance representativeness and diversity based on data characteristics. Extending RDSS to other data modalities, such as time-series, text, and graph data, would broaden its applicability. Investigating the use of more sophisticated kernel methods or deep learning techniques for sample similarity assessment could enhance RDSS’s performance, potentially allowing it to capture more complex relationships. Finally, focusing on developing more rigorous theoretical guarantees and addressing specific computational efficiency aspects for scaling to massive datasets is crucial for its wider adoption.
More visual insights#
More on figures
This figure visualizes the differences between three sample selection strategies: selecting only representative samples, selecting only diverse samples, and the proposed method (a-MMD). The images show that (a) only selecting representative samples leads to redundancy, (b) only selecting diverse samples leads to an insufficient coverage of the data, and (c) the a-MMD method selects a representative and diverse subset of samples, which is more suitable for semi-supervised learning.

This figure visualizes the effects of different sample selection strategies on a dog dataset. It compares three approaches: selecting samples based only on representativeness (resulting in redundancy), selecting samples based only on diversity (missing much of the data distribution), and the proposed RDSS method which balances representativeness and diversity for optimal coverage and accuracy.
This figure visualizes the effect of different sample selection strategies on a dog dataset. Panel (a) shows a selection focused on representativeness only, resulting in redundancy as many similar samples are chosen. Panel (b) shows a selection prioritizing diversity, which leads to an uneven representation of the dataset. Panel (c) demonstrates the proposed method (a-MMD), effectively balancing representativeness and diversity for a more comprehensive and accurate representation of the dataset.
This figure visualizes the results of three different sample selection strategies on a subset of dog images. (a) shows a selection focused only on representativeness, resulting in redundancy as many similar images are chosen. (b) shows a selection focused only on diversity, leading to an uneven and incomplete representation of the dataset. (c) shows the proposed method (a-MMD), achieving both representativeness and diversity, offering a balanced and comprehensive selection of samples.
More on tables
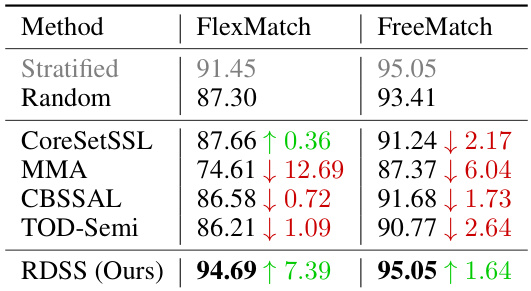
This table compares the performance of RDSS against several other sampling methods (Stratified, Random, k-Means, USL, ActiveFT) across two different semi-supervised learning frameworks (FlexMatch and FreeMatch). The results are presented for different annotation budget settings and across several datasets (CIFAR-10, CIFAR-100, SVHN, STL-10). The table highlights the superior performance of RDSS, especially under low budget conditions.
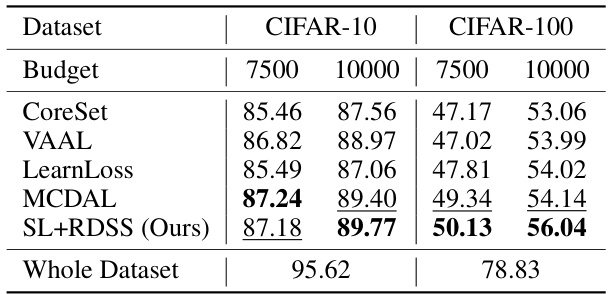
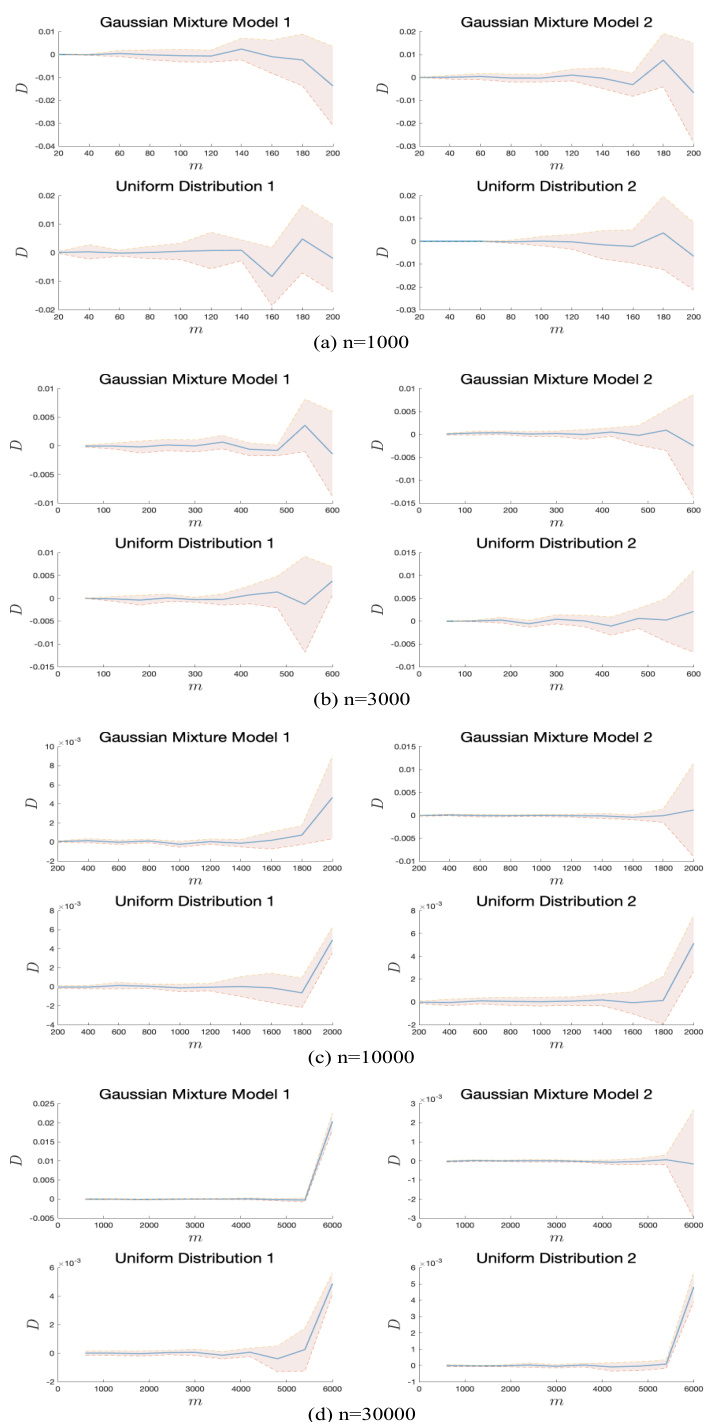
This table compares the performance of the proposed RDSS method against other Active Learning (AL) approaches under the supervised learning setting. The results are shown for both CIFAR-10 and CIFAR-100 datasets, with different annotation budgets. The best and second-best accuracies among all the compared methods (including RDSS) are highlighted. The ‘Whole Dataset’ row shows the performance when using the full dataset for training, providing a context for evaluating the effectiveness of different sample selection techniques.
This table compares the performance of RDSS with other sampling methods (Stratified, Random, k-Means, USL, and ActiveFT) across different annotation budgets on CIFAR-10, CIFAR-100, SVHN, and STL-10 datasets, using both FlexMatch and FreeMatch as SSL frameworks. It highlights RDSS’s superior accuracy, especially under low-budget settings, and demonstrates the limitations of stratified sampling in real-world scenarios.
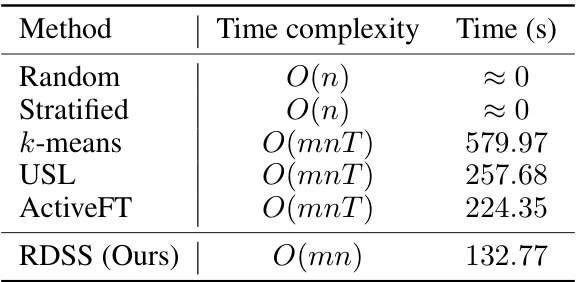
This table compares the performance of different sample selection methods (Random, k-Means, USL, ActiveFT, and RDSS) when integrated with two state-of-the-art semi-supervised learning frameworks (FlexMatch and FreeMatch). The results are presented for various datasets (CIFAR-10, CIFAR-100, SVHN, STL-10) and annotation budgets. The table highlights RDSS’s superior performance across different datasets and budget settings, especially when compared to other methods.
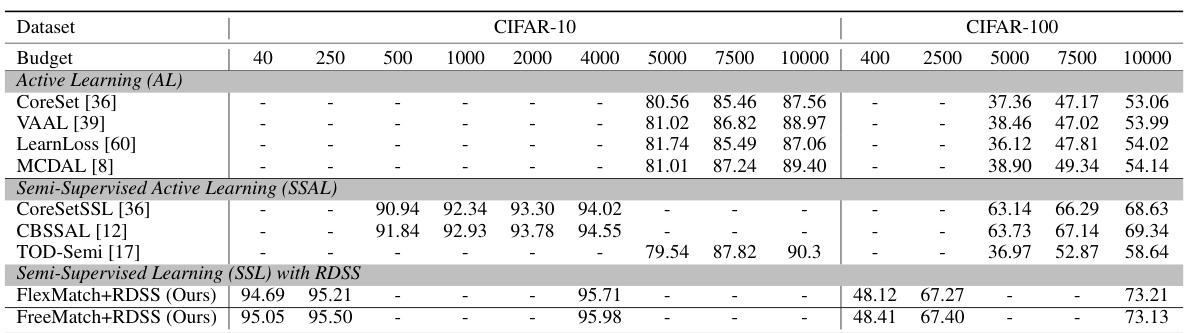
This table compares the performance of the proposed RDSS method with several other sampling methods (Stratified, Random, k-Means, USL [50], and ActiveFT [57]) across different annotation budget settings. The results are shown for two different semi-supervised learning frameworks (FlexMatch and FreeMatch) and multiple datasets. It demonstrates RDSS’s superior performance, especially in low-budget scenarios.
Full paper#