↗ OpenReview ↗ NeurIPS Homepage ↗ Chat
TL;DR#
Softmax computation is a significant bottleneck in many machine learning applications, particularly in high-dimensional settings such as large language models. Existing methods often focus on reducing complexity with respect to the vocabulary size (number of classes), but not the input vector dimension. The high computational cost of softmax becomes more pronounced as models scale up in size and complexity.
This paper introduces AdaptiveSoftmax, a novel algorithm that efficiently computes the top k softmax values by adaptively focusing computational resources on the most important outputs. AdaptiveSoftmax leverages ideas from multi-armed bandit algorithms to improve sample efficiency. The algorithm is supported by theoretical guarantees, demonstrating improvements of up to 30x over full softmax computation. Empirical evaluations on real-world datasets, including the Mistral-7B model on Wikitext, corroborate the significant performance gains.
Key Takeaways#
Why does it matter?#
This paper is highly important for researchers working on large language models and other machine learning applications that heavily use the softmax function. It presents a novel algorithm, AdaptiveSoftmax, that significantly improves the efficiency of softmax computation, especially in high-dimensional settings. This is particularly relevant given the increasing use of LLMs and the computational bottlenecks associated with softmax calculations in such models. The theoretical guarantees and empirical results demonstrate a considerable speedup, opening up new avenues for improving the scalability and performance of LLM inference and training. The proposed methods for efficiently estimating the partition function are also of independent interest.
Visual Insights#
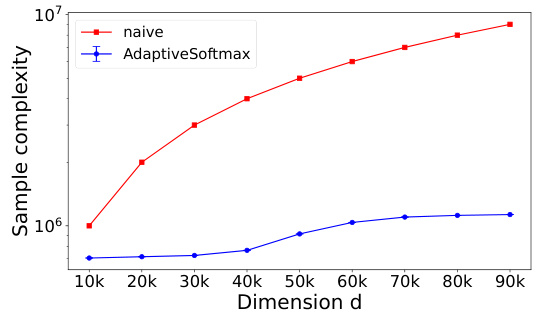
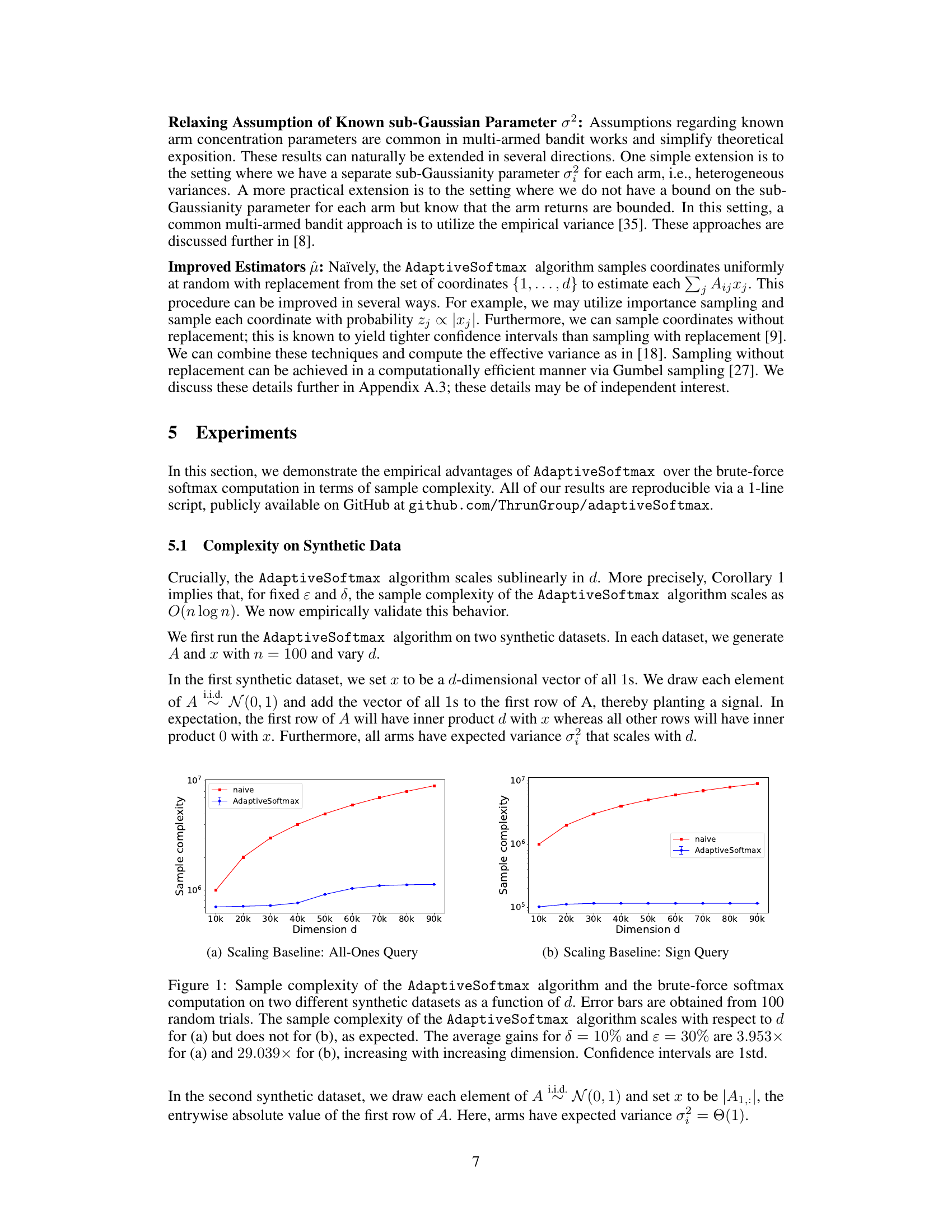
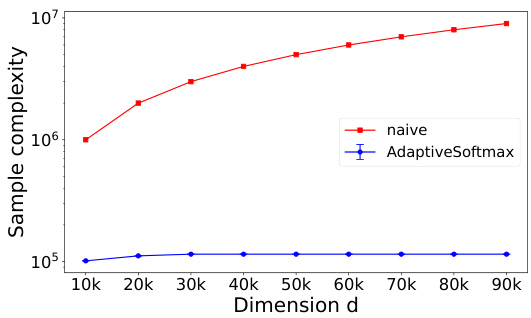
This figure shows the sample complexity of the Adaptive Softmax algorithm and the naive (brute-force) softmax computation on two synthetic datasets, as a function of the dimension (d). The figure demonstrates that Adaptive Softmax has sublinear scaling with d in certain scenarios, significantly outperforming the naive approach. Error bars represent the standard deviation over 100 random trials. The gains from using Adaptive Softmax are shown to increase as the dimension increases.

This table presents the performance gains achieved by the AdaptiveSoftmax algorithm compared to a standard softmax computation for two multiclass classification tasks: EuroSAT and MNIST. The gains are expressed as a multiplicative speedup (e.g., 5.18x means AdaptiveSoftmax is 5.18 times faster). The success rate indicates how often AdaptiveSoftmax correctly identifies the maximum likelihood output and estimates its probability within a specified multiplicative accuracy (30%). The table shows results for different failure probability thresholds (δ = 10%, 5%, 1%).
In-depth insights#
Adaptive Softmax#
Adaptive softmax methods aim to improve the efficiency of softmax computations, particularly in high-dimensional settings common in deep learning. Standard softmax calculations can be computationally expensive due to the need to compute exponentials and normalize over a large number of classes. Adaptive methods address this by focusing computation on the most relevant parts of the softmax, typically by prioritizing high-probability outputs or adaptively sampling classes during training or inference. This adaptivity can involve techniques from multi-armed bandits or importance sampling, aiming to achieve a desirable trade-off between accuracy and computational cost. Theoretical guarantees on the accuracy and sample complexity of such methods are often developed to provide confidence in their performance. Real-world applications often demonstrate significant speedups compared to standard softmax implementations, especially for very large language models. However, challenges remain in terms of balancing adaptivity with computational efficiency and ensuring the robustness of these methods across diverse datasets and model architectures.
PAC Guarantees#
Probably Approximately Correct (PAC) guarantees are a cornerstone of theoretical computer science, offering strong assurances about the performance of algorithms. In the context of machine learning, PAC guarantees provide a probabilistic framework for analyzing the reliability of model predictions. This is particularly valuable when dealing with complex models like those employing softmax functions, where the computational cost of obtaining exact solutions can be prohibitive. AdaptiveSoftmax leverages PAC analysis to provide guarantees on the accuracy of its approximation of the top k softmax outputs. This means that under specified conditions, the algorithm’s estimates will fall within a certain multiplicative error bound with a high probability. The PAC framework allows researchers to rigorously quantify the trade-off between computational efficiency and accuracy. Crucially, the PAC guarantees associated with AdaptiveSoftmax demonstrate a strong theoretical foundation, bolstering confidence in the reliability of the approximation despite the adaptive, statistically driven nature of the algorithm. Understanding the specific parameters (ε and δ) of the PAC guarantee is crucial for interpreting the practical implications. The choice of ε reflects the desired level of accuracy, while δ governs the acceptable probability of the algorithm failing to meet that accuracy level. By carefully selecting these parameters, one can tailor the algorithm’s performance to the needs of specific applications.
Sample Efficiency#
Sample efficiency, in the context of machine learning, refers to the ability of a model to learn effectively from a limited amount of training data. The research paper likely investigates the efficiency of the proposed AdaptiveSoftmax algorithm in terms of the number of samples needed to achieve a certain level of accuracy. A key aspect is comparing the sample complexity of AdaptiveSoftmax to traditional softmax methods, highlighting the potential reduction in data requirements. The analysis probably includes theoretical bounds on sample complexity, accompanied by empirical evaluations demonstrating the algorithm’s performance on various datasets. The results may quantify the improvements in sample efficiency, possibly showing that AdaptiveSoftmax requires significantly fewer samples than standard approaches. Moreover, the discussion likely covers the factors that influence sample efficiency, such as dimensionality, the nature of the dataset, and the desired accuracy level. Probabilistic guarantees on the accuracy of the approximation may also be a significant aspect of the evaluation, indicating the reliability and trustworthiness of results obtained with fewer samples. The overall goal is to showcase how AdaptiveSoftmax achieves comparable or even better performance while using substantially less training data, thus improving resource utilization and potentially reducing costs.
Real-World Tests#
A dedicated ‘Real-World Tests’ section would significantly bolster a research paper on softmax approximation. It should showcase the algorithm’s performance on diverse, complex datasets representative of actual application scenarios. Concrete examples are crucial, such as large language models, image classification systems, or recommendation engines. For each application, the section should clearly state the dataset used, the evaluation metrics (e.g., accuracy, speedup factor, inference time), and a comparison against baseline methods (like a naive softmax implementation). Visualizations such as graphs or tables are essential for presenting the results effectively. Statistical significance should be rigorously addressed to ensure the observed improvements are not due to random chance. Furthermore, the ‘Real-World Tests’ section needs to discuss any practical limitations encountered during implementation. For instance, were there memory constraints, computational bottlenecks, or integration challenges? Addressing these issues adds credibility and practicality to the findings, ultimately showing the algorithm’s true potential for real-world impact.
Future Work#
The ‘Future Work’ section of this research paper on adaptive softmax approximation presents exciting avenues for improvement and expansion. Extending the algorithm to handle top-k selections instead of just the top element is crucial for broader applicability, especially in tasks like nucleus sampling within LLMs. Improving the algorithm’s efficiency in low-dimensional settings is another important goal, potentially through exploring novel techniques to complement its existing strengths in high dimensions. Furthermore, thorough investigation into the trade-off between adaptivity and computational efficiency (wall-clock time) is necessary to maximize the algorithm’s practical impact. Finally, research should explore the combination of adaptive sampling with techniques like LSH (Locality-Sensitive Hashing) to further optimize performance, potentially achieving sub-quadratic complexity. The algorithm’s independence from prior knowledge about data distribution is a key strength that should be further leveraged for more robust and reliable performance in real-world applications. Moreover, its applicability to other problems like kernel density estimation warrants deeper exploration.
More visual insights#
More on figures
This figure shows the sample complexity of AdaptiveSoftmax and the naive softmax computation on two synthetic datasets. Dataset (a) shows that AdaptiveSoftmax scales sublinearly with the dimension (d) of the input, while dataset (b) shows that the sample complexity of AdaptiveSoftmax is largely independent of d. This demonstrates the sublinear scaling of AdaptiveSoftmax in the dimension of the input and its significantly improved efficiency compared to the naive approach.
This figure demonstrates the scaling behavior of the Adaptive Softmax algorithm and a standard softmax computation on two synthetic datasets. The x-axis represents the dimension (d) of the input vector, and the y-axis represents the sample complexity. Two subfigures (a) and (b) show results for different synthetic data generation methods. In (a), the Adaptive Softmax algorithm’s sample complexity scales with d, as expected, while in (b), it does not. Error bars indicate the standard deviation across 100 random trials. The figure highlights the significant gains in sample efficiency achieved by the Adaptive Softmax algorithm, especially in (b), where the gain is larger than 29x.
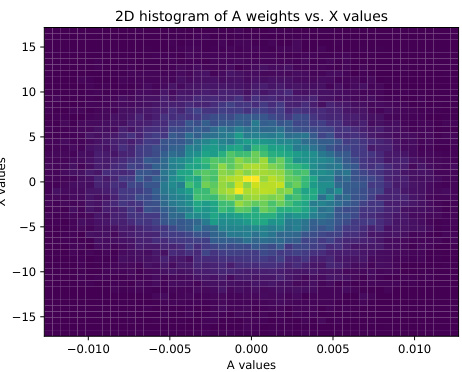
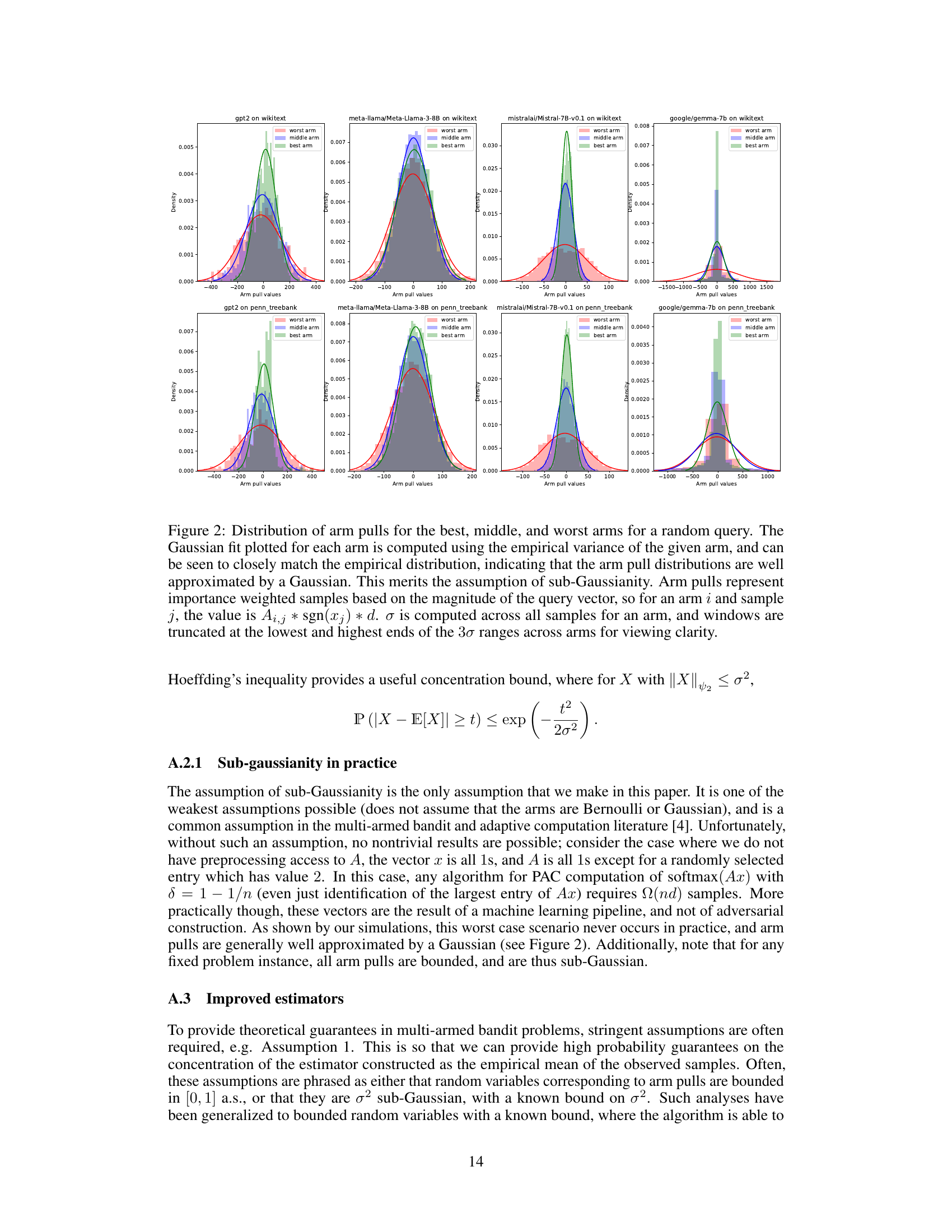
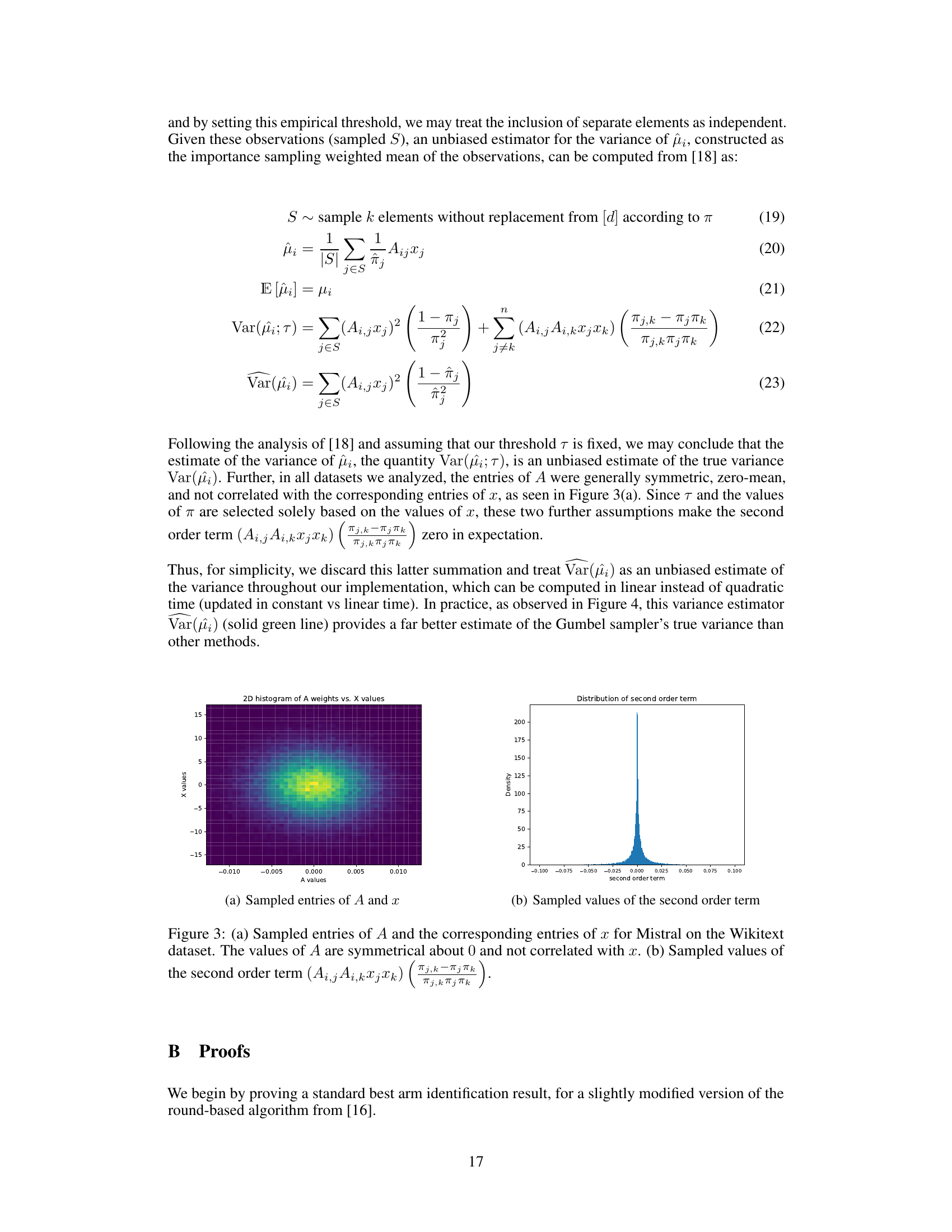
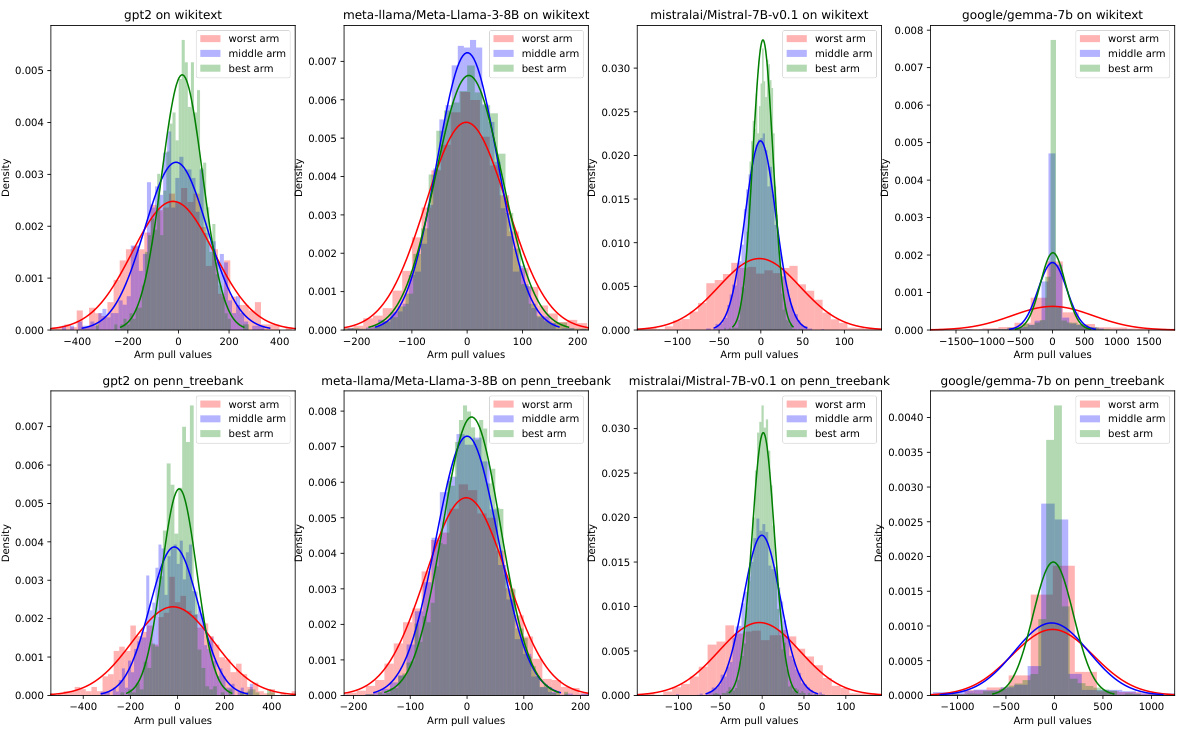
This figure shows the distribution of sampled entries of matrix A and vector x for the Mistral language model on the Wikitext dataset. Panel (a) is a 2D histogram showing a symmetrical distribution centered around zero, indicating no correlation between A and x values. Panel (b) displays a histogram of the second-order term, which is relevant for variance calculations in the AdaptiveSoftmax algorithm.
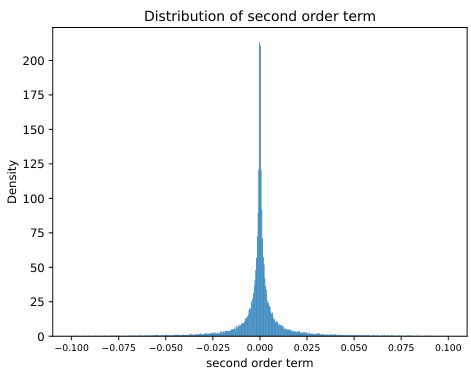
This figure visualizes the properties of the sampled entries of matrix A and vector x in the context of the Mistral model applied to the Wikitext dataset. Panel (a) shows a 2D histogram illustrating the relationship between the sampled values from A and x, revealing a symmetrical distribution around zero and demonstrating a lack of correlation between the two sets of values. Panel (b) presents the distribution of the calculated second-order term, (Ai,j; Ai,kXjXk)(Tj,k - TjTk)/(Tjπk). The distribution of this second-order term is shown to be highly concentrated around zero. These observations support the assumptions made in the theoretical analysis of the paper regarding the statistical properties of the data.
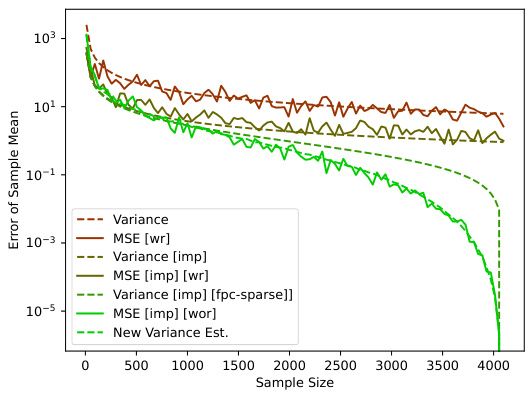
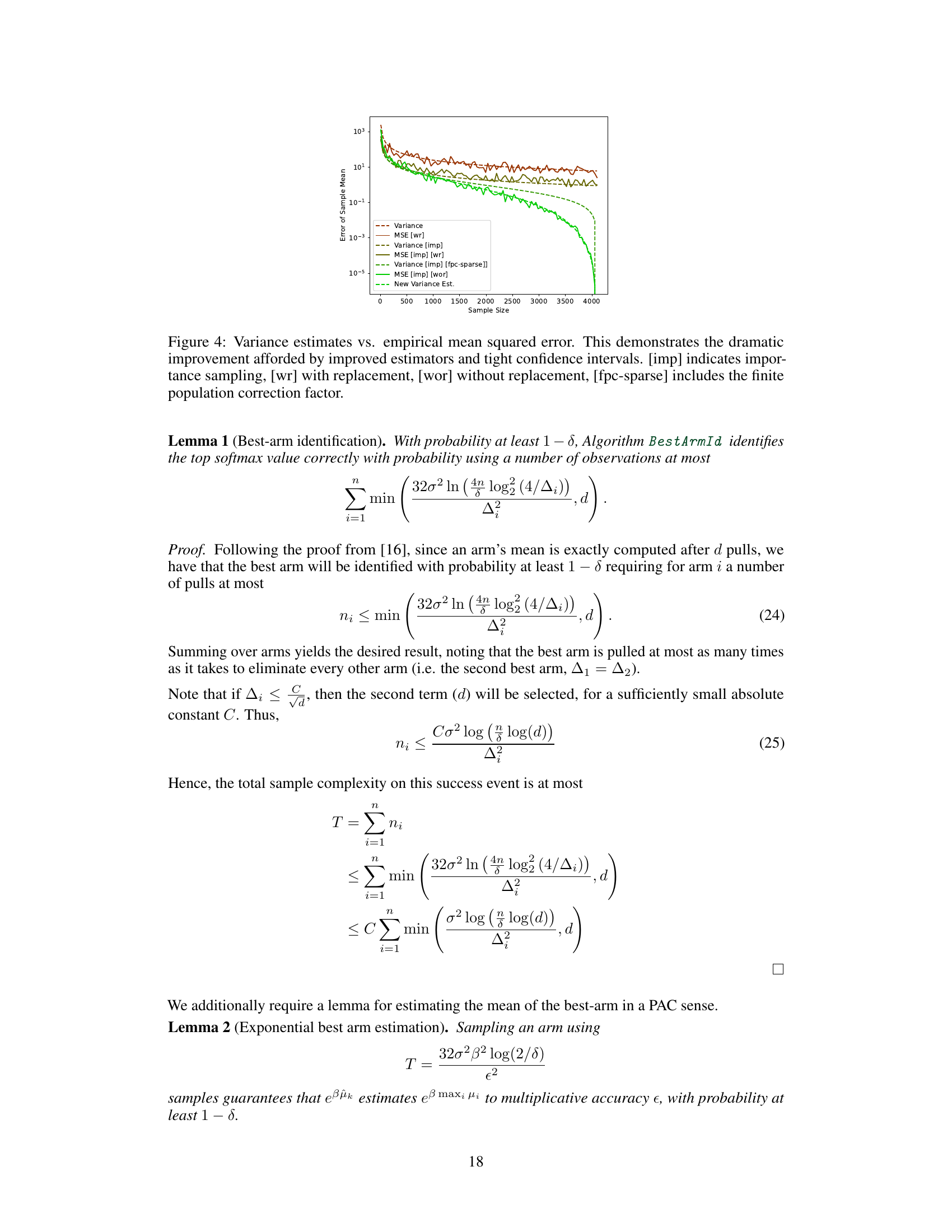
This figure compares different variance estimation methods for the AdaptiveSoftmax algorithm. It shows the mean squared error (MSE) against the sample size. The methods compared include: variance estimation with replacement (wr), variance estimation with importance sampling (imp) with and without replacement, variance estimation with importance sampling and finite population correction (fpc-sparse), and a new variance estimation method proposed in the paper. The results demonstrate that the new method significantly reduces the MSE compared to the existing methods, especially with larger sample sizes.
More on tables

This table presents the performance of AdaptiveSoftmax on various LLMs for the task generation task. For each model and dataset (Wikitext and Penn Treebank), it shows the speedup (in times) achieved by AdaptiveSoftmax compared to a brute-force softmax calculation, along with the success rate (percentage of times the algorithm correctly identifies the maximum likelihood output and estimates its probability within a multiplicative error of 30%). Different δ values (failure probability) are also considered.

This table shows the improvement in sample efficiency and success rate of the AdaptiveSoftmax algorithm compared to the brute-force softmax computation for multinomial logistic regression on two real-world datasets: EuroSAT and MNIST. The success rate indicates the percentage of times the algorithm correctly identified the maximum likelihood output and estimated its probability with a multiplicative accuracy of ε = 30%. The improvement factor is calculated as the ratio of the sample complexity of the brute-force method to that of AdaptiveSoftmax.
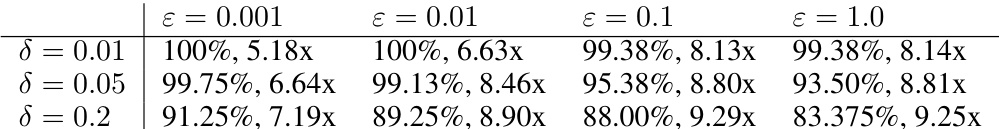
This table presents the performance of the AdaptiveSoftmax algorithm compared to the brute-force softmax computation on two real-world datasets: EuroSAT and MNIST. For each dataset, the table shows the speedup (improvement) achieved by AdaptiveSoftmax in terms of sample complexity, along with its success rate (percentage of times the algorithm correctly identifies the highest probability output and estimates its value with a multiplicative error of less than 30%). The success rate is calculated using 800 test queries for each dataset.
Full paper#